Сложение чисел с корнями: Сложение и вычитание квадратных корней: определение, примеры, правила

Содержание

Сложение и вычитание квадратных корней: определение, примеры, правила

Извлечение квадрантного корня из числа не единственная операция, которую можно производить с этим математическим явлением. Так же как и обычные числа, квадратные корни складывают и вычитают.

Правила сложения и вычитания квадратных корней

Определение 1

Такие действия, как сложение и вычитание квадратного корня, возможны только при условии одинакового подкоренного выражения.

Пример 1

Можно сложить или вычесть выражения 23 и 63, но не 56 и 94. Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.

Действия с корнями: основы

Пример 2

650-28+512

Алгоритм действия:

Упростить подкоренное выражение. Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня. Обращаем ваше внимание, что второй множитель заносится под знак корня.
После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!

Совет 1

Если у вас пример с большим количеством одинаковых подкоренных выражений, то подчеркивайте такие выражения одинарными, двойными и тройными линиями, чтобы облегчить процесс вычисления.

Пример 3

Давайте попробуем решить данный пример:

650=6(25×2)=(6×5)2=302. Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 302.

28=2(4×2)=(2×2)2=42. Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 42.

512=5(4×3)=(5×2)3=103. Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 103.

Результат упрощения: 302-42+103

302-42+103=(30-4)2+103=262+103.

В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.

Пример 4

(45)+45:

Упрощаем (45). Раскладываем 45 на множители: (45)=(9×5);
Выносим 3 из-под корня (9=3):45=35;
Складываем множители у корней: 35+45=75.

Пример 5

640-310+5:

Упрощаем 640. Раскладываем 40 на множители: 640=6(4×10);
Выносим 2 из-под корня (4=2):640=6(4×10)=(6×2)10;
Перемножаем множители, которые стоят перед корнем: 1210;

Записываем выражение в упрощенном виде: 1210-310+5;
Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: (12-3)10=910+5.

Пример 6

95-23-45

Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.д.) и записываем результат:

(9-4)5-23=55-23.

Советы:

Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.
Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
Не следует суммировать или вычитать целое число или корень: 3+(2x)1/2.
При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Навигация по статьям

Предыдущая статья

Ранг матрицы

Следующая статья

Деление корней

Арифметические корни натуральной степени
Деление корней
Извлечение корней
Комплексные числа
Разложение квадратного корня на множители: методы
Все темы по математике

Дипломные работы
Курсовые работы
Рефераты
Контрольные работы
Отчет по практике

Эссе

Узнать подробнее

Актуальность строительства

Вид работы:
Реферат
Выполнена:
17 января 2023 г.
Стоимость:
1 400 руб

Заказать такую же работу

контрольная номер один вариант один

Вид работы:

Контрольная работа
Выполнена:
7 декабря 2022 г.
Стоимость:
800 руб

Заказать такую же работу

Расширение числовых множеств

Заказать такую же работу

Решить с объяснением

Вид работы:
Решение задач
Выполнена:
20 ноября 2022 г.
Стоимость:
800 руб

Заказать такую же работу

дифференциальные уравнения

Вид работы:
Домашняя работа
Выполнена:
26 октября 2022 г.
Стоимость:
800 руб

Заказать такую же работу

Изложены в приложенных файлах

Вид работы:
Практическая работа
Выполнена:
25 октября 2022 г.
Стоимость:
3 000 руб

Заказать такую же работу

Смотреть все работы по строительству

Сложение корней, вычитание корней с одинаковыми и разными показателями

Определение

Действие сложения и вычитания квадратных корней возможно лишь при условии одинаковости подкоренных выражений слагаемых.

Сложение корней, формулы

Складывать подобные квадратные корни, то есть иррациональные выражения с одинаковым основанием, очень просто. Для этого суммируют множители слагаемых, а подкоренное число остается неизменным:

\(m\sqrt a+n\sqrt a=\left(m+n\right)\sqrt a\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В случае со сложением корней с разными подкоренными значениями нужно привести их к подобию. Упрощение корневых чисел выполняют по следующему алгоритму:

Раскладывание подкоренного числа на два множителя так, чтобы один из них являлся числом, из которого извлекается целый квадратный корень.
Извлечение корня из квадратного числа, запись ответа перед символом корня. Второй множитель остается под знаком корня.
Упрощенные корни с одинаковым основанием можно складывать как подобные.

Пример

\(3\sqrt{50}+2\sqrt8+\sqrt{12}\)

\(3\sqrt{50}=3\sqrt{25\times2}=3\times5\sqrt2=15\sqrt2\)

\(2\sqrt8=2\sqrt{4\times2}=2\times2\sqrt2=4\sqrt2\)

\(\sqrt{12}\;=\sqrt{4\times3}=2\times1\sqrt2=2\sqrt2\)

После упрощения исходное выражение приобретает вид:

\(15\sqrt2+4\sqrt2+2\sqrt2=21\sqrt2\)

Примечание

Подкоренные выражения между собой не суммируются и не вычитаются. При этом выражения под одним корнем складываются и вычитаются как обычные числа.

Вычитание корней, формулы

При вычитании подобных корней вычитаются их множители, а подкоренное выражение не меняется:

\(m\sqrt a-n\sqrt a=\left(m-n\right)\sqrt a\)

Чтобы узнать разность иррациональных чисел с разным основанием, нужно привести уменьшаемое и вычитаемое к единому образцу. Для этого используют тот же алгоритм, что и перед сложением.

Пример

\(4\sqrt{75}-3\sqrt{24}\)

\(4\sqrt{75}=4\sqrt{25\times3}=4\times5\sqrt3=20\sqrt3\)

\(3\sqrt{12}=3\sqrt{4\times3}=3\times2\sqrt3=6\sqrt3\)

Упростив, получаем:

\(20\sqrt3-6\sqrt3=14\sqrt3\)

Сложение корней со степенями

Складывание и вычитание корней с разными степенями, но одинаковым основанием имеет следующую последовательность:

Допустим, надо решить данное выражение:

\(\sqrt[3]а+\sqrt[4]а\)

Для начала проведем процедуру упрощения:

\(\sqrt[3]а+\sqrt[4]а=12\times\sqrt a^4+12\times\sqrt a^3\)

\(12\times\sqrt a^4+12\times\sqrt a^3=12\times\sqrt{a^4+a^3}\)

При приведении двух подобных членов к общему показателю корневого числа применяется одно из свойств корней. 2}=\left|а-2\right|+\left|а-4\right|\)

Раскроем модули в промежутке \(2\leq а\leq4\):

\(\vert а-2\vert=а-2,\;т.к.\;а-2\geq0\)

\(\vert а-4\vert=4-а,\;т.к.\;а-4\leq0\)

Следовательно, \(\vert а-2\vert+\vert а-4\vert=а-2+4-а=2\)

Ответ: 2.

9.3 Сложение и вычитание квадратных корней — Элементарная алгебра 2e

Цели обучения

К концу этого раздела вы сможете:

Сложение и вычитание как квадратный корень
Сложение и вычитание квадратных корней, требующих упрощения

Будь готов 9,7

Прежде чем начать, пройдите этот тест на готовность.

Добавить: ⓐ 3x+9x3x+9x ⓑ 5м+5н5м+5н.
Если вы пропустили эту проблему, просмотрите пример 1.24.

Будь готов 9,8

Упрощение: 50x350x3.
Если вы пропустили эту проблему, просмотрите пример 9.16.

Мы знаем, что должны соблюдать порядок операций для упрощения выражений с квадратными корнями. Радикал — это группирующий символ, поэтому сначала мы работаем внутри радикала. Мы упрощаем 2+72+7 следующим образом:

2+7Добавить внутри корня.9Упростить.32+7Добавить внутри корня.9Упростить.3

Итак, если нам нужно добавить 2+72+7, мы не должны объединять их в один радикал.

2+7≠2+72+7≠2+7

Пытаться складывать квадратные корни с разными подкоренными, это все равно, что пытаться складывать разные члены.

Но так же, как мы можем сложить x+x, мы можем сложить 3+3.x+x=2×3+3=23Но так же, как мы можем сложить x+x, мы можем сложить 3+3.x+x=2×3+3= 23

Сложение квадратных корней с одним и тем же основанием аналогично сложению одинаковых членов. Мы называем квадратные корни теми же подкоренными, что и квадратные корни, чтобы напомнить нам, что они работают так же, как и термины.

Как квадратные корни

Квадратные корни с одинаковыми подкоренными называются квадратными корнями.

Мы складываем и вычитаем квадратные корни точно так же, как слагаем и вычитаем одинаковые члены. Мы знаем, что 3x+8x3x+8x равно 11x11x. Точно так же мы добавляем 3x+8x3x+8x, и в результате получается 11x.11x.

Сложение и вычитание как квадратный корень

Подумайте о добавлении похожих терминов с переменными, как в следующих нескольких примерах. Когда у вас есть подкоренные числа, вы просто добавляете или вычитаете коэффициенты. Когда подкоренные не похожи, вы не можете комбинировать термины.

Пример 9.29

Упрощение: 22-7222-72.

Решение

	22-7222-72
Так как радикалы одинаковые, вычитаем коэффициенты.	−52−52

Попробуй 9,57

Упрощение: 82−9282−92.

Попробуй 9,58

Упрощение: 53−9353−93.

Пример 9.30

Упрощение: 3г+4г3г+4г.

Решение

	3г+4г3г+4г
Так как радикалы похожи, складываем коэффициенты.	7 лет 7 лет

Попробуй 9,59

Упрощение: 2x+7x2x+7x.

Попробуй 9,60

Упрощение: 5u+3u5u+3u.

Пример 9.31

Упрощение: 4x−2y4x−2y.

Решение

	4x-2y4x-2y
Так как радикалы не похожи, мы не можем их вычесть. Оставляем выражение как есть.	4x−2y4x−2y

Попробуй 9,61

Упрощение: 7p-6q7p-6q.

Попробуй 9,62

Упрощение: 6a−3b6a−3b.

Пример 9.32

Упрощение: 513+413+213513+413+213.

Решение

	513+413+213513+413+213
Так как радикалы похожи, складываем коэффициенты.	11131113

Попробуй 9,63

Упрощение: 411+211+311411+211+311.

Попробуй 9,64

Упрощение: 610+210+310610+210+310.

Пример 9.33

Упрощение: 26−66+3326−66+33.

Решение

	26−66+3326−66+33
Поскольку первые два радикала одинаковы, мы вычитаем их коэффициенты.	−46+33−46+33

Попробуй 9,65

Упрощение: 55−45+2655−45+26.

Попробуй 9,66

Упрощение: 37−87+2537−87+25.

Пример 9.34

Упрощение: 25n−65n+45n25n−65n+45n.

Решение

2″ data-label=»»>

	25н-65н+45н25н-65н+45н
Так как радикалы похожи, мы их объединяем.	05н05н
Упрощение.	0

Попробуй 9,67

Упрощение: 7x−77x+47x7x−77x+47x.

Попробуй 9,68

Упрощение: 43г-73г+23г43г-73г+23г.

Когда радикалы содержат более одной переменной, если все переменные и их показатели одинаковы, радикалы подобны.

Пример 9.35

Упрощение: 3xy+53xy-43xy3xy+53xy-43xy.

Решение

	3xy+53xy-43xy3xy+53xy-43xy
Так как радикалы похожи, мы их объединяем.	23xy23xy

Попробуй 9,69

Упрощение: 5xy+45xy-75xy5xy+45xy-75xy.

Попробуй 9,70

Упрощение: 37мин+7мин-47мин37мин+7мин-47мин.

Сложение и вычитание квадратных корней, требующих упрощения

Помните, что мы всегда упрощаем квадратные корни, удаляя наибольший множитель идеального квадрата. Иногда, когда нам нужно сложить или вычесть квадратные корни, которые, как кажется, не имеют одинаковых радикалов, мы находим похожие радикалы после упрощения квадратных корней.

Пример 9,36

Упрощение: 20+3520+35.

Решение

	20+3520+35
По возможности упрощайте радикалы.	4·5+354·5+35
	25+3525+35
Объедините одинаковые радикалы.	5555

Попробуй 9,71

Упрощение: 18+6218+62.

Попробуй 9,72

Упрощение: 27+4327+43.

Пример 9.37

Упрощение: 48−7548−75.

Решение

	48-7548-75
Упростите радикалы.	16·3−25·316·3−25·3
	43-5343-53
Объедините одинаковые радикалы.	−3−3

Попробуй 9,73

Упрощение: 32−1832−18.

Попробуй 9,74

Упрощение: 20−4520−45.

Точно так же, как мы используем ассоциативное свойство умножения, чтобы упростить 5(3x)5(3x) и получить 15x15x, мы можем упростить 5(3x)5(3x) и получить 15x15x. Мы будем использовать ассоциативное свойство, чтобы сделать это в следующем примере.

Пример 9,38

Упрощение: 518−28518−28.

Решение

	518-28518-28
Упростите радикалы.	5·9·2−2·4·25·9·2−2·4·2
	5·3·2−2·2·25·3·2−2·2·2
	152−42152−42
Объедините одинаковые радикалы.	112112

Попробуй 90,75

Упрощение: 427−312427−312.

Попробуй 9,76

Упрощение: 320-745320-745.

Пример 9.39

Упрощение: 34192−5610834192−56108.

Решение

	34192−5610834192−56108
Упростите радикалы.	3464·3−5636·33464·3−5636·3
	34·8·3−56·6·334·8·3−56·6·3
	63−5363−53
Объедините одинаковые радикалы.	33

Попробуй 9,77

Упрощение: 23108−5714723108−57147.

Попробуй 9,78

Упрощение: 35200−3412835200−34128.

Пример 9.40

Упрощение: 2348−34122348−3412.

Решение

	2348−34122348−3412
Упростите радикалы.	2316·3−344·32316·3−344·3
	23·4·3−34·2·323·4·3−34·2·3
	833−323833−323
Найдите общий знаменатель, чтобы вычесть коэффициентов одинаковых радикалов.	1663−9631663−963
Упрощение.	763763

Попробуй 9,79

Упрощение: 2532−1382532−138.

Попробуй 9,80

Упрощение: 1380−141251380−14125.

В следующем примере мы удалим из квадратных корней постоянные и переменные множители.

Пример 9.41

Упрощение: 18n5−32n518n5−32n5.

Решение

	18n5−32n518n5−32n5
Упростите радикалы.	9n4·2n−16n4·2n9n4·2n−16n4·2n
	3n22n−4n22n3n22n−4n22n
Объедините одинаковые радикалы.	−n22n−n22n

Попробуй 9,81

Упрощение: 32м7-50м732м7-50м7.

Попробуй 9,82

Упрощение: 27p3−48p327p3−48p3.

Пример 9.42

Упрощение: 950м2-648м2950м2-648м2.

Решение

	950м2-648м2950м2-648м2
Упростите радикалы.	925м2·2-616м2·3925м2·2-616м2·3
	9·5м·2-6·4м·39·5м·2-6·4м·3
	45м2-24м345м2-24м3
Радикалы не похожи и поэтому не могут быть объединены.

Попробуй 9,83

Упрощение: 532×2−348x2532x2−348×2.

Попробуй 9,84

Упрощение: 748y2−472y2748y2−472y2.

Пример 9.43

Упрощение: 28×2−5×32+518x228x2−5×32+518×2.

Решение

	28×2−5×32+518x228x2−5×32+518×2
Упростите радикалы.	24×2·2−5×16·2+59×2·224×2·2−5×16·2+59×2·2
	2·2x·2-5x·4·2+5·3x·22·2x·2-5x·4·2+5·3x·2
	4×2-20×2+15x24x2-20×2+15×2
Объедините одинаковые радикалы.	−x2−x2

Попробуй 9,85

Упрощение: 312×2−2×48+427x2312x2−2×48+427×2.

Попробуй 9,86

Упрощение: 318×2−6×32+250x2318x2−6×32+250×2.

СМИ

Получите доступ к этому онлайн-ресурсу, чтобы получить дополнительные инструкции и попрактиковаться в сложении и вычитании квадратных корней.

Сложение/вычитание квадратных корней

Раздел 9.3 Упражнения

Практика делает совершенным

Сложение и вычитание как квадратный корень

В следующих упражнениях упрощайте.

145.

82−5282−52

146.

72−3272−32

147.

35+6535+65

148.

45+8545+85

149.

97−10797−107

150.

117−127117−127

151.

7г+2г7г+2г

152.

9н+3н9н+3н

153.

а-4аа-4а

154.

б-6бб-6б

155.

5с+2с5с+2с

156.

7д+2д7д+2д

157.

8а-2б8а-2б

158.

5c-3d5c-3d

159.

5м+н5м+н

160.

н+3пн+3п

161.

87+27+3787+27+37

162.

65+35+565+35+5

163.

311+211−811311+211−811

164.

215+515−915215+515−915

165.

33−83+7533−83+75

166.

57−87+6357−87+63

167.

62+22−3562+22−35

168.

75+5−81075+5−810

169.

32а-42а+52а32а-42а+52а

170.

11б-511б+311б11б-511б+311б

171.

83с+23с-93с83с+23с-93с

172.

35д+85д-115д35д+85д-115д

173.

53аб+3аб-23аб53аб+3аб-23аб

174.

811кд+511кд-911кд811кд+511кд-911кд

175.

2pq-5pq+4pq2pq-5pq+4pq

176.

112рс-92рс+32рс112рс-92рс+32рс

Сложение и вычитание квадратных корней, требующих упрощения

В следующих упражнениях упрощайте.

177.

50+4250+42

178.

48+2348+23

179.

80−3580−35

180.

28−4728−47

181.

27−7527−75

182.

72−9872−98

183.

48+2748+27

184.

45+8045+80

185.

250−372250−372

186.

398−128398−128

187.

212+348212+348

188.

475+2108475+2108

189.

2372+15502372+1550

190.

2575+34482575+3448

191.

1220−23451220−2345

192.

2354−34962354−3496

193.

1627−38481627−3848

194.

1832−110501832−11050

195.

1498−131281498−13128

196.

1324+14541324+1454

197.

72a5−50a572a5−50a5

198.

48b5−75b548b5−75b5

199.

80c7−20c780c7−20c7

200.

96d9−24d996d9−24d9

201.

980p4-698p4980p4-698p4

202.

872q6-375q6872q6-375q6

203.

250р8+454р8250р8+454р8

204.

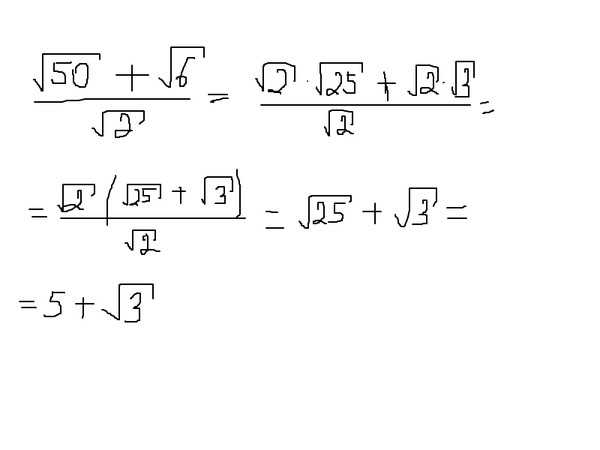
527с6+220с6527с6+220с6

205.

320×2−445×2+5x80320x2−445×2+5×80

206.

228×2-63×2+6x7228x2-63×2+6×7

207.

3128y2+4y162−898y23128y2+4y162−898y2

208.

375y2+8y48−300y2375y2+8y48−300y2

Смешанная практика

209.

28+68−5828+68−58

210.

2327+34482327+3448

211.

175k4−63k4175k4−63k4

212.

56162+31612856162+316128

213.

2363−23002363−2300

214.

150+46150+46

215.

92−8292−82

216.

5x−8y5x−8y

217.

813−413−313813−413−313

218.

512c4-327c6512c4-327c6

219.

80a5−45a580a5−45a5

220.

3575−14483575−1448

221.

2119−2192119−219

222.

500+405500+405

223.

5627+58485627+5848

224.

1111−10111111−1011

225.

75−10875−108

226.

298−472298−472

227.

424×2-54×2+3x6424x2-54×2+3×6

228.

880y6−648y6880y6−648y6

Математика на каждый день

229.

Художник-декоратор решил использовать квадратную плитку в качестве акцентной полосы в дизайне новой душевой, но она хочет повернуть плитку так, чтобы она выглядела как ромб. Она возьмет 9 больших плиток со стороной 8 дюймов и 8 маленьких плиток со стороной 2 дюйма. Определим ширину акцентной полосы, упростив выражение 9(82)+8(22)9(82)+8(22). (Округлить до десятых долей дюйма.)

230.

Сьюзи хочет использовать квадратную плитку на границе спа-салона, который она устанавливает на заднем дворе. Она будет использовать большие плитки площадью 12 квадратных дюймов, средние плитки площадью 8 квадратных дюймов и маленькие плитки площадью 4 квадратных дюйма. Для одного участка границы потребуется 4 большие плитки, 8 средних плиток и 10 маленьких плиток, чтобы покрыть ширину стены. Упростите выражение 412+88+104412+88+104, чтобы определить ширину стены. (Округлить до десятых долей дюйма.)

Письменные упражнения

231.

Объясните разницу между подобными радикалами и непохожими радикалами. Убедитесь, что ваш ответ имеет смысл для радикалов, содержащих как числа, так и переменные.

232.

Объясните процесс определения того, являются ли два радикала одинаковыми или разными. Убедитесь, что ваш ответ имеет смысл для радикалов, содержащих как числа, так и переменные.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.

ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?

Как складывать и вычитать из квадратных корней?

квадратный корень из любого числа — это значение, которое дает исходное число при умножении на себя. Квадратный корень и квадрат являются обратными операциями. Например, если число «m» — это квадратный корень из числа «n» (m = √n), то «n» — это квадрат числа «m» (n = m × m). Мы знаем, что квадрат любого числа всегда положителен, поэтому каждое число имеет два квадратных корня, один из которых является положительным значением, а другой — отрицательным. Например, значение квадратного корня из 9равно 3 и -3. Квадратный корень из 9 обозначается как √9, где 9 называется радикалом, а «√» называется подкоренным символом. Квадратный корень из положительного числа x можно записать как (x) ^1/2 , где 1/2 — показатель степени. Теперь, что касается сложения и вычитания квадратных корней, мы можем выполнять операции так же, как и с обычными числами. Но помните, что мы можем складывать или вычитать только квадратные корни или радикалы, у которых одинаковые подкоренные числа. В этой статье давайте подробно узнаем о сложении и вычитании квадратных корней.

Квадратный корень из целого числа x

Как складывать и вычитать радикалы?

Как мы обсуждали выше, мы можем складывать или вычитать только квадратные корни или радикалы, которые имеют одинаковые подкоренные. Если два члена имеют одинаковые подкоренные числа, то мы можем сложить или вычесть их коэффициенты и оставить подкоренные числа как есть. Термины, имеющие одинаковые подкоренные, известны как «подобные радикалы», тогда как термины, имеющие разные подкоренные, известны как «непохожие радикалы».

Во-первых, упростите данные квадратные корни, если это возможно. Итак, попробуйте разложить их на множители, чтобы найти хотя бы один совершенный квадратный множитель.
Как только вы упростите данные квадратные корни членов, найдите такие же радикалы.
Наконец, добавьте или вычтите коэффициенты одинаковых радикалов и оставьте любые дополнительные члены как часть уравнения.

Пример: Решите 8√9 + 3√16.

Решение:

Данное выражение равно 8√9 + 3√16
Здесь оба подкоренных числа различны. Но мы можем упростить их еще больше.
8√9 + 3√16 = 8√(3 ² ) + 3√(4 ² )
= 8 × 3 + 3 × 4
= 24 + 12 = 36.
Таким образом, 8√9 + 3√4
8 Также проверьте
Алгебраические выражения
Типы алгебраических выражений
Решаемые примеры
Пример 1: Упростить: 5√8 + 3√32.
Решение:
Дано выражение: 5√8 + 3√32
Теперь, упрощая радикалы, получаем
5√(2×2×2) + 3√(2×2 ⁴ )
= 5×2√2 + 3×2 ² √2
= 10√2 + 12√52
= 22√2
Следовательно, 5√8 + 3√32 = 22√2.
Пример 2: Упростите 14√3 − 2√12.
Решение:
Полученное выражение: 14√3 − 2√12
×3)
= 14√3 − 2 ×2√3
= 14√3 − 4√3
= 10√3
Следовательно, 14√3 − 2√12 = 10√3.
Пример 3: Решите: 7√(a ²) − 2√(a ⁴) + √(a ²).
Решение:
Указано. 7a − 2a ² + a
= 8a − 2a ²
Таким образом, 7√(a ² ) — 2√(а ⁴ ) + √(а ² ) = 8а — 2а ² .
Пример 4: Решите: 51√7 + 16√5 − 13√7 + 31√5.
Решение:
Данное выражение: 51√7 + 16√5 − 13√7 + 31√5
= (51√7 − 13√7) + (16√5 + 31√5)
= 38√7 + 47√5
Таким образом, 51√7 + 16√5 − 13√7 + 31√5 = 38√7 + 47√5.
Пример 5: Решите: 19√75 + 12√27 − 10√48.
Решение:
Данное выражение: 19√75 + 12√27 − 10√48
= 19√(3×5×5) + 12√(3×3×3) − 10√(4×4×3)
= 19 × 5√3 + 12 × 3√3 − 10 × 4√3
= 95√3 + 36√3 − 40√3
= 91√3
Таким образом, 19√75 + 12√27 − 10√48 = 91√3.
Пример 6: Упростить: 2√3 + 3√3.
Решение:
Дано выражение: 2√3 + 3√3
Теперь, упрощая радикалы, получаем
= 2√3 + 3√3
= 5√3
Следовательно, 2√3 + 3√3 = 5√3
Пример 7: Упрощение: √9 + √25.
Решение:
Учитывая выражение: √9 + √25
Сейчас, упрощающие радикалы, мы получаем
= √9 + √25
= 3 + 5
= 8
, rence, a 9 + √25 = 8
Пример 8. Упростить: √8 + 2√2
Решение:
Данное выражение: √8 + 2√2
0005
= √8 + 2√2
= 2√2 + 2√2 ( Так как √8 = 2√2 )
= 4√2
Следовательно, √8 + 2√5 √2 = 40√0
Пример 9: Упростить: √3×(4√3 + 11 )
Решение:
Данное выражение: √3×(4√3 + 11 )
Теперь, упрощая радикалы 90,5
= √3×(4√3 + 11 )
= √3×4√3 + 11×√3
= 4×3 + 11×√3
= 12 + 11×√3
4 Пример 10: Упростить: √5×(√5 + √6)
Решение:
Полученное выражение: √5×(√5 + √6)
×√5 + √5×√6
= 25 + √30
Часто задаваемые вопросы о квадратных корнях
Вопрос 1: Что такое квадратный корень?
Ответ:
В математике квадратный корень из любого числа — это значение, которое дает исходное число при умножении на себя. Квадратный корень и квадрат являются обратными операциями. Например, если число «m» — это квадратный корень из числа «n» (m = √n), то «n» — это квадрат числа «m» (n = m × m).
Вопрос 2: Может ли квадратный корень быть отрицательным?
Ответ:
Мы знаем, что квадрат любого числа всегда положителен, поэтому каждое число имеет два квадратных корня, один из которых является положительным значением, а другой — отрицательным. Итак, квадратный корень из числа может быть отрицательным. Например, значение квадратного корня из 9 равно 3 и -3.
Вопрос 3: Что такое символ квадратного корня?
Ответ:
Квадратный корень из x обозначается как √x , где x называется подкоренным числом, а « √ » называется подкоренным символом, который обозначает квадратный корень.
Вопрос 4: Как складывать и вычитать квадратные корни?
Ответ:
Сложение и вычитание квадратных корней можно выполнять так же, как и с обычными числами.