Данный онлайн калькулятор дробей предназначен для сложения, вычитания, деления и умножения между собой обыкновенных дробей. А так же дробей с целой частью и десятичных дробей.
Основные возможности:
- Сложение, вычитание, деление и умножение дробей.
- Расчет дробей с подробнейшим решением.
- Расчет дробей со степенями, скобками и буквами.
- Сокращение дробей.
- Поддержка до трех дробей онлайн.
На данном калькуляторе можно посчитать сложение вычитание деление или умножение дробей.
Калькулятор умеет:
- Вносить целую часть дроби в числитель для смешанных дробей.
- Расчет дробей со скобками- поддержка до двух уровней вложенности скобок.
- Расчет дробей со степенями — степенью может быть только число.
- Расчет дробей с буквами — любые анг. буквы или символы.
- Сокращение дробей — только для дробей без букв.
Основные символы:
- * символ звездочки интерпретируется как умножение.
- / слеш интерпретируется как деление.
- + и — интерпретируются как сложение и вычитание.
- ^ символ интерпретируется как степень.
- ( ) символы интерпретируются как открывающаяся и закрывающаяся скобки.
Подробности:
- Между двумя буквами необязательно ставить знак умножения (если они умножаются). Пример вместо x*x можно написать xx.
- После знака степени ^ должно стоять число степени. Если оно отрицательно необходимо заключить его в скобки. Пример x^2+1 или x^(-2) +1.
- При сложении дробей состоящих только из чисел калькулятор вычисляет НОД и НОК.
- При расчете сразу трех дробей сначала выполняется операция умножение(деления), затем сложения(вычитания). Для изменения этого порядка поставьте галочку в поле «Большие скобки» и выберите нужный порядок расчета. В этом случае первой будет выполняться операция в больших скобках.
Инструкция использования калькулятора дробей
Для решения вашей задачи выполните следующие действия:
- введите ваш пример в калькулятор;
- нажмите кнопку для выполнения вычислений.
Ввод данных в калькулятор дробей
В калькулятор дробей можно вводить: целые числа, десятичные дроби, обыкновенные дроби и смешанные числа.
Целые числа. Для ввода целых чисел используйте цифровые клавиши калькулятора или цифровые клавиши вашего компьютера. 1 2 3 4 5 6 7 8 9 0
Десятичные дроби. Десятичные дроби вводятся также как и целые числа, в качестве десятичного разделителя рекомендуется использовать точку .
Обыкновенные дроби: Для ввода обыкновенной дроби нажмите клавишу на клавиатуре калькулятора — после чего введите значения числителя и знаменателя дроби используя числовые клавиши.
Смешанные числа: Используя числовые клавиши введите целую часть смешанной дроби, нажмите клавишу дроби на клавиатуре калькулятора — после чего введите значения числителя и знаменателя дроби используя числовые клавиши.
Отрицательные числа: Перед числом поставьте знак минус -, не забывайте брать отрицательные числа в скобки ( ).
Возведение в степень: Для возведения числа в степень введите число нажмите клавишу ab, затем введите значение степени. (На компьютере степень можно ввести нажав клавишу «^». Например, для ввода 43 нужно набрать 4^3)
N.B. Калькулятор поддерживает только целые степени!
N.B. Буквенные выражения, операции извлечения корня калькулятор не поддерживает!
Дополнительные возможности калькулятора дробей — старая версия
- С — полностью очистить поле ввода.
- — удалить один символ.
- для перемещения между полями калькулятора.
Калькулятор дробей
Как перевести смешанную дробь в обыкновенную
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: i nd = i · d + nd
Например,
5 34 = 5 · 4 + 34 = 234Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
- Поделить числитель дроби на её знаменатель
- Результат от деления будет являться целой частью
- Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Как перевести десятичную дробь в обыкновенную или смешанную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
- Записать дробь в виде десятичная дробь1
- Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
- Найти наибольший общий делитель и сократить дробь.
Например, переведем 0.36 в обыкновенную дробь:
- Записываем дробь в виде: 0.361
- Умножаем на 10 два раза, получим 36100
- Сокращаем дробь 36100 = 925
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Выполнить сложение дробей путем сложения их числителей.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Калькулятор дробей
Онлайн калькулятор дробей может произвести сложение дробей, вычитание дробей, умножение дробей и деление дробей любого вида как с одинаковыми, так и с разными знаменателями и получить полное пошаговое решение примера
Если у дроби нет целой части, оставьте это поле пустым. Если дробь отрицательная, поставьте минус в целой части. Кнопка (+) дает возможность вставить ответ в дробь и произвести дальнейшие вычисления.
| Вам могут также быть полезны следующие сервисы |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькуляторы (Теория чисел) |
| Калькулятор со скобками |
| Генератор случайных чисел |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер сложения |
| Тренажёр вычитания |
| Тренажёр умножения |
| Тренажёр деления |
| Тренажёр таблицы умножения |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
Примеры действия с дробями
Сложение дробей с одинаковыми знаменателями
Сложим две дроби с одинаковыми знаменателямиСложим числители дробей, а знаменатель оставим прежним
Упростим дробь
Сложение дробей с разными знаменателями
Сложим две дроби с разными знаменателямиПриведем дробиик общему знаменателю, для этого найдем наименьшее общее кратное (НОК) знаменателей первой и второй дроби
НОК( 15 ; 14 ) = 210
Разделим значение НОК 210 на знаменатель первой дроби и на знаменатель второй дроби
210 : 15 = 14
210 : 14 = 15
Теперь запишем в знаменатель каждой дроби НОК( 15 ; 14 ), а числитель каждой дроби умножим на результат деления НОК на соответствующий знаменатель
Упростим дробь
Сложение смешанных дробей с разными знаменателями
Сложим две смешанные дроби с разными знаменателямиПриведем смешанные дроби и к неправильному виду. Для этого у каждой дроби знаменатель оставим прежним, а в числитель запишем сумму, где первое слагаемое произведение знаменателя и целой части, а второе числитель
Приведем дробиик общему знаменателю, для этого найдем наименьшее общее кратное (НОК) знаменателей первой и второй дроби
НОК( 8 ; 12 ) = 24
Разделим значение НОК 24 на знаменатель первой дроби и на знаменатель второй дроби
24 : 8 = 3
24 : 12 = 2
Теперь запишем в знаменатель каждой дроби НОК( 8 ; 12 ), а числитель каждой дроби умножим на результат деления НОК на соответствующий знаменатель
Упростим дробь
Вычитание дробей с одинаковыми знаменателями
Вычтем две дроби с одинаковыми знаменателямиИз числителя первой дроби вычтем числитель второй дроби, а знаменатель оставим прежним
Упростим дробь
Вычитание дробей с разными знаменателями
Вычтем две дроби с разными знаменателямиПриведем дробиик общему знаменателю, для этого найдем наименьшее общее кратное (НОК) знаменателей первой и второй дроби
НОК( 12 ; 9 ) = 36
Разделим значение НОК 36 на знаменатель первой дроби и на знаменатель второй дроби
36 : 12 = 3
36 : 9 = 4
Теперь запишем в знаменатель каждой дроби НОК( 12 ; 9 ), а числитель каждой дроби умножим на результат деления НОК на соответствующий знаменатель
Упростим дробь
Вычитание смешанных дробей с разными знаменателями
Вычтем две смешанные дроби с разными знаменателямиПриведем смешанные дроби и к неправильному виду. Для этого у каждой дроби знаменатель оставим прежним, а в числитель запишем сумму, где первое слагаемое произведение знаменателя и целой части, а второе числитель
Приведем дробиик общему знаменателю, для этого найдем наименьшее общее кратное (НОК) знаменателей первой и второй дроби
НОК( 17 ; 19 ) = 323
Разделим значение НОК 323 на знаменатель первой дроби и на знаменатель второй дроби
323 : 17 = 19
323 : 19 = 17
Теперь запишем в знаменатель каждой дроби НОК( 17 ; 19 ), а числитель каждой дроби умножим на результат деления НОК на соответствующий знаменатель
Упростим дробь
Умножение дробей
Умножим две дробиПеремножим знаменатели и числители дробей
Умножение смешанных дробей
Умножим две смешанные дробиПриведем смешанные дроби и к неправильному виду. Для этого у каждой дроби знаменатель оставим прежним, а в числитель запишем сумму, где первое слагаемое произведение знаменателя и целой части, а второе числитель
Перемножим знаменатели и числители дробей
Упростим дробь
Умножим две дроби
Приведем смешанную дробь к неправильной. Для этого знаменатель дроби оставим прежним, а в числитель запишем сумму, где первое слагаемое произведение знаменателя и целой части, а второе числитель
Перемножим знаменатели и числители дробей
Упростим дробь
Деление дробей
Разделим две дробиПоменяем местами числитель и знаменатель второй дроби
Перемножим знаменатели и числители дробей
Упростим дробь
Деление смешанных дробей
Разделим две смешанные дробиПриведем смешанные дроби и к неправильному виду. Для этого у каждой дроби знаменатель оставим прежним, а в числитель запишем сумму, где первое слагаемое произведение знаменателя и целой части, а второе числитель
Поменяем местами числитель и знаменатель второй дроби
Перемножим знаменатели и числители дробей
Упростим дробь
Разделим две дроби
Приведем смешанную дробь к неправильной. Для этого знаменатель дроби оставим прежним, а в числитель запишем сумму, где первое слагаемое произведение знаменателя и целой части, а второе числитель
Поменяем местами числитель и знаменатель второй дроби
Перемножим знаменатели и числители дробей
Упростим дробь
Калькулятор дробей
Дроби
Что такое дроби и как их решать
Дробь в математике – это число, являющееся частью единицы или несколькими её частями. То есть если мы хотим указать на половину части целого, то мы пишем обыкновенную дробь ½.
Дробью необязательно мы можем указать часть целого. С помощью дроби мы можем обозначить вообще любое число. Например, дробь 4/2 будет равняться двум, то есть целому числу.
Обыкновенная дробь представляет собой два числа, разделенных горизонтальной чертой – знаком деления. Число, которое располагается над чертой, – числитель, а число под чертой – знаменатель. Знаменатель обозначает количество равных частей, на которое делится целое, а числитель дроби – количество взятых частей данного целого для дальнейшего деления на знаменатель.
Дробь может иметь десятичную форму. Например, обыкновенная дробь 1/10 может обозначаться как 0,1 в десятичной форме. Десятичная форма – это рациональное или иррациональное число, обозначающее дробь. Десятичная форма, может иметь бесконечный вид, например, дробь 1/3 имеет в десятично виде бесконечную форму 0,333333333…
Дроби могут быть правильными и неправильными. Правильной называют такую дробь, у которой числитель меньше знаменателя. В случае если числитель дроби больше знаменателя, она называется неправильной. Дробь, записанная в виде целого числа и правильной дроби называется смешанной. А дробь, которая не имеет целую часть, называется простой дробью. Любую смешанную дробь можно преобразовать в неправильную простую дробь.
Так же читайте нашу статью «Калькулятор факториалов онлайн»
Как пользоваться калькулятором дробей?
Воспользоваться калькулятором дробей вы всегда сможете на сайте pocketteacher.ru. Бесплатный онлайн решатель позволит решить дробное выражение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Сложение дробей | Онлайн калькулятор
Сложение дробей с одинаковыми знаменателями:
Определение: Суммой дробей с одинаковыми знаменателями называют дробь,числитель которой равен сумме числителей исходных дробей,и со знаменателем равным знаменателю обеих дробей.Формула 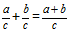
Сложим две дроби с одинаковым с одинаковыми знаменателями 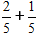
По формуле складываем числители, а знаменатель оставляем исходный 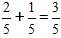
Важно: Если есть возможность сократить дробь, то в конечный ответ мы записываем сокращенную дробь.
Пример: 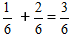 При сокращении дроби у нас получится число 1/2
При сокращении дроби у нас получится число 1/2
Сложение дробей с разными знаменателями:
Определение: Для того, чтобы найти сумму дробей с разными знаменателями сначала нужно дроби привести к общему знаменателю, а затем сложить их как дроби с одинаковыми знаменателями.Задача:
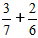
Ход решения:
1) Приводим дроби к общему знаменателю.
Для этого ищем НОК — наименьшее общее кратное, для знаменателей 7 и 6 это число 42.
Делим число 42 на знаменатели дробей 3/7 и 2/6
Так мы нашли дополнительные множители.
Дальше домножаем дроби на дополнительные множители и получаем выражение: 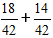
2) Складываем дроби.
В нашем случае дробь можно сократить на 2 , и в конечный ответ записываем число 16/21
Сложение дроби и целого числа:
Определение: Для того, чтобы сложить дробь с целым числом, нужно сначала представить целое число как дробь со знаменателем равным 1.Алгоритм расчета:
1) Приводим дроби к общему знаменателю.
2) Складываем дроби 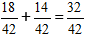
3) Если есть возможность, то сокращаем полученную дробь.
4) Если же получилась неправильная дробь, то вычисляем из нее целую часть.
Пример: 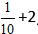
Решение: 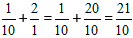
Вычисляем целую часть, и получаем ответ 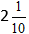
Сложение смешанных дробей:
Определение: Для того, чтобы сложить смешанные дроби нужно отдельно сложить целые части, и отдельно сложить дробные части.Формула
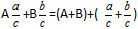
Пример:
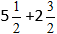
Подставляем цифры в формулу:
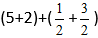
Получаем:
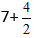
Из дроби вычисляем целую часть т.к она неправильная,и получаем выражение 7+2=9.
Сложение дробей с помощью онлайн калькулятора:
Смотрите также
Калькулятор фракцийКалькулятор Использование
Используйте этот калькулятор для сложения, вычитания, умножения и деления дробей. Ответы — это дроби в самых низких терминах или смешанные числа в сокращенной форме.
Введите правильные или неправильные дроби, выберите математический знак и нажмите «Рассчитать». Это калькулятор фракций с шагами, показанными в решении.
Если у вас есть отрицательные дроби, вставьте знак минуса перед числителем.Поэтому, если одна из ваших дробей равна -6/7, вставьте -6 в числитель и 7 в знаменатель.
Иногда математические задачи включают слово «из», как в Что такое 1/3 от 3/8? от означает, что вы должны умножить, поэтому вам нужно решить 1/3 × 3/8.
Для математики со смешанными числами (целыми числами и дробями) используйте Калькулятор смешанных чисел.
Математические дроби с отличными от знаменателями
В двух случаях вам нужно знать, имеют ли ваши дроби разные знаменатели:
- , если вы добавляете дроби
- , если вы вычитаете дроби
Как сложить или вычесть дроби
- Найдите наименьший общий знаменатель
- Вы можете использовать ЖК-калькулятор, чтобы найти наименьший общий знаменатель для набора фракций
- Для вашей первой дроби найдите, на какое число нужно умножить знаменатель, чтобы получить наименьший общий знаменатель
- Умножьте числитель и знаменатель вашей первой дроби на это число
- Повторите шаги 3 и 4 для каждой фракции
- Для сложения уравнений добавьте числители дроби
- Для уравнений вычитания вычтите числители дроби
- Преобразование неправильных дробей в смешанные числа
- Снизить дробь до самых низких сроков
Как умножить дроби
- Умножьте все числители вместе на
- Умножьте все знаменатели вместе на
- Снизить результат до самых низких сроков
Как разделить дроби
- Запишите уравнение, как в «Сохранить, изменить, перевернуть»
- Keep первая фракция
- Измените знак деления на умножение
- Flip вторая дробь путем переключения верхних и нижних чисел
- Множить все числители вместе
- Умножьте все знаменатели вместе на
- Снизить результат до самых низких сроков
Fraction Formulas
Есть способ складывать или вычитать дроби, не находя наименьший общий знаменатель (ЖК).Этот метод предполагает кросс-умножение дробей. Смотрите формулы ниже.
Вы можете обнаружить, что эти формулы проще использовать, чем вычислять, чтобы найти наименьший общий знаменатель.
Формулы для умножения и деления дробей следуют тому же процессу, что и описанный выше.
Формула для добавления фракций:
\ (\ dfrac {a} {b} + \ dfrac {c} {d} = \ dfrac {ad + bc} {bd} \)
Примеры шагов:
\ (\ dfrac {2} {6} + \ dfrac {1} {4} = \ dfrac {(2 \ times4) + (6 \ times1)} {6 \ times4} \)
\ (= \ dfrac {14} {24} = \ dfrac {7} {12} \)
Формула для вычитания фракций:
\ (\ dfrac {a} {b} — \ dfrac {c} {d} = \ dfrac {ad — bc} {bd} \)
Примеры шагов:
\ (\ dfrac {2} {6} — \ dfrac {1} {4} = \ dfrac {(2 \ times4) — (6 \ times1)} {6 \ times4} \)
\ (= \ dfrac {2} {24} = \ dfrac {1} {12} \)
Формула для умножения дроби:
\ (\ dfrac {a} {b} \ times \ dfrac {c} {d} = \ dfrac {ac} {bd} \)
Примеры шагов:
\ (\ dfrac {2} {6} \ times \ dfrac {1} {4} = \ dfrac {2 \ times1} {6 \ times4} \)
\ (= \ dfrac {2} {24} = \ dfrac {1} {12} \)
Формула для разделения фракций:
\ (\ dfrac {a} {b} \ div \ dfrac {c} {d} = \ dfrac {ad} {bc} \)
Примеры шагов:
\ (\ dfrac {2} {6} \ div \ dfrac {1} {4} = \ dfrac {2 \ times4} {6 \ times1} \)
\ (= \ dfrac {8} {6} = \ dfrac {4} {3} = 1 \ dfrac {1} {3} \)
Связанные калькуляторы
Для выполнения математических операций над смешанными дробями используйте наш Калькулятор смешанных чисел.Обратите внимание, что знаменатель дроби не может быть 0, так как это сделает дробь неопределенной. Фракции могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.
Addition:
В отличие от сложения и вычитания целых чисел, таких как 2 и 8, дроби требуют общего знаменателя для выполнения этих операций. Уравнения, представленные ниже, учитывают это путем умножения числителей и знаменателей всех дробей, участвующих в сложении, на знаменатели каждой дроби (исключая умножение себя на собственный знаменатель).Альтернативой использованию этого уравнения в случаях, когда дроби несложны, было бы найти наименьшее общее кратное, а затем сложить или вычесть числители как одно целое число. В зависимости от сложности дробей, поиск наименьшего общего множителя для знаменателя может быть более эффективным, чем использование уравнений. Обратитесь к уравнениям ниже для уточнения.
Subtraction:
Вычитание фракции по существу такое же, как и сложение фракции. Для выполнения операции требуется общий знаменатель.Обратитесь к разделу дополнения, а также приведенным ниже уравнениям для уточнения.
— = ( × ) — ( × ) = Multiplication:
Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат формирует новый числитель и знаменатель.Если возможно, решение должно быть упрощено. Обратитесь к уравнениям ниже для уточнения.
Division:
Процесс деления дроби аналогичен процессу умножения дроби. Чтобы разделить дроби, дробь в числителе умножается на обратную дробь в знаменателе. Ответное число a просто
. Когда а является дробью, это по существу включает в себя обмен положения числителя и знаменателя.Таким образом, обратная дробь будет. Обратитесь к уравнениям ниже для уточнения.Simplification:
Часто проще работать с упрощенными дробями. Таким образом, растворы фракций обычно выражаются в их упрощенных формах.
например, более громоздко, чем. Предоставленный калькулятор возвращает входные данные дроби как в неправильной форме дроби, так и в смешанной числовой форме. В обоих случаях дроби представлены в их младших формах путем деления числителя и знаменателя на их наибольший общий множитель.Преобразование между дробями и десятичными:
Преобразование из десятичных дробей в дробные несложные. Однако требуется понимание того, что каждое десятичное место справа от десятичной точки представляет степень 10; первое десятичное место — 101, второе — 102, третье — 103 и т. д. Просто определите, к какой степени 10 относится десятичное число, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Зная, что первое десятичное место представляет 101, можно конвертировать в 0.5. Если бы вместо этого была дробь, то десятичная дробь тогда была бы 0,05, и так далее. Помимо этого, преобразование дробей в десятичные дроби требует операции длинного деления.
Общая инженерная дробь в десятичные преобразования
В машиностроении дроби широко используются для описания размеров компонентов, таких как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже.
64th 32nd 16th 8th 4th 2nd Decimal Decimal
(дюйм в мм)1/64 0.171875 4,365625 12 / 64 6/32 3/16 0.1875 4.7625 13 / 64 0.203125 5.159375 14 / 64 7/32 0.21875 5.55625 15 / 64 0.234375 5.953125 16 / 64 8/32 4/16 2/8 1/4 0.25 6,35 17 / 64 0.265625 6.746875 18 / 64 9/32 0.28125 7.14375 19 / 64 0.296875 7.540625 20 / 64 10/32 5/16 0.3125 7.9375 21 / 64 0.328125 8,334375 22 / 64 11/32 0.34375 8.73125 23 / 64 0.359375 9.128125 24 / 64 12/32 6/16 3/8 0.375 9.525 25 / 64 0.3 9.921875 26 / 64 13/32 0. Добавить, вычесть, разделить и умножить дроби
Инструкции по использованию
- Введите свои дроби в калькулятор выше.
- Выберите математическую операцию, которую вы хотите выполнить (сложить, вычесть, умножить, разделить), используя выпадающий список серого цвета между двумя фракциями.
- Результаты будут обновляться автоматически при изменении любого значения в калькуляторе. Чекбокс
- A под калькулятором позволяет вам выбирать между уменьшением дроби до наименьшего эквивалента общего знаменателя (если отмечено) или не уменьшением (если не отмечено).

Как вычислить дроби вручную
Как добавить фракции
- Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
- Умножьте каждый числитель на те же числа, на которые умножены знаменатели.
- Добавьте числители вместе.
- Снизить результат до максимально упрощенного числа.
Как вычесть дроби
- Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
- Умножьте каждый числитель на те же числа, на которые умножены знаменатели.
- Добавить второй числитель из первого.
- Снизить результат до максимально упрощенного числа.
Как умножить дроби
- Умножьте числа через вершину вместе.
- Умножьте числа внизу вместе.
- Снизить результат до максимально упрощенного числа.
Как разделить дроби
- Переверните вторую дробь вверх дном, чтобы создать обратное число.
- Умножьте дроби вместе (как в разделе умножения выше) .
- Снизить результат до максимально упрощенного числа.
Фракции: история, актуальность и популярное использование
— Руководство Автор Corin B. Arenas, опубликовано 22 октября 2019 г.
Мы практически каждый день имеем дело с дробями. Думаю об этом. Независимо от того, получаете ли вы четверть за смену, покупаете одежду со скидкой 75% или готовите с полстакана масла, вы используете фракции.
В этом разделе мы поговорим о происхождении дроби, ее важности для доставки информации и золотом сечении.
Что такое дроби?
Fractions представляют части целого числа или любое количество равных частей. Это функционирует описать, как части связаны с целым числом.
Чтобы проиллюстрировать, представьте себе целое число как торт. Если вы нарежете торт на 4 равные части, один кусок будет частью этого торта. В данном случае это 1/4 от всего торта.

- 1 представляет один фрагмент или часть целого числа, которое называется numerator.
- 4 представляет, сколько всего частей в целом числе, которое называется denominator.

A Краткая история фракций
Слово происхождения: Термин фракция происходит от латинского слово fractio что означает «ломать». В раннем английском языке это означает «отломанный кусок или фрагмент «. Английское слово» перелом «также имеет то же слово origin.
Концепция дробей существует уже более 4000 лет. Но разные цивилизации имеют свой собственный способ стандартизации фракций для универсального использования.
Egyptians

Согласно Математика сквозь века : Нежная история для учителей и других, египтяне были одними из первых, кто изобрел форму дроби еще в 1800 году до нашей эры.
- Умножьте все знаменатели вместе на