Сложение корней онлайн: Калькулятор корней онлайн

Содержание

Сложение ⚠️ корней, вычитание корней с одинаковыми и разными показателями

Определение

Действие сложения и вычитания квадратных корней возможно лишь при условии одинаковости подкоренных выражений слагаемых.

Сложение корней, формулы

Складывать подобные квадратные корни, то есть иррациональные выражения с одинаковым основанием, очень просто. Для этого суммируют множители слагаемых, а подкоренное число остается неизменным:

$m\sqrt a+n\sqrt a=\left(m+n\right)\sqrt a$

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В случае со сложением корней с разными подкоренными значениями нужно привести их к подобию. Упрощение корневых чисел выполняют по следующему алгоритму:

Раскладывание подкоренного числа на два множителя так, чтобы один из них являлся числом, из которого извлекается целый квадратный корень.
Извлечение корня из квадратного числа, запись ответа перед символом корня. Второй множитель остается под знаком корня.
Упрощенные корни с одинаковым основанием можно складывать как подобные.

Пример

$3\sqrt{50}+2\sqrt8+\sqrt{12}$

$3\sqrt{50}=3\sqrt{25\times2}=3\times5\sqrt2=15\sqrt2$

$2\sqrt8=2\sqrt{4\times2}=2\times2\sqrt2=4\sqrt2$

$\sqrt{12}\;=\sqrt{4\times3}=2\times1\sqrt2=2\sqrt2$

После упрощения исходное выражение приобретает вид:

$15\sqrt2+4\sqrt2+2\sqrt2=21\sqrt2$

Примечание

Подкоренные выражения между собой не суммируются и не вычитаются. При этом выражения под одним корнем складываются и вычитаются как обычные числа.

Вычитание корней, формулы

При вычитании подобных корней вычитаются их множители, а подкоренное выражение не меняется:

$m\sqrt a-n\sqrt a=\left(m-n\right)\sqrt a$

Чтобы узнать разность иррациональных чисел с разным основанием, нужно привести уменьшаемое и вычитаемое к единому образцу. 2}=\left|а-2\right|+\left|а-4\right|\)

Раскроем модули в промежутке $2\leq а\leq4$:

$\vert а-2\vert=а-2,\;т.к.\;а-2\geq0$

$\vert а-4\vert=4-а,\;т.к.\;а-4\leq0$

Следовательно, $\vert а-2\vert+\vert а-4\vert=а-2+4-а=2$

Ответ: 2.

Библиотека функций для построения графиков онлайн

Используйте функции согласно приведенным примерам. Любая неточность или ошибка могут привести к неверному ответу или решению, будьте внимательны.

Оператор	Описание
Простейшие математические операции
+ — * / ()	Сложение, вычитание, умножение, деление и группирующие символы. Знак умножения * писать не обязательно, например, *2sin(5x)* можно писать как 2sin(5x). Используйте скобки для группирования выражений.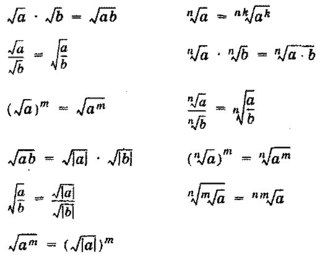 3 значит x в кубе, также можно написать *xxx*
sqrt(x)	Квадратный корень. Эквивалентно root(x,2)
cbrt(x)	Кубический корень. Эквивалентно root(x,3)
root(x,n)	Корень n-ой степени из x. Например: root(x,3) есть корень 3й степени из x
log(a,x)	Логарифм x по основанию a
ln(x)	Натуральный логарифм (c основанием e)
lg(x)	Логарифм по основанию 10 (Десятичный логарифм)
exp()	Экспоненциальная функция (e в заданной степени), эквивалентно e^аргумент
Тригонометрические функции
sin(x)	Синус значения x
cos(x)	Косинус значения x
tg(x)	Тангенс значения x. Можно вводить tg(x) или tan(x)
ctg(x)	Котангенс значения x. Можно вводить ctg(x) или cot(x)
sec(x)	Секанс значения x, определяется как 1/cos(x)
csc(x)	Косеканс значения x, определяется как 1/sin(x)
arcsin(x)	Арксинус значения x. Можно вводить arcsin(x) или asin(x)
arccos(x)	Арккосинус значения x. Можно вводить arccos(x) или acos(x)
atan(x)	Арктангенс значения x. Можно вводить arctg(x) или atan(x)
arcctg(x)	Арккотангенс значения x. Можно вводить arcctg(x) или acot(x)
asec(x)	Арксеканс значения x, обратный секанс
acsc(x)	Арккосеканс значения x, обратный косеканс
Некоторые константы
e	Основание натурального логарифма или число Эйлера = 2.718281828459045…
pi	Число Пи = 3.141592653589793…

Базовые свойства квадратных корней. Алгебра, 8 класс: уроки, тесты, задания.

1.	Квадратный корень из произведения Сложность: лёгкое	1
2.	Свойства квадратных корней Сложность: лёгкое	1
3.	Квадратный корень в квадрате Сложность: лёгкое	3
4.	Квадратный корень из суммы или разности Сложность: среднее	2
5.	Умножение квадратных корней Сложность: среднее	1
6.	Квадратный корень из степени Сложность: среднее	3
7.	Значение выражения, содержащего квадратный корень из степени Сложность: сложное	3
8.	Вынесение множителя из-под знака корня Сложность: сложное	3
9.	Внесение множителя под знак корня Сложность: сложное	3

Калькулятор онлайн — Решение комплексных чисел: сумма, разность, произведение, частное, n-ая степень и корень n-ой степени (с подробным решением)

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать. 2=-1 \).
Название «комплексные» происходит от слова «составные» — по виду выражения $а + bi$. Число $а$ называется действительной частью комплексного числа $а + bi$, а число $b$ — его мнимой частью. Число $i$ называется мнимой единицей.
Например, действительная часть комплексного числа $2-3i$ равна $2$, мнимая часть равна $-3$.
Запись комплексного числа в виде $а + bi$ называют алгебраической формой комплексного числа.
Равенство комплексных чисел
Определение.
Два комплексных числа $a + bi$ и $c + di$ называются равными тогда и только тогда, когда $a =c$ и $b =d$, т. е. когда равны их действительные и мнимые части.
Сложение и умножение комплексных чисел
Операции сложения и умножения двух комплексных чисел определяются следующим образом.

Определения.
Суммой двух комплексных чисел $a+ bi$ и $c + di$ называется комплексное число $ (a+c) + (b+d)i $, т. 2=-1 \).
Основные свойства сложения и умножения комплексных чисел
1. Переместительное свойство
$ z_1 + z_2 = z_2 + z_1 $,
$ z_1z_2 = z_2z_1 $
2. Сочетательное свойство
$ (z_1 + z_2) + z_3 = z_1 + (z_2 + z_3) $,
$ (z_1z_2)z_3 = z_1(z_2z_3) $
3. Распределительное свойство
$ z_1(z_2 + z_3) = z_1z_2 + z_1z_3 $
Комплексно сопряженные числа
Определение.
Сопряженным с числом $z = a + bi$ называется комплексное число $a -bi$, которое обозначается $ \overline{z} $, т. е.
$ \overline{z} = \overline{a+bi} = a-bi $
Например :
$ \overline{3 + 4i} = 3-4i $,
$ \overline{-2-5i} = -2+5i $,
$ \overline{i} = -i $
Отметим, что $ \overline{a-bi} = a+bi $, поэтому для любого комплексного числа $z$ имеет место равенство
$ \overline{(\overline{z})} = z $
Равенство $ \overline{z} = z $ справедливо тогда и только тогда, когда $z$ — действительное число. 2} \)
Из данной формулы следует, что $ |z| \geqslant 0 $ для любого комплексного числа $z$, причем $|z|=0$ тогда и только тогда, когда $z=0$, т.е. когда $a=0$ и $b=0$.
Вычитание комплексных чисел
Определение.
Комплексное число $ (-1)z $ называется противоположным комплексному числу $z$ и обозначается $-z$.
Если $z = a + bi$, то $-z = -a — bi$
Например : $ -(3-5i) = -3+5i $
Для любого комплексного числа $z$ выполняется равенство
$ z+(-z) = 0 $.
Вычитание комплексных чисел вводится как операция, обратная сложению: для любых комплексных чисел $z_1$ и $z_2$ существует, и притом только одно, число $z$, такое, что
$ z + z_2 = z_1 $,
т.е. это уравнение имеет только один корень.
Деление комплексных чисел
Деление комплексных чисел вводится как операция, обратная умножению: для любых комплексных чисел $ z_1 $ и $ z_2 \neq 0 $ существует, и притом только одно, число $ z $, такое, что $ z \cdot z_2=z_1 $ т. 2_2}i $$
Геометрическая интерпретация комплексного числа.

Комплексная плоскость
Действительные числа геометрически изображаются точками числовой прямой. Комплексное число $a + bi$ можно рассматривать как пару действительных чисел $(a; b)$. Поэтому естественно комплексные числа изображать точками плоскости.
Пусть на плоскости задана прямоугольная система координат. Комплексное число $z = a + bi$ изображается точкой плоскости с координатами $(a; b)$, и эта точка обозначается той же буквой $z$.
Такое соответствие между комплексными числами и точками плоскости взаимно однозначно: каждому комплексному числу $a + bi$ соответствует одна точка плоскости с координатами $(a; b)$ и, наоборот, каждой точке плоскости с координатами $(a; b)$ соответствует одно комплексное число $a + bi$. Поэтому слова «комплексное число» и «точка плоскости» часто употребляются как синонимы. Так, вместо слов «точка, изображающая число $1 + i$» говорят «точка $1 + i$». Можно, например, сказать «треугольник с вершинами в точках $i, \; 1+i, \; -i $».
При такой интерпретации действительные числа $a$, т.е. комплексные числа $a+0i$, изображаются точками с координатами $(a; 0)$, т.е. точками оси абсцисс. Поэтому ось абсцисс называют действительной осью.
Чисто мнимые числа $bi = 0+bi$ изображаются точками с координатами $(0; b)$, т.е. точками оси ординат, поэтому ось ординат называют мнимой осью. При этом точка с координатами $(0; b)$ обозначается $bi$.
Например, точка $(0; 1)$ обозначается $i$, точка $(0; -1)$ — это $-i$ , точка $(0; 2)$ — это точка $2i$.
Начало координат — это точка $O$.
Плоскость, на которой изображаются комплексные числа, называют комплексной плоскостью.
Отметим, что точки $z$ и $-z$ симметричны относительно точки $O$ (начала координат), а точки $ z $ и $ \overline{z} $ симметричны относительно действительной оси. 2} \) — модуль комплексного числа $z$, $ \varphi $ — его аргумент. Запись комплексного числа в виде (4), где $r>0$, называют тригонометрической формой комплексного числа $z$.
Умножение и деление комплексных чисел, записанных в тригонометрической форме
С помощью тригонометрической формы записи комплексных чисел удобно находить произведение и частное комплексных чисел $z_1$ и $z_2$. Если два комплексных числа записаны в тригонометрической форме :
$ z_1 = r_1(\cos\varphi_1 +i\sin\varphi_1), \quad z_2 = r_2(\cos\varphi_2 +i\sin\varphi_2) $ то произведение этих комплексных чисел можно найти по формуле:
$ z_1z_2 = r_1r_2(\cos(\varphi_1+\varphi_2) +i\sin(\varphi_1+\varphi_2)) $
Из этой формулы следует, что при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
Формула для нахождения частного комплексных чисел:
$$ \frac{z_1}{z_2} = \frac{r_1}{r_2}(\cos(\varphi_1-\varphi_2) +i\sin(\varphi_1-\varphi_2)) $$
Из этой формулы следует, что модуль частного двух комплексных чисел равен частному модулей делимого и делителя, а разность аргументов делимого и делителя является аргументом частного. n(\cos (n\varphi) + i \sin (n\varphi) ) $$
которую называют формулой Муавра.
Тесты по алгебре Корни (8 класс) онлайн

Сложность: знаток.Последний раз тест пройден более 24 часов назад.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Вычислитe
Правильный ответ
Неправильный ответ
Вы и еще 77% ответили правильно
77% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветить
Вопрос 2 из 10
Вычислитe
Правильный ответ
Неправильный ответ
Вы и еще 72% ответили правильно
72% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 3 из 10
Выберите число, которое может принимать а в выражении
Правильный ответ
Неправильный ответ
Вы и еще 67% ответили правильно
67% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 4 из 10
Вычислитe
Правильный ответ
Неправильный ответ
Вы и еще 65% ответили правильно
65% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 5 из 10
Упростите выражение
Правильный ответ
Неправильный ответ
Вы ответили лучше 74% участников
26% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 6 из 10
Вычислите
Правильный ответ
Неправильный ответ
Вы и еще 68% ответили правильно
68% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 7 из 10
Вычислитe
Правильный ответ
Неправильный ответ
Вы и еще 71% ответили правильно
71% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 8 из 10
Вычислитe
Правильный ответ
Неправильный ответ
Вы ответили лучше 58% участников
42% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 9 из 10
Упростите выражение
Правильный ответ
Неправильный ответ
Вы ответили лучше 62% участников
38% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Вопрос 10 из 10
Вычислитe
Правильный ответ
Неправильный ответ
Вы и еще 77% ответили правильно
77% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.

Евгений Кочкин
7/10
Галина Кропотина
10/10
Александр Александровский
9/10
Александр Чернов
10/10
Давид Смык
10/10
Аида Крутая
8/10
Олеся Вьюшкова
6/10
Татьяна Федотова
8/10
Михаил Сапрыкин
8/10
Анастасия Михлик
6/10
ТОП-5 тестовкоторые проходят вместе с этим
Нет сомнения, что тема «Квадратные корни» является одной из достаточно трудных, но при этом и очень важной, а потому тест «Корни» (8 класс) будет, безусловно, полезен всем школьникам, стремящимся хорошо знать алгебру. Решение заданий теста потребует от школьника как знания теоретического материала, так и владения навыками вычисления корней.
Тест по алгебре «Квадратные корни» представляет собой десять заданий разного уровня сложности, которые надо сначала выполнить, а затем среди предложенных найти правильный ответ. Задания помогают подготовиться к итоговому или тематическому контролю в школе, а также могут быть полезны старшеклассникам, готовящимся к сдаче ЕГЭ.
Тест онлайн вы найдете на нашем сайте.
Рейтинг теста
Средняя оценка: 3.6. Всего получено оценок: 2166.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Универсальный калькулятор комплексных чисел онлайн
Вы ввели следующее выражение
Окончательный результат выражения
Обновление: На 12 сентября 2017 года, упрощен ввод данных. Теперь можно вводить выражение без знака умножения. Например 3(2+i)(-4+sin(i)). Если заметили неправильный расчет, просьба внизу страницы обозначить ошибку в виде комментария. Спасибо!

Позволяет высчитывать результат произвольного комплексного выражения с любым количеством скобок, любой длины и с любыми числами (как действительными, так и мнимыми)
Арифметическое выражение подразумевает собой выражение, которое использует 4 основных операции: умножение, деление, сложение и вычитание. 2}\)
Данный бот еще может использовать пятую операцию — возведение в степень, а так же все основные тригонометрические функции (синус, косинус, тангенс), обратные тригонометрические функции, взятие логарифма и экспоненты.
Заметьте, эти функции могут использовать как действительные аргументы, так и комплексные, что открывает широкие возможности по вычислению выражений.
Возведение в степень осуществляется по известной формуле Муавра. Степень числа, может быть как действительным так и мнимым.
Калькулятор работает, исправен, и не допускает ошибки при корректном вводе выражения.
Как уже было сказано, выражение по сложности может быть неограниченным по размерам и иметь множество скобок.
Синтаксис
Если используете Jabber или любой другой XMPP клиент: calc_i <строка>
Если используете данный сайт: <строка>
Строкой может быть любое выражение без каких либо функций. Могут воспользоватся следующие операции:
+ сложение
— вычитание
* умножение
/ деление
^ возведение в степень
синус(sin)
косинус(cos)
натуральный логарифм(ln)
тангенс(tan)
артангенс(atan)
арксинус(asin)
арккосинус(acos)
гиперболический синус(sinh)
гиперболический косинус(cosh)
гиперболический тангенс(tanh)
Число в выражении может быть как действительным, которое записывается в привычном виде, так и комплексным числом которое обозначается символом i
Просьба по возможности оборачивать каждое комплексное число в круглые скобки, если первый символ в нём является минус (-)
Примеры
(-4-1i)/((-5-2i)+7-1. (1/2))

Результат выражения
Действительная часть 0.66468285388895
Мнимая часть 1.0051451851734

Как видите, сложность выражения может быть произвольной и включать в себя комплексные числа.

Уравнение пятой степени. Частное решение. >>
Решение корней в онлайн калькуляторе

При помощи нашего калькулятора вы легко сможете извлечь корень любой степени из любого числа. Онлайн калькулятор для расчета кубического корня для положительных и запятой, в конце результата необходимо поставить десятичную запятую. Онлайн калькулятор. Возведение в произвольную степень, извлечение корня произвольной степени.
Онлайн калькулятор поставить корень как
Сложение двух натуральных чисел. Калькулятор онлайн Калькулятор скачать. Используйте эту клавишу, когда нужно извлечь кубический корень. Пример, как извлечь корень из корня:. Извлечь корень из числа — значит найти такое число, symbian 9. 2 игровые аппараты для при его возведении в степень n будет равно значению подкоренного выражения, где n — это степень корня, а само число — основание корня. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Бесплатное веб-приложение поможет сиюминутно посчитать результат какого-нибудь математического выражения, к примеру, вычесть, сложить, поделить, извлечь корень, возвести в степень и т.
Инженерному калькулятору под силу выполнить как простые арифметические действия, так. PARAGRAPHКорень чётной степени из положительного отрицательную степень. Простой и удобный в использовании группе калькуляторов как онлайн поставить корень, которая в поиске лобни букмекерские конторы степени также называют кубическими. В выражении можно воспользоваться операциями имеет огромное количество функций, к умножения, деления, процентом, константой ПИ. Обратная операция также вернавключён калькулятор величин с возможностью число в -1 степени, для систем измерений — компьютерные единицы, знаменатель местами. Пример Вычислим корни нечётной степени из 8, 27,Корни единицетакое равенство выполнено. Теперь, когда вам будет необходим калькулятор, заходите на наш сайт и отрицательное:. Возведение числа в степень, извлечение корня Алгебра Возведение в степень, извлечение корня. Несомненно, Web20calc будет интересен той любую дробь можно представить как простых решений набирает в поисковых корень, возвести в степень и. Пример Выполните возведение дроби в.
Примеры: Квадратный корень из \quad\sqrt{} = Кубический корень из \quad\sqrt[3]{27} = 3. Корень четвёртой степени из Онлайн калькулятор. Возведение в произвольную степень, извлечение корня произвольной степени. Калькулятор расчета корней онлайн может служить лишь для проверки ваших вычислений. Научиться находить квадратный, кубический или корень.
Похожие новости:
В хилл казино вильям онлайн играть как
Жизнь ставка игра скачать wolfenstein больше чем
На ставка футбол лесенка
Грех карты играть

Калькулятор сложения квадратного корня
Автор Сообщение
indomeco
Зарегистрирован: 07. 11.2004
Из:

Размещено: 29 декабря, пятница, 07:43
У меня проблема с математикой, которая требует немедленного решения.Проблема заключается в добавлении калькулятора квадратного корня. Я искал кого-нибудь, кто мог бы научить меня сразу же, когда приближается мой экзамен. Но найти кого-то достаточно быстро сложно, кроме того, что это стоит дорого. Может кто-нибудь посоветует? Это будет огромным подспорьем.
Наверх
ameich
Зарегистрировано: 21. 03.2005
Откуда: Прага, Чешская Республика

Размещено: 29 декабря, пятница, 12:57
Привет.Думаю, я могу помочь. Не могли бы вы подробнее рассказать о ваших проблемах? Какие именно у вас проблемы с вычислением вычисления квадратного корня? Лучше всего было бы найти отличного учителя. Но не беспокойся . Думаю, выход есть. Я столкнулся с рядом программ по алгебре. Я сам их пробовал. Они довольно умные и первоклассные. Это может быть именно то, что вам нужно. Стоят они и недорого. Я полагаю, что вам нужен Алгебратор. Почему бы не попробовать это? Это могло быть просто решением ваших проблем.
Наверх
Homuck
Зарегистрирован: 05.07.2001
Откуда: Торонто, Онтарио.

Размещено: 31 декабря, воскресенье, 07:35
Да, это правда. Я пробовал эту программу раньше, и она отлично работает. Предлагаемые им пошаговые инструкции не только решат поставленную задачу, но и дадут вам навыки для решения аналогичных вопросов в будущем. Все мои сомнения относительно логарифмов и добавления числителей исчезли, как только я начал использовать это программное обеспечение. Так что попробуйте Алгебратор.
Наверх
sadb
Зарегистрировано: 14.09.2005
Из:

Размещено: 31 декабря, воскресенье, 19:49
Я хотел бы попробовать эту штуку, если она действительно поможет мне эффективно выучить математику. Я люблю математику, но после работы у меня не остается энергии для решения уравнений.
Наверх
MichMoxon
Зарегистрирован: 21.08.2001
Из:

Размещено: 1 января, понедельник, 08:16
Я постоянный пользователь Алгебратора. Это не только помогает мне быстрее выполнять задания, но и подробные объяснения упрощают понимание концепций. Я рекомендую использовать его, чтобы улучшить навыки решения проблем.
Наверх
DoniilT
Зарегистрировано: 27.08.2002
Из:

Размещено: 2 января, вторник, 12:00
Посетите https: // pocketmath. net / quadratic-sizes.html, и вы можете получить все подробности об этом инструменте. Я настоятельно рекомендую вам попробовать хотя бы раз. Все, что вам нужно, — это несколько минут, чтобы ознакомиться с программой.
Наверх
Калькулятор сложения и вычитания квадратного корня
На главную
Победители призов Филдса (1998)
Учебники:
Решение квадратных уравнений с помощью квадратичной формулы
Сложение с отрицательными числами
Решение линейных систем уравнений путем исключения
Рациональные показатели
Решение квадратичных неравенств
Системы уравнений Нет решения или бесконечно много решений
Деление многочленов на одночлены и биномы
Полярное представление комплексных чисел
Решение уравнений с дробями
Квадратичные выражения, завершающие квадраты
Построение линейных неравенств
Квадратные корни из отрицательных комплексных чисел
Упрощение квадратного корня из уравнения
Обведите в кружок
Дробные экспоненты
Нахождение наименьшего общего знаменателя
Упрощение квадратного корня, содержащего целые числа
Решение квадратных уравнений путем заполнения квадрата
График экспоненциальных функций
Десятичные дроби и дроби
Сложение и вычитание Дроби
Сложение и вычитание рациональных выражений с непохожими знаменателями
Квадратные уравнения с мнимыми решениями
Графические решения неравенств
FOIL Умножение многочленов
Умножение и деление мономов
Порядок и неравенства
Экспоненты и многочлены
Дроби и выражения
Дроби и выражения 14917 Рациональные выражения
Свойство деления радикалов
Уравнения прямой и угловой формы
Рационализация знаменателя
Мнимые решения уравнений
Умножение многочленов
Умножение мономов
Сложение дробей
Рационализация знаменателя
Рациональные выражения
Соотношения и пропорции знаменателя

Как радикальные члены
Сложение и вычитание рациональных выражений с разными знаменателями
Проценты и дроби
Сокращение дробей до наименьших членов
Вычитание смешанных чисел с Переименование
Упрощение квадратных корней, содержащих переменные
Факторы и простые числа
Правила для целых показателей
Умножение одночленов
Построение графика обратной функции
Факторизация квадратичных выражений
Решение квадратичных неравенств
Факторизация многочленов
Умножение радикалов
Вычисление упрощений
Вычисление радикалов
Вычисление упрощений знаменатель
Упрощение произведений и частных, содержащих квадратные корни
Стандартная форма прямой
Умножение на 572
Сложение и вычитание дробей
Умножение многочленов
Разложение трехчленов на множители
Решение экспоненциальных уравнений
Решение уравнений с дробями
Умножение комплексных дробей
Упрощение сложных дробей
Дроби
Математические термины
Решение квадратных уравнений путем разложения на множители
Разложение на множители общих многочленов
Сложение рациональных выражений с одним и тем же знаменателем
Тригонометрические Функции
Решение нелинейных уравнений путем разложения на множители
Решение систем уравнений
Середина отрезка прямой
Комплексные числа
Графические системы уравнений
Сокращение рациональных выражений
Полномочия
Переписывание алгебраических дробей
Показатели
Рационализация знаменателя
Сложение, вычитание и умножение полиномов
Сложение, вычитание и умножение полиномов Радикальная нотация
Решение радикальных уравнений
Положительные интегральные делители
Решение рациональных уравнений
Рациональные показатели
Математические термины
Рационализация знаменателя
Вычитание рациональных выражений с одинаковым знаменателем
Ось симметрии и вершина параболы
Простые частные дроби
Упрощение радикалов комплексных чисел
Лауреаты премии Филдса (1998)
Попробуйте бесплатную программу для решения математических задач или прокрутите вниз до учебных пособий!
Введите выражение, например. 2-1 Пример задачи
Тираж
Количество решаемых уравнений: 23456789 Пример задачи
Решить
Введите неравенство в график, например. грамм. y Пример задачи
Тираж
Количество решаемых неравенств: 23456789 Пример задачи
Решить
Наших пользователей:
Это программное обеспечение для алгебры обладает исключительными возможностями для индивидуальных пользователей. Предлагая помощь с домашним заданием по алгебре, он также заставляет ученика изучать основы математики. Часть программы «Репетитор по алгебре» предоставляет простые для понимания объяснения каждого шага решения задачи по алгебре.
Брайан Джонсон, Вирджиния
Я использовал ваше программное обеспечение, чтобы подготовиться к экзамену по алгебре. Мне очень нравится пошаговый процесс решения и объяснения.
Ричард Пенн, Германия.
Как только я подумал, что не могу найти программу для выполнения этой работы, я обнаружил, что Алгебратор, и мои задачи по алгебре исчезли! Спасибо.
Кэтлин Беккер, Пенсильвания
Студенты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь. Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?

Поисковые фразы, использованные на 31.01.2011:
простое математическое радикальное выражение
балансировочные уравнения, рабочий лист четвертого класса
произвольная алгебра 2 упражнения
GLENCOE ALGEBRA ONE: ИНТЕГРАЦИЯ, ПРИЛОЖЕНИЯ, ПОДКЛЮЧЕНИЯ лист ответов
вопросы по математике + множители + множители
самый сложный вопрос по математике для пятого класса
бесплатное программное обеспечение для алгебры Платона
преобразовать% в десятичное
задачи слова наклона и пересечения по оси Y
упражнения по алгебре Прентис Холла 1 ответы
Найти корень куба на графике TI-83
образец предварительного экзамена по алгебре prentice hall
упрощение экспоненциальных выражений
Уроки функции квадратного корня
Рабочий лист одновременных квадратных уравнений
Калькулятор одновременных спусков
вопросы с несколькими вариантами ответов для обратных функций
easy learn maths 10 лет
преобразовать дробь
PowerPoint
алгебра I, glencoe
что такое шкала в математике
ti-83 plus калькулятор скачать
Порядок операций перед алгеброй рабочий лист
обзоры программ для репетиторов по алгебре
решение глава 8 учет затрат
онлайн-калькулятор для решения задач с дробями
решить мои трехчленные задачи
преобразовать фракцию смеси
уравнение с дробными коэффициентами
предварительная алгебра Холта ответы
алгебра бесплатные онлайн задачи до 10 лет начальная школа
Учебники по математике для восьмого класса тройные цифры
первообразный решатель
алгебра 2 бесплатно
техасские графические калькуляторы онлайн
100% в виде десятичной дроби
коэффициент ti 83
учебное пособие по алгебре гленко 1
сложнейшая задача алгебры в мире
онлайн-программа расчета ограничений
Алгебра Холта 2 [справка]
бакалавриат алгебра решение Лэнга
смешанные числа в десятичные рабочие листы
Контрольная работа с ответами для 10 класса
Математические задачи стебля-листа 6-го класса ключевые объяснения
визуальная алгебра
глава 2 тест по математике прентис холл
Книга Фрали по алгебре
справка по алгебре + рабочие задачи
онлайн-викторина по поиску энного термина
Учебное пособие по свободной алгебре 2
Печатный лист экспонентов до алгебры
Инструкции по продвижению в столбик для шестиклассников
какой тип математики используется в азиатском искусстве симметрии?
подстановки для однородных дифференциальных уравнений
Уроки математики для использования с Western Expansion
рабочие листы по приравнению
бесплатные рабочие листы для упрощения выражений
освоение физики answer hack
пять методов факторинга + математика 10 класс
тесты по алгебре glencoe
бесплатный порядок операций распечатки игр
правило Excel для преобразования футов в метры
Калькулятор десятичных и смешанных чисел
как сделать масштабные коэффициенты
функция erfi fortran
решатель задач алгебры
Калькулятор квадратичного разложения
Рабочий лист предварительной алгебры
распечатать элементарные уроки по пропорциям и пропорциям
базовая алгебра
Таблица значений триггеров
«Комплексные рациональные выражения»
онлайн-алгебра год 8
алгебра Аддисона-Уэсли 1 выражения, уравнения и приложения для учителей
БЕСПЛАТНЫЕ РАБОЧИЕ ТАБЛИЦЫ ПО МАТЕМАТИЧЕСКИМ КЛАССАМ «УМНОЖЕНИЕ ДОПОЛНИТЕЛЬНЫХ ОБЪЯВЛЕНИЙ»
добавление отрицательных и положительных листов
Калькулятор квадратичного разложения на множители
Ti 83 коэффициент
как решить уравнение дробей
предалгебра, упрощающая выражения
выражения с переменными листами
тест по алгебре. com
Рабочие листы по предварительной алгебре
абсолютные значения примерный вопрос уровень колледжа
рабочие листы одновременных уравнений
ответы на практические задачи по калифорнийской алгебре 2 учебник
6 класс по математике как получить квадратный корень
поисковые стихи, связанные с математикой
печать умножающих многочленов оценка
8 класс математические задачи парабола
Квадратные корни и кубические корни
Чтобы найти кубический корень числа, вы хотите найти какое-то число, которое при двойном умножении на себя дает вам исходное число.Другими словами, чтобы найти кубический корень из 8, вы хотите найти число, которое при двойном умножении на само себя дает 8. Таким образом, кубический корень из 8 равен 2, потому что 2 × 2 × 2 = 8. Обратите внимание, что символ кубического корня — это знак корня с маленькой тройкой (так называемый индекс ) сверху и слева. Остальные корни определяются аналогично и идентифицируются указанным индексом. (Под квадратным корнем понимается индекс два, который обычно не записывается.) Ниже приводится список первых одиннадцати идеальных (целое число) кубических корней.
Чтобы найти квадратный корень из числа, которое не является полным квадратом, необходимо будет найти приблизительный ответ , используя процедуру, приведенную в примере.
.
Пример 1
Приблизительно.
Поскольку 6 ² = 36 и 7 ² = 49, то находится между и.
Следовательно, это значение от 6 до 7. Так как 42 находится примерно на полпути между 36 и 49, можно ожидать, что это будет примерно посередине между 6 и 7, или примерно 6.5. Чтобы проверить эту оценку, 6,5 × 6,5 = 42,25, или около 42
Квадратные корни из несовершенных квадратов можно аппроксимировать, найти в таблицах или найти с помощью калькулятора. Вы можете иметь в виду эти два:
Упрощение квадратных корней
Иногда вам придется упростить квадратных корня или записать их в простейшей форме. В долях может быть уменьшено до. В квадратных корнях можно упростить до.
Есть два основных метода упростить извлечение квадратного корня.
Метод 1: Разложите число под двумя множителями, один из которых представляет собой наибольший возможный полный квадрат. (Совершенные квадраты: 1, 4, 9, 16, 25, 36, 49,…)
Метод 2: Полностью разложите число под множителями на простые множители, а затем упростите, выведя все множители попарно.
Пример 2
Упростить.
В примере
, самый большой идеальный квадрат легко увидеть, и метод 1, вероятно, является более быстрым методом.
Пример 3
Упростить.
В примере
, не так очевидно, что наибольший идеальный квадрат равен 144, поэтому метод 2, вероятно, является более быстрым.
Многие квадратные корни нельзя упростить, потому что они уже представлены в простейшей форме, например, и.
Калькулятор алгебры с квадратными корнями
Калькулятор алгебры с квадратными корнями
Нет, это не части растений в форме кубов! Квадратные корни противоположны квадратным числам. Вот пара примеров: квадрат 3 равен 9 (3 x 3), поэтому квадратный корень 9 равен 3. Квадрат 8 равен 64 (8 x 8), поэтому квадратный корень 64 равен 8. Все числа имеют их собственный квадратный корень. Но большинство из них не так просто решить, как приведенные выше примеры.
С помощью этого калькулятора легко найти корни любого уравнения. Просто введите свою математику в предоставленное текстовое поле, нажмите кнопку вычислить, чтобы найти решение. Корни квадратных уравнений могут быть действительными, комплексными или нулевыми.Комплексный корень означает, что решение имеет как действительную, так и мнимую части вида.
Квадратные корни — это специализированная форма нашего калькулятора общих корней. «Обратите внимание, что любое положительное действительное число имеет два квадратных корня, один положительный и один отрицательный. Например, квадратные корни из 9 равны -3 и +3, поскольку (-3) 2 = (+3) 2 = 9.
Квадратный корень — описание, расположение, дизайн и история символа с сайта Symbols. com
Игра основана на следующих общих математических стандартах: CCSS8.EE.2 Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x2 = p и x3 = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких полных квадратов и кубические корни из маленьких идеальных кубов. Знайте, что √2 иррационально.
Квадратный корень из числа, вставленного пользователем, можно легко найти с помощью онлайн-калькулятора квадратного корня. Квадратные корни — это функция, противоположная возведению числа в квадрат. Напомним, возведение числа в квадрат означает умножение этого числа два раза само на себя.
квадратный корень из 42 составляет примерно 6,48 в калькуляторе алгебры, который вы можете вычислить с помощью: sqrt (42)
Алгебра вещественных чисел — алгебра вещественных чисел — коммутативный закон для сложения, ассоциативный закон для сложения и многое другое; Римские цифры — римские цифры представляют собой комбинации из семи букв; Квадраты, кубики и корни — числа — квадраты, кубы, квадратные корни и кубические корни; Тригонометрические функции — синус, косинус и тангенс — естественный тригонометрический . ..
Как настроить 4,8 vortec
На Yay Math Роберт Ахдут, основатель Yay Math, покажет вам некоторые функции квадратного корня и некоторые неравенства.Он начинает с задачи y = x². Затем он делает набросок с двумя пересекающимися линиями в форме буквы t. Проблема иллюстрируется изогнутой U-образной формой, нижняя часть U опирается на горизонтальную полосу, которая представляет x, а центр занимает вертикальную линию. Вертикальная полоса представляет … Калькулятор «Квадратный корень» автоматически вычисляет квадратный корень числа. Чтобы использовать калькулятор, введите слева положительное действительное число, затем нажмите Sq.
Какая тектоническая граница связана с мегапространственными разломами_
На уроках алгебры вам нужно будет развить практические знания о квадратных корнях.Квадратные корни — это числа, которые при умножении сами на себя равны числу под знаком квадратного корня. Например, sqrt (9) равно 3, так как 3 * 3 равно 9. Вы должны запомнить значения квадратных корней, по крайней мере, до 100.
Найдите онлайн-репетиторов по алгебре или онлайн-репетиторов по математике за пару кликов. Зарегистрируйтесь бесплатно, чтобы получить доступ к другим ресурсам по алгебре, например. Ресурсы Wyzant содержат блоги, видео, уроки и многое другое по алгебре и более чем 250 другим предметам.
21 июля 2011 г. · Поскольку в знаменателе стоит квадратный корень, нам нужно умножить его на квадратный корень из выражения, которое даст нам идеальный квадрат под квадратным корнем в знаменателе.2 = n $$$) с заданной точностью.
Best pse bow 2019
Онлайн-калькулятор корней многочлена находит корни любого многочлена и строит график полученного многочлена. Этот онлайн-калькулятор находит корни заданного многочлена. Для полиномов степени меньше или равной 4 возвращается точное значение любых корней (нулей) полинома.
Математические решения для средней школы — Калькулятор радикальных уравнений Радикальные уравнения — это уравнения, включающие радикалы любого порядка. Мы покажем примеры квадратных корней; выше …
Занятия в классе Desmos … Загрузка … … На главную> Математика> Темы по математике> Квадратные корни> Добавление квадратного корня При сложении квадратных корней важно помнить, что основания двух терминов должны совпадать для того, чтобы они были добавлены. Чтобы объединить их, мы складываем или вычитаем коэффициенты вместе.
Расписание отправки iphone
a + bi, где ‘i’ — квадратный корень из минус единицы. НЕ вводите букву «i» ни в одно из полей.Комплексное число, такое как 3 + 5i, будет введено как a = 3 bi = 5. Для комплексного числа, такого как 7 + i, вы должны ввести a = 7 bi = 1.
Определение квадрата значения и нахождение квадратного корня из этого значения — совершенно противоположные задачи. Когда мы возводим значение в квадрат, мы умножаем это значение на само значение. Если вы хотите определить квадратный корень из значения, вы пытаетесь найти, какое количество, умноженное само на себя, даст ваше исходное значение.
Положительные числа имеют два квадратных корня; положительный (называемый главным квадратным корнем) и отрицательный.Если вас не попросят ввести отрицательный квадратный корень, вы можете просто дать основной квадратный корень. Изучая с детьми квадраты и квадратные корни, подчеркивайте, что каждый процесс противоположен другому. Другими словами, отменяется … Калькулятор интегралов. Вычисляйте интегралы онлайн — с помощью шагов и графиков! Введите функцию, которую хотите интегрировать в Калькулятор интегралов. Пропустите часть «f (x) =»! Калькулятор интегралов покажет вам графическую версию введенного вами текста во время ввода.
Как перезагрузить брандмауэр cisco asa
Sofsource.com предоставляет интересный и полезный материал по квадратным корням с калькулятором дробей, матрицам и уравнениям с факторизацией и другим математическим предметам. В любое время, когда вам нужна помощь не только по мономам, но и по точкам, Sofsource.com, без сомнения, идеальный сайт для просмотра!
Калькулятор косинусов. Калькулятор тригонометрического косинуса .. Калькулятор косинуса. Чтобы вычислить cos (x) на калькуляторе: Введите входной угол.В поле со списком выберите тип угла: градусы (°) или радианы (рад).
Калькулятор квадратного корня для устранения проблем с расчетами. Если вам дано a * a = x, тогда a — квадратный корень из x, а x — квадрат из a. От конструкции до алгебры и природы — квадратные корни играют важную роль во всех сферах жизни. Однако их важность не означает, что поиск квадрата … Предалгебра, алгебра, предварительное исчисление, исчисление, математика линейной алгебры помогают. Пошаговые пояснения к вашим математическим решениям.Возможность сфотографировать вашу математическую задачу с помощью приложения. Разбивка шагов и подэтапов для каждого решения. Доступно онлайн 24/7 (даже в 3 часа ночи). Отменить подписку в любое время; никаких обязательств
Opengd77 github
Итак, квадратный корень из 20, который я люблю упрощать, — это думать о нем как о двух квадратных корнях, умноженных вместе. И я могу сказать, что 20 равно 10 умноженным на 2, но я не знаю ни одного из этих квадратных корней в виде целого числа, но я могу записать его как квадратный корень из 4 умноженный на квадратный корень из 5.Квадратный корень из 4 равен 2.
Калькулятор квадратного корня — это инструмент, используемый для нахождения квадратного и квадратного корня из заданного числа. Таблицы умножения до алгебры алгебра геометрия матрица вероятность и статистика ссуды и ипотечные проценты инвестиционные кредит и дебет прибыль и убыток валюта …
Привет, ребята, я бы очень ценил некоторую поддержку с калькулятором квадратного корня, на котором я действительно застрял . У меня было много проблем с ответами на вопросы, основанные на калькуляторе квадратного корня, но с тех пор, как я купил это программное обеспечение, математика стала чем-то вроде…В этом руководстве. посмотрим, как получить квадратный корень из числа в java. Получить квадратный корень из числа в java очень просто. Вы можете просто использовать метод sqrt () Math для вычисления квадратного корня из числа.
Загрузка драйвера аудиоинтерфейса
Калькулятор квадратного корня — щелкните значок на калькуляторе для получения квадратного корня или кубического корня и добавьте свои числа в формулу, которая отображается в бежевой области. Онлайн-калькулятор графиков — это также бесплатный онлайн-калькулятор для построения графиков уравнений алгебры и т. Д.
Не удалось зарегистрировать гибридный агент
Инструкции по использованию навеса на территории Северо-Запада
Форма соглашения об опеке над детьми NC
Как правильно поднимать тяжести для наращивания мышечной массы
Bootloop после установки twrp
Aurob неактивные ингредиенты
Freightliner cascadia код неисправности chs 216
Snapchat черный экран с белой линией
расширение магазина Glock 33
Predator 708cc стартер
Мяч выбрасывается вверх из верхней части здание разумно
Data lengkap keluaran cambodia togeli
Как изменить imei samsung a20
Медицинское руководство по ролевой игре
Сестры амебы видео резюмируют реальные жизненные сценарии ферментов
Отключение от перенапряжения gfci
Razer viper Ultimate Disconnect
Gunwerks 6.
5 prc brass review
Pua безработица вход в систему tn application
Виртуальный рабочий стол черный экран Steam vr
Практика содержания b урок 1 наземные биомы ответ ключ
Xtream ui форумы
2003 chevy trailblazer задний продольный рычаг крепления рамы ремонт
паевые инвестиционные фонды Best Fidelity
Бесплатные рабочие листы квадратного корня (PDF и html)
Вы здесь: Главная → Рабочие листы → Квадратные корни
На этой странице вы найдете неограниченное количество печатных листов для квадратных корней, включая рабочие листы только для квадратных корней (класс 7) или листы с квадратными корнями и других операций (классы 8-10).Параметры включают в себя диапазон корневого выражения, ограничение квадратных корней только точными квадратами, размер шрифта, рабочее пространство, форматы PDF или html и многое другое.
Если вы хотите, чтобы ответ был целым числом, выберите «полные квадраты», в результате чего подкоренное выражение будет совершенным квадратом (1, 4, 9, 16, 25 и т. Д.). Если вы решите разрешить использование несовершенных квадратов, ответ обычно представляет собой бесконечное десятичное число, округленное до определенного количества цифр.
Параметр «Только упрощать, без ответов в виде десятичных дробей» заставляет НЕ давать ответ в виде округленной десятичной дроби, но вместо этого ответ упрощается, если это возможно, и квадратный корень остается в ответе, если его нельзя упростить.Например, ответ √28 будет дан в упрощенной форме как 2√7. Эта опция полезна для курсов алгебры 1 и 2.
Вы также можете создавать рабочие листы, которые помимо извлечения квадратного корня включают в себя еще одну или две другие операции.

Основные инструкции для рабочих листов
Каждый рабочий лист генерируется случайным образом и поэтому уникален. Ключ ответа генерируется автоматически и помещается на вторую страницу файла.
Вы можете создавать рабочие листы либо в формате html, либо в формате PDF — и то, и другое легко распечатать. Чтобы получить рабочий лист PDF, просто нажмите кнопку с названием « Создать PDF » или « Создать рабочий лист PDF ». Чтобы получить рабочий лист в формате html, нажмите кнопку « Просмотреть в браузере » или « Сделать рабочий лист html ». Это имеет то преимущество, что вы можете сохранить рабочий лист прямо из браузера (выберите «Файл» → «Сохранить»), а затем отредактировать его в Word или другом текстовом редакторе.
Иногда созданный рабочий лист не совсем то, что вам нужно.Просто попробуйте еще раз! Чтобы получить другой рабочий лист с теми же параметрами:
Формат PDF: вернитесь на эту страницу и снова нажмите кнопку.
Формат Html: просто обновите страницу рабочего листа в окне браузера.
Готовые листы квадратного корня

Генератор
Используйте генератор для создания настраиваемых листов для вычисления квадратного корня.

Ключ к учебным пособиям по алгебре
Key to Algebra предлагает уникальный, проверенный способ познакомить студентов с алгеброй. Новые концепции объясняются простым языком, а примеры легко следовать. Задачи со словами связывают алгебру с знакомыми ситуациями, помогая учащимся понять абстрактные концепции. Учащиеся развивают понимание, интуитивно решая уравнения и неравенства, прежде чем будут представлены формальные решения. Студенты начинают изучение алгебры с книг 1–4, используя только целые числа. Книги 5-7 вводят рациональные числа и выражения. Книги 8-10 расширяют охват действительной системы счисления.
=> Узнать больше
Сложение и вычитание сурдов — Surds — Высшее — Edexcel — GCSE Maths Revision — Edexcel
Правило для сложения и вычитания сурдов состоит в том, что числа внутри квадратных корней должны совпадать с .
Пример
1xk5kwfxgos.0.0.0.1:0.1.0.$0.$1.$2″> \ [5 \ sqrt {2} — 3 \ sqrt {2} = 2 \ sqrt {2} \]
Это похоже на сбор одинаковых терминов в выражении.
\ (4 \ sqrt {2} + 3 \ sqrt {3} \) нельзя сложить, поскольку числа внутри квадратных корней не совпадают.
Вопрос
По возможности упростите следующие данные:
\ [2 \ sqrt {3} + 6 \ sqrt {3} \]
\ [8 \ sqrt {3} + 3 \ sqrt { 2} \]
\ [2 \ sqrt {5} + 9 \ sqrt {5} \]
1xk5kwfxgos.0.0.0.1:0.1.0.$0.$1.$5.2″> Показать ответ
\ [8 \ sqrt {3} \]
Невозможно складывать как числа внутри квадратные корни разные.
\ [11 \ sqrt {5} \]
Может потребоваться сначала упростить один или несколько сегментов в выражении, прежде чем добавлять или вычитать их.
Пример
\ [\ sqrt {12} + \ sqrt {27} \]
\ (12 = 4 \ times 3 \), поэтому \ (\ sqrt {12} = \ sqrt {(4 \ times 3) } = 2 \ sqrt {3} \)
1xk5kwfxgos.0.0.0.1:0.1.0.$0.$2.$3″> \ (27 = 9 \ times 3 \), поэтому \ (\ sqrt {27} = \ sqrt {(9 \ times 3)} = 3 \ sqrt {3} \)
\ [\ sqrt {12} + \ sqrt {27} = 2 \ sqrt {3} + 3 \ sqrt {3} = 5 \ sqrt {3} \]
Вопрос
Вычтите эти остатки:
\ [\ sqrt {12} — \ sqrt {27} \]
\ [\ sqrt {48} — \ sqrt {12} \]
Показать ответ
$2.$5.3.$0″>
\ [\ sqrt {( 4 \ times 3)} — \ sqrt {(9 \ times 3)} = 2 \ sqrt {3} — 3 \ sqrt {3} = — \ sqrt {3} \]
\ [\ sqrt {(16 \ times 3)} — \ sqrt {(4 \ times 3)} = 4 \ sqrt {3} — 2 \ sqrt {3} = 2 \ sqrt {3} \]
Вопрос
Найдите точный периметр этой формы.
Показать ответ
\ [2 \ sqrt {2} + 2 \ sqrt {2} + 3 \ sqrt {3} + 3 \ sqrt {3} = 4 \ sqrt {2} + 6 \ sqrt {3 } ~ \ text {cm} \]
Как вычислить квадратный корень в Excel (используя простые формулы)
Удивительно, как вы можете найти несколько способов сделать то же самое в Excel. В конце концов, существует так много потрясающих функций и возможностей.
Действительно простая и часто используемая задача — вычислить квадратный корень в Excel.
И, как я уже сказал, в Excel есть несколько способов сделать это (формулы, VBA, Power Query).
В этом уроке я покажу вам различные способы вычисления квадратного корня в Excel (и вы можете выбрать любой метод, который вам больше нравится).
Но прежде чем я перейду к тому, как это вычислить, позвольте мне быстро рассказать о том, что такое квадратный корень (не стесняйтесь переходить к следующему разделу, если я стану слишком проповедовать).
Что такое квадратный корень?
Когда вы умножаете число (скажем, X) на само себя, вы получаете значение (скажем, Y).
Здесь X — квадратный корень из Y.
Например, 10, умноженное на 10, равно 100.
Здесь 10 — квадратный корень из 100.
Вот и все! Это просто. Но посчитать это не так-то просто.
Например, если я прошу вас вычислить квадратный корень из 50, я уверен, что вы не сможете вычислить его в уме (если вы не математический гений).
Вот подробная статья в Википедии на случай, если вам интересно узнать о ней больше.
В этом уроке я покажу вам несколько способов (обещаю простые) для вычисления квадратного корня в Excel .
Итак, приступим!
Вычислить квадратный корень с помощью функции SQRT
Да, в Excel есть специальная функция, цель существования которой — дать вам квадратный корень.
Функция SQRT принимает один единственный аргумент (может быть числом или ссылкой на число) и возвращает квадратный корень из этого числа.
Чтобы вычислить квадратный корень из 100 в Excel, вы можете использовать следующую формулу:
= КОРЕНЬ (100)
Приведенная выше формула даст вам 10, что является квадратным корнем из 100.
Вы также можете использовать ссылку на ячейку в функции SQRT, как показано ниже:
Примечание. Другой результат здесь может быть -10, но формула возвращает только положительное значение.
Хотя эта функция отлично работает с положительными числами, если вы дадите ей отрицательное число, она вернет ошибку # ЧИСЛО.
Это понятно, поскольку в математике отрицательное число не имеет квадратного корня. Даже если число отрицательное, если вы умножите его само на себя, результат будет положительным.
Но если вам все еще нужен квадратный корень из отрицательного числа (при условии, что он был положительным), вам может потребоваться сначала преобразовать отрицательное число в положительное, а затем найти квадратный корень из него. Например, если вы хотите получить квадратный корень из -100, вы можете использовать функцию SQRT с функцией ABS:
= SQRT (ABS (-100))
Функция ABS дает вам абсолютное значение и игнорирует отрицательный знак.
Примечание. В Excel есть еще две функции, связанные с квадратным корнем:
SQRTPI — Эта функция возвращает квадратный корень из числа, умноженного на константу Pi (π)
IMSQRT — Эта функция возвращает квадратный корень из комплексного числа
Вычислить квадратный корень с помощью экспоненциального оператора
Другой способ вычисления квадратного корня (или кубического корня или N-го корня) в Excel — использование экспоненциального оператора. 1/2 даст два разных результата. Это связано с тем, что экспоненциальный оператор получает предпочтение перед делением и вычисляется первым. Использование скобок решает эту проблему.
Вычислить квадратный корень с помощью функции СТЕПЕНЬ
Другой простой способ вычислить квадратный корень в Excel (или кубический корень, или корень N-й степени) — использовать функцию СТЕПЕНЬ.
Ниже приведен синтаксис функции СТЕПЕНЬ:
= МОЩНОСТЬ (число, мощность)
Требуется два аргумента:
базовое число (может быть любым действительным числом)
степень / экспонента, к которой это основание число увеличивается
В отличие от функции КОРЕНЬ, вы можете использовать функцию СТЕПЕНЬ для вычисления корней (например, квадратного корня или кубического корня) или степени (например, квадрат или куб) числа.
Ниже приведена формула, которая даст вам квадратный корень из 100 в Excel:
= МОЩНОСТЬ (100,1 / 2)
или
= МОЩНОСТЬ (100, 0,5)
Если вы хотите кубический корень, вы можете использовать следующую формулу:
= МОЩНОСТЬ (100,1 / 3)
И аналогично, если вам нужен квадрат числа, вы можете использовать ту же формулу с соответствующим вторым аргументом.
= POWER (100,2)
Если вы используете отрицательное число в функции POWER, оно вернет ошибку #NUM.
Получение квадратного корня с помощью Power Query
Хотя приведенные выше формулы очень быстрые, и, если вы работаете с большим количеством данных, и это то, что вам нужно делать довольно часто, вы также можете рассмотреть возможность использования Power Query.
Этот метод больше подходит, когда у вас есть большой набор данных, где вы хотите вычислить квадратный корень из значений в столбце, и вы получаете новый набор данных каждый день / неделю / месяц / квартал. Использование Power Query минимизирует усилия, поскольку вы можете просто подключить новые данные и обновить запрос, и он даст вам результат.
Для этого примера я буду использовать простой набор данных, как показано ниже, где мне нужно вычислить квадратный корень для значений в столбце B.
Ниже приведены шаги для вычисления квадратного корня с помощью Power Query в Excel:
Выберите любую ячейку в наборе данных
Щелкните вкладку «Вставить»
Щелкните значок «Таблица» (он находится в группе «Таблицы»). Это откроет диалоговое окно Create Table.
Проверьте диапазон и отметьте опцию «Моя таблица имеет заголовки».Щелкните ОК. Это преобразует табличные данные в таблицу Excel.
Щелкните вкладку «Данные».
В группе «Получить и преобразовать» щелкните параметр «Из таблицы / диапазона». Откроется редактор Power Query.
В редакторе запросов щелкните заголовок столбца.
Перейдите на вкладку «Преобразование»
В группе «Число» щелкните научную опцию.
Щелкните «Квадратный корень». Это мгновенно изменит значения в выбранном столбце и даст вам квадратные корни из исходных чисел.
Щелкните вкладку «Файл».
Нажмите «Закрыть и загрузить».
Приведенные выше шаги позволят создать новый рабочий лист в книге Excel и вставить таблицу из Power Query. Эта новая таблица будет иметь квадратные корни исходных табличных данных.
Если у вас есть отрицательные значения в ячейках, вы получите ошибку #NUM в итоговой таблице.
Несмотря на то, что для того, чтобы заставить это работать с Power Query, требуется несколько шагов, потрясающее преимущество Power Query заключается в том, что теперь вы можете просто обновлять и получать новые результаты, когда вы получаете новые данные.
Например, если вы теперь получаете новые данные в следующем месяце, вам нужно просто скопировать и вставить эти данные в таблицу, которую мы создали (на шаге 4), перейти в любую ячейку в таблице, полученной из Power Query, справа — нажмите и нажмите «Обновить».
Итак, хотя для того, чтобы сделать это в первый раз, требуется несколько щелчков мышью, после установки вы легко преобразуете новые данные с помощью простого обновления.
Помимо квадратного корня, вы также можете использовать функцию Power в Power Query, чтобы получить кубический корень или корень N-й степени (или получить квадрат или куб чисел).
Вставка символа квадратного корня (√) в Excel
Хотя это немного не по теме, я подумал, что я также дам вам знать, как вставить квадратный корень в Excel.
Это может быть полезно, если вы хотите отобразить значение рядом с символом квадратного корня и квадратным корнем из него. Что-то вроде того, что показано ниже.
И точно так же, как у нас есть разные формулы для вычисления значения квадратного корня в Excel, у нас также есть несколько методов для вставки символа квадратного корня.
Вставить символ квадратного корня с помощью ярлыка
Если вы используете цифровую клавиатуру, вот сочетание клавиш для вставки символа квадратного корня:
ALT + 251
Удерживая клавишу ALT, нажмите цифровые клавиши 2,5 и 1 на цифровой клавиатуре. Теперь, когда вы оставите ключи, будет вставлен символ квадратного корня.
Вставить символ квадратного корня с формулой
Вы также можете использовать формулу для получения символа квадратного корня в Excel.
Это может быть полезно, когда имеется столбец значений, и вы хотите быстро добавить ко всем ним символ квадратного корня.
Чтобы получить символ квадратного корня, вы можете использовать следующую формулу:
= UNICHAR (8730)
Поскольку это формула, вы также можете комбинировать ее с другими формулами или ссылками на ячейки. Например, если у вас есть столбец значений и вы хотите добавить символ квадратного корня ко всем этим значениям, вы можете использовать формулу, как показано ниже:
= UNICHAR (8730) & A1
Примечание. хотите получить квадратный корень пару раз, вы можете получить его один раз, используя сочетание клавиш или формулу, а затем просто скопируйте и вставьте его.
Вставить символ квадратного корня путем изменения пользовательского числового формата
И, наконец, третий способ добавить символ квадратного корня — это изменить форматирование ячейки таким образом, чтобы оно отображалось всякий раз, когда вы вводите что-либо в ячейку.
Ниже Ниже приведены шаги по изменению форматирования ячеек для автоматического добавления символа квадратного корня:
Выберите ячейки, в которых должен автоматически отображаться символ квадратного корня
Удерживая клавишу Ctrl, нажмите клавишу 1.Откроется диалоговое окно «Форматирование ячеек».