Сложение вычитание умножение деление дробей: Приведение дробей к общему знаменателю онлайн

Сложение, вычитание, умножение и деление десятичных дробей

Сложение и вычитание десятичных дробей аналогично сложению и вычитанию натуральных чисел, но с определенными условиями.

Правило. Сложение и вычитание десятичных дробей производится по разрядам целой и дробной части как натуральных чисел.

При письменном сложении и вычитании десятичных дробей запятая, отделяющая целую часть от дробной, должна находиться у слагаемых и суммы или у уменьшаемого, вычитаемого и разности в одном столбце (запятая под запятой от записи условия до конца вычисления).

Примеры.

Сложение и вычитание десятичных дробей в строку:

243,625 + 24,026 = 200 + 40 + 3 + 0,6 + 0,02 + 0,005 + 20 + 4 + 0,02 + 0,006 = 200 + (40 + 20) + (3 + 4)+ 0,6 + (0,02 + 0,02) + (0,005 + 0,006) = 200 + 60 + 7 + 0,6 + 0,04 + 0,011 = 200 + 60 + 7 + 0,6 + (0,04 + 0,01) + 0,001 = 200 + 60 + 7 + 0,6 + 0,05 + 0,001 = 267,651

843,217 — 700,628 = (800 — 700) + 40 + 3 + (0,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + (1,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + (0,11 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,09 + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + (0,017 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + 0,009 = 142,589

Сложение и вычитание десятичных дробей в столбик:

Сложение десятичных дробей требует верхней дополнительной строки для записи чисел, когда сумма разряда переходит через десяток. Вычитание десятичных дробей требует верхней дополнительной строки для того, чтобы отметить разряд, в котором одалживается 1.

Если справа от слагаемого или уменьшаемого не хватает разрядов дробной части, то справа в дробной части можно дописывать столько нулей (увеличивать разрядность дробной части), сколько разрядов в другом слагаемом или уменьшаемом.

Умножение десятичных дробей производится так же, как и умножение натуральных чисел, по тем же правилам, но в произведении ставится запятая по сумме разрядов множителей в дробной части, считая справа налево (сумма разрядов множителей — это количество разрядов после запятой у множителей, вместе взятых).

Пример:

При умножении десятичных дробей в столбик первая справа значащая цифра подписывается под первой справа значащей цифрой, как и в натуральных числах:

Запись умножения десятичных дробей в столбик:

Запись деления десятичных дробей в столбик:

Подчеркнутые знаки — это знаки, за которые переносится запятая, потому что делитель должен быть целым числом.

Правило. При делении дробей делитель десятичной дроби увеличивается на столько разрядов, сколько разрядов в дробной его части. Чтобы дробь не изменилась, на столько же разрядов увеличивается и делимое (в делимом и делителе запятая переносится на одно и то же число знаков). Запятая ставится в частном на том этапе деления, когда целая часть дроби разделена.

Для десятичных дробей, как и для натуральных чисел, сохраняется правило: на ноль десятичную дробь делить нельзя!

Запись опубликована в рубрике Математика с метками вычитание, деление, десятичная, дробь, сложение, умножение. Добавьте в закладки постоянную ссылку.

Десятичные дроби сложение и вычитание, умножение и деление

Обыкновенную дробь, знаменатель которой равен 10, 100, 1000, … называют десятичной дробью.

Например, , , . Десятичные дроби изучают в 5 классе, объяснение простое – это дробь, знаменатель которой число , где . Удивительно, но любое число можно представить в виде десятичной дроби.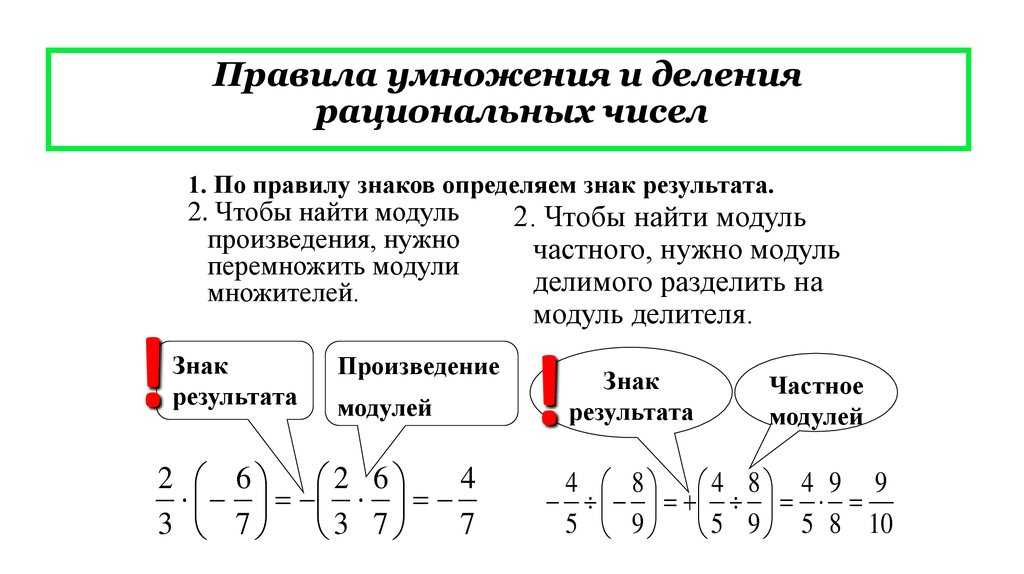 Например, число 6 – это десятичная дробь 6,0, а дробь .

Содержание

Представление любого числа в виде десятичной дроби

Попробуем представить в виде десятичной дроби дробь , для этого разделим 5 на 4, получим . Подберем к числу 4 целый множитель, чтобы при умножении получить 10 или 100. Подходит число 25. Умножим числитель и знаменатель дроби на 25, дробь не изменится, а мы получим – десятичную дробь. Однако, этот метод получения десятичной дроби довольно сложный, на практике часто пользуются простым делением в столбик:

Видно, что когда заканчивается целая часть и мы сносим 0, в этот момент мы ставим запятую и отделяем целую часть десятичной дроби от дробной. Все остальные полученные числа при делении будут записываться после запятой.

Обозначение целой и дробной части

Итак, как же выглядит десятичная дробь? Она состоит из двух частей – целой и дробной.

Десятичная дробь целая и дробная части

В дробной части есть свои разряды:

Представленную дробь можно прочитать так “одна целая двести пятьдесят шесть тысяч семьсот восемьдесят девять миллионных”.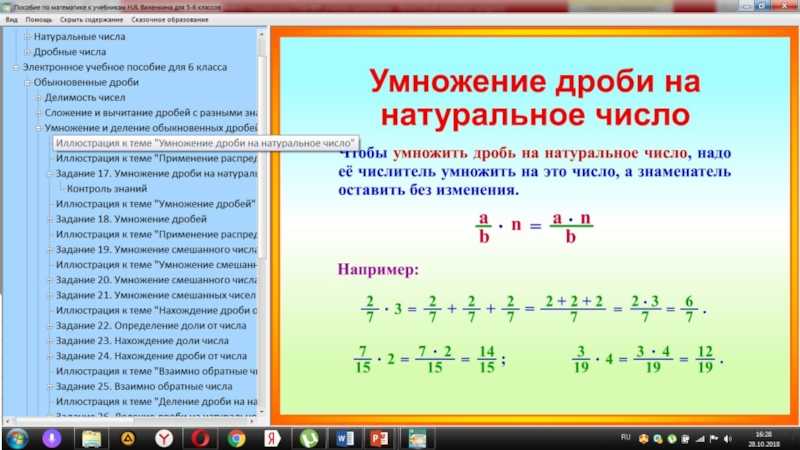

Например, дробь 1,25 читаем так: “одна целая двадцать пять сотых”.

Число 2, 354 читается так: “две целых триста пятьдесят четыре тысячных”.

Сложение и вычитание десятичных дробей

Запомни!

При сложении (вычитании) десятичных дробей числа записывают так, чтобы одинаковые разряды были записаны один под другим, а запятая под запятой и складывают (вычитают) как натуральные числа.

Например, сложение двух десятичных дробей 0,23567 и 2,56890 запишется так:

Сложение десятичных дробей

А вычитание десятичных дробей можно записать так:

Вычитание десятичных дробей

Умножение десятичных дробей

Чтобы умножить одну десятичную дробь на другую, надо выполнить умножение, не обращая внимания на запятые, и в полученном произведении отделить справа запятой столько цифр, сколько их стоит после запятой в обоих множителях вместе.

Например,

Умножение десятичных дробей

Деление десятичных дробей

Деление десятичных дробей можно проводить несколькими способами, в зависимости от того, какие числа мы делим. Давайте их рассмотрим.

1. Пусть нам нужно разделить десятичную дробь на целое число. Тогда делим а это число сначала целую часть, а потом и дробную часть. Например, разделим 6,86 на 2. Разделим на 2 сначала целую часть числа, а потом и его дробную часть – сначала десятые доли, а потом и сотые. Получим: 6,86:2=3,43.
2. Если целая часть числа не делится нацело, то, значит, мы займем число у дробной части, а целая соответственно будет равна 0. Как при обычном делении чисел. Например, разделим 1,25 на 5. При делении числа 125 на 5 мы получили бы 25, но в данном случае у нас нет целой части, поэтому мы запишем 0,25.
3. Разделим десятичную дробь на десятичную дробь. Например, 6,05 разделим на 0,55. Умножим обе дроби на 100 и получается, что нам нужно разделить 605 на 55. При делении находим частное – 11.  Если нам нужно, например, разделить 1,25 на 1,5, то можно умножить обе дроби на 10, чтобы избавиться от запятой в делителе. И получается, что мы делим десятичную дробь 12,5 на 15. Можно поделить в столбик. Однако, если вас смущает десятичная дробь в делимом, то можно сразу смело умножить обе дроби на 100. Делить станет немного труднее, ввиду больших чисел, но зато психологически комфортнее, пока вы хорошо не освоили эту тему. Получим следующее: Деление десятичных дробей

Правило деления числа на десятичную дробь.

Чтобы разделить число на десятичную дробь, нужно в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, а потом выполнить деление на натуральное число.

Умножение и деление десятичной дроби на 10, 100, 1000 и так далее

При умножении (делении) десятичной дроби на 10, 100, 1000 и так далее достаточно перенести запятую вправо (влево) на столько цифр, сколько нулей во множителе (делителе). Например, если нужно умножить 2,456 на 100, то мы переносим запятую на два знака (в 100 два нуля) вправо (увеличиваем число, ведь оно выросло в 100 раз), 2,456 ·100=245,6. Если нужно разделить число 2,456 на 100, то переносим запятую на два знака влево (уменьшаем число, ведь оно уменьшилось в 100 раз), 2,456:100=0,02456.

Читайте еще по математике:

Как складывать, вычитать, умножать и делить дроби

Введение

Прежде чем вы сможете освоить более сложные понятия алгебры и геометрии, вам необходимо сначала освоить все математические функции, связанные с дробями. В этой статье мы рассмотрим, как складывать, вычитать, умножать и делить две дроби, а также дробь и целое число. Мы также введем сложные дроби вместе с методами их упрощения. Прежде чем продолжить, убедитесь, что вы полностью понимаете четыре основных математических операции: сложение, вычитание, умножение и деление.

Ключевые термины

o Общий знаменатель

o Взаимная

o Комплексная фракция

Цели

O Изучение

o Понимание, как интерпретировать дробь, которые включают отрицательные числа

o Признание и упростить комплексы

Теперь, когда мы разработали прочную основу относительно того, что такое дроби, а также о некоторых различных типах дробей, мы можем теперь перейти к применению основных арифметических операций (сложение, вычитание, умножение и деление) к дробям.

Сложение и вычитание

В случаях, когда речь идет о простых числах, сложение и вычитание дробей выполняется достаточно просто. Например, добавление одной трети и одной трети, очевидно, дает нам две трети. Точно так же три пятых минус две пятых — это одна пятая. Первый случай проиллюстрирован ниже.

А как быть с такими случаями, как половина плюс одна треть?

Обратите внимание, что складывать (вычитать) дроби с одинаковым знаменателем очень просто — мы просто складываем (вычитаем) числители и делим на тот же знаменатель. Мы уже должны знать, что можем написать эквивалентные дроби, которые имеют разные числители и знаменатели. Таким образом, если мы просто преобразуем одну или обе дроби, которые мы складываем или вычитаем, в эквивалентные дроби с тем же знаменателем, то мы можем складывать дроби простым способом, описанным выше. Затем, при необходимости, мы можем уменьшить результат до минимальных значений.

Задача при сложении и вычитании дробей состоит в том, чтобы найти общий знаменатель . Самый простой способ найти общий знаменатель — просто умножить два существующих знаменателя, а затем соответствующим образом преобразовать числители, чтобы получить эквивалентные дроби. Хотя этот подход концептуально прост, он может быть математически сложным, когда знаменатели велики. Тем не менее, давайте попробуем этот подход для иллюстрации. Обратите внимание на упомянутое выше дополнение.

Общий знаменатель равен 6 (или 23), потому что мы можем умножить числитель и знаменатель на 3, чтобы получить , и мы можем умножить числитель и знаменатель на 2, чтобы получить . Добавление тогда просто.

Практическая задача: Подсчитайте результат в каждом случае.

а. б. в.

Решение: В каждом случае найдите общий знаменатель и преобразуйте члены в эквивалентные дроби с этим знаменателем. Для каждого случая дается один возможный общий знаменатель. Сумма (разность) дробей есть сумма (разность) числителей над общим знаменателем. Если применимо, уменьшите результат до самых низких значений.

а. Общий знаменатель: 21

б. Общий знаменатель: 8

Хотите узнать больше? Почему бы не пройти онлайн-курс Pre-Algebra?

в. Общий знаменатель: 45

Умножение и деление

Умножение и деление дробей в некоторых отношениях проще, чем их сложение и вычитание. Допустим, мы хотим умножить на . Интуитивно ответ довольно очевиден: половина половины — это четверть (или одна четвертая). Например, если у вас есть 50 центов (полдоллара) и вы хотите умножить их на половину, то вы получите 25 центов (четверть доллара).

Чтобы умножить две дроби, просто умножьте числители и умножьте знаменатели, чтобы получить произведение. В некоторых случаях товар уже будет в наименьших условиях; в других вам может потребоваться уменьшить его до самых низких значений. Например, произведение и будет следующим:

При умножении дроби на целое число обратите внимание, что любое целое число — это просто дробь с целым числом в числителе и 1 в знаменателе.

Например,

Практическая задача : Рассчитайте следующие произведения.

а. б. в.

Решение : В каждом случае произведение равно произведению числителей на произведение знаменателей. Если один из множителей является целым числом, рассматривайте его как дробь, имеющую целое число в числителе и 1 в знаменателе. Сократите продукт до самых низких условий, если это применимо.

а.

б.

в.

Теперь рассмотрим случай деления. Допустим, мы хотим разделить на . Интуитивно ответ равен 2. Например, 25 центов (четверть доллара) могут дважды превратиться в 50 центов (полдоллара).

 

Обратите внимание, что если бы мы перевернули второй множитель так, чтобы числитель стал знаменателем, а знаменатель стал числителем, а также изменили операцию деления на умножение, мы получили бы тот же результат.

На самом деле это удобный способ деления дробей. Деление на дробь равносильно умножению на 9.0004 обратное этой дроби. Обратное — это просто «перевернутая» дробь. Так, например, обратная величина равна (или ).

Как и при умножении дробей, помните, что целое число также можно записать в виде дроби. Так, например, обратное число 6 равно . Поэтому мы можем делить дроби на целые числа так же, как и на другие дроби. Кроме того, обратите внимание, что произведение дроби и ее обратной всегда равно 1. Рассмотрим пример ниже.

В свете того, как мы определили деление и умножение, мы можем дать более строгое обоснование нашего метода вычисления эквивалентных дробей. Обратите внимание, что число 1 можно записать как любое другое число, разделенное само на себя. Например,

Таким образом, процесс нахождения эквивалентных дробей есть не что иное, как умножение данной дроби на 1! Рассмотрим пример ниже.

Практическая задача : Вычислите следующие частные.

а. б. в.

Решение : В каждом случае умножьте делимое на обратную величину делителя. Сократите продукт до самых низких условий, если это применимо.

а.

б.

г.

  

Дроби и отрицательные числа

Поскольку дроби — это не что иное, как представление деления, у нас уже есть инструменты, необходимые для понимания роли отрицательных чисел в дробях. Напомним, что произведение (или частное) двух отрицательных или двух положительных чисел положительно, а произведение (или частное) одного отрицательного числа и одного положительного числа отрицательно. Итак, рассмотрим на примере дроби ; мы рассмотрим каждый возможный случай.

В первом случае (числитель и знаменатель имеют одинаковый знак) результатом является положительное число. Во втором случае (числитель и знаменатель имеют противоположные знаки) результатом является отрицательное число. Таким образом, во втором случае мы можем иногда просто ставить знак минус рядом со всей дробью, а не рядом с числителем или знаменателем. Тем не менее, обратите внимание, что все три представления равны, и в некоторых ситуациях одно может быть более полезным, чем другое.

Сложные дроби

Напомним, что дробь — это просто способ выражения деления двух чисел (где числитель — это делимое, а знаменатель — делитель). Поскольку мы можем делить дроби, мы можем также выразить это деление как «дробь дробей» или сложных дробей. Ниже приведен пример сложной дроби. Обратите внимание, что для ясности дроби в числителе и знаменателе сложной дроби показаны «наклонными» — однако это изменение не означает никакой математической разницы.

Такие дроби можно и часто нужно упрощать. Для этого мы можем воспользоваться одним из нескольких подходов. Напомним, что мы можем найти эквивалентную дробь, умножив числитель и знаменатель на одно и то же число. Таким образом, один из подходов состоит в том, чтобы умножить как числитель, так и знаменатель сложной дроби на произведение знаменателей простых дробей, как показано ниже.

В качестве альтернативы мы можем умножить и числитель, и знаменатель сложной дроби на обратную величину ее знаменателя. Поскольку знаменатель становится равным 1, результатом является просто значение числителя.

Другой способ взглянуть на этот последний подход состоит в том, что мы просто выполняем деление:

В зависимости от конкретной ситуации один подход может быть проще другого; однако все они одинаково приемлемы.

Практическая задача : Упростите следующие сложные дроби.

а. б. в.

Решение : Одним из возможных способов упрощения сложных дробей является умножение дроби в числителе на обратную дробь в знаменателе. Если применимо, уменьшите результат до самых низких значений. В случае части c обратите внимание, что обратная величина 5 равна и что частное (или произведение) положительного числа, деленного (умноженного) на отрицательное число, является отрицательным числом.

а.

б.

г.

Если у вас все еще возникают проблемы с дробями, вы также можете прочитать эту статью здесь: Как сделать дроби простым способом.

Сложение, вычитание, умножение, деление дробей

Предоставил:

Диего Чт, 27 января 2022 г., 06:10 UTC

В этом PDF-файле мы будем выполнять различные арифметические операции над дробями. Дробь представляет собой часть целого или, в более общем смысле, любое количество равных частей. Дробь описывает, сколько имеется частей определенного размера, например, половина, восемь пятых, три четверти.

1. Сложение дробей
Адаптировано с сайта MathisFun.com
Чтобы сложить дроби, нужно выполнить 3 простых шага:
 Шаг 1: Убедитесь, что нижние числа (знаменатели) совпадают
 Шаг 2: Сложите верхние числа (числители). Поместите ответ над знаменателем.
 Шаг 3: Упростите дробь (при необходимости).
Пример 1:
1 1
+
4 4
Шаг 1. Нижние числа (знаменатели) уже совпадают. Сразу переходите к шагу 2.
Шаг 2. Сложите верхние числа и поставьте ответ над тем же знаменателем:
1 1 1+1 2
+ = =
4 4 4 4
Шаг 3. Упростите дробь:
2 1
=
4 2
В виде рисунка это выглядит так:
1 1 2 1
/4 + /4 = /4 = /2
(Если вы не уверены в последнем шаге, см. Эквивалентные дроби.)

2. Пример 2:
1 1
+
3 6
Шаг 1: Нижние числа разные. Видите, как кусочки разного размера?
1 1
/3 + /6 = ?
Нам нужно сделать их одинаковыми, прежде чем мы сможем продолжить, потому что мы не можем добавлять их таким образом.
Число «6» в два раза больше числа «3», поэтому, чтобы нижние числа были одинаковыми, мы можем
умножить верхнюю и нижнюю части первой дроби на 2, например:
× 2
1 2
=
3 6
× 2
Важно: вы умножаете верхнее и нижнее число на одинаковую величину, чтобы значение дроби
оставалось одинаковым
Теперь дроби имеют одинаковое нижнее число («6 «), и наш вопрос выглядит так:

3. 2 1
/6 + /6
Нижние числа теперь одинаковы, поэтому мы можем перейти к шагу 2.
Шаг 2: Сложите верхние числа и поместите их над тем же знаменателем:
2 1 2+1 3
+ = =
6 6 6 6
В виде рисунка это выглядит так:
2 1 3
/6 + /6 = /6
Шаг 3: Упростите дробь:
3 1
=
6 2
В виде рисунка весь ответ выглядит так:

4. 2 1 3 1
/6 + /6 = /6 = /2
Стихотворение, которое поможет вам запомнить
♫ «Если ваша цель — сложение или вычитание,
Нижние числа должны совпадать! Но то же самое нужно применить и к верхнему,
♫ «И не забудьте упростить,
Прежде чем пора прощаться»
Пример 3:
1 1
+
3 5
Опять же, нижние числа разные ( ломтики разного размера)!
1 1
/3 + /5 = ?
Но давайте попробуем разделить их на меньшие размеры, каждый из которых будет одинаковым:

5. 5 3
/15 + /15
Первая дробь: умножив верх и низ на 5, мы получили 5/15 :
× 5
1 5
=
3 15
× 5
Вторая дробь: умножив сверху и снизу по 3, мы получили 3/15 :
×3
1 3
=
5 15
×3
Нижние числа теперь одинаковы, поэтому мы можем продолжить и добавить верхние числа:
5 3 8
/15 + /15 = /15

6. Сложение дробей с разными знаменателями
Но что, если знаменатели (нижние числа) не совпадают? Как в этом примере:
3 1
/8 + /4 = ?
+ =
Надо как-то сделать знаменатели одинаковыми.
В данном случае это легко, потому что мы знаем, что 1/4 равно 2/8:
3 2 5
/8 + /8 = /8
+ =
В этом примере было легко вычислить знаменатели то же самое, но это может быть сложнее … поэтому вам
может потребоваться использовать любой из этих методов (нахождение наименьшего общего знаменателя или нахождение
Общий знаменатель), чтобы сделать их одинаковыми (они оба работают, используйте любой из них).
Вычитание дробей
Существует 3 простых шага для вычитания дробей
 Шаг 1. Убедитесь, что нижние числа (знаменатели) совпадают
 Шаг 2. Вычтите верхние числа (числители). Поместите ответ над тем же знаменателем
.
 Шаг 3. Упростите дробь.

7. Пример 1:
3 1
–
4 4
Шаг 1. Нижние числа уже совпадают. Сразу переходите к шагу 2.
Шаг 2. Вычтите верхние числа и поставьте ответ над тем же знаменателем:
3 1 3–1 2
– = =
4 4 4 4
Шаг 3. Упростите дробь:
2 1
=
4 2
Пример 2:
1 1
–
2 6
Шаг 1. Нижние числа разные. Видите, как кусочки разного размера? Нам нужно
сделайте их одинаковыми, прежде чем мы сможем продолжить, потому что мы не можем вычесть их следующим образом:
1 1
/2 — /6 = ?

8. Чтобы нижние числа были одинаковыми, умножьте верхнюю и нижнюю части первой дроби (1/2) на 3
следующим образом:
× 3
1 3
=
2 6
× 3
А теперь наш вопрос выглядит так :
3 1
/6 — /6
Нижние числа (знаменатели) совпадают, поэтому мы можем перейти к шагу 2.
Шаг 2. Вычесть верхние числа и поставить ответ над тем же знаменателем:
3 1 3–1 2
– = =
6 6 6 6
На картинке это выглядит так:
3 1 2
/6 — /6 = /6

9. Шаг 3. Упростите дробь:
2 1
=
6
Сложение и вычитание смешанных дробей
Краткое определение: смешанная дробь представляет собой целое число
и дробь вместе,
, например 1 3/4.
1 3/4
(одна и три четверти)
Чтобы их было легко складывать и вычитать, просто сначала преобразуйте их в неправильные дроби:
Краткое определение: неправильная дробь имеет
верхнее число, большее или равное
нижний номер,
, например, 7/4 или 4/3
7
/4 (это «тяжелый верх»)
(семь четвертей или семь четвертей)
Добавление смешанных дробей
Я считаю, что это лучший способ сложения смешанных дробей :
 преобразовать их в неправильные дроби
 затем сложить их (используя сложение дробей)
 затем преобразовать обратно в смешанные дроби:
Пример: Сколько будет 2 3/4 + 3 1/2 ?

10. Преобразовать в неправильные дроби:
2 3/4 = 11/4
3 1/2 = 7/2
Общий знаменатель 4:
11
/4 остается как 11/4
7
/2 становится 14/4
(путем умножения верхнего и нижнего на 2)
Теперь добавим:
11
/4 + 14/4 = 25 /4
Преобразовать обратно в смешанные дроби:
25
/4 = 6 1/4
Когда у вас будет больше опыта, вы сможете сделать это быстрее, например:
Пример: Что такое 3 5/8 + 1 3/4
Преобразовать их в неправильные дроби:
3 5/8 = 29/8
1 3/4 = 7/4
Сделайте тот же знаменатель: 7/4 станет 14/8 (путем умножения верхнего и нижнего на 2)
И прибавьте:
/8 + 14/8 = 43/8 = 5 3/8
Вычитание смешанных дробей
Просто следуйте тому же методу, но вместо прибавления вычтите:
Пример: чему равно 15 3/4 — 8 5/ 6 ?

11. Преобразование в неправильные дроби:
15 3/4 = 63/4
8 5/6 = 53/6
Общий знаменатель числа 12:
63
/4 становится 189/12
53
/6 становится 106/12
Теперь вычитаем :
189
/12 — 106/12 = 83/12
Преобразование обратно в смешанные дроби:
83
/12 = 6 11/12

12. Умножение дробей
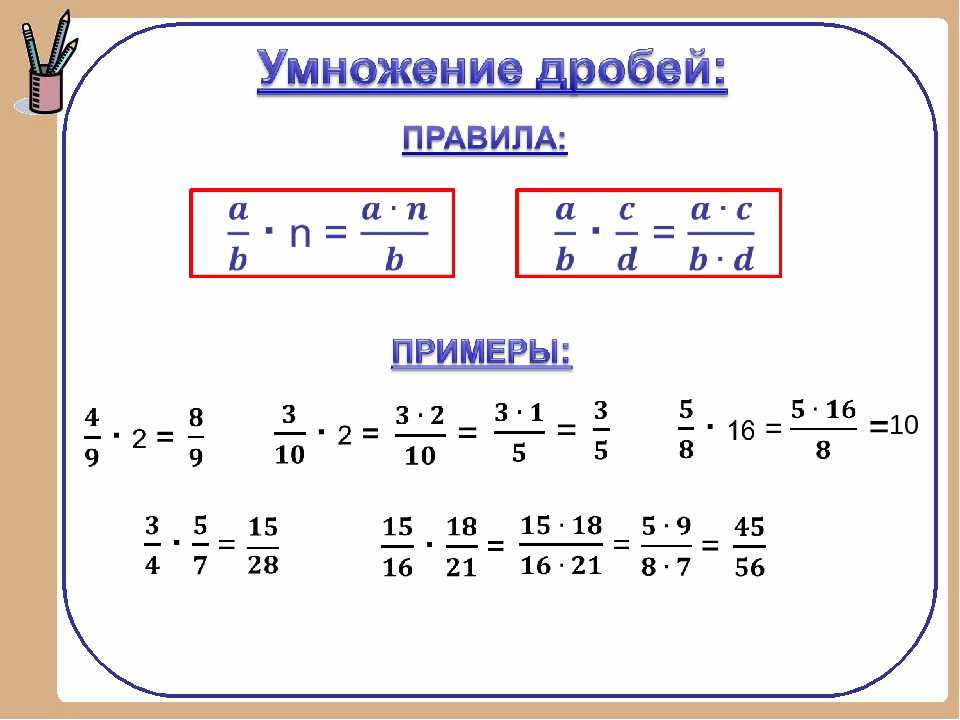
Умножьте верхние части, умножьте нижние.
Есть 3 простых шага, чтобы умножить дроби
1. Умножьте верхние числа (числители).
2. Умножьте нижние числа (знаменатели).
3. При необходимости упростите дробь.
Пример 1
1 2
×
2 5
Шаг 1. Умножьте верхние числа:
1 2 1×2 2
× = =
2 5
Шаг 2. Умножьте нижние числа:
1 2 1×2 2
× = =
2 5 2×5 10
Шаг 3. Упростите дробь:
2 1
=
10 5
Пример 2
1 9
×
3 16

13. Шаг 1. Умножьте верхние числа:
1 9 1×9 9
× = =
3 16
Шаг 2. Умножьте нижние числа:
1 9 1×9 9
× = =
3 16 3 × 16 48
Шаг 3. Упростите дробь:
9 3
=
48 16
Стихотворение, которое поможет вам запомнить
♫ «Умножение дробей: не проблема ,
Верх умножить на верх над низом умножить на низ.» ♫
Умножение смешанных дробей
(«Смешанные дроби» также называются «смешанными числами»)
Чтобы умножить смешанные дроби:
1. преобразовать в неправильные дроби
2. Умножить дроби
3. преобразовать результат обратно в смешанные дроби
Пример: Что такое 13/8 × 3 ?
Подумайте о пицце.
1 3/8 — это 1 пицца и 3 восьмых другой пиццы.

14. Во-первых, преобразуйте смешанную дробь (1 3/8) в неправильную дробь (11/8):
Разрежьте всю пиццу на восьмые и сколько у вас всего
восьмых?
1 партия из 8 плюс 3 восьмых = 8+3 = 11 восьмых.
Теперь умножьте это на 3:
1 3/8 × 3 = 11/8 × 3/1 = 33/8
У вас 33 восьмых.
И, наконец, преобразовать в смешанную дробь (только потому, что исходная дробь была в таком виде):

15. 33 восьмых — это 4 целых пиццы (4 × 8 = 32) и 1 восьмая
осталась.
А вот как это выглядит в одной строке:
1 3/8 × 3 = 11/8 × 3/1 = 33/8 = 4 1/8
Другой пример: что такое 11/2 x 21/5?
Выполните действия, описанные выше:
1. Преобразуйте в неправильные дроби
2. Умножьте дроби
3. преобразовать результат обратно в смешанные дроби
Шаг за шагом это:

16. Преобразовать обе дроби в неправильные
1 1/2 × 2 1/5 = 3/2 × 11/5
Умножить дроби (умножить верхние числа на нижние):
3
/2 × 11/5 = (3 × 11)/(2 × 5) = 33/10
Преобразование в смешанное число
33
/10 = 3 3/10
Если вы умны, вы можете сделать все это в одной строке, например:
1 1/2 × 2 1/5 = 3/2 × 11/5 = 33/10 = 3 3/10
Еще один пример: что такое 31/4 x 31/3?
Преобразовать оба числа в неправильные дроби
3 1/4 × 3 1/3 = 13/4 × 10/3
13
/4 × 10/3 = 130/12
Преобразовать в смешанное число (и упростить):
130
/12 = 10 10/12 = 10 5/6
Еще раз, здесь в одной строке:
3 1/4 × 3 1/3 = 13/4 × 10/3 = 130/12 = 10 10/ 12 = 10 5/6
У этого есть отрицания: сколько будет -15/9 × -21/7 ?
Преобразование смешанных дробей в неправильные:
1 5/9 = 9/9 + 5/9 = 14/9
2 1/7 = 14/7 + 1/7 = 15/7

17. Затем умножьте неправильные дроби (Примечание: отрицательное умножение на отрицательное дает нам положительное значение):
-14
/9 × -15/7 = -14х-15 / 9х7 = 210/63
Затем я решил упростить следующее, сначала на 7 (потому что я заметил, что 21 и 63 кратны
7 ), затем снова на 3 (но я мог бы сделать это за один шаг, разделив на 21):
210
/63 = 30/9 = 10/3
Наконец, преобразовать в смешанную дробь (потому что это был стиль вопрос):
10
/3 = (9+1)/3 = 9/3 + 1/3 = 3 1/3

18. Разделение дробей
Переверните вторую дробь вверх ногами и просто умножьте.
Есть 3 простых шага для деления дробей:
Шаг 1. Переверните вторую дробь (ту, на которую вы хотите разделить) вверх ногами
(теперь это обратное число).
Шаг 2. Умножьте первую дробь на обратную
Шаг 3. Упростите дробь (при необходимости)
Пример 1
1 1
÷
2 6
Шаг 1. Переверните вторую дробь (она станет обратной) :
1 6
становится
6 1
Шаг 2. Умножьте первую дробь на обратную:
1 6 1×6 6
× = =
2 1 2×1 2
Шаг 3. Упростите дробь:
6
= 3
2
Имеет ли это смысл?
1 1
Действительно ли ÷ равно 3 ?
2 6
Вы можете изменить вопрос типа «Сколько будет 20 разделить на 5?» в «Сколько пятерок вписывается в 20?»
Точно так же наш дробный вопрос может стать:

19. 1 1 1 1
÷ Сколько в ?
2 6 6 2
Теперь посмотрите на пиццу ниже… сколько «1/6 кусочков» помещается в «1/2 кусочка»?
Сколько в ? Ответ: 3
1 1
Итак, теперь вы видите, что ÷ =3 действительно имеет смысл!
2 6
Пример 2
1 1
÷
8 4
Шаг 1. Переверните вторую дробь (обратное число):
1 4
станет
4 1
Шаг 2. Умножьте первую дробь на это обратное число:
1 4 1×4 4
× = =
8 1 8×1 8
Шаг 3. Упростите дробь:
4 1
=
8 2
И это все, что вам нужно сделать.