Калькулятор сокращения дробей
Примеры сокращения дробей
| Сократим дробь | 64 | |
| 88 |
Способ 1
1. Найдем наибольший общий делитель числителя и знаменателя (вы можете воспользоваться калькулятором нахождения НОД)
НОД (64 ; 88) = 8
2. Разделим числитель и знаменатель на их НОД
64 : 8 = 8
88 : 8 = 11
3. Подставим результаты деления в числитель и знаменатель. Получаем дробь
Способ 2
1. Разложим числитель и знаменатель на простые множители (вы можете воспользоваться калькулятором разложения числа на простые множители)
64 = 2∙2∙2∙2∙2∙2
88 = 2∙2∙2∙11
2. Представим числитель и знаменатель дроби в виде их разложения на простые множители
| 2∙2∙2∙2∙2∙2 | ||
| 2∙2∙2∙11 |
3. Вычеркнем те множители, которые повторяются и в числителе и в знаменателе
| 2∙2∙2∙2∙2∙2 | = | |
| 2∙2∙2∙11 |
| 2∙2∙2∙2∙2∙2 | ||
| 2∙2∙2∙11 |
4. Оставшиеся множители запишем в числитель и знаменатель. Если в числителе или знаменателе остаются несколько множителей, то нужно перемножить их между собой.
| 2∙2∙2∙2∙2∙2 | = | |
| 2∙2∙2∙11 |
| 2∙2∙2∙2∙2∙2 | = | |
| 2∙2∙2∙11 |
| Сократим дробь 6 | 20 | |
| 48 |
Способ 1
1. Найдем наибольший общий делитель числителя и знаменателя (вы можете воспользоваться калькулятором нахождения НОД)
НОД (20 ; 48) = 4
2. Разделим числитель и знаменатель на их НОД
20 : 4 = 5
48 : 4 = 12
3. Подставим результаты деления в числитель и знаменатель. Получаем дробь
Способ 2
1. Разложим числитель и знаменатель на простые множители (вы можете воспользоваться калькулятором разложения числа на простые множители)
20 = 2∙2∙5
48 = 2∙2∙2∙2∙3
2. Представим числитель и знаменатель дроби в виде их разложения на простые множители
| 6 | 2∙2∙5 | |
| 2∙2∙2∙2∙3 |
3. Вычеркнем те множители, которые повторяются и в числителе и в знаменателе
| 6 | 2∙2∙5 | = |
| 2∙2∙2∙2∙3 |
| 6 | 2∙2∙5 | |
| 2∙2∙2∙2∙3 |
4. Оставшиеся множители запишем в числитель и знаменатель. Если в числителе или знаменателе остаются несколько множителей, то нужно перемножить их между собой.
| 6 | 2∙2∙5 | = |
| 2∙2∙2∙2∙3 |
| 6 | 2∙2∙5 | = |
| 2∙2∙2∙2∙3 |
| Сократим дробь | 246 | |
| 764 |
Способ 1
1. Найдем наибольший общий делитель числителя и знаменателя (вы можете воспользоваться калькулятором нахождения НОД)
НОД (246 ; 764) = 2
2. Разделим числитель и знаменатель на их НОД
246 : 2 = 123
764 : 2 = 382
3. Подставим результаты деления в числитель и знаменатель. Получаем дробь
Способ 2
1. Разложим числитель и знаменатель на простые множители (вы можете воспользоваться калькулятором разложения числа на простые множители)
246 = 2∙3∙41
764 = 2∙2∙191
2. Представим числитель и знаменатель дроби в виде их разложения на простые множители
3. Вычеркнем те множители, которые повторяются и в числителе и в знаменателе
4. Оставшиеся множители запишем в числитель и знаменатель. Если в числителе или знаменателе остаются несколько множителей, то нужно перемножить их между собой.
Перейти в калькулятор
matematika-club.ru
Калькулятор онлайн — Сокращение дробей
С помощью данного калькулятора онлайн вы можете сократить обыкновенную, неправильную, смешанную дробь.
Если числитель больше знаменателя, то после сокращения дроби выделяется целая часть.
Калькулятор онлайн для сокращения дробей не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс нахождения решения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода дробей, рекомендуем с ними ознакомиться.
Правила ввода дробей
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: \( -\frac{2}{3} \)
Целая часть отделяется от дроби знаком амперсанд:
Ввод: -5&8/3
Результат: \( -5\frac{8}{3} \)
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Обыкновенные дроби. Деление с остатком
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель. Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток. В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление. Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\( m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a : m}{b : m} \)
Это свойство называют основным свойством дроби.
Два последних преобразования называют сокращением дроби.
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю.
Правильные и неправильные дроби. Смешанные числа
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными.
Например:
\( 5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \( \frac{2}{3} \) — дробная часть.
Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\( \large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
\( \large \frac{a}{b} : n = \frac{a}{bn} \)
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \). Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть.
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
С помощью букв это правило записывается так:
\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \). Эту дробь называют обратной дроби \( \frac{2}{3} \).
Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как \( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.
Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.
www.math-solution.ru
Сокращение обыкновенных дробей. Онлайн калькулятор
Сокращение дроби – это замена данной дроби, на равную ей дробь, у которой числитель и знаменатель меньше, чем у данной дроби.
Сокращение дроби выполняется путём деления числителя и знаменателя на одно и то же число.
Сократить можно только такую дробь, у которой члены имеют какой-нибудь общий делитель, помимо единицы.
Например, дробь можно сократить, а дробь нельзя, так как у первой дроби числитель и знаменатель имеют общие делители помимо единицы (это 2 и 4), а числитель и знаменатель второй дроби не имеют никакого общего делителя, кроме единицы.
Дробь, которую нельзя сократить, называется несократимой дробью.
Сокращение можно произвести или постепенно или сразу, выполнив деление членов дроби на НОД.
При постепенном сокращении дробь сокращают более одного раза. Сначала подбирают наименьший общий делитель (кроме единицы) для обоих членов дроби и сокращают дробь на него. Полученную после сокращения дробь, если можно, сокращают таким же путём снова и такое постепенное сокращение продолжают до тех пор, пока не получится несократимая дробь.
Пример: сократить дробь . Сначала сократим эту дробь, используя постепенное сокращение:
В результате мы получили несократимую дробь . Тот же результат мы получим, если найдём НОД чисел 24 и 432. НОД (24, 432) = 24, сократив члены дроби на 24, получим:
Если числитель дроби делится на знаменатель, то дробь равна частному от деления числителя на знаменатель:
Калькулятор сокращения дробей
Данный калькулятор поможет вам выполнить сокращение обыкновенной дроби. Просто введите числитель и знаменатель и нажмите кнопку Сократить
.
naobumium.info
Калькулятор корней с решением онлайн
Корень в математике
Операция извлечения корня из числа, является обратной операцией к операции возведения в степень.
Обозначение: корень обозначается при помощи символа, который называется знаком корня. Число a, которое находится под корнем называется подкоренным выражением, а число n, расположенное слева от символа корня, называется – степенью корня.
Степень корня – должна быть выражена натуральным числом (1, 2, 3, 4, 5…), т.е. не может быть отрицательной, нулем или дробным числом.
По сути, как уже было сказано выше извлечь корень из числа а означает возведение числа a в дробную степень, числителем которой выступает степень числа a, а знаменателем – степень корня.
Следует заметить, что если степень корня равна 2, то число два как правило не пишут, а такой корень называется – квадратным.
Приведем примеры:
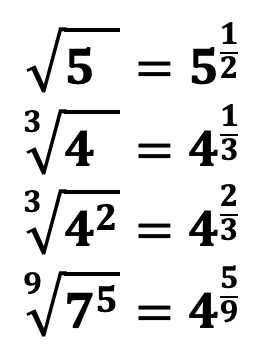
Приведем примеры извлечения корня:

Исходя из вышенаписанных примеров можно сделать вывод, что когда мы хотим извлечь корень, к примеру 2-й степени, то нам необходимо найти такое число, что при возведении во 2-ю степень мы получим подкоренное выражение. То есть под корнем всегда находится число, уже возведенное в степень равную степени корня!
Четная и нечетная степень корня
Корень нечетной степени
При извлечении корня нечетной степени из положительного числа будем всегда получать положительное число, например:
При извлечении корня нечетной степени из отрицательного числа будем всегда получать отрицательное число, например
В данном примере можно легко увидеть почему при извлечении корня нечетной степени из отрицательного числа всегда будет получаться отрицательно число. Как известно чтобы возвести число в степень необходимо его умножить само на себя в количестве показателя степени : если (-6) умножить на (-6) получится положительное число 36 (мы знаем, что при умножении двух отрицательных чисел будет получаться положительное число), затем если умножить число 36 на (-6) получим -216, так как при умножении отрицательного числа на положительное всегда будет получаться отрицательное число.
Корень четной степени
При извлечении корня четной степени из положительного числа всегда будет получать два значения с противоположенными знаками. Это связанно с тем, что если представить, к примеру функцию квадратного корня y= √x и посмотреть на ее график, то мы увидим, что каждому значению xсоответствует два значения корня, одно положительное, а другое отрицательное.
Для понимания данного факта, нет необходимости строить график, рассмотрим на примере извлечение квадратного корня из числа 4:
Квадратный корень из 4 равен 2 так как = 4 и . Проверим 2 ⋅ 2 = 4 и -2 ⋅(-2) = 4.
Приведем еще пример с четной степенью корня для положительного числа.
Корень степени 4 за числа 81 равен 3 так как = 81 и . Проверим 3 ⋅ 3 ⋅ 3 ⋅ 3 = 81 и -3 ⋅ (-3) ⋅ (-3) ⋅ (-3) = 81
Теперь рассмотрим ситуацию, когда под корнем четной степени стоит отрицательное число.
Допустим, мы ходим извлечь квадратный корень из отрицательного числа, например, √-4 теперь подумаем есть ли вообще такое число, которое при возведении в квадрат давало бы -4? Ответ – нет! Любое число при возведении в четную степень всегда будет положительным. Поэтому корня чётной степени из любого отрицательного числа не существует в области вещественных чисел, поскольку при возведении любого вещественного числа в степень с чётным показателем результатом будет неотрицательное число.
Тем не менее извлечь корень четной степени всё-таки можно, но результатом будет всегда комплексное число, например:
Арифметический и алгебраический корни
Для упрощения записи корня четной степени из положительного числа, в калькуляторах, школьных учебниках и т.д. было введено понятие арифметического корня, значение которого, представляется всегда положительным числом. Алгебраический корень в свою очередь для корня четной степени из положительного числа является полным ответом и содержит как положительные, так и отрицательные значения.
Арифметический корень – упрощенная запись корня четной степени из положительного числа, всегда положительный. Например:
Алгебраический корень – полная запись корня четной степени из положительного числа. Например:
Как упростить корень
Для того, чтобы упростить любой корень, необходимо разложить подкоренное выражение на простые множители (для разложения числа на простые множители можно воспользоваться калькулятором разложения числа на простые множители) и вынести за знак корня тот множитель, который повторяется равное степени корня число раз. Например:
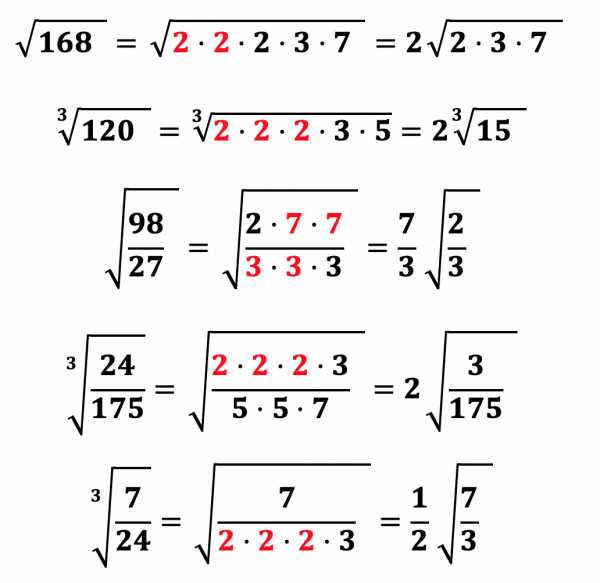
Как мы уже разобрали извлечь корень из числа а означает возведение числа a в дробную степень, числителем которой выступает степень числа a, а знаменателем – степень корня, поэтому следуя данному правилу мы легко выносим множители из под корня. Распишем предыдущие два примера еще раз:
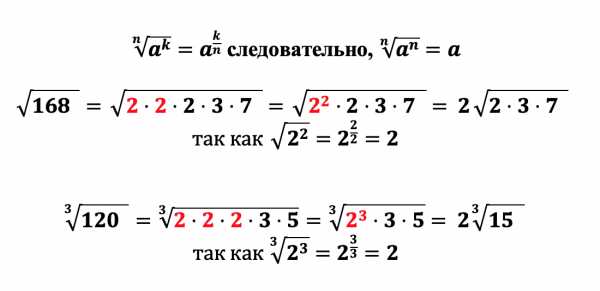
matematika-club.ru
