| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица тангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тангенс 1
Когда требуется найти тангенс 1, tg 2, tg 3, tg 4, tg 6, помогут единичная окружность и линия тангенсов.
Для начала отметим на единичной окружности углы в 1, 2, 3, 4, 5 и 6 радиан. Это можно сделать тремя способами.
1) 1 радиан — это приблизительно 57 градусов. Соответственно, через каждые 57 градусов отмечаем: 1 радиан, 2, 3…
2) 1 радиан — это угол, длина дуги которого равна радиусу окружности. В этом случае каждую следующую отметку ставим, откладывая приблизительно дугу длиной в радиус.
В этом случае каждую следующую отметку ставим, откладывая приблизительно дугу длиной в радиус.
3) если вспомнить, что п — это приближенно 3,14, и рассчитать п/2, 3п/2, 2п, а 1,2, 3,4,5 и 6 радиан — ориентируясь на эти значения.
Получаем приблизительно такой чертеж:
Если нужно сравнить, например, tg1 и tg2, этого чертежа вполне достаточно. 1 радиан — угол 1й четверти, где тангенс положителен, а 2 радиана — угол 2й четверти, где тангенс отрицателен (см. как запомнить знаки тангенса). Поэтому tg1 > tg2.
Когда требуется сравнить тангенсы одного знака, например, tg 5 и tg 6, единичной окружности недостаточно. Найти значения tg1, tg2, tg3, tg4, tg6 можно также с помощью линии тангенсов.
Линия тангенсов — это касательная к единичной окружности в точке (1;0). То есть линия тангенсов — это прямая x=1.
Если через точку О — начало отсчета- и отмеченный на единичной окружности угол в 1 радиан провести луч, то он пересечет линию тангенсов в точке, которая показывает значения tg 1. Поскольку окружность единичная, то значения 2,3,4 и т.д. получаем, откладывая на линии тангенсов длину радиуса. Соответственно, tg 1 получаем где-то посредине между 1 и 2, чуть ближе к 2. Аналогично на линии тангенсов определяем, чему равен тангенс 2, тангенс 3, тангенс 4, тангенс 5 и тангенс 6. Отсюда делаем вывод: tg5 < tg6, tg2>tg5, tg4<tg1.
Поскольку окружность единичная, то значения 2,3,4 и т.д. получаем, откладывая на линии тангенсов длину радиуса. Соответственно, tg 1 получаем где-то посредине между 1 и 2, чуть ближе к 2. Аналогично на линии тангенсов определяем, чему равен тангенс 2, тангенс 3, тангенс 4, тангенс 5 и тангенс 6. Отсюда делаем вывод: tg5 < tg6, tg2>tg5, tg4<tg1.
Конечно, все эти значения можно получить с помощью калькулятора. Но в тех случаях, когда воспользоваться калькулятором нельзя, этот способ работает.
Получать значения тангенса и сравнивать их можно также с помощью графика функции y=tg x. Но это уже другая история.
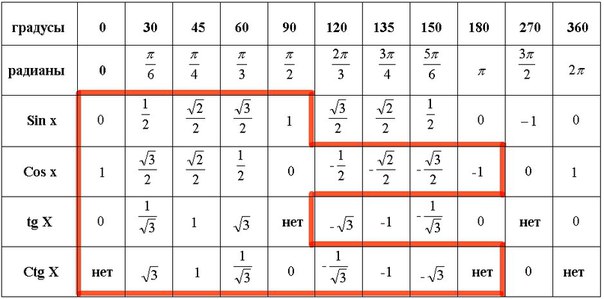
Таблица тангенсов, полная таблица значений тангенсов для студентов
Содержание:
Тангенс — равен отношению синуса к косинусу (tg(x) = Sin(x)/Cos(x)), тоесть таблицу тангенсов
можно получить просто поделив значения из
таблицы синусов на значения из
таблицы косинусов. Таблица тангенсов
применяется не часто, но так как из всех
таблиц тригонометрических функций
значения таблицы тангенсов получить сложнее всего, то эти значения как минимум надо иметь по близости. Для лучшего понимания тригонометрии советуем изучить
тригонометрические формулы. Пользуйтесь
таблицей тангенсов на здоровье.
Для лучшего понимания тригонометрии советуем изучить
тригонометрические формулы. Пользуйтесь
таблицей тангенсов на здоровье.
Таблица тангенсов 0° — 180°
|
|
|
Таблица тангенсов 180° — 360°
|
|
|
Слишком сложно?
Таблица тангенсов, таблица значений тангенсов не по зубам? Тебе ответит эксперт через 10 минут!
Функция TAN — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование
в Microsoft Excel.
Описание
Возвращает тангенс заданного угла.
Синтаксис
TAN(число)
Аргументы функции TAN описаны ниже.
Замечания
Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание (результат) | Результат |
|---|---|---|
|
=TAN(0,785) |
Тангенс 0,785 радиан (0,99920) |
0,99920 |
|
=TAN(45*ПИ()/180) |
Тангенс угла 45 градусов (1) |
1 |
|
=TAN(РАДИАНЫ(45)) |
Тангенс угла 45 градусов (1) |
1 |
Тангенс угла
В этой статье мы разберем такое понятие, как тангенс угла. Начнем с понятия прямого угла. Прямым углом называется угол равный 900. Угол в котором меньше 90 градусов — называется острым. Угол в котором больше 90 градусов — называется тупым. В развернутом угле 180 градусов.
Начнем с понятия прямого угла. Прямым углом называется угол равный 900. Угол в котором меньше 90 градусов — называется острым. Угол в котором больше 90 градусов — называется тупым. В развернутом угле 180 градусов.
Изображаем треугольник с прямым углом С , при этом противолежащая сторона будет имеет такое же обозначение (с -будет гипотенузой), аналогично поступаем и с другими углами. Сторона находящаяся противоположно от острого угла — называется катетом.
Синус и косинус находятся с помощью катета и гипотенузы, а именно:
cosA = b/c
Формула тангенса
tg A = a/b
другими словами определение тангенса — это деление противоположного катета на прилежащий
Существует ещё одна равносильная формула тангенса
tg A = sinA/cosA
расшифровывается как деление sin на cos.
Котангенс находится практически аналогично, лишь значения поменяются местами.
ctg A = cosA/sinA
Внимание! В помощь родителям и учителям гдз по математики 5 класс (http://spisaly.ru/gdz/5_klass/math). Все предложенные на сайте книги можно скачать или изучить онлайн. Перейдите по ссылке и узнайте подробнее.
Данные тригонометрические функции, значительно облегчают вычисление углов. Благодаря синусу, косинусу и тангенсу стало возможным, определение всех неизвестных углов в треугольнике, с одним известным.
Обозначения для основных углов:
тангенс 30 — 0,577
тангенс 45 — 1,000
тангенс 60 — 1,732
Существуют специальная таблица тангенсов, значения которой можно получить при помощи деления значений таблиц синуса и косинуса, но так как это достаточно трудоемкий процесс и нужна данная таблица тангенсов.
Есть очень много задач в которых у треугольника углы равны 90, 30, 60 градусам. либо 90, 45, 45 градусам. Для таких фигур лучше заучить их соотношение , что бы потом было проще.
В первом случае катет противоположный 30 градусам равняется 1/2 от гипотенузы.
Во втором случае гипотенуза превышает катет в ?2 раз.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Тангенс и котангенс. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти тангенсы и котангенсы угла, представленных как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Тангенс и котангенс − теория, примеры и решения
Определение 1. Число, равное отношению
называется тангенсом угла α и обозначается
Определение 2. Число, равное отношению
Число, равное отношению
называется котангенсом угла α и обозначается
Подробнее о синусах и косинусах посмотрите на странице Синус и косинус. Онлайн калькулятор.
Свойство A1. Область определения функции тангенс −это все действительные числа α, удовлетворяющие выражению
где Z множество целых чисел.
Действительно. Из равенства (1) следует, что cos α должен быть отличным от нуля. А это в свою очередь показывает справедливость равенства (3).
Свойство A2. Область определения функции котангенс −это все действительные числа α, удовлетворяющие выражению
где Z множество целых чисел.
Действительно. Из равенства (2) следует, что sin α должен быть отличным от нуля. А это в свою очередь показывает справедливость равенства (4).
Свойство 1. tg α и сtg α нечетные функции, т.е. для любого допустимого значения α справедливы равенства
Доказательство. Воспользуемся равенствами и (cм. на странице Синус и косинус. Онлайн калькулятор). Тогда имеем:
на странице Синус и косинус. Онлайн калькулятор). Тогда имеем:
Свойство 2. tg α и сtg α периодичные функции с основным периодом π (180°), т.е. для любого допустимого значения α справедливы равенства
или в градусах:
Доказательство. Воспользуемся тем, что или (cм. на странице Синус и косинус. Онлайн калькулятор):
или в градусах:
И вообще
или в градусах:
Использем таблицы синусов и косинусов, и построим таблицу тангенсов и котангенсов некоторых углов, учитывая уравнение (1):
Пример 1. Найти тангенс и котангенс угла равного 420°(или радиан).
Воспользуемся уравнениями (11)− (14):
или :
или :
Пример 2. Найти тангенс и котангенс угла равного -225°(или радиан).
Воспользуемся уравнениями (11)− (14):
или :
или :
Как мы уже знаем из определения синуса и косинуса sin α=y2, cos α=x2 (Рис. 1). Покажем, что tg α=AN, ctg α=KP
1). Покажем, что tg α=AN, ctg α=KP
Построим каноническое уравнение прямой, проходящей через точки и (см. статью на странице Каноническое уравнение прямой на плоскости):
Тогда учитывая, что , имеем:
или
Поскольку , , тогда
При x=1 имеем y=tg α. Т.е. tg α − это ординат точки пересечения прямых ON и NA
Выразим в (15) x через y:
Подставляя , , получим:
Взяв y=1, получим x=ctg α. Таким образом ctg α − это абсцисс точки пересечения прямых ON и KP.
Так как для функциий привычнее запись y=f(x), то вместо записей u=tg α и u=сtg α мы будем использовать записи y=tg x и y=сtg x.
График функции тангенс (
y=tg x)Построим график функции тангенс на интервале . Выберем контрольные точки:
Отметим эти точки на координатной плоскости XOY и проведем через них плавную кривую (Рис.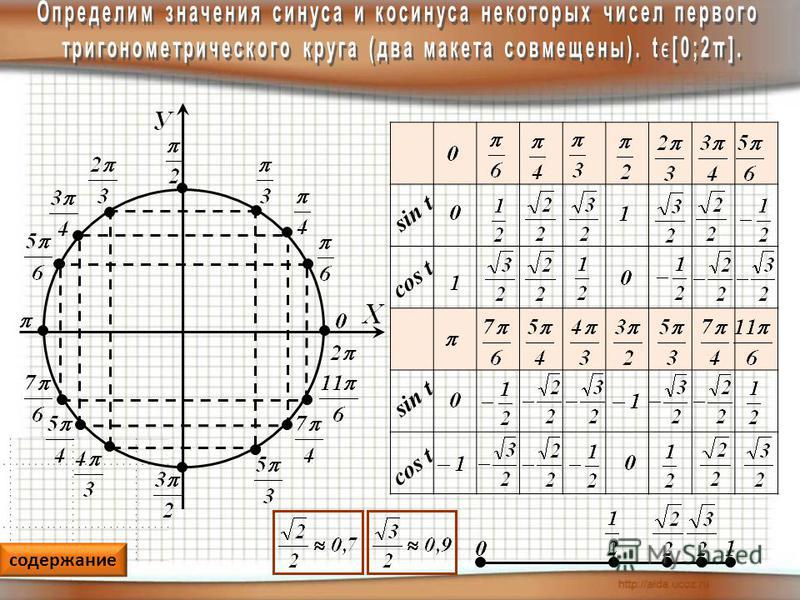 2)
2)
Учитывая свойство 1 построим симметричную к этой кривой относительно начала координат (Рис.3)
Функция тангенс периодичная (свойство 2) с основным периодом π. Тогда на графике функции тангенс, ветвь на рисунке Рис.2 повторяется бесконечное число раз от -∞ до ∞:
В точках функция имеет разрыв. Каждая прямая вида является вертикальной асимптотой графика функции.
График функции котангенс (
y=сtg x)Построим график функции котангенс на интервале [0; π). Выберем контрольные точки:
Взяв π≈3, высислим значения x, отметим эти точки на координатной плоскости XOY и проведем через них плавную кривую (Рис. 5)
Функция котангенс периодичная (свойство 2) с основным периодом π. Тогда на графике функции котангенс, ветвь на рисунке Рис.5 повторяется бесконечное число раз от -∞ до ∞:
В точках функция имеет разрыв. Каждая прямая вида является вертикальной асимптотой графика функции котангенс.
Функция тангенса: онлайн калькулятор, формулы, график
Тангенс — тригонометрическая функция, численно равная соотношению длин противолежащего и прилежащего катета. Тангенс широко используется во многих современных приложениях.
История вопроса
Тригонометрия берет свое начало в Древнем Вавилоне, когда ученые изучали свойства сторон прямоугольного треугольника. Именно тогда была сформулирована теорема, постулирующая соотношение катетов и гипотенузы, доказанная только через полторы тысячи лет самосским математиком Пифагором. Изначально использовался только синус, который рассчитывался как половина хорды окружности, описанной вокруг прямоугольного треугольника.
Тангенс появился гораздо позднее, когда перед учеными возникла задача определения длины тени, отбрасываемой объектами, стоящими перпендикулярно к поверхности земли. Тангенс был введен арабским математиком Абу-ль-Вафой в десятом веке. Восточный ученый составил специальные таблицы для определения тангенсов и котангенсов, однако это открытие так и не попало на европейский континент.
В Европе тангенсы были вновь открыты только в XIV веке: немецкий математик Иоганн Мюллер Региомонтан использовал функцию в астрономических расчетах. Термин «тангенс» произошел от латинского слова tanger, что означает «касание» и был введен в обиход в конце XVI века. Данный термин использовался для описания линии тангенсов, то есть касательной к единичной окружности. Региомонтан доказал теорему тангенсов, а также составил специальные таблицы значений функции, которые подошли как для плоской, так и для сферической геометрии.
Определение тангенса
Геометрически тангенс определяется как соотношение противолежавшего катета к прилежащему. Функция всегда рассчитывается для угла и не зависит от длин сторон. Пусть у нас есть треугольник со сторонами A, B и C, где C — гипотенуза. Тангенс угла AC будет рассчитываться как соотношение противолежащего катета B к прилежащему A или tgAC = B/A. Для угла BC тангенс рассчитывается как дробь, в числителе которой длина противолежащего углу катета A к прилежащему B, что математически записывается как tgBC = A/B. Угол AB образуется при двумя катетами, поэтому его невозможно посчитать. Катеты — стороны, образующие прямой угол, поэтому для угла в 90 градусов тангенс не существует.
Угол AB образуется при двумя катетами, поэтому его невозможно посчитать. Катеты — стороны, образующие прямой угол, поэтому для угла в 90 градусов тангенс не существует.
Помимо геометрического определения, тангенс легко выразить через другие тригонометрические функции. Так, для угла A тангенс можно выразить при помощи отношения синуса и косинуса:
tgA = sinA / cosA.
Наша программа позволяет определить численное значение тангенса для любого значения угла. Для этого достаточно выбрать в меню соответствующую функцию и ввести в ячейку «Угол» величину угла в градусах или радианах. Если необходимо найти угол по известному значению тригонометрической функции, используйте функцию арктангенса. Для этого введите значение тангенса в соответствующую ячейку, после чего калькулятор вернет вам величину угла.
Рассмотрим пару примеров
Вычисление угла
Пусть в школьной задаче задан прямоугольный треугольник со сторонами A = 5 см, B = 12 см, C = 13 см. Требуется найти величины всех углов. Итак, очевидно, что угол AB, то есть угол, образуемый двумя катетами — прямой. Это известно из самого определения катетов. Теперь мы можем найти тангенс угла BC, который численно будет равен дроби, в числителе которой противолежащий катет A, а в знаменателе — прилежащий B. Следовательно, tgBC = A/B = 5/12 = 0,416. Зная тангенс, мы легко можем вычислить соответствующий угол при помощи онлайн-калькулятора. Для это выберем в меню функцию тангенса и введем значение 0,416 в ячейку tgα. Программа мгновенно отобразит величину угла, равную 22,58 градуса. Вычислить последний угол не составит труда, так согласно постулату о сумме углов треугольника, угол AC = 180 − 90 − 22,58 = 67,42 градуса.
Итак, очевидно, что угол AB, то есть угол, образуемый двумя катетами — прямой. Это известно из самого определения катетов. Теперь мы можем найти тангенс угла BC, который численно будет равен дроби, в числителе которой противолежащий катет A, а в знаменателе — прилежащий B. Следовательно, tgBC = A/B = 5/12 = 0,416. Зная тангенс, мы легко можем вычислить соответствующий угол при помощи онлайн-калькулятора. Для это выберем в меню функцию тангенса и введем значение 0,416 в ячейку tgα. Программа мгновенно отобразит величину угла, равную 22,58 градуса. Вычислить последний угол не составит труда, так согласно постулату о сумме углов треугольника, угол AC = 180 − 90 − 22,58 = 67,42 градуса.
Вычисление тангенса
В школьных задачах чаще всего используются стандартные углы, поэтому школьникам важно знать значения основных тригонометрических функций для этих углов буквально наизусть. Давайте при помощи калькулятора определим значения тангенсов для наиболее распространенных в задачах углов:
- tg30 = 0,577;
- tg45 = 1;
- tg60 = 1,732;
- tg90 — не рассчитывается;
- tg120 = -1,732;
- tg150 = -0,577;
- tg180 = 0.

Выше мы выяснили, почему тангенс не рассчитывается для значений 90 градусов. Еще одно интересное значение — угол в 45 градусов. Почему тангенс равен 1? Ответ очевиден, ведь если в прямоугольном треугольнике один угол равен 45 градусам, то и второй имеет такую же величину. Следовательно, треугольник равнобедренный, его катеты имеют одинаковую длину, а их соотношение в любом случае будет равно 1.
Заключение
Тригонометрия — сложная наука, которая не находит практически никакого применения в повседневной жизни. Однако без тригонометрии не было бы современных технологий, поэтому специалистам прикладных наук без нее никуда. Используйте наши онлайн-калькуляторы для расчета значений тригонометрических функций.
PI = 3,141592 .
|
Как преобразовать касательные в градусы
Простое упоминание слова «тригонометрия» могло вызвать дрожь по позвоночнику, пробудив воспоминания о школьных уроках математики и таких загадочных терминах, как грех, косяк и загар, которые никогда не имели никакого смысла.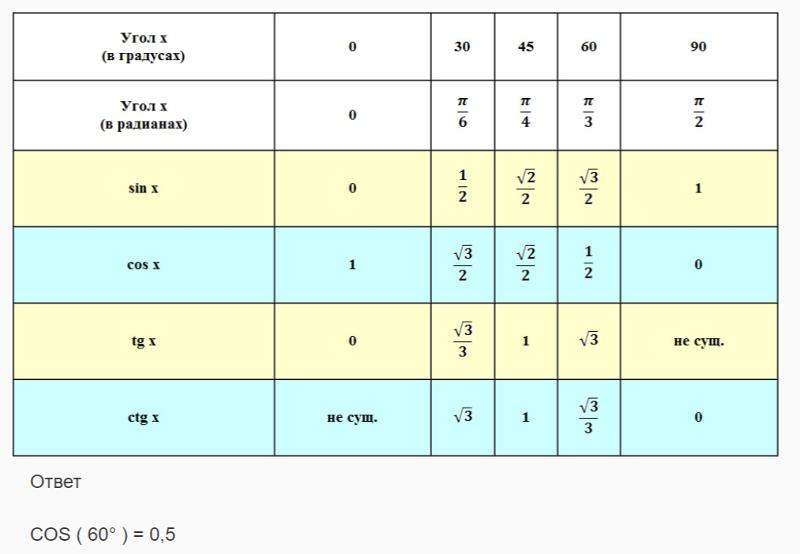 Но правда в том, что тригонометрия имеет огромное количество приложений, особенно если вы занимаетесь естественными науками или математикой в рамках непрерывного образования.Если вы не знаете, что на самом деле означает касательная или как извлечь из нее полезную информацию, научитесь преобразовывать касательные в градусы, чтобы познакомить вас с наиболее важными понятиями.
Но правда в том, что тригонометрия имеет огромное количество приложений, особенно если вы занимаетесь естественными науками или математикой в рамках непрерывного образования.Если вы не знаете, что на самом деле означает касательная или как извлечь из нее полезную информацию, научитесь преобразовывать касательные в градусы, чтобы познакомить вас с наиболее важными понятиями.
TL; DR (слишком длинный; не читал)
Для стандартного прямоугольного треугольника загар угла ( θ ) говорит вам:
Желто-коричневый ( θ ) = напротив / рядом
С противоположной и смежной вставкой по длине соответствующих сторон.
Преобразуйте касательные в градусы по формуле:
Угол в градусах = arctan (tan ( θ ))
Здесь arctan переворачивает функцию тангенса, и его можно найти на большинстве калькуляторов как tan — 1 .
Что такое касательная?
В тригонометрии тангенс угла можно найти, используя длины сторон прямоугольного треугольника, содержащего угол. Соседняя сторона находится горизонтально рядом с интересующим вас углом, а противоположная сторона стоит вертикально, напротив интересующего вас угла. Оставшаяся сторона, гипотенуза, играет определенную роль в определениях cos и sin но не загара.
Соседняя сторона находится горизонтально рядом с интересующим вас углом, а противоположная сторона стоит вертикально, напротив интересующего вас угла. Оставшаяся сторона, гипотенуза, играет определенную роль в определениях cos и sin но не загара.
Имея в виду этот общий треугольник, тангенс угла ( θ ) можно найти с помощью:
\ tan (θ) = \ frac {\ text {напротив}} {\ text {смежный}}
Здесь напротив и рядом описаны длины сторон с этими именами.Думая о гипотенузе как о наклоне, тангенс угла наклона говорит вам о подъеме наклона (то есть вертикальном изменении), деленном на длину наклона (горизонтальное изменение).
Загар угла также можно определить как:
\ tan (θ) = \ frac {\ sin (θ)} {\ cos (θ)}
Что такое Arctan?
Тангенс угла технически говорит вам, что возвращает функция tan, когда вы применяете ее к конкретному углу, который вы имеете в виду. Функция под названием «arctan» или tan −1 меняет на обратное значение функции tan и возвращает исходный угол, когда вы применяете его к tan угла. Arcsin и arccos делают то же самое с функциями sin и cos соответственно.
Arcsin и arccos делают то же самое с функциями sin и cos соответственно.
Преобразование касательных в градусы
Преобразование касательных в градусы требует, чтобы вы применили функцию arctan к тангенту угла, который вас интересует. Следующее выражение показывает, как преобразовать касательные в градусы:
\ text {Угол в градусах } = \ arctan (\ tan (θ))
Проще говоря, функция arctan обращает эффект функции tan. Итак, если вы знаете, что tan ( θ ) = √3, тогда:
\ begin {align} \ text {Угол в градусах} & = \ arctan (\ sqrt {3}) \\ & = 60 ° \ end {align}
На калькуляторе нажмите кнопку «tan -1 », чтобы применить функцию арктангенса.Вы делаете это либо до того, как вводите значение, для которого хотите взять арктангенс, либо после, в зависимости от вашей конкретной модели калькулятора.
Пример задачи: направление движения лодки
Следующая задача иллюстрирует полезность функции загара. Представьте, что кто-то движется на лодке со скоростью 5 метров в секунду в восточном направлении (с запада), но движется по течению, толкающему лодку на север со скоростью 2 метра в секунду. Под каким углом получается направление движения на восток?
Представьте, что кто-то движется на лодке со скоростью 5 метров в секунду в восточном направлении (с запада), но движется по течению, толкающему лодку на север со скоростью 2 метра в секунду. Под каким углом получается направление движения на восток?
Разбейте проблему на две части.Во-первых, движение на восток можно рассматривать как формирование прилегающей стороны треугольника (длиной 5 метров в секунду), а течение, движущееся на север, можно рассматривать как противоположную сторону этого треугольника (с длина 2 метра в секунду). Это имеет смысл, потому что окончательное направление движения (которое будет гипотенузой на гипотетическом треугольнике) является результатом комбинации эффекта движения на восток и течения, толкающего на север. Физические задачи часто включают создание подобных треугольников, поэтому для решения можно использовать простые тригонометрические отношения.
\ tan (θ) = \ frac {\ text {противоположный}} {\ text {смежный}}
Это означает, что загар угла конечного направления движения равен:
\ begin {align} \ tan (θ) & = \ frac {2 \ text {m / s}} {5 \ text {m / s}} \\ & = 0. 4 \ end {align}
4 \ end {align}
Преобразуйте это в градусы, используя тот же подход, что и в предыдущий раздел:
\ begin {выровненный} \ text {Угол в градусах} & = \ arctan (\ tan (θ)) \\ & = \ arctan (0,4) \\ & = 21,8 ° \ end {выровненный}
Итак, лодка движется в направлении 21.8 ° от горизонтали. Другими словами, он все еще движется в основном на восток, но он также перемещается немного на север из-за течения.
Функции Arctan Excel: использование ATAN и ATAN2 для вычисления обратного тангенса
В Excel есть две функции для вычисления арктангенса или арктангенса. Эти две функции — ATAN и ATAN2 (atan — сокращение от arctangent), и каждая из них имеет определенное применение в зависимости от желаемых результатов, которые вы хотите получить, и доступных входных данных.В общем, я бы рекомендовал использовать ATAN, если:
- Вас интересует только первый квадрант единичной окружности
- Вы не знаете значений x и y
Однако используйте функцию ATAN2, если:
- Вы хотите вернуть углы во всех четырех квадрантах единичной окружности
- Вы знаете значения x и y
Использование ATAN для вычисления Арктана в Excel
Функция ATAN возвращает результат в диапазоне от -π / 2 до π / 2 радиан (или от -90 до 90 градусов), или, другими словами, в первом и четвертом квадрантах.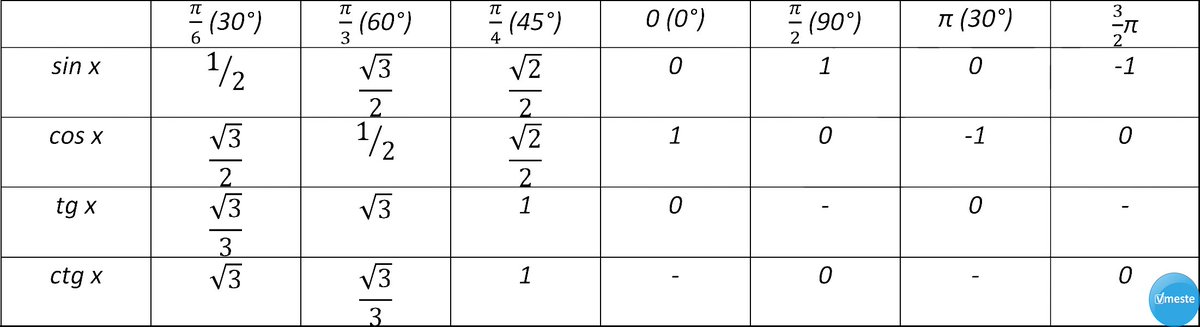
Синтаксис:
ATAN (номер)
У ATAN есть только один аргумент: число, от которого вы хотите вычислить арктангенс. А поскольку аргумент только один, Excel не может определить, в каком квадранте должно находиться решение.
Чтобы продемонстрировать это, я создал единичную окружность в электронной таблице, показанной ниже, создав серию углов от 0 до 360 градусов и вычислив значения x и y с помощью функций COS и SIN , соответственно:
Затем я вычислил арктангенс y относительно x с помощью ATAN, и, поскольку Excel работает с углами в радианах, я преобразовал результат в градусы с помощью функции DEGREES.Формула выглядела так:
= ГРАДУСЫ (ATAN (y / x))
Здесь следует отметить несколько вещей:
- Абсолютные значения углов никогда не превышают 90 градусов, а
- Значения во втором (II) квадранте столбца C теперь находятся в четвертом квадранте столбца F.

- Значения в третьем (III) квадранте столбца C теперь находятся в первом квадранте столбца F.
Нанесение результатов на единичную окружность выглядит так:
Как видите, Excel ограничил результаты первым и четвертым квадрантами.Почему это случилось?
Так как у функции ATAN есть только один аргумент, Excel вычисляет значение y / x перед вычислением функции ATAN.
Таким образом, он не может определить, является ли входной сигнал ATAN отрицательным, потому что значение x или значение y отрицательно. Следовательно, он не может сказать, должен ли результат находиться во втором или четвертом квадранте, поэтому по умолчанию используется только четвертый квадрант.
Аналогичным образом, когда входное значение положительное, исходный квадрант может быть либо первым (оба положительных x и y), либо третьим (оба x и y отрицательны).
Мы могли бы использовать сложную вложенную функцию ЕСЛИ, чтобы вернуть результаты во все четыре квадранта, но, к счастью, в Excel есть еще одна функция под названием ATAN2, которая нам поможет.
Использование ATAN2 для вычисления Арктана в Excel
Функцию ATAN2 также можно использовать для вычисления арктангенса в Excel. Эта функция возвращает результат между -π и π радиан (или от -180 до 180 градусов), используя все четыре квадранта. Синтаксис:
ATAN2 (x_num, y_num)
Есть два аргумента:
- Значение x «x_num»
- Значение y «y_num»
Введя в функцию два значения, Excel может определить, к какому квадранту относится это значение.
- Квадрант 1, если оба x и y положительны
- Квадрант 2, если x отрицательный, а y положительный
- Квадрант 3, если оба значения x и y отрицательны
- Квадрант 4, если x положительный, а y отрицательный
Итак, если мы воспользуемся формулой
= ГРАДУСЫ (ATAN2 (x_num, y_num))
Получаем следующие результаты:
Результаты, нанесенные на единичную окружность, выглядят следующим образом:
Итак, очевидно, что эта функция возвращает значения во всех четырех квадрантах. Однако, если мы предпочитаем получать результаты в виде угла от 0 до 360 градусов, а не от -180 до 180, мы можем использовать простую функцию ЕСЛИ, чтобы добавить 360, если результат меньше 0.
Однако, если мы предпочитаем получать результаты в виде угла от 0 до 360 градусов, а не от -180 до 180, мы можем использовать простую функцию ЕСЛИ, чтобы добавить 360, если результат меньше 0.
= ЕСЛИ (результат <0, результат + 360, результат)
Заключение
Надеюсь, теперь вы понимаете ограничения ATAN и понимаете, когда лучше использовать ATAN2 для вычисления арктангенса или арктангенса в Excel.
Как правило, используйте ATAN, если:
- Вы работаете только в первом квадранте
- Вы не знаете значений x или y
Используйте функцию ATAN2, если:
- Углы нужны во всех четырех квадрантах
- Значения x и y известны
Диаграмма касательного синуса и косинуса.Каждый градус со специальными углами
В этой таблице приведены десятичные значения для каждого угла от 0 ° до 90 °.
| Уголок | синус | Косинус | Касательная |
| 0 ° | 0 | 1 | 0 |
| 1 ° | 0.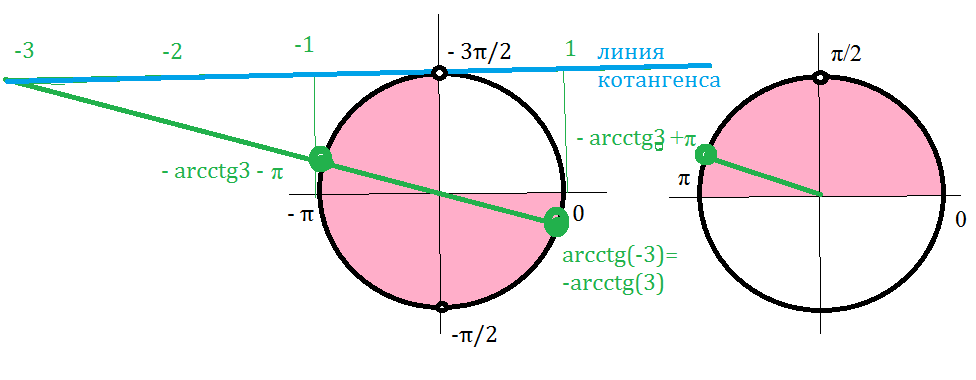 01745 01745 | 0,99985 | 0,01746 |
| 2 ° | 0,03490 | 0,99939 | 0,03492 |
| 3 ° | 0,05234 | 0,99863 | 0,05241 |
| 4 ° | 0.06976 | 0,99756 | 0,06993 |
| 5 ° | 0,08716 | 0,99619 | 0,08749 |
| 6 ° | 0,10453 | 0,99452 | 0,10510 |
| 7 ° | 0. 12187 12187 | 0,99255 | 0,12278 |
| 8 ° | 0,13917 | 0,99027 | 0,14054 |
| 9 ° | 0,15643 | 0,98769 | 0,15838 |
| 10 ° | 0.17365 | 0,98481 | 0,17633 |
| 11 ° | 0,19081 | 0,98163 | 0,19438 |
| 12 ° | 0.20791 | 0,97815 | 0,21256 |
| 13 ° | 0.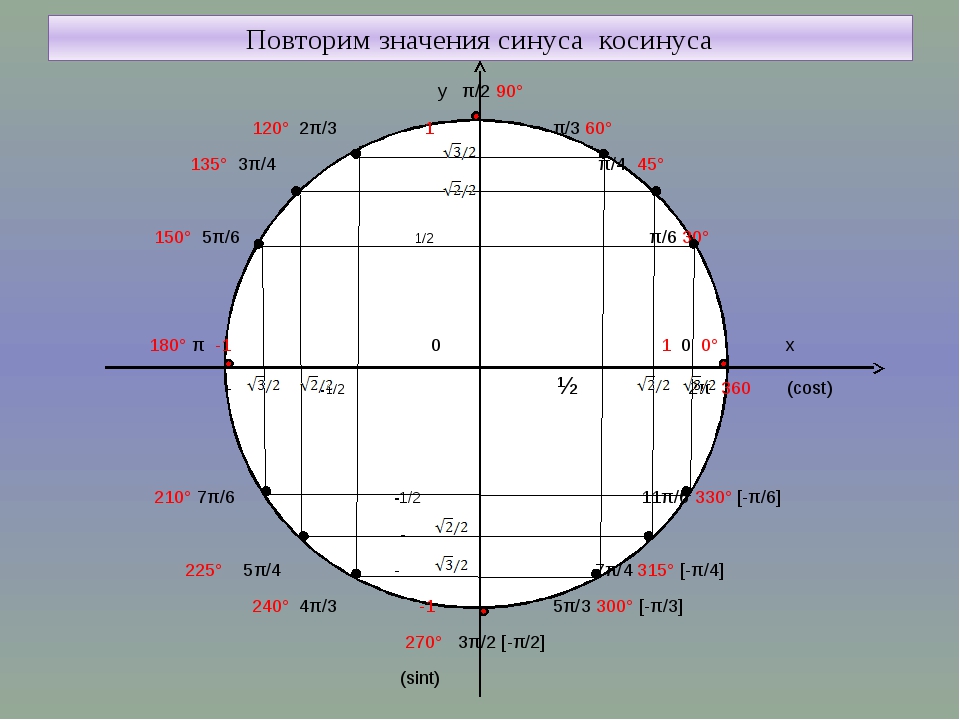 22495 22495 | 0,97437 | 0,23087 |
| 14 ° | 0,24192 | 0,97030 | 0,24933 |
| 15 ° | 0,25882 | 0,96593 | 0,26795 |
| Уголок | синус | Косинус | Касательная |
| 31 ° | 0.51504 | 0,85717 | 0,60086 |
| 32 ° | 0,52992 | 0,84805 | 0,62487 |
| 33 ° | 0,54464 | 0,83867 | 0,64941 |
| 34 ° | 0. 55919 55919 | 0,82904 | 0,67451 |
| 35 ° | 0,57358 | 0,81915 | 0,70021 |
| 36 ° | 0,58779 | 0.80902 | 0,72654 |
| 37 ° | 0.60182 | 0,79864 | 0,75355 |
| 38 ° | 0,61566 | 0,78801 | 0,78129 |
| 39 ° | 0,62932 | 0,77715 | 0.80978 |
| 40 ° | 0. 64279 64279 | 0,76604 | 0,83910 |
| 41 ° | 0,65606 | 0,75471 | 0,86929 |
| 42 ° | 0,66913 | 0,74314 | 0, |
| 43 ° | 0.68200 | 0,73135 | 0,93252 |
| 44 ° | 0,69466 | 0,71934 | 0,96569 |
| 45 ° | 0,70711 или | 0.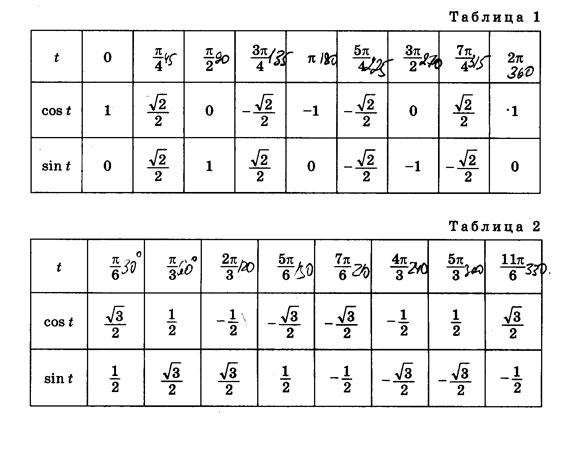 70711 или 70711 или | 1 |
| Уголок | синус | Косинус | Касательная | |
| 61 ° | 0.87462 | 0,48481 | 1.80405 | |
| 62 ° | 0,88295 | 0,46947 | 1,88073 | |
| 63 ° | 0,89101 | 0,45399 | 1.96261 | |
| 64 ° | 0. 89879 89879 | 0,43837 | 2.05030 | |
| 65 ° | 0, | 0,42262 | 2.14451 | |
| 66 ° | 0, | 0,40674 | 2.24604 | |
| 67 ° | 0. | 0,39073 | 2.35585 | |
| 68 ° | 0, | 0,37461 | 2.47509 | |
| 69 ° | 0,93358 | 0,35837 | 2,60509 | |
| 70 ° | 0. 93969 93969 | 0,34202 | 2,74748 | |
| 71 ° | 0,94552 | 0,32557 | 2. | |
| 72 ° | 0,95106 | 0,30902 | 3,07768 | |
| 73 ° | 0.95630 | 0,29237 | 3,27085 | |
| 74 ° | 0,96126 | 0,27564 | 3,48741 | |
| 75 ° | 0,96593 | 0,25882 | 3,73205 |
| Угол | синус | Косинус | Касательная |
| 76 ° | 0. 97030 97030 | 0,24192 | 4.01078 |
| 77 ° | 0,97437 | 0,22495 | 4.33148 |
| 78 ° | 0,97815 | 0.20791 | 4,70463 |
| 79 ° | 0.98163 | 0,19081 | 5.14455 |
| 80 ° | 0,98481 | 0,17365 | 5.67128 |
| 81 ° | 0,98769 | 0,15643 | 6.31375 |
| 82 ° | 0. 99027 99027 | 0,13917 | 7.11537 |
| 83 ° | 0,99255 | 0,12187 | 8.14435 |
| 84 ° | 0,99452 | 0,10453 | 9,51436 |
| 85 ° | 0.99619 | 0,08716 | 11.43005 |
| 86 ° | 0,99756 | 0,06976 | 14.30067 |
| 87 ° | 0,99863 | 0,05234 | 19.08114 |
| 88 ° | 0. 99939 99939 | 0,03490 | 28,63625 |
| 89 ° | 0,99985 | 0,01745 | 57.28996 |
| 90 ° | 1 | 0 | Не определено |
Функция ATAN — служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции ATAN в Microsoft Excel.
Описание
Возвращает арктангенс или арктангенс числа. Арктангенс — это угол, тангенс которого равен числу . Возвращаемый угол указывается в радианах в диапазоне от -pi / 2 до pi / 2.
Возвращаемый угол указывается в радианах в диапазоне от -pi / 2 до pi / 2.
Синтаксис
ATAN (номер)
Аргументы функции ATAN следующие:
Замечание
Чтобы выразить арктангенс в градусах, умножьте результат на 180 / PI () или используйте функцию ГРАДУСЫ.
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter. При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные.
При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные.
Формула | Описание | Результат |
|---|---|---|
= ATAN (1) | Арктангенс единицы в радианах, пи / 4 | 0.785398163 |
= ATAN (1) * 180 / PI () | Арктангенс единицы в градусах | 45 |
= ГРАДУСЫ (ATAN (1)) | Арктангенс единицы в градусах | 45 |
Математическая сцена — синус, косинус и тангенс тригонометрии
Математическая сцена — синус, косинус и тангенс тригонометрии — Урок 1 2008 Rasmus ehf | Синус, косинус и тангенс тригонометрии. | Печать |
Урок 1
ABC — прямоугольный треугольник
Угол А составляет 30 градусов. Мы пишем это как: |
a — это обозначение стороны противоположного угла A
b — это обозначение стороны противоположного угла B
c — это обозначение стороны противоположного угла C
Подобные треугольники треугольники, в которых все углы в одном треугольнике равны углам в другой треугольник
Эти два треугольника похожи.Отношение между двумя сторонами в одном треугольнике равно соотношение между соответствующими сторонами в другом треугольнике. |
Использование обозначений в треугольниках выше получаем следующее:
Соотношение зависит
по размеру угла.
Касательная
Отношение, называемое тангенсом (тангенс) острого угла в прямоугольном треугольнике определяется как соотношение между стороной, противоположной углу, и стороной, прилегающей к углу. |
Пример 1 Найти угол A
Первая Тан A = 3 / 4 = 0,75 |
Нам нужно используйте обратную функцию для tan, tan -1 , найти угол. Эта функция находится на той же клавише калькулятора, что и загар. функция (сдвиг загара).
Мы используем следующая последовательность команд:
сдвиг — загар -1 0,75 = 37
Попробуйте следующее на калькуляторе, чтобы увидеть разницу между загаром и загаром -1 :
угол → соотношение соотношение → угол
загар 37 = 0,75 тангенса -1 0,75 = 37
Пример 2 Найти сторона b
коричневый 37 = 4 / b загар 37 b = 4 0. b = 5,3 |
Sne
Синус (грех) острый угол в прямоугольном треугольнике — это соотношение между сторона, противоположная углу и гипотенуза треугольника. |
Пример 3 Найдите угол А, дающий ответ с точностью до градуса.
sin A = 3 / 5 = 0,6 дает <А = 37 Сдвиг грех -1 0,6 = 37 |
Пример 4 Найдите сторону а.
грех 37 = a / 5 а = грех 37 5 а = 3 |
Косинус
Косинус (cos)
острый угол в прямоугольном треугольнике — это соотношение сторон
рядом с углом и гипотенузой треугольника. |
Пример 5 Используйте функцию косинуса, чтобы найти угол A, дающий ответ до ближайшего степень.
cos A = 4 / 5 = 0,8 дает Сдвиг cos -1 0,8 = 37 |
Пример 6 Найдите сторону b.
cos 37 = b / 5 b = Cos 37 5 б = 4 |
некоторые значения для sin, cos и tan.
| грех 80 = 0,98 | cos 80 = 0,17 | загар 80 = 5,67 |
| грех 60 = 0,87 | cos 60 = 0,5 | загар 60 = 1,73 |
| грех 30 = 0,5 | cos 30 = 0,87 | загар 30 = 0,58 |
грех 10
= 0. 17 17 | cos 10 = 0,98 | загар 10 = 0,18 |
Попрактикуйтесь в этих методах, а затем воспользуйтесь тест по тригонометрии 1 (sin, cos и tan).
Триггерная функция | R Документация
Тригонометрические функции
Эти функции дают очевидные тригонометрические функции. Oни соответственно вычислить косинус, синус, тангенс, арккосинус, арксинус, арктангенс и арктангенс с двумя аргументами.
cospi (x) , sinpi (x) и tanpi (x) , вычислить cos (pi * x) , sin (pi * x) и tan (pi * x) .
- Ключевые слова
- математика
Использование
cos (x)
грех (х)
загар (x) acos (x)
asin (х)
атан (х)
atan2 (y, x)
cospi (x)
sinpi (х)
tanpi (x)
Аргументы
- х, у
числовых или комплексных векторов.

Детали
Арктангенс двух аргументов atan2 (y, x) возвращает угол
между осью x и вектором от начала координат до \ ((x, y) \),
т.е. для положительных аргументов atan2 (y, x) == atan (y / x) .
Для стандартных версий углы указаны в радианах, а не в градусах (т.е.
прямой угол равен \ (\ pi / 2 \)), а в «полувращениях» для коспи и т. Д.
cospi (x) , sinpi (x) и tanpi (x) являются точными
для значений x , кратных половине.
Все, кроме atan2 , являются внутренними универсальными примитивами
функции: методы могут быть определены для них индивидуально или через Math группа generic.
Это все оболочки к одноименным системным вызовам (с префиксом c для сложных аргументов), если возможно. ( коспи , sinpi и tanpi являются частью расширения C11
и предоставляется, например, macOS и Solaris: где еще нет
доступный вызов cos и т. д. используются, в особых случаях
для кратных половине.)
д. используются, в особых случаях
для кратных половине.)
Значение
tanpi (0,5) равно NaN . Аналогично для других входов
с дробной частью 0,5 .
Комплексные значения
Для обратных тригонометрических функций сечения ветвей определены, как в Абрамовиц и Стегун, рисунок 4.4, страница 79.
Для asin и acos есть два разреза, оба вдоль
действительная ось: \ (\ left (- \ infty, -1 \ right] \) и
\ (\ left [1, \ infty \ right) \).
Для atan есть два разреза, оба по чисто воображаемому
ось: \ (\ left (- \ infty i, -1i \ right] \) и
\ (\ left [1i, \ infty i \ right) \).
Поведение при резке соответствует стандарту C99, который требует непрерывности обхода конечной точки против часовой стрелки направление.
Комплексные аргументы для cospi , sinpi и tanpi еще не реализованы, и они являются «будущим направлением»
ИСО / МЭК TS 18661-4.
S4 методы
Все, кроме atan2 , являются универсальными функциями S4: методы могут быть определены
для них индивидуально или через Math группа generic.
Список литературы
Беккер Р. А., Чемберс Дж. М. и Уилкс А. Р. (1988) Новый язык S . Уодсворт и Брукс / Коул.
Abramowitz, M. и Stegun, I.A. (1972). Справочник по Математические функции .Нью-Йорк: Дувр. Глава 4. Элементарные трансцендентные функции: логарифмические, Экспоненциальные, круговые и гиперболические функции
Для cospi , sinpi и tanpi расширение C11
ISO / IEC TS 18661-4: 2015 (проект в
http://www.open-std.org/jtc1/sc22/wg14/www/docs/n1950.pdf).
Псевдонимы
- Триг
- cos
- грех
- загар
- acos
- arccos
- asin
- арксин
- атан
- арктан
- атан2
- коспи
- синпи
- танпи
Примеры
библиотека (базовая) # NOT RUN {
x <- seq (-3, 7, by = 1/8)
tx <- cbind (x, cos (pi * x), cospi (x), sin (pi * x), sinpi (x),
тан (пи * х), танпи (х), разорвать.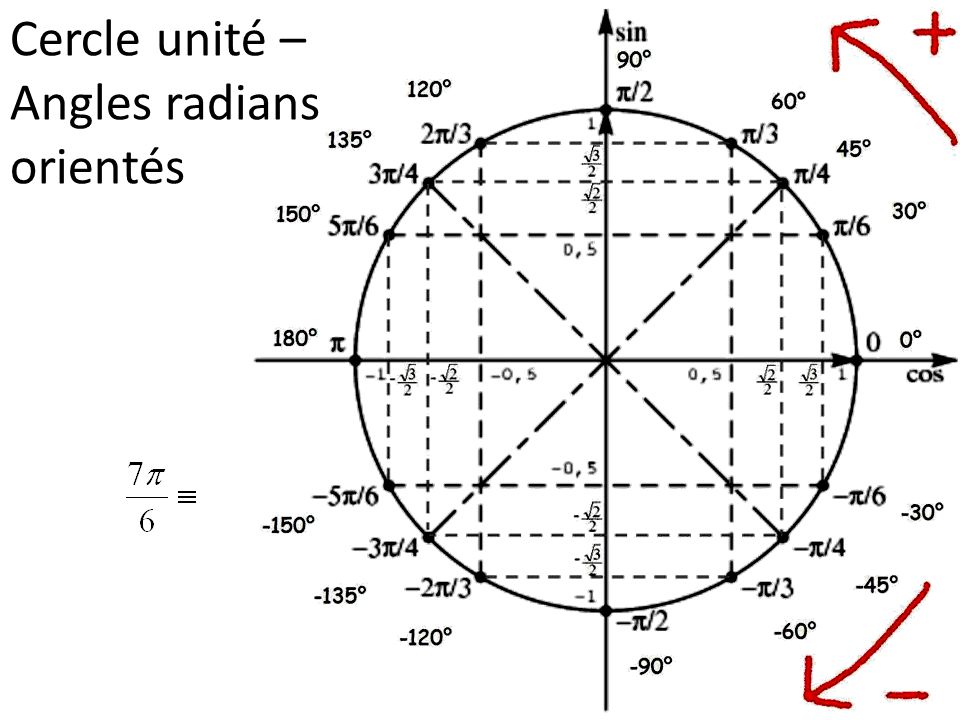

 0174
0174 2308
2308 4663
4663 7535
7535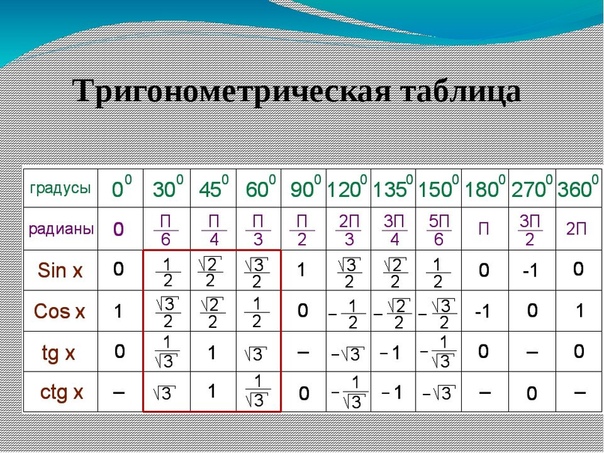 1504
1504 804
804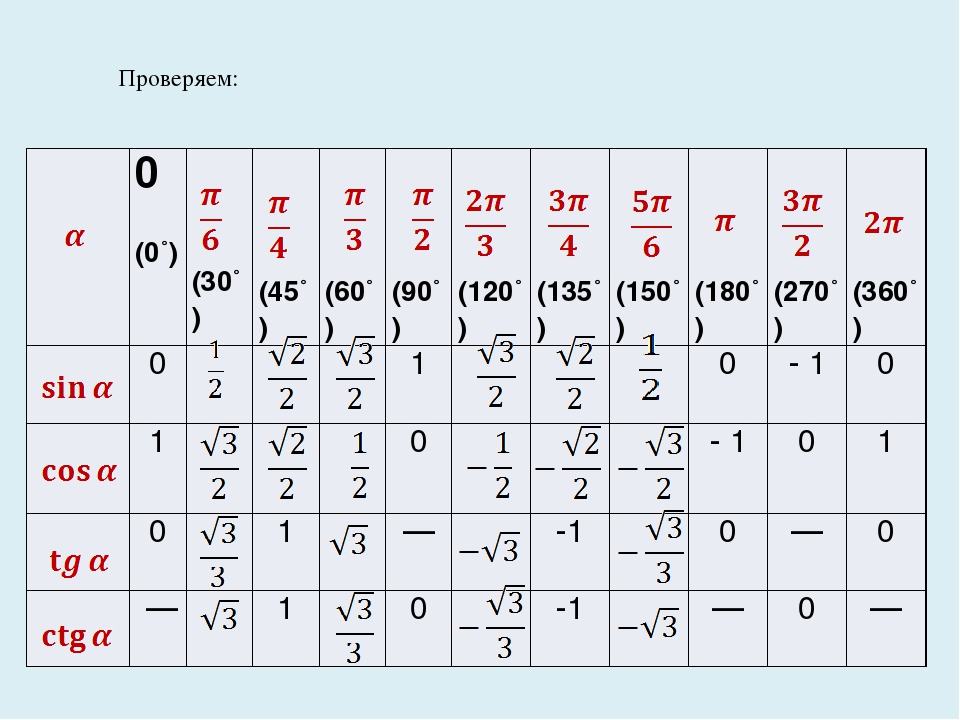 2709
2709 4301
4301 3007
3007 4874
4874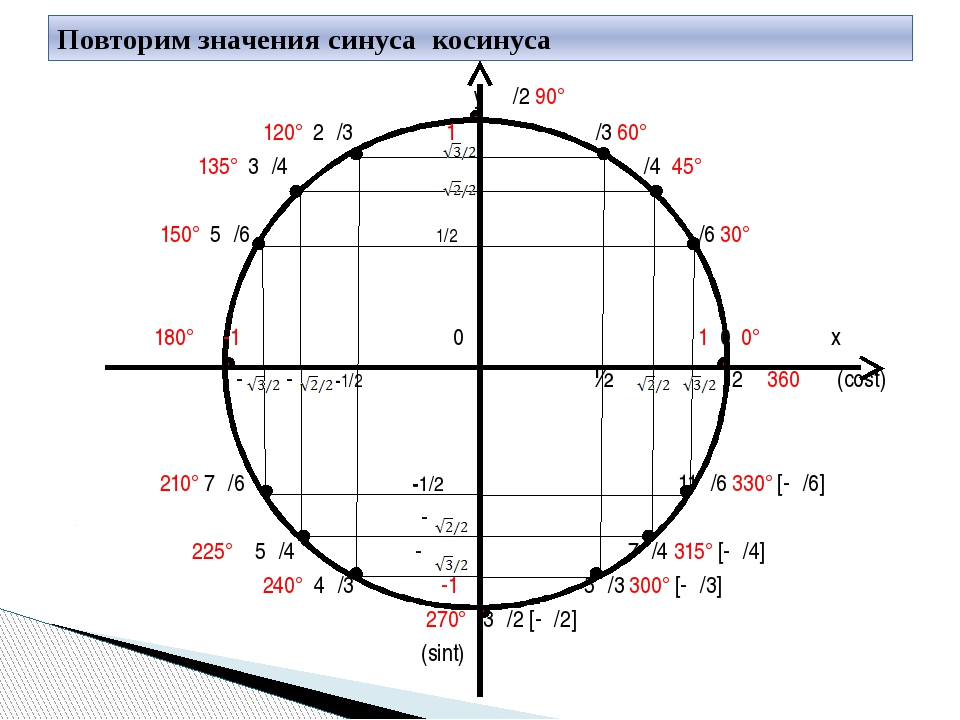 8807
8807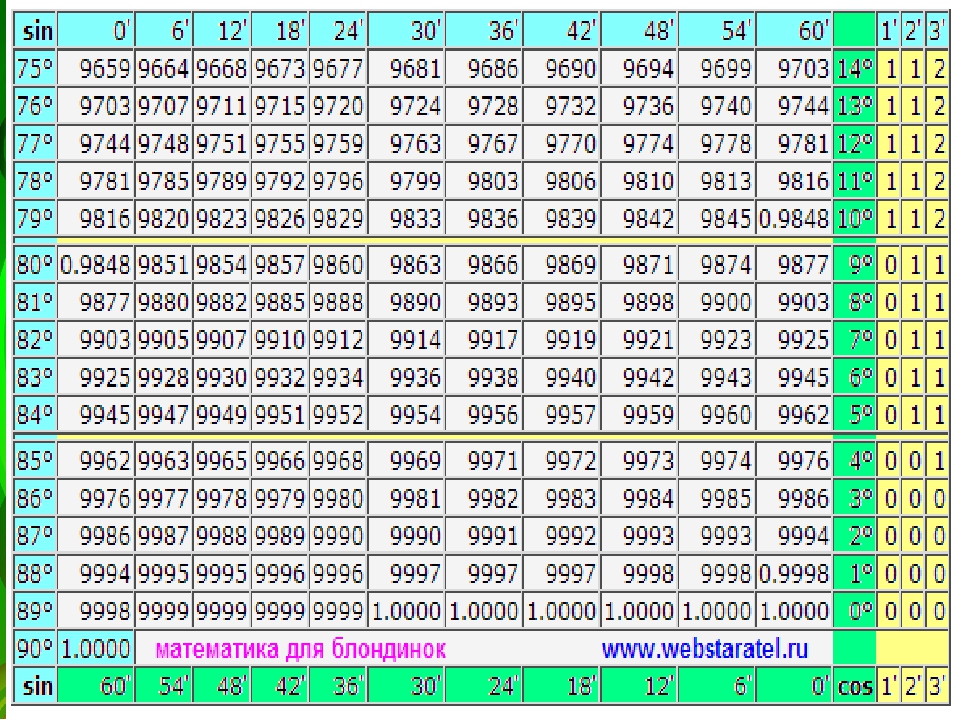 1918
1918 7813
7813 4877
4877 2493
2493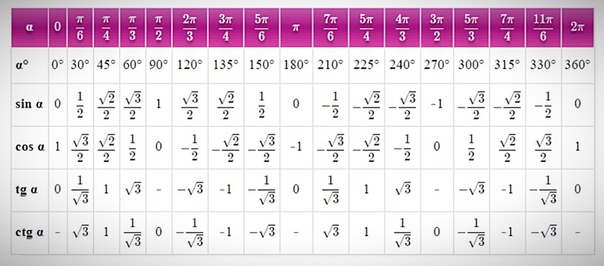 0349
0349 1227
1227 3249
3249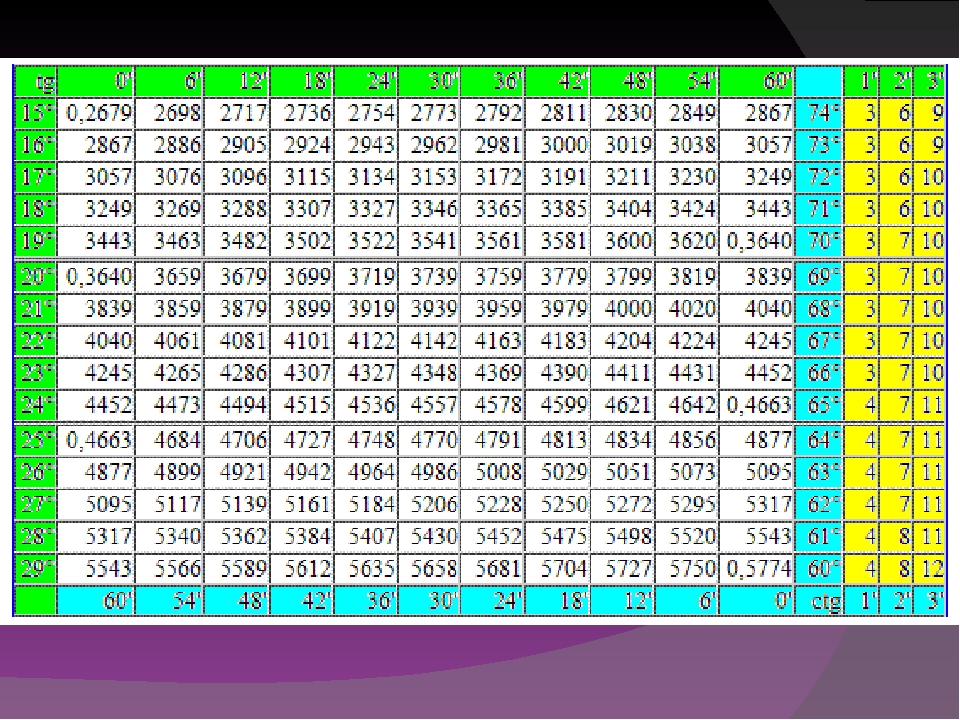 5543
5543 8390
8390 2349
2349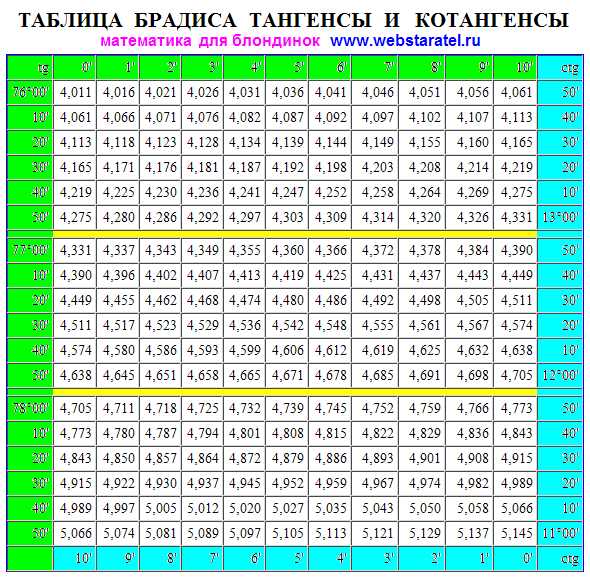 8807
8807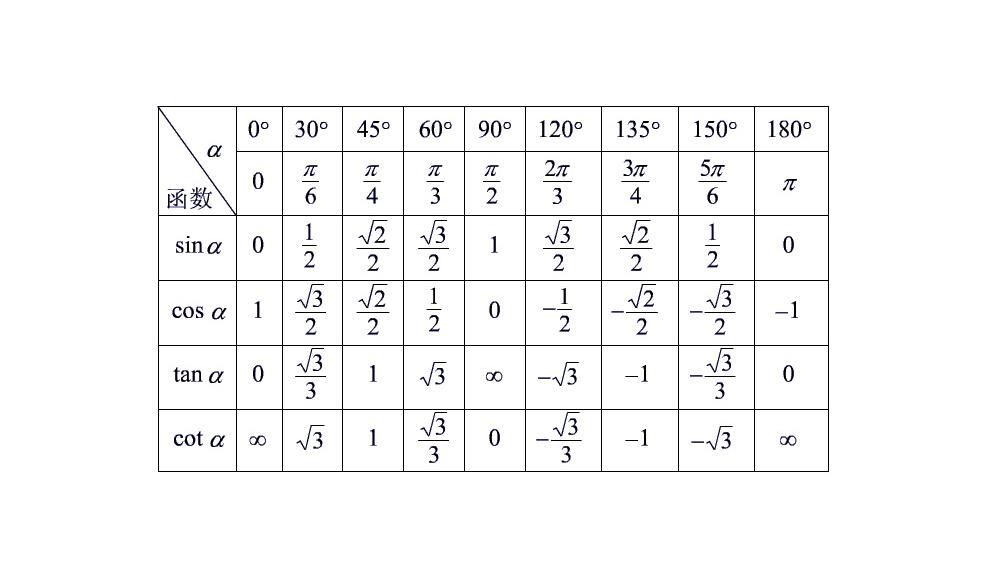 2709
2709 5144
5144 6363
6363 7046
7046 3559
3559 4826
4826 9657
9657 6494
6494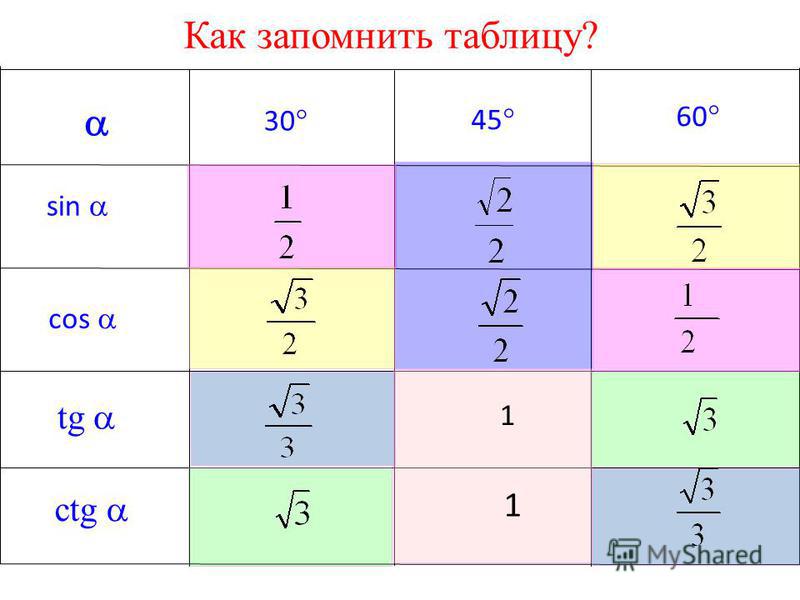 404
404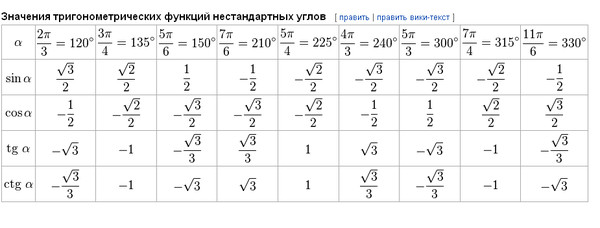 1943
1943 364
364 9657
9657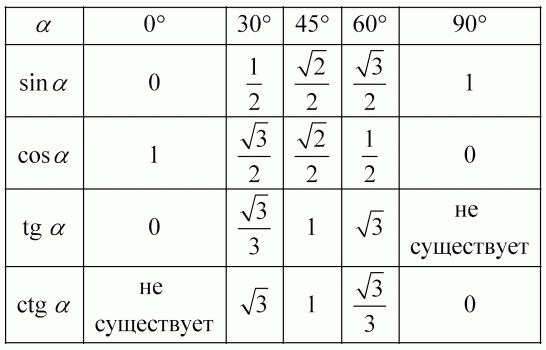 4751
4751 6363
6363 1445
1445 9004
9004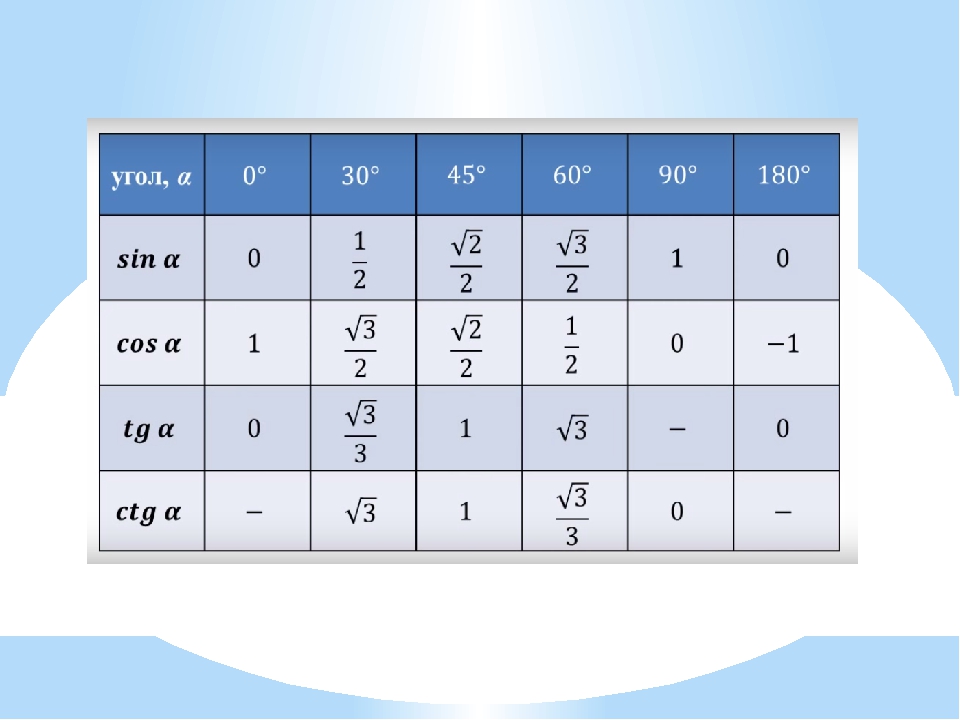 3443
3443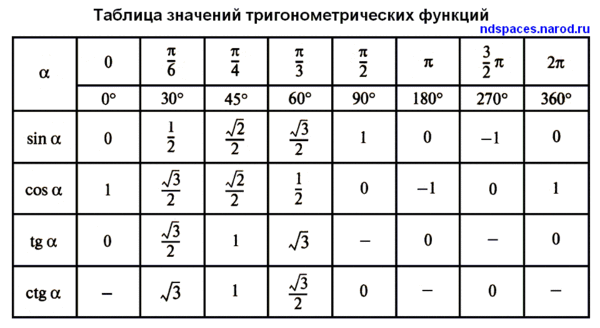 0349
0349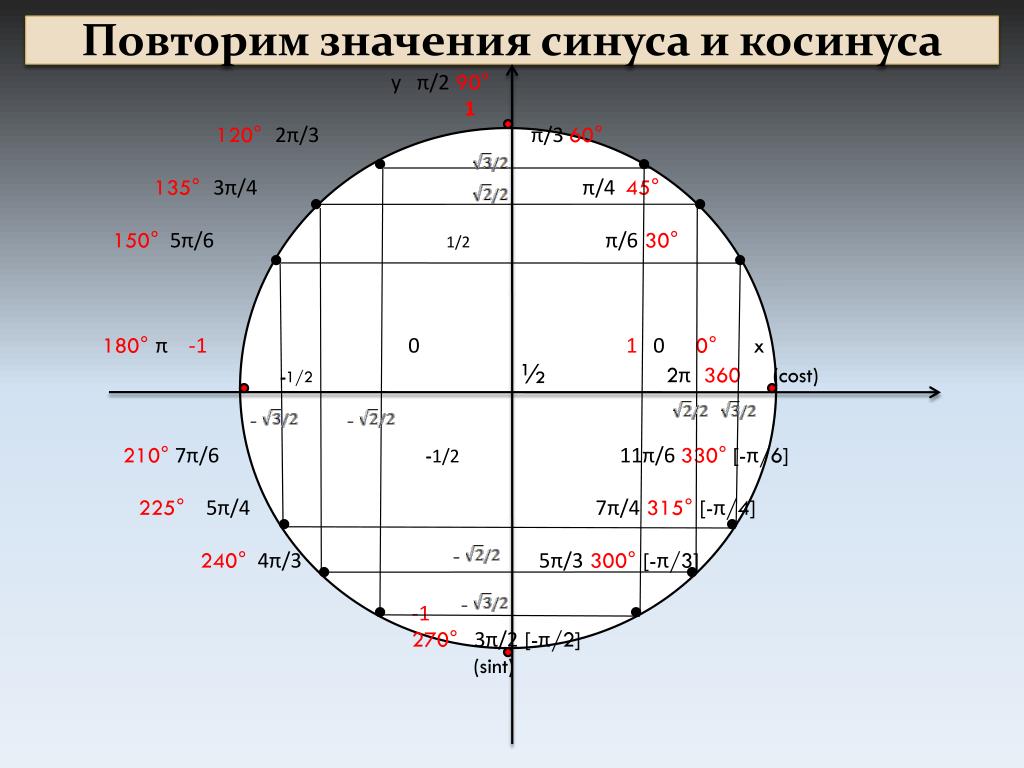 4877
4877 1918
1918 2709
2709 1443
1443 7321
7321 7536
7536 2493
2493
 .. (приблизительно 22/7 = 3,1428)
.. (приблизительно 22/7 = 3,1428)  0175
0175 0698
0698  1222
1222  1745
1745 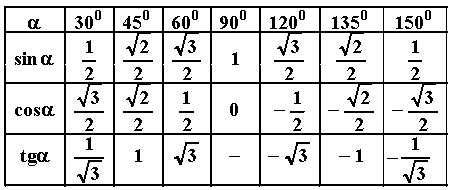 2269
2269  3090
3090  3316
3316  3746
3746 4363
4363  0996
0996  0472
0472  7013
7013 7771
7771 6691
6691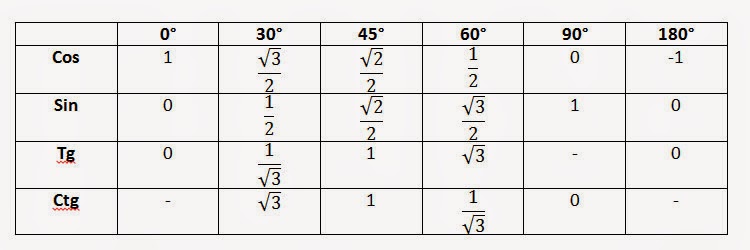 7854
7854 
 75 б = 4
75 б = 4
