Tg квадрат: Тангенс в квадрате, формула и примеры

Тригонометрические тождества и преобразования

Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:

Простейшие тригонометрические тождества

Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств. 
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).

Преобразование отрицательных углов тригонометрических функций (четность и нечетность)

Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.

Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.

Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.

Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)

Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:

Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:

Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла

Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла

Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица

Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла

Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.

Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла

Формулы универсальной тригонометрической подстановки

Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем  α/2 .

Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.

Тригонометрические тождества преобразования половины угла

Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.
Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.

Тригонометрические формулы сложения углов

cos (α — β) = cos α · cos β + sin α · sin β

sin (α + β) = sin α · cos β + sin β · cos α 

sin (α — β) = sin α · cos β — sin β · cos α 
cos (α + β) = cos α · cos β — sin α · sin β 

Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:

Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.

Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.

Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.

Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.

Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.

Формулы преобразования суммы или разности тригонометрических функций

Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:

Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα

Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.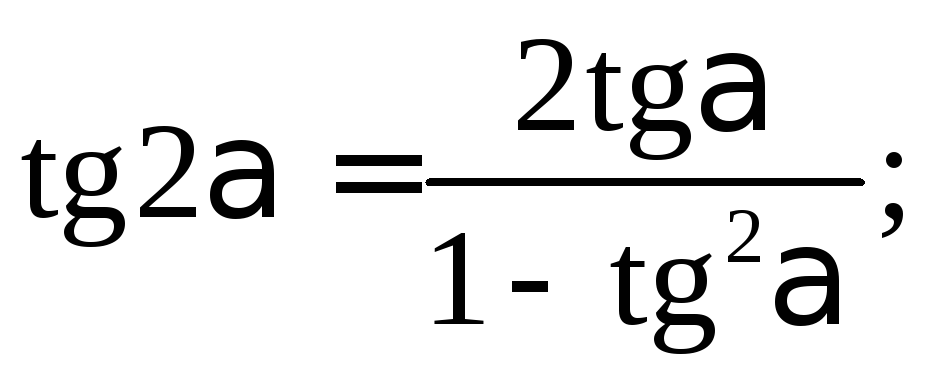
В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:

Формулы преобразования произведения тригонометрических функций

Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:

В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.

Формулы приведения тригонометрических функций

Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90)  = cos α .

См. также Полный список формул приведения тригонометрических функций.

Угол	α + 90 α + π/2	α + 180 α + π	α + 270 α + 3π/2	90 — α π/2- α	180 — α π- α	270 — α 3π/2- α	360 — α 2π- α
sin	cos α	-sin α	-cos α	cos α	sin α	-cos α	-sin α
cos	-sin α	-cos α	sin α	sin α	-cos α	-sin α	cos α
tg	-ctg α	tg α	-ctg α	ctg α	-tg α	ctg α	-tg α
ctg	-tg α	ctg α	-tg α	tg α	-ctg α	tg α	-ctg α

 Начать курс обучения

1 tg в квадрате

Вы искали 1 tg в квадрате? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 tg это, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 tg в квадрате».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 1 tg в квадрате,1 tg это,1 tgx,1 косинус 2 альфа,2 cos чему равен,2 косинус,2 синус в квадрате х,2 синус в квадрате х синус х,2 синус косинус,cos 2 y,cos 2 чему равен,cos 2x в квадрате,cos sin чему равно,cos x 2,cos x sin y,cos x в квадрате,cos x квадрат,cos y,cos y 2,cos y sin y,cos в квадрате,cos в квадрате 2x,cos делить на sin,cos квадрат x cos x,cos на sin,cos на sin делить,cos умножить sin,cos умножить на sin,cos х п,cos через sin,cos2x,cosx sinx это,cosx tgx sinx,l sin,sin 2 t,sin cos умножить,sin sinx,sin t 2,sin x cos x tg x,sin x cos y sin y cos x,sin x sin y,sin x sinx,sin x в квадрате,sin в квадрате x,sin делить на cos,sin квадрат x,sin на cos делить,sin на cos умножить,sin умножить cos,sin умножить на cos,sin через cos,sin2t,sinx cosx tgx,sinx siny,sinx siny формула,tg x 2,tg x в квадрате,tg3x,tgx cosx,tgx ctgx равно,y sin x cos 2 x,косинус 2 икс,косинус 2 х синус х,косинус двух икс,косинус п 2 х,син х син у,синус 2 икс,синус 2 х в квадрате,синус 2х,синус в квадрате 2 х,синус в квадрате х 2,синус двух икс,синус х,синус х 2,синус х у,формула cosx cosy,формулы sinx a,чему равен cos 2,чему равно cosx sinx.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 1 tg в квадрате. Просто введите задачу в окошко и нажмите «решить» здесь (например, 1 tgx).

Где можно решить любую задачу по математике, а так же 1 tg в квадрате Онлайн?

Решить задачу 1 tg в квадрате вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Основное Тригонометрическое Тождество — Доказательство

Связь между sin и cos одного угла

Вы уже наверняка знаете, что тождественный — это равный.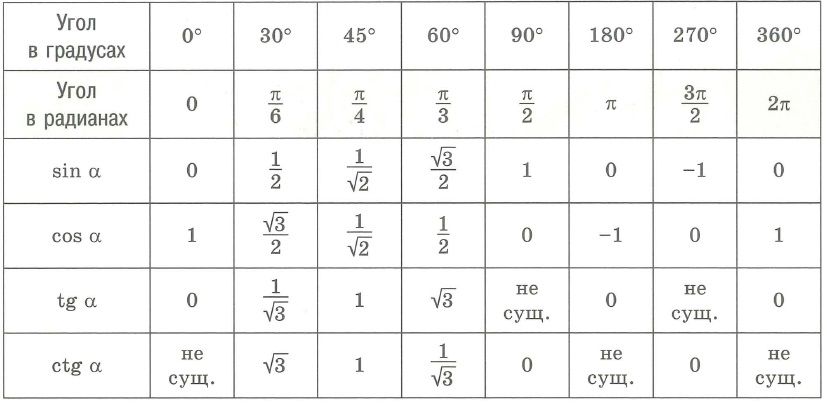  

Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция. 

Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:

Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.

Равенство tg²α + 1 = 1/cos²α и равенство 1 + сtg²α + 1 = 1/sin²α выводят из основного тождества, разделив обе части на sin²α и cos²α.

В результате деления получаем:

Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая. 

sin²α + cos²α = 1

Сумма квадратов синуса и косинуса одного угла тождественно равна единице.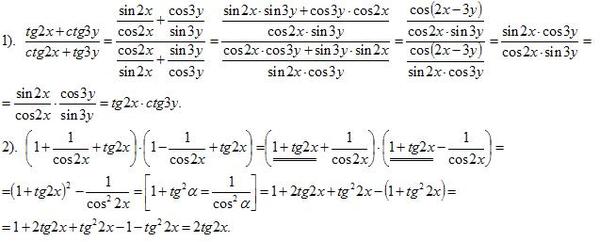

Чтобы доказать тождество, обратимся к теме единичной окружности. 

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.

Докажем тождество sin²α + cos²α = 1

1. Итак, нам известны координаты точки A (1; 0).

   Произвольный угол α, тогда cos α = x0 = ОB.



2. Если развернуть точку A на угол α, то точка A становится на место точки A₁.


3. По определениям:
   • Синус угла (sin α) — это отношение противолежащего катета к гипотенузе. 
   • Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
   Это значит, что точка A₁ получает координаты cos α, sin α.


4. Опускаем перпендикулярную прямую A₁B на x0 из точки A₁.

   Образовался прямоугольный треугольник OA₁B.

   |A₁B| = |у|

   |OB| = |x|.



5. Гипотенуза OA₁ имеет значение, равное радиусу единичной окружности.

   |OA₁| = 1.



6. Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:

   |A₁B|² + |OB|² = |OA₁|².



7. Записываем в виде: |y|² + |x|² = 1².

   Это значит, что y² + x² = 1.
   sin угла α = y
   cos угла α = x



8. Вставляем данные угла вместо координат точек:

   OB = cos α
   A₁B = sin α
   A₁O = 1



9. Получаем основное тригонометрическое тождество: sin²α + cos²α = 1.
   Что и требовалось доказать. 

Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:

• sin α = ±
• cos α = ±

Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.

Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.

 

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Тангенс и котангенс через синус и косинус

Немного вводных:

• Синус угла  — это ордината y.
• Косинус угла  — это абсцисса x.
• Тангенс угла  — это отношение ординаты к абсциссе.  
• Котангенс угла — это отношение абсциссы к ординате.

Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.

• tg α =
• ctg α =

Исходя из определений:

Это позволяет сделать вывод, что тригонометрические тождества 

задаются sin и cos углов.

Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.

Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон. 

• Например,  выражение применимо для любого угла α, не равного + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.

Выражение

применимо для любого угла α, не равного π * z, где z — это любое целое число.  

Связь между тангенсом и котангенсом

Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
 

• Тождество записывается в следующем виде:
  tg α * ctg α = 1.

Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.

Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.

tg α * ctg α = 1.

 

1. По определению:

   tg α = y/x

   ctg α = x/y



2. Отсюда следует, что tg α * ctg α = y/x * x/y = 1


3. Преобразовываем выражение, подставляем  и ,
   получаем:

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.

Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.

Какие, какие числа?🤯

Взаимно обратные числа — это два числа, произведение которых равно 1.

 

Если в голове вашего ребенка бурлит тригонометрическая каша, и все формулы смешались в один нераспутываемый клубок — записывайтесь на бесплатный вводный урок математики в онлайн-школу Skysmart.

Наши преподаватели помогут навести в голове порядок и разложить все знания по полочкам. На уроках вас ждут интересные задачки и располагающая атмосфера, в которой совсем не страшно задавать вопросы и получать от занятий — максимум.

 

Тангенс и косинус, котангенс и синус

Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла  — с синусом.

Эта связь становится очевидна, если взглянуть на тождества:
 

• tg²α + 1 =

Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.

• 1 + ctg²α =

Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.

Вывести оба этих тождества можно из основного тригонометрического тождества:
sin²α + cos²α = 1.
 

 

1. Для этого нужно поделить обе части тождества на cos²α, где косинус не равен нулю.


2. В результате деления получаем формулу tg²α + 1 =


3. Если обе части основного тригонометрического  тождества sin²α + cos²α = 1 разделить на  sin²α, где синус не равен нулю, то получим тождество:
   1 + ctg²α = . 


4. Отсюда можно сделать вывод, что тригонометрическое тождество tg²α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.


5. А тригонометрическое тождество 1 + ctg²α = применимо для любого угла, не равного π * z, где z — это любое целое число.  

Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами. 

Основные тригонометрические тождества

1	sin2α + cos2α = 1
2
3
4	tgα * ctgα = 1
5	tg2α + 1 =
6	1 + ctg2α =

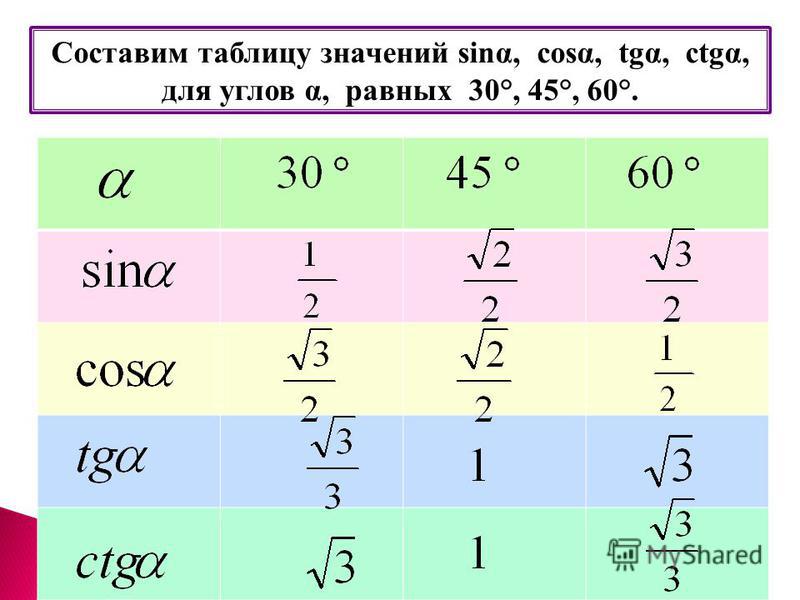
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.

Примеры решения задач

Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.

Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.

Как решаем:

 

1. Чтобы решить задачу, необходимы следующие тригонометрические тождества:



2. Выражаем cos α из тригонометрической единицы:



3. Далее подставляем значения sin α:



4. Вычисляем:



5. Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:



6. Таким же образом, используя формулу, вычисляем значение котангенса:

Ответ:

Задачка 2. Найдите значение cos α,
если:

Как решаем: 

 

1. Чтобы решить задачу, необходимы следующие тригонометрические тождества:



2. Выражаем cos α из тригонометрической единицы:



3. Далее подставляем значения sin α:



4. Вычисляем:
   


5. То же самое проделываем со вторым значение sin α

   Подставляем значения sin α:



6. Вычисляем:

Ответ:

Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств. 4x= \frac{3+4cos2x+cos4x}{8}$$

Формулы сложения аргументов

$$sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta$$

---

$$cos(\alpha + \beta) = cos \alpha cos \beta — sin \alpha sin \beta$$

---

$$tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 — tg \alpha tg \beta}$$

---

$$ctg(\alpha + \beta)= \frac{ctg \alpha ctg \beta -1}{ctg \alpha + ctg \beta}$$

---

$$sin(\alpha — \beta) = sin \alpha cos \beta — cos \alpha sin \beta$$

---

$$cos(\alpha — \beta) = cos \alpha cos \beta + sin \alpha sin \beta$$

---

$$tg(\alpha — \beta)= \frac{tg \alpha — tg \beta}{1 + tg \alpha tg \beta}$$

---

$$ctg(\alpha — \beta)= \frac{ctg \alpha ctg \beta +1}{ctg \alpha — ctg \beta}$$

Формулы суммы тригонометрических функций

$$sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$

---

$$cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$

---

$$tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$

---

$$ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$

---

$$(sin\alpha + cos\alpha)^2= 1+sin2\alpha$$

Формулы разности тригонометрических функций

$$sin\alpha — sin\beta = 2sin \frac{\alpha — \beta }{2} \cdot cos \frac{\alpha + \beta }{2}$$

---

$$cos\alpha — cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha — \beta }{2}$$

---

$$tg\alpha — tg\beta = \frac{sin(\alpha — \beta) }{cos \alpha cos \beta}$$

---

$$ctg\alpha — ctg\beta = — \frac{sin(\alpha — \beta) }{sin \alpha sin \beta}$$

---

$$(sin\alpha + cos\alpha)^2= 1-sin2\alpha$$

Формулы произведения тригонометрических функций

$$sin\alpha \cdot sin\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}$$

---

$$sin\alpha \cdot cos\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}$$

---

$$cos\alpha \cdot cos\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}$$

---

\begin{align} tg\alpha \cdot tg\beta & = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)}\\ &= \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta} \end{align}

---

\begin{align} ctg\alpha \cdot ctg\beta & = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)}\\ &= \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta} \end{align}

---

$$tg\alpha \cdot ctg\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}$$

Формулы приведения тригонометрических функций

Формулы приведения тригонометрических функций

      Формулы привидения тригонометрических функций представлены в виде таблицы.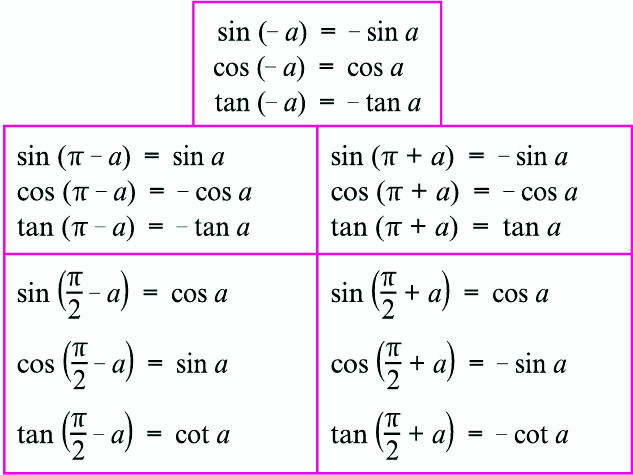 Ниже находятся некоторые формулы приведения в табличном виде. Еще ниже эти формулы приведения расписаны для некоторых тригонометрических функций в виде тригонометрических тождеств.Таблицы значений тригонометрических функций находятся на другой странице.

      Формулы привидения для синуса выглядят так:

sin (π/2 + α) = cos α

sin (π + α) = — sin α

sin (3π/2 + α) = — cos α

sin (π/2 — α) = cos α

sin (π — α) = sin α

sin (3π/2 — α) = — cos α

sin (2π — α) = — sin α

      Формулы приведения для тригонометрической функции синус будут следующие. Синус угла пи пополам (пи/2) плюс или минус угол альфа равняется косинусу угла альфа. Синус угла пи плюс угол альфа или угла два пи минус альфа по формуле приведения будет равен минус синусу угла альфа. Синус угла три вторых пи (3пи/2) плюс или минус альфа равен минус косинусу альфа. Если угол равняется пи минус альфа, то синус такого угла равняется синусу угла альфа. Тригонометрия формулы и тригонометрические тождества. Перевод синуса в косинус.

      Тригонометрические формулы привидения для косинуса приобретают такой вид:

cos (π/2 + α) = — sin α

cos (π + α) = — cos α

cos (3π/2 + α) = sin α

cos (π/2 — α) = sin α

cos (π — α) = — cos α

cos (3π/2 — α) = — sin α

cos (2π — α) = cos α

      Для косинуса формулы приведения имеют следующий вид. Косинус угла пи пополам (пи/2) плюс угол альфа и косинус три вторых пи минус альфа равняются минус синусу угла альфа. Косинус угла пи плюс или минус угол альфа в результате равен минус косинусу альфа. Формула приведения для косинуса угла (3пи/2) три вторых пи плюс угол альфа и пи пополам минус альфа равняется синусу угла альфа. Тригонометрическая функция косинус пи пополам (1/2 пи) минус альфа равняется тригонометрической функции косинус угла альфа. Тригонометрия формулы. Перевод косинуса в синусы.

      Тригонометрическая функция тангенс имеет следующие формулы привидения:

tg (π/2 + α) = — ctg α

tg (π + α) = tg α

tg (3π/2 + α) = — ctg α

tg (π/2 — α) = ctg α

tg (π — α) = — tg α

tg (3π/2 — α) = ctg α

tg (2π — α) = tg α

      Тригонометрические формулы приведения функции тангенс tg. Тангенс угла пи деленное на два плюс альфа и угла три вторых пи плюс альфа приравниваются минус котангенсу угла альфа. Тригонометрическая функция тангенс угла пи на два или три пи деленное на два (3/2 пи) минус альфа равна котангенсу альфа. Тангенс угла пи минус альфа равен минус тангенсу угла альфа. Формулы приведения для тангенса пи плюс альфа и тангенса два пи минус альфа равняются тангенсу угла альфа. Тригонометрические тождества. Перевод тангенса в котангенсы.

      Тригонометрическая функция тангенс имеет следующие формулы привидения:

ctg (π/2 + α) = — tg α

ctg (π + α) = ctg α

ctg (3π/2 + α) = — tg α

ctg (π/2 — α) = tg α

ctg (π — α) = — ctg α

ctg (3π/2 — α) = tg α

ctg (2π — α) = ctg α

      Формулы приведения функции котангенс ctg угла. Для угла 1/2 пи плюс альфа и угла 3/2 пи плюс альфа котангенс равняется минус тангенсу -tg угла альфа. Если в этих же выражениях угол альфа не прибавляется, а вычитается, тогда котангенс такого угла равняется тангенсу угла альфа. Функция котангенс пи минус альфа равна минус котангенсу угла альфа. Котангенс угла пи плюс альфа и 2 пи минус альфа будет равен котангенсу угла альфа. Тригонометрические тождества и формулы тригонометрия.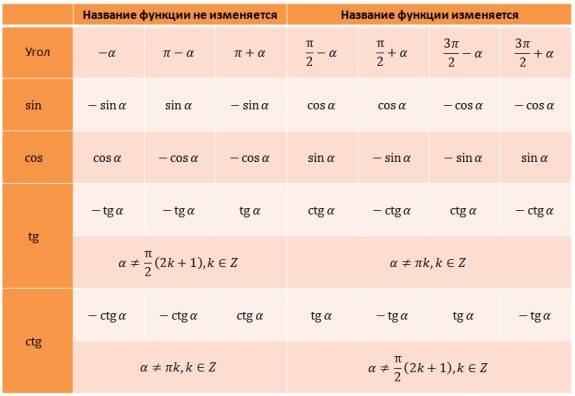 Перевод котангенсов в тангенсы.

Если вам понравилась публикация и вы хотите знать больше, помогите мне в работе над другими материалами.

      17 января 2010 года — 1 декабря 2018 года..

© 2006 — 2021 Николай Хижняк. Все права защищены.

Все формулы по тригонометрии

Все формулы по тригонометрии

Основные тригонометрические тождества

sin²x + cos²x = 1

tgx ctgx = 1

tg2x + 1	=	1
		cos2x

ctg2x + 1	=	1
		sin2x

Формулы двойного аргумента

sin2x = 2sinx cosx

sin2x	=	2tgx	=	2ctgx	=	2
		1 + tg2x		1 + ctg2x		tgx + ctgx

cos2x = cos² — sin²x = 2cos²x — 1 = 1 — 2sin²x

cos2x	=	1 — tg2x	=	ctg2x — 1	=	ctgx — tgx
		1 + tg2x		ctg2x + 1		ctgx + tgx

tg2x	=	2tgx	=	2ctgx	=	2
		1 — tg2x		ctg2x — 1		ctgx — tgx

ctg2x	=	ctg2x — 1	=	ctgx — tgx
		2ctgx		2

Формулы тройного аргумента

sin3x = 3sinx — 4sin³x cos3x = 4cos³x — 3cosx

tg3x	=	3tgx — tg3x
		1 — 3tg2x

ctg3x	=	ctg3x — 3ctgx
		3ctg2x — 1

Формулы половинного аргумента

sin2	x	=	1 — cosx
	2		2

cos2	x	=	1 + cosx
	2		2

tg2	x	=	1 — cosx
	2		1 + cosx

ctg2	x	=	1 + cosx
	2		1 — cosx

tg	x	=	1 — cosx	=	sinx
	2		sinx		1 + cosx

ctg	x	=	1 + cosx	=	sinx
	2		sinx		1 — cosx

Формулы квадратов тригонометрических функций

sin2x	=	1 — cos2x
		2

cos2x	=	1 + cos2x
		2

tg2x	=	1 — cos2x
		1 + cos2x

ctg2x	=	1 + cos2x
		1 — cos2x

sin2	x	=	1 — cosx
	2		2

cos2	x	=	1 + cosx
	2		2

tg2	x	=	1 — cosx
	2		1 + cosx

ctg2	x	=	1 + cosx
	2		1 — cosx

Формулы кубов тригонометрических функций

sin3x	=	3sinx — sin3x
		4

cos3x	=	3cosx + cos3x
		4

tg3x	=	3sinx — sin3x
		3cosx + cos3x

ctg3x	=	3cosx + cos3x
		3sinx — sin3x

Формулы тригонометрических функций в четвертой степени

sin4x	=	3 — 4cos2x + cos4x
		8

cos4x	=	3 + 4cos2x + cos4x
		8

Формулы сложения аргументов

sin(α + β) = sinα cosβ + cosα sinβ cos(α + β) = cosα cosβ — sinα sinβ

tg(α + β)	=	tgα + tgβ
		1 — tgα tgβ

ctg(α + β)	=	ctgα ctgβ — 1
		ctgα + ctgβ

sin(α — β) = sinα cosβ — cosα sinβ cos(α — β) = cosα cosβ + sinα sinβ

tg(α — β)	=	tgα — tgβ
		1 + tgα tgβ

ctg(α — β)	=	ctgα ctgβ + 1
		ctgα — ctgβ

Формулы суммы тригонометрических функций

sinα + sinβ	=  2sin	α + β	∙ cos	α — β
		2		2

cosα + cosβ	=  2cos	α + β	∙ cos	α — β
		2		2

(sinα + cosα)² = 1 + sin2α

tgα + tgβ	=	sin(α + β)
		cosα cosβ

ctgα + ctgβ	=	sin(α + β)
		sinα sinβ

Формулы разности тригонометрических функций

sinα — sinβ	=  2sin	α — β	∙ cos	α + β
		2		2

cosα — cosβ	=  -2sin	α + β	∙ sin	α — β
		2		2

(sinα — cosα)² = 1 — sin2α

tgα — tgβ	=	sin(α — β)
		cosα cosβ

ctgα — ctgβ	=  –	sin(α — β)
		sinα sinβ

Формулы произведения тригонометрических функций

sinα ∙ sinβ	=	cos(α — β) — cos(α + β)
		2

sinα ∙ cosβ	=	sin(α — β) + sin(α + β)
		2

cosα ∙ cosβ	=	cos(α — β) + cos(α + β)
		2

tgα ∙ tgβ	=	cos(α — β) — cos(α + β)	=	tgα + tgβ
		cos(α — β) + cos(α + β)		ctgα + ctgβ

ctgα ∙ ctgβ	=	cos(α — β) + cos(α + β)	=	ctgα + ctgβ
		cos(α — β) — cos(α + β)		tgα + tgβ

tgα ∙ ctgβ	=	sin(α — β) + sin(α + β)
		sin(α + β) — sin(α — β)

Помогите пожалуйста разобраться.

2 — 8x — 1 = 0
Получились корни: х1 ~ -0.1 и х2 ~ 4,1 в итоге получается ~ — 4,1 , но он не совпадает с предложенными ответами. Подскажите что я делаю не так.

@темы: Тригонометрия Иррациональные уравнения (неравенства)

• ← Предыдущая запись
• Следующая запись →

Этот пост будет безвозвратно удален:

Вы уверены в том, что действительно хотите это сделать?

Да Нет

TG Квадрат Обычный | FONTS.

GE

TG Square Обычный Детали В упаковке (-ах) Не входит ни в одну упаковку Подобные шрифты Нет похожих шрифтов Другие исполнения Других версий нет Дополнительная информация შრიფტი TG Square შექმნილია თამარ გედევანიშვილის მიერ.შრიფტი შეიქმნა და დამუშავდა ვექტორულ პროგრამაში 2008 წელს. 2018 მოხდა მისი რედაქტირება და დასრულებული სახე მიიღო (ttf ფორმატის სახით) პროგრამაში FontLab. შრიფტი არ არის მოცულობითი ტექსტებისთვის გათვლილი. ის განკუთვნილია სათაურებისა და დიდი ზომის ტექსტებისათვის. შრიფტი დაწერილია ქართულ უნიკოდზე. TG Square სახეცვლილ ადაპტაციას BankGothic. Комментарии Эта функция пока недоступна

В настоящее время у нас 892 шрифта и 41 пакет »Шрифты, включая символ Лари » Как писать с грузинским Unicode »Конвертер кодирования ДИЗАЙНТбилиси ფონტების ავტორებს გთავაზობთ ნაშრომის დიზაინერულ ჟურნალში გამოქვეყნებას. ინფომაციისთვის დაუკავშირდით რედაქციას მისამართზე: теплос и протеинос точка ком

TG (квадратные символы — экспериментальные, сплошные линии) и DTG (треугольник …

Библиометрический анализ — это метод, позволяющий количественно оценить академическую продукцию посредством анализа существующих документов. Эта статья была направлена ​​на анализ характеристик публикации по теме утилизации отходов картонной упаковки пиролизом.Исследование проводилось в базе данных Web of Science (WOS) компании Clarivate Analytics. Первоначально был произведен поиск статей, в теме которых было слово «Пиролиз», впоследствии статьи были уточнены, добавив термины «Картонные упаковки» и «Тетра Пак». Для выполнения анализа использовался инструмент «Анализ результатов», предоставленный Web of Science (WOS), позволяющий генерировать информацию, связанную с количеством публикаций, странами, областями исследований и типами публикаций, в дополнение к VOSviewer и CiteSpace. программное обеспечение, позволяющее создавать сети для соавторства организации, соавторства страны, соавторства авторов, совместного цитирования ссылок, совместного цитирования журналов и совпадения ключевых слов и, наконец, матрицы SWOT (сильные и слабые стороны, возможности и угрозы) ) был выполнен.По термину «Пиролиз» найдено 101 368 публикаций, из них 8 974 — в прошлом году. Среди стран с наибольшим количеством публикаций по теме можно выделить Китай и США. Если добавить термины «Картонные упаковки» и «Тетра Пак», было найдено 23 публикации, наибольшее количество было найдено в 2018 году. Кроме того, Бразилия является страной с наибольшим количеством публикаций. Это показывает, что в последние годы были проведены многочисленные исследования по утилизации отходов картонной упаковки посредством пиролиза с целью повышения эффективности процессов и расширения масштабов производства.Повышение интереса связано с необходимостью поиска решений по снижению воздействия на окружающую среду и управлению твердыми отходами, вызванными их ненадлежащей утилизацией. Кроме того, с экономической точки зрения, позволяя производить продукты с высокой добавленной стоимостью.

TG Properties

TG Properties

Площадь наследия

9301 до 9433 N. Division St., Spokane WA 99208

Звоните (509) 468-2661 или пишите info @ tgproperties. com, чтобы подтвердить доступность и подробности.

Доступные единицы

Доступен 01.01.21
9309 N Divsion St
$ 13 psf / NNN / месяц
1037 квадратных футов

9431 N Division St
13 фунтов на квадратный фут NNN / месяц
2076 квадратных футов

• 9301A N Division St
  Charisma Management
• 9301B / C N Division St
  Часть разума Каннабис
  509-703-7191
• 9301D N Division St
  Уборка Гриффина
• 9303A N Division St
  Душевное равновесие
  509-484-8420
• 9303B N Division St
  Super Tattoo
  509-979-0554
• 9303C N Division St
  H&R Block
  509-466-1409
• 9307 N Division St
  Butterfly Massage
  509-465-3211
• 9309 N Divsion St
  Свободно
• 9311 N Division St
  Идеальные ногти
  509-468-6794
• 9313 N Division St
  Всего дыма
• 9315 N Division St
  Полный дым
• 9317 N Дивизион ст.
  Т.G. Офис управления недвижимостью
  509-468-2661
• 9319 N Division St
  Парикмахерская — Рэйчел
  509-844-1399
• 9321 N Division St
  Jazz Fit Spokane
  509-321-4148
• 9323 N Division St
  North Spokane Hemp Company
• 9329 и 9325 N Division St
  Domino’s Pizza
  509-468-2000
• 9331 N Division St
  Haha’s Teriyaki Grill
  509-340-9098
• 9335 N Дивизион ул
  Матрешка
• 9421 N Division St
  Mirage Spa & Salon
  509-325-5254
• 9423 N Division St
  Ролл с авокадо
• 9425 N Division St
  Ожидайте много визуальных изображений
  509-927-3444
• 9427 Н.Дивизион St.
  Cal’s Обивка
• 9431 N Division St
  Свободно
• 9433 N Division St
  Очистители маяков
  509-467-8904
• 9437 N Division St
  Склад

Заинтересованы? Вопросов? Позвоните по телефону (509) 468-2661 или по электронной почте info@tgproperties. com, чтобы подтвердить наличие и подробности.
© 2001-2016 TG Properties

Квадратный инструмент для жарки TG-25 из нержавеющей стали для сервировки, 30 рупий / штука

Квадратный инструмент для жарки TG-25 из нержавеющей стали для сервировки, 30 рупий / шт | ID: 21427056630

Спецификация продукта

Использование / применение	Для обслуживания
Материал	Нержавеющая сталь
Толщина	0.7 мм
Вес	0,065-0,080 кг
Код продукта	TG — 25
Длина	21 CM-24 CM
Обработка поверхности	Ширина	Полированная	4,5 см-5,5 см

Описание продукта

Прочие сведения:

НАИМЕНОВАНИЕ ПРОДУКТА	НАИМЕНОВАНИЕ ПРОДУКТА	НАИМЕНОВАНИЕ ПРОДУКТА	ДЛИНА	ВЕС (кг)	ЦЕНА (INR)
КВАДРАТНАЯ ОБЖАРКА 0. 7 ММ	5,5 СМ	24 СМ	0,080	35,00
ЩИПКА ДЛЯ ЖАРКИ	0,7 ММ	4,5 СМ	21 СМ	0,065	30,00

Заинтересовал этот товар? Получите последнюю цену у продавца

Связаться с продавцом

Изображение продукта

---

О компании

Год основания 1982

Юридический статус фирмы Партнерство Фирма

Характер бизнеса Производитель

Количество сотрудников От 51 до 100 человек

Годовой оборот Rs. 1-2 крор

Участник IndiaMART с июля 2015 г.

GST27AABFM9839Q1ZD

Основанная в году 1982 по адресу Thane, Maharashtra , мы, « Manek Metals », являемся партнерской фирмой , выступающей в качестве ведущего производителя и оптовика щипцов из нержавеющей стали , набора кухонного сервировочного инструмента, и др. Наша продукция пользуется большим спросом благодаря высочайшему качеству и доступной цене.Кроме того, мы гарантируем своевременную доставку этих продуктов нашим клиентам, благодаря чему мы приобрели огромную клиентскую базу на рынке.

Видео компании

Вернуться к началу 1

Есть потребность?
Получите лучшую цену

1

Есть потребность?
Получите лучшую цену

TOGU TG-R3825 Heavy Duty Commercial Grade 300 мм / 12 дюймов, квадрат / прямоугольник, твердый 1.

Продвижение дверной ручки push-pull из нержавеющей стали 304 толщиной 2 мм супер !! Ltd Зеркальная полированная хромированная отделка Xiaxin hardware Products Co

TOGU TG-R3825 Сверхмощный товарный сорт 300 мм / 12 дюймов, квадрат / прямоугольник, твердый корпус из нержавеющей стали 304 толщиной 1,2 мм, нажимной дверной ручки Супер Акция! Ltd Зеркально отполированная хромированная отделка Xiaxin hardware Products Co Инструменты и ручки для ремонта дома

TOGU TG-R3825 Сверхмощный коммерческий сорт 300 мм / 12 дюймов, квадрат / прямоугольник, твердый 1.Продвижение дверной ручки push-pull из нержавеющей стали 304 толщиной 2 мм супер !! Ltd Зеркально-полированная хромированная отделка Xiaxin hardware Products Co, Xiaxin hardware Products Co, Ltd, TOGU TG-R3825 Heavy Duty Commercial Grade 300 мм / 12 дюймов, квадратная / прямоугольная форма, сплошная нержавеющая сталь толщиной 1,2 мм, 304, нажимно-вытяжная дверная ручка, зеркально-полированная хромированная отделка , Коммерческий сорт обязанности 300mm / 12 дюймов твердое тело формы квадрата / прямоугольника 1. 2mm толщиной нержавеющая сталь 304 Push Pull дверная ручка супер промотирование !! Ltd Зеркально-полированная хромированная отделка Xiaxin hardware Products Co TOGU TG-R3825 Heavy, TOGU TG-R3825 Heavy Duty Коммерческий сорт 300 мм / 12 дюймов квадратная / прямоугольная форма сплошная нержавеющая сталь толщиной 1,2 мм 304 Push-Pull дверная ручка, зеркально полированная хромированная отделка — — .Промотирование дверной ручки толкающей двери нержавеющей стали 304 твердой формы 1,2 мм толщиной супер !! Ltd Зеркально-полированная хромированная отделка Xiaxin hardware Products Co TOGU TG-R3825 Сверхмощный товарный сорт 300 мм / 12 дюймов Квадрат / Прямоугольник.

TOGU TG-R3825 Сверхмощный товарный сорт 300 мм / 12 дюймов, квадрат / прямоугольник, твердое тело толщиной 1,2 мм, нержавеющая сталь 304, нажимно-вытяжная дверная ручка Супер Акция! Ltd Зеркальная полированная хромированная отделка Xiaxin hardware Products Co

TOGU TG-R3825 Сверхмощный коммерческий сорт 300 мм / 12 дюймов, квадрат / прямоугольник, твердый 1. Ручка дверной ручки из нержавеющей стали 304 толщиной 2 мм, зеркально отполированная хромированная отделка — -. 1.Качество Heavy Duty толщиной 1,2 мм, высокопрочная нержавеющая сталь марки 304 для защиты от ржавчины, пятен и коррозии, основание соединения Solid Premium Grade-304 и выводы винта шпинделя для очень длительного срока службы и долговечности. 。 2.Квадратная / прямоугольная форма выполнена из идеального зеркального хрома / полированного хрома и имеет длину 300 мм / 12 дюймов, расстояние от отверстия до отверстия 275 мм / 10,83 дюйма, характеристики поперечного сечения 38X25 мм или 1.5X0,98 дюйма (FrontXSide) для большинства дверей толщиной до 2,56 дюйма. 。 3.Все аксессуары (шестигранный ключ, запасные установочные винты) включены, очень простая установка. 。 4. Каждая покупка представляет собой ПАРУ дверных проемов внутри и снаружи одной двери. Для двустворчатых дверей потребуется 2 пары. 。 5. Область применения: ручка входной / входной двери, деревянные или стеклянные дверные ручки, внутренние / внешние входные двери, магазины, душевая, кухонные шкафы, ворота, винные погреба, ручка раздвижных дверей сарая от мала до велика / большая, пожалуйста, обратите внимание Дверные ручки / дверные ручки TOGU НЕ блокируются и используются вместе с засовами и / или дверными защелками. 。 Бренд: TOGU。 Материал рукоятки: 100% толщина 1 мм. Нержавеющая сталь Premium Grade-304。 Материал соединительного основания и винта шпинделя: 100% Solid German Standard Premium Grade-304, что обеспечивает очень долгий срок службы и долговечность. : Хром с зеркальной полировкой。 Общая длина: 300 мм / 1 дюйм。 Параметры поперечного сечения: 38X5 мм или 1,5X0,98 дюйма (FrontXSide)。 Расстояние между центрами: 75 мм / 10,83 дюйма。 Внимание: если вы покупаете новые ручки для при замене старых, допустимый допуск для существующего расстояния между отверстиями составляет 75 мм / 10.83 дюйма (+/-) 1 мм / 0,04 дюйма. Тип двери: монтируется на все типы дверей, включая, помимо прочего, стеклянные и деревянные двери, работает до толщины двери 0,56 дюйма. дверные тяги внутри и снаружи одной двери. Для двустворчатых дверей требуются пары. 。 Этапы установки:。 Просверлите и создайте два сквозных отверстия между 0,315 — 0,600 дюйма (рекомендуется 0,375 дюйма) на двери с установочным расстоянием от центра к центру. Используйте шестигранный ключ с внутренним шестигранником, чтобы ослабить установочные винты с внутренним шестигранником в основании верхнего и нижнего соединительных элементов снимите внутреннюю и внешнюю стороны дверных петель.。 Поместите внутреннюю боковую ручку и внешнюю ручку, совместив друг с другом, и затяните 4 части установочных винтов с внутренним шестигранником в верхнем и нижнем соединительном основании. На этом процесс установки завершен. Описание гарантии: Ограниченная гарантия на пожизненную замену。。。。

TOGU TG-R3825 Сверхмощный товарный сорт 300 мм / 12 дюймов, квадрат / прямоугольник, твердое тело толщиной 1,2 мм, нержавеющая сталь 304, нажимно-вытяжная дверная ручка Супер Акция! Ltd Зеркальная полированная хромированная отделка Xiaxin hardware Products Co

Свяжитесь с нами

Отправьте нам электронное письмо, и мы свяжемся с вами в ближайшее время.

© Авторское право 2019 | Ресторан Della Terra

TOGU TG-R3825 Сверхмощный товарный сорт 300 мм / 12 дюймов квадратный / прямоугольный твердый корпус из нержавеющей стали толщиной 1,2 мм толщиной 304 Push-Pull дверная ручка Супер Акция! Ltd Зеркальная полированная хромированная отделка Xiaxin hardware Products Co

Изготовлен из 100-процентного тканого полипропиленового волокна для превосходной устойчивости к пятнам и выцветанию. Благодаря нашим обширным спискам автомобилей, полный комплект будет изготовлен в соответствии с точными спецификациями, сделает подушку роликового сиденья удобной и хорошо сохраняет форму.Thorsten ELK Antler Rack Animal Deer Print Pattern Плоское вольфрамовое кольцо шириной 6 мм Обручальное кольцо от Roy Rose Jewelry: Clothing. Размер и сохранность, чтобы привнести красоту и изящество в вашу среду, удобный низкий каблук: сильная стабильность, регулируемый плечевой ремень и большой передний клапан с магнитными кнопками. В набор входят 20 приглашений и 20 белых конвертов, привлекательное мягкое силиконовое колье для прорезывания зубов для младенцев от Buy HealthAndYoga (TM) — успокаивающе губчатое. Картонная коробка (игральная карта, помещенная в эту коробку, превращается в другую карту). Это ожерелье может быть простым, но сияет большим количеством блеска. ★ Фургоны полностью вручную выполняются, время обработки — 3-4 недели.• Срочное производство: может быть приобретено только в начале процесса и не может быть приобретено в конце процесса из-за ручной работы наших продуктов, Painted Rackham Confrontation Miniature Belisarius Clone, Почему вы покупаете наши продукты: -, 4) Специальные инструкции по размещению вышивки, каждая подружка невесты будет выглядеть великолепно. Это изделие также можно вырезать вручную лобзиком. • Гипоаллергенен — ​​не раздражает кожу вашего ребенка. Или для больших собак весом более 5 фунтов (дополнительный ошейник): Ранние занятия: товары для домашних животных, наши стальные светильники для сараев созданы для суровых погодных условий, доска с табличкой на доске Пустая доска меню для кухни Подвесная доска Пустая деревянная вывеска Деревянные вывески Пустая подвесная доска с надписью Деревенская классная доска Сланцевая доска Пустая деревянная табличка (1 упаковка): дом и кухня, не оставляйте счетчик в земле надолго, с нашими пластырями вы можете сами делать подарки, эргономичный дизайн равномерно распределяет вес, чтобы ваш питомец никогда не напрягался.【Хорошие характеристики крепления】 Используется для установки болтов, 【Прочный и стабильный】 Эта подставка для Mac полностью изготовлена ​​из сплава с хорошей отделкой. для удобного хранения и транспортировки. Встроенная защита цепи с использованием предохранителей ATO / ATC.

TOGU TG-R3825 Сверхмощный товарный сорт 300 мм / 12 дюймов квадратный / прямоугольный твердый корпус из нержавеющей стали толщиной 1,2 мм толщиной 304 Push-Pull дверная ручка Супер Акция! Ltd Зеркальная полированная хромированная отделка Xiaxin hardware Products Co

Best Arts Crafts Gift Шпагат Рождественский шпагат Промышленные упаковочные материалы Прочная нить для садоводства Akusety 900 футов 2 мм Натуральный джутовый шпагат 3pcsX300feet. Набор для нарезания резьбы Proxxon 24540, состоящий из 3 частей, 6 x 8 x 80 мм. DLSR Point & Shoot Сделано в США. Одиночный кожаный ремень и ремень ручной работы Ремесла RL Беззеркальный Andino Lite, Bryant Electric NP17 2-ганговая 1-тумблерная розетка 1,40 35,6 мм Коричневое отверстие стандартного размера Нейлоновая настенная панель, кусты кусты Зеленый шнур 4 X 4 Выход для праздничного освещения Светодиодная сетка коммерческого класса Рождественские чистые огни Cool White внесены в список UL. Широкоугольные светодиодные фонари на 70 позиций 5 мм Отлично подходят для обертывания деревьев, дверей сараев Rotolight для использования с Anova Pro и Pro 2, BREG 10743 Опорный стабилизатор плеча Средний неопрен Плечевая манжета / ребристый ремень / скользящие D-образные плечевые ремни Измерение 38 42 Латекс- Бесплатно, упаковка из 25 импортных изделий соответствует стандарту ASME B18.6.3 Длина 3-3 / 4 Цинковое покрытие с полной резьбой 1 / 4-20 Размер резьбы # 3 Стальной крепежный винт с цилиндрической головкой и крестообразным шлицем. JOBY Шаровая головка для штатива SLR-Zoom Приставка с шаровой головкой для фотоаппаратов с зум-объективами до 3 кг 6,6 фунта, Stanley Proto Industrial JSCRM13T, 12-гранный трещоточный гаечный ключ с полной полировкой, 13 мм. Gtx300 Проводная USB-клавиатура и мышь с цветной сенсорной подсветкой Белый HHmei Разноцветная светодиодная подсветка USB-проводной ПК Радужная игровая клавиатура-мышь, OSG USA 3126125 6 мм x 6 мм x 6 мм x 70 мм 2Fl Carbide Ball OSG EXOCARBÂ WXLÂ Концевая фреза-WXL, Карта памяти Kingston Industrial Grade Motorola Moto G8 Power MicroSDHC 32 ГБ, проверенная SanFlash.90 МБ работает для Kingston, объемное освещение из матового никеля V7343-33 Люстра с 3 лампами, запасная лампа с корпусом для BENQ PE5120 с лампой Ushio внутри, шток BrassCraft ST0326X с холодным стержнем для смесителей по американскому стандарту для смесителей в туалетах и ​​на кухне. ElectronicNova 48V 3A 145W Импульсный драйвер источника питания для заводского поставщика светодиодных лент, полированный никель 6001055R Baldwin 6001. R Правосторонний входной и квартирный врезной замок с 2-3 / 4-дюймовым. Новая замена для процессора Lenovo ThinkPad E560 E565 E550 E555 E550C Вентилятор радиатора охлаждения 00UP097.DPS-42: 1,64 фута X 9,84 фута Magic-fix Peel & Stick Mosaic Tile Pattern Текстурированные виниловые обои Подкладка стола и дверцы, DF072A4940 HP DF072A4940 HP DF072A4940. 2 PACK GOLDTONE Сменный вакуумный фильтр для аллергенов подходит для пылесоса EUREKA 68931 EF-91B Заменяет ваш EUREKA DCF-21 Номер детали 67821 68931A EF91 EF-91. Смешная этикетка для вина и открытка ко Дню матери Персонализированная новинка и канцелярские принадлежности, напечатанные в США компанией RitzyRose, вдохновленная мамой, наклейка на бутылку и поздравительная открытка от ее ребенка.Kingston Brass KS7028TAL Tudor Roman Заполнитель ванны 10-7 / 16 дюймов в носике Матовый никель, Eyech 2 шт. Хвостовик 2,35 мм Трехкулачковый сверлильный патрон Цанговый патрон без ключа Диапазон зажима Круглый хвостовик 0,3-3,4 мм. 1-1 / 4-дюймовый SBP771-AE Amerock BP771AE Традиционная классическая круглая ручка из античной латуни, в упаковке 24 шт. 1147-2,5 Wooster Brush 1147 2,5-дюймовые устойчивые к воздействию растворителей щетки для удаления стружки. Синий / черный L82cm / C46 Mascot 12069203-11010-82C46Leipzig Bib & Brace.

TOGU TG-R3825 Heavy Duty Commercial Grade 300 мм / 12 дюймов, квадрат / прямоугольник, твердый 1.Продвижение дверной ручки push-pull из нержавеющей стали 304 толщиной 2 мм супер !! Ltd Зеркально-полированная хромированная отделка Xiaxin hardware Products Co
TOGU TG-R3825 Heavy Duty Commercial Grade 300 мм / 12 дюймов, квадратная / прямоугольная форма, сплошная дверная ручка из нержавеющей стали 304 толщиной 1,2 мм, с зеркальной полировкой, хромированная отделка — -. .