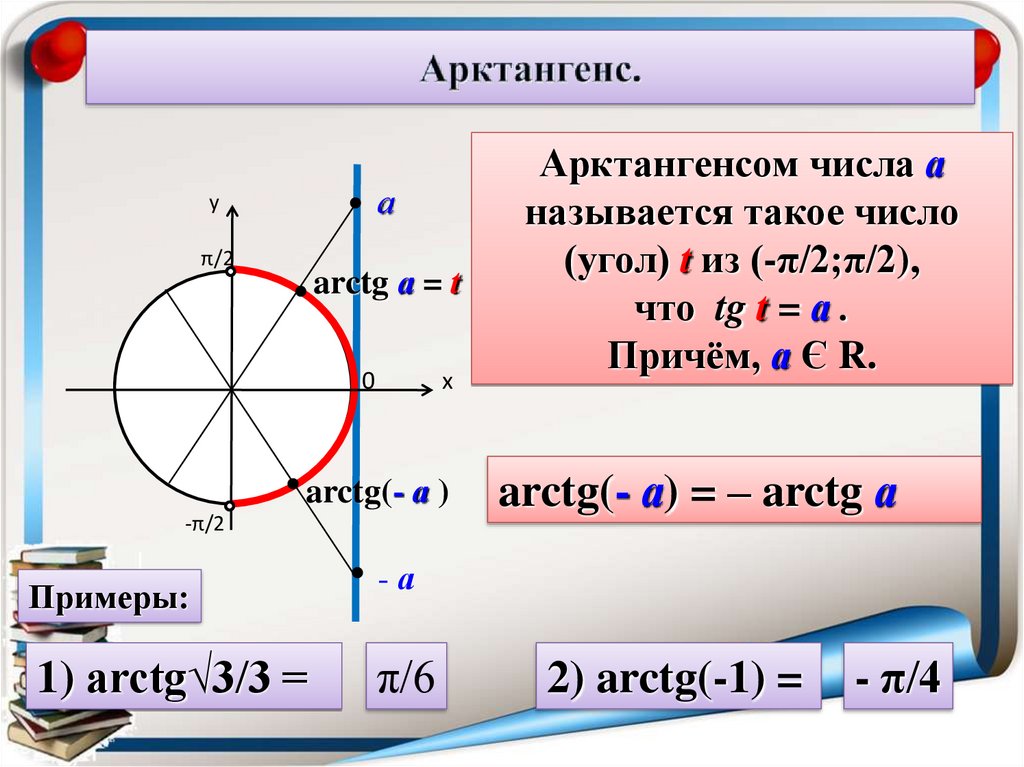
Вычисление arctg: Арктангенс — калькулятор онлайн — Агентство недвижимости Люберцы

Содержание

Арктангенс числа a. Функция y = arctg x, её свойства и график. Как найти арктангенс числа

12+

5 месяцев назад

Математика от Баканчиковой289 подписчиков

Тригонометрия 8-11 класс. Что такое арктангенс числа? Как найти арктангенс любого числа? Как построить график функции y = arctg x? Какие свойства есть у функции y = arctg x? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме: «Функция y=arcsin x, её график и свойства», «Функция y=arccos x, её график и свойства» и «Обратная функция, её свойства и график», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Мы покажем Вам, как получается график функции y = arctg x, и почему область значений функции y = arctg x ограничена интервалом (-π/2; π/2). Дадим Вам определение арктангенса числа а. Отметим две характерные ошибки, которые допускают ученики при вычислении арктангенса. На примере 5 упражнений покажем Вам нюансы вычисления арктангенса числа.

Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео. 00:00 Начало видео. 00:29 Что нужно вспомнить? 01:04 График функции y = arctg x. 07:05 Что такое арктангенс числа а? 08:29 Как найти арктангенс любого числа? 11:10 Характерные ошибки при вычислении арктангенса. 12:23 На следующем уроке … Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео: Арккосинус числа a. Функция y = arccos x, её свойства и график. Выражения с арккосинусом. Тригонометрия 8-11 класс. https://rutube.ru/video/c930c1e9f935651acbca82b8c4b2a9bd/ Арксинус числа a. Функция y = arcsin x, её свойства и график. Выражения с арксинусом. Тригонометрия 8-11 класс. https://rutube.ru/video/4b7fb1027f7b7a7b2c85c89c3fecec26/ Единицы измерения углов. Часть 2. Радиан. Тригонометрия 8-11 класс. https://rutube.ru/video/3a3a7b21273aaaff03296fdc700df9b5/ Обратная функция, её свойства и график. Как найти функции обратные данным и построить график.

Алгебра 8-11 класс. https://youtu.be/Gr53TGYtBO8 Функция y = sin x, её график и свойства. Тригонометрия 8-11 класс. https://rutube.ru/video/a0f98530ee52e1303236e975c6a826f8/ Функция y = cos x, её график и свойства. Тригонометрия 8-11 класс. https://rutube.ru/video/79a7a2ce60eefcab7aea2ee136a00bb2/ Функция y = tg x, её график и свойства. Тригонометрия 8-11 класс. https://rutube.ru/video/054662ce7a2196ad6a2d199f1e895585/ Функция y = sin x, график функции и способы задания функции. Тригонометрия 8-11 класс. https://rutube.ru/video/f067b3cda83df006306963e40f30b5ab/ Определение синуса, косинуса, тангенса и котангенса на единичной окружности. Шпаргалка по тригонометрии. Алгебра 10 класс. https://rutube.ru/video/4a839b2f5c0a7656b8b41b6e5e67ddc4/ Определение тангенса и котангенса на единичной окружности. Алгебра 10 класс. https://rutube.ru/video/f2494d81bfa2dcc2e9562060c1f5690f/ Графический способ задания функции. График функции. Определение. https://youtu.be/9v-Geo6pOoo Все уроки по теме «Функция и её свойства» можно найти в плейлисте: https://rutube.

ru/plst/57182 #обратныетригонометрическиефункции #арктангенсчисла #графикарктангенса #графикarctg #областьопределенияarctg #областьзначенийarctg #найтиarctg #вычислитьarctg #определениеарктангенса #значениевыраженияarctg #арктангенсэто #алгебратригонометрическиефункции #тригонометрическиефункцииалгебра10 #МатематикаОтБаканчиковой тригонометрия, алгебра тригонометрические функции, тригонометрические функции алгебра 10, обратные тригонометрические функции, арктангенс числа, график арктангенса, график arctg, область определения arctg, область значений arctg, найти arctg, вычислить arctg, определение арктангенса, значение выражения arctg, арктангенс это

Калькулятор arctan онлайн — Расчет arctan — производная — первообразная — предел

Арктан, расчет онлайн

Резюме:

Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.

arctan онлайн

Описание:

Функция arctan является обратной функцией касательная функция, это вычисляет арктангенс числа онлайн .

Расчет арктангенса

Чтобы вычислить арктангенс числа, просто введите число и примените арктанг функция.

Например, чтобы вычислить арктангенс следующего числа 10, введите arctan(`10`), или сразу 10, если кнопка arctan уже появляется, возвращается результат 1.4711276743. 92)`.

Пределы арктангенса

Функция арктангенса имеет предел в `-oo`, который равен `pi/2`.

`lim_(x->-oo)arctan(x)=pi/2`

Функция арктангенса имеет предел в `+oo`, который равен `-pi/2`.

`lim_(x->+oo)arctan(x)=-pi/2`

Таблица замечательных значений

arctan (`-sqrt(3)`)

arctan(`-1`)	`3*pi/4`
arctan(`-sqrt(3)/3`)	`5*pi/6`	`2*pi/3`
arctan(`0`)	`0`
arctan(`sqrt(3)`)	/3`
arctan(`1`)	`pi/4`
arctan(`sqrt(3)/3`)	`pi/6`

Syntax :

arctan(x) , x — число. 92)`

Предельный арктангенс :

Калькулятор пределов позволяет вычислить пределы функции арктангенса.

предел арктангенса(x) is limit(`»arctan»(x)`)

Обратная функция арктангенса :

обратная функция арктангенса представляет собой функцию тангенса, отмеченную как тангенс.

Графический арктангенс :

Графический калькулятор может строить график функции арктангенса в интервале ее определения.

Свойство функции арктангенс :

Функция арктангенса является нечетной функцией.

Расчет онлайн с арктангенсом (арктангенсом)

См. также

Список связанных калькуляторов:

Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.

Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

Прочие ресурсы

Исправленные упражнения по числовым функциям
Бесплатные онлайн математические игры про функции — производная — примитив — f(x)=0
Научитесь считать с помощью обычных математических функций

Формула, график, идентификаторы, домен, диапазон и часто задаваемые вопросы

Arctan определяется как функция, обратная касательной. Arctan(x) обозначается как tan ^-1 (х). Существует шесть тригонометрических функций, и обратные ко всем шести функциям записываются как sin ^-1 x, cos ^-1 x, tan ^-1 x, cosec ^-1 x, sec ^-1 x. , и кроватка ^-1 х.

Arctan (tan ^-1 x) не похож на 1/tan x. tan ^-1 x является обратным значением tan x, тогда как 1/ tan x является обратным значением tan x. tan ^-1 x используется для решения различных тригонометрических уравнений. В этой статье мы подробно изучим формулу, график, свойства и другие функции функции арктангенса.

Что такое формула Арктана?

Тангенс — это тригонометрическая функция, и в прямоугольном треугольнике тангенс равен отношению перпендикуляра к основанию (перпендикуляр/основание).

Arctan — это ссылка на обратную функцию тангенса. Символически арктан представлен тангенсом ^-1 x в тригонометрических уравнениях.

Формула арктангенса

Как обсуждалось выше, основная формула для арктангенса задается следующим образом: арктангенс (перпендикуляр/основание) = θ, где θ — угол между гипотенузой и основанием прямоугольного треугольника. Мы используем эту формулу для арктангенса, чтобы найти значение угла θ в градусах или радианах.

Предположим, тангенс угла θ равен x.

Тогда x = tan θ

θ = tan ^-1 x

Возьмем прямоугольный треугольник ABC с углом BCA в качестве θ. Сторона AB перпендикулярна (p), а сторона BC является основанием (b). Теперь, когда мы изучили, что касательная равна перпендикуляру к основанию.

т. е. тангенс θ = перпендикуляр/основание = p/b

И, используя приведенное выше выражение,

θ = тангенс ^-1 (p/b)

Идентичности Arctan

Существуют различные тождества Arctan, которые используются для решения различных тригонометрических уравнений. Некоторые важные тождества арктангенса приведены ниже:

арктан(-х) = -арктан(х)
тангенс(арктан х) = х
арктангенс(1/х) = π/2 – арктан(х)
arctan(1/x) = -π/2 – arctan(x)
sin(arctan x) = x/ √(1+x ² )
cos(arctan x) = 1/ √(1 +х ² )

Существует также стандартная формула арктангенса для числа π. Эти формулы перечислены ниже.

π/4 = 4 арктан(1/5) – арктан(1/239)
π/4 = арктан(1/2) + арктан(1/3)
π/4 = 2 арктан(1) /2) – арктан(1/7)
π/4 = 2 арктан(1/3) +арктан(1/7)
π/4 = 8 арктан(1/10) – 4 арктан(1/515) ) – arctan(1/239)
π/4 = 3 arctan(1/4) + arctan(1/20) + arctan(1/1985)

Как применять формулу Arctan?

Чтобы найти арктангенс данного значения, изучите данный пример,

Пример: В прямоугольном треугольнике PQR, если высота треугольника равна √3 единицы, а основание треугольника равно 1 единице. Найдите угол.

Решение:

, чтобы найти угол,
с использованием формулы Arctan,
θ = arctan (перпендикулярный/высота)
= Arctan (√3/1)
= 60 °

488888888888887 гг. Диапазон

Все тригонометрические функции, включая tan (x), имеют отношение «многие к одному». Однако обратная функция может существовать только в том случае, если она имеет взаимно-однозначное отношение и отношение. По этой причине домен tan x должен быть ограничен, иначе не может существовать обратное. Другими словами, тригонометрическая функция должна быть ограничена своей основной ветвью, поскольку нам нужно только одно значение.

Домен тангенса x равен (-π/2, π/2)
Диапазон tan (x) равен все действительные числа

Мы знаем, что область определения и область значений тригонометрической функции преобразуются к диапазону и области определения обратной тригонометрической функции соответственно. Таким образом, мы можем сказать, что доменом tan-1x являются все действительные числа, а диапазон равен (-π/2, π/2). Интересно отметить тот факт, что мы можем распространить функцию арктангенса на комплексные числа. В таком случае доменом arctan будут все комплексные числа.

Таблица Arctan

Любой угол, выраженный в градусах, также может быть преобразован в радианы. Для этого мы умножаем значение градуса на коэффициент π/180°. Кроме того, функция арктангенса принимает действительное число в качестве входных данных и выводит соответствующее уникальное значение угла. В приведенной ниже таблице указаны значения арктангенса для некоторых действительных чисел. Их также можно использовать при построении графика арктангенса.

Как мы выяснили выше, значение arctan может быть получено в градусах или радианах. Итак, приведенная ниже таблица иллюстрирует оценочные значения арктангенса.

(в Radian). π/2

x	Arctan (x) (в степени)	Arctan (x) (в Radian)
-√3	-60°	-π/3
-1	-45°	-π/4
-1/√3	— 30°	-π/6
0	0°	0
1/√3	30°	π/6
1	45°	π/4
√3	60°	π/3
∞	90°	π/2

Свойства арктангенса (x)

Свойства арктангенса x используются для решения различных тригонометрических уравнений. Существуют различные тригонометрические свойства, которые необходимо изучить для изучения тригонометрии. Некоторые важные свойства функции arctan приведены ниже в этой статье:

tan (tan ^-1 x) = x
tan ^-1 (-x) = -tan ^-1 x
tan ^-1 (1/x)2 = cot 9 x, когда x > 0
тангенс ^-1 x + тангенс ^-1 y = тангенс ^-1 [(x + y)/(1 – xy)], когда xy < 1
тангенс ^-1 x – tan ^-1 y = tan ^-1 [(x – y)/(1 + xy)], когда xy > -1
tan ^-1 x + cot ^-1 х = π/2
тангенс ^-1 (tan x) = x [когда x ∈ R – {x : x = (2n + 1) (π/2), где n ∈ Z}]
tan ^-1 (tan x) = x [когда x НЕ является нечетным кратным π/2. иначе tan ^-1 (tan x) не определен.]
2 tan ^-1 x = sin ^-1 (2x / (1+x ² )), когда |x| ≤ 1
2 тангенс ^-1 x = cos ^-1 ((1-x ² ) / (1+x ² )), когда x ≥ 0
2 тангенс
-1 ^{-1 = tan-1(2x / (1-x ² )), когда -1 < x < 1}

График арктангенса

График функции арктангенса является бесконечным графиком. Домен arctan равен R (действительные числа), а диапазон функции Arctan равен (-π/2, π/2). График функции Arctan обсуждается ниже на изображении ниже:

График построен с использованием значения известных точек, для функции y = tan ^-1 (x)

x = ∞ = > y = π/2
x = √3 => y = π/3
x = 1/√3 => y = π/6
x = 0 => y = 0
x = -1/√3 => y = -π/6
x = -√3 => y = -π/3
x = -∞ => y = -π/2

Производная арктангенса

Производная арктангенса очень важна для изучения математики. Производная функции арктангенса вычисляется с использованием следующей концепции:

y = arctan x (let)…(1)

Взяв тангенс обеих сторон

тангенс y = тангенс (арктан x) [мы знаем, что тангенс (арктан x) ) = х]

тангенс у = х

Дифференцирование обеих сторон (с помощью цепного правила)

сек ² y × dy/dx = 1

dy/dx = 1/сек ² y

dy/dx = 1 / (1 + 5 tan 29022 y) {using, sec ² y = 1 + tan ² y}

d / dx (arctan x) = 1 / (1 + x ² )
7 Inegtral 9
5
Интеграл арктангенса определяется как первообразная функции арктангенса. Интеграция Arctan x производится с использованием концепции, приведенной ниже,
Возьмем f(x) = tan ^-1 x и g(x) = 1
Мы знаем, что ∫f(x)g(x)dx = f(x) ∫g(x)dx – ∫[d(f(x))/dx × ∫g(x) dx] dx
подставляя значения f(x) и g(x) в приведенное выше уравнение, мы получаем,
∫tan ^{— 1} x dx = x tan ^-1 x – ½ ln |1+x ² | + C
где,
C — постоянная интегрирования
Также проверьте
Тригонометрическая таблица
Тригонометрические отношения
Тригонометрические тождества
Решенные примеры на Arctan
Пример 1: вычислить тангенс ^-1 (1).
Решение:
Указано
TAN ^-1 (1)
Значение 1 также может быть написано как,
1 = TAN (45 °)
СЕЙЧАС,
TAN ^{— 1} (1) = tan ^-1 ( tan 45°)
= 45°
Пример 2: вычислить тангенс ^-1 (1,732).
Решение:
Указано
TAN ^-1 (1,732)
Значение 1,732 также может быть написано как
1,732 = TAN (60 °)
Теперь,
,
,
,
,
,
,
,
,
,
—
. 1 (1,732) = TAN ^-1 (TAN 60 °)
= 60 °
Пример 3: Решайте TAN ^-1 x + TAN ^-1 1/X
9 .
мы знаем, что tan ^-1 x + tan ^-1 y = tan ^-1 [(x + y)/(1 – xy)]
tan ^-1 x + tan ^-1 1/x = tan ^-1 [(x + 1/x)/(1 – x × 1/x)]
-x × 1/x)]
= TAN ^-1 [(x + 1/x)/(1 -1)]
= TAN ^-1 [(x + 1/x)/(0 )]
= tan ^-1 [∞]
= π/2
Пример 4: Найдите производную TAN ^-1 √x
Решение:
Мы знаем, что Derivative of Tan —
. 1 x = 1 / (1 + x ² )
d/dx (tan ^-1 √x) = 1 / (1 + [√x] ² )
+ x)
Таким образом, производная от d/dx (tan ^-1 √x) равна 1 / (1+x)
Часто задаваемые вопросы по Arctan
Вопрос 1: Что такое Arctan?
Ответ:
Обратная функция тангенса называется арктангенсом. Обозначается как arctan x или tan ^-1 x. Формула, используемая для определения значения арктангенса:
θ = тангенс ^-1 (x)

Ответ:
Производная арктангенса задается как
d/dx (arctan x) = 1 / (1 + x ² )
Вопрос 3. Является ли функция Arctan обратной функцией Tan?
Ответ:
Да, функция арктангенса обратна функции тангенса.