Опубликовано Сложение и вычитание дробей
Репетиторы ❯ Математика ❯ Сложение и вычитание дробей
Автор: Валентин В., онлайн репетитор по математике
●
05.10.2011
●
Раздел: Математика
Сложение и вычитание дробей с одинаковым знаменателем отличается от сложения и вычитания дробей с разным знаменателем.
Если мы складываем / вычитаем дроби с одинаковым знаменателем, то:
1. производим требуемую вычислительную операцию с числителем;
2. знаменатель оставляем тем же.
Решим пример 5/6 – 2/6 = ?
1. Выполняем вычитание в чилителе: 5 – 2 = 3.
2. Знаменатель оставляем прежним, т.е. 6, следовательно, мы получаем дробь 3/6. Это и есть наш ответ.
НО! Нашу дробь можно сократить на 3: делим и числитель, и знаменатель на 3 и получаем 3/6 = 1/2.
Запишем полное решение нашего примера: 5/6 – 2/6 = (5 – 2)/6 = 3/6 = 1/2.
Чтобы сложить или вычесть дроби с разными знаменателями, нужно:
1. привести дроби к общему знаменателю;
2. сложить / вычесть получившиеся дроби с одинаковым знаменателем.
Как видим, сложение и вычитание дробей с разными знаменателями сводится к операциям с дробями с одинаковыми знаменателями.
Рассмотрим пример: 3/10 + 4/15.
1. Наши дроби имеют разные знаменатели, поэтому приведем их к общему знаменателю. И 10, и 15 являются делителями числа 30, которое и будет нашим общим знаменателем. Чтобы привести наши дроби к общему знаменателю 30, первую дробь (и числитель, и знаменатель) нам нужно домножить на 3, а вторую (и числитель, и знаменатель) – на 2.
2. Складываем дроби с одинаковыми знаменателями: 9/30 + 8/30 = (9 + 8)/30 = 17/30. Итак, наш ответ 17/30.
Запишем решение примера:
3/10 + 4/15 = 3 ∙ 3/10 ∙ 3 + 4 ∙ 2/15 ∙ 2 = (9 + 8)/30
(9 + 8)/30 = 17/30.
Решим пример 3/8 + 1/4 = ?
1. Наши дроби имеют разные знаменатели, поэтому приведем их к общему знаменателю. И 8, и 4 являются делителями числа 8, которое и будет нашим общим знаменателем. Чтобы привести наши дроби к общему знаменателю 8, первую дробь (и числитель, и знаменатель) нам нужно домножить на 1 (она остается в первоначальном виде), а вторую (и числитель, и знаменатель) – на 2. Получаем: 3/8 + 1 ∙ 2/4 ∙ 2 = 3/8 + 2/8.
2. Складываем дроби с одинаковыми знаменателями: 3/8 + 2/8 = (3 + 2)/8 = 5/8. Итак, наш ответ 5/8.
Запишем решение примера: 3/8 + 1/4 = 3/8 + 1 ∙ 2/4 ∙ 2 = 3/8 + 2/8 = (3 + 2)/8 = 5/8.
Основные законы сложения – переместительный, сочетательный и распределительный – также актуальны и при сложении и вычитании дробей.
Пример 1.
Найдем значение выражения 5 – 4/9.
Решение.
1. Чтобы облегчить вычисления представим 5 как сумму 4 + 1. Наше выражение примет вид: 4 + 1 – 4/9.
2. Для удобства вычисления и используя наши законы, вычтем 4/9 из 1 (представим ее как 9/9) и прибавим к 4, т.е. выражение примет вид: 4 + (9/9 – 4/9).
3. Находим значение: 4 + (9/9 – 4/9) = 4 + 5/9 = 4 5/9.
Ответ: 4 5/9.
Пример 2.
Найдем значение выражения 3 – 1 3/7.
Решение.
1. Чтобы облегчить вычисления представим 1 3/7 как сумму 1 + 3/7. Наше выражение примет вид: 3 – (1 + 3/7).
2. Раскроем скобки нашего выражения: 3 – (1 + 3/7) = 3 – 1 – 3/7.
3. Для удобства вычисления и используя наши законы, вычтем 3 – 1, а затем от результата вычтем 3/7, т.е. выражение примет вид: (3 – 1) – 3/7.
4. Находим значение: (3 – 1) – 3/7 = 2 – 3/7 = 1 4/7.
Ответ: 1 4/7.
Пример 3.
Найдем значение выражения 2 3/5 + 1 1/4.
Решение.
1. Для удобства вычисления сложим целые части и дроби по отдельности, сгруппировав их.
Выражение примет вид: 2 + 1 + 3/5 + 1/4 = 3 + 3/5 + 1/4.
2. Чтобы сложить наши дроби, нам нужно привести их к общему знаменателю. Общий знаменатель для наших дробей – 20. Значит, первую дробь мы домножим на 4, а вторую на 5 и получим: 3 ∙ 4/5 ∙ 4 + 1 ∙ 5/4 ∙ 5 = 12/20 + 5/20 = 17/20.
3. Таким образом, наше выражение примет вид: 3 + 17/20 = 3 17/20.
Ответ: 3 17/20.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
Онлайн Тренажер ДРОБИ.
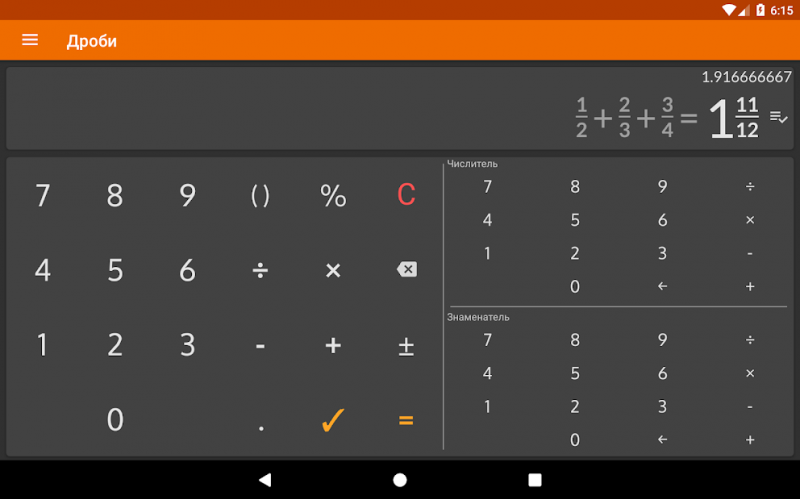Сложение, Вычитание, Умножение и Деление ⏳Менталар представляет вам бесплатно онлайн тренажер Дроби.
Тренажер дроби для любого класса
Данный тренажер подходит для изучения и закрепления дробей в игре — начиная с 2 класса по изучению этой темы
3 класса , 4 класса, 5 класса, 6 класса дроби, 7 класса , 8 класса, 9 класса, 10 класса, 11 класса
Что такое дроби?
Дробное число или дробь используется для представления сегмента целого числа.
Дробь будет состоять из двух чисел, расположенных одно над другим. Первое число, которое находится над строкой, является числителем . Второе число под линией — знаменатель .
Знаменатель указывает общее количество равных частей, на которые что-то делится. Числитель показывает, сколько из этих равных частей необходимо учитывать.
Самый простой способ запомнить дроби — это обозначить линию, разделяющую каждое число, «вне». Таким образом, дробь, записанная как 3/5, просто относится к 3 частям из 5 равных частей.
Упрощение дробей Тренажер
Первый метод — разделить верхнюю и нижнюю части дроби поровну на целые числа больше 1, пока вы не сможете продолжить. В качестве примера возьмем дробь 24/108:
- Разделите каждое число на 2, чтобы получить 12/54.
- Снова разделите на 2, чтобы получить 6/27.
- Разделите на 3, чтобы получить 2/9
Добавление дробей Тренажер
Чтобы сложить дроби, вам нужно изменить их так, чтобы знаменатели (нижние числа) были одинаковыми. Затем вы суммируете числители.
Дополнение: Пример 1
Допустим, вы хотите добавить ¼ к ¼.
Знаменатели уже те же, поэтому вы можете перейти ко второму шагу и прибавить 1 к 1.
Дополнение: Пример 2
Допустим, вы хотите сложить дроби и ⅙.
Чтобы знаменатели совпали, измените ⅓ на 2/6.
Добавьте 1 к 2, чтобы получить 3, и поместите 6 ниже. Ответ — 3/6. Упростите это до ½.
Вычитание дробей по тренажеру
Вычитание дробей работает аналогичным образом:
- Шаг 1.
- Шаг 2 — вычтите числители
- Шаг 3 — При необходимости упростите дробь
Вычитание: пример 1
Допустим, вас попросили потренироваться ¾ — ¼
Первый шаг относительно прост, потому что числа совпадают.
Второй шаг включает в себя вычитание первых чисел и затем перенос ответа над тем же знаменателем.
Таким образом, ¾ — be будет обработано как 3-1 = 2
Следовательно, ответ будет 2/4, что составляет ½.
Умножение дробей Тренажер
Умножение дробей относительно легко; вы просто перемножаете верхние числа и нижние числа.
Если, например, вы умножите дроби ½ и ⅓, вы получите. От вас не ждут, что вы найдете общий знаменатель путем умножения.
Деление дробей Тренажер
Чтобы разделить дроби, вам нужно перевернуть дробь, которую вы делите, вверх дном. Например, если вы хотите разделить ½ на, вы переписываете уравнение так, чтобы вторая дробь была 3/1. Затем умножьте ½ на 3/1, и вы получите 3/2.
Может потребоваться дальнейшее уменьшение фракции для достижения сложной фракции.
Исследуй дальше Обратные Числа
Распространенные ошибки и на что следует обратить внимание. Тренажер
Давайте возьмем пример, сложив вместе ¾ и ⅙.
Первое, что нужно сделать, это получить одинаковые знаменатели, поэтому мы умножаем их, чтобы получить 24.
Мы умножили знаменатель 4 на 6, чтобы получить 24, поэтому мы также умножаем числитель на 6, чтобы получить 18/24.
Мы умножили знаменатель 6 на 4, чтобы получить 24, поэтому мы также умножаем числитель на 4, чтобы получить 4/24.
Теперь мы можем просто добавить 18/24 к 4/24, чтобы получить 22/24, что упрощается до 11/12.
Другие распространенные ошибки включают:
Оставляйте знаменатель неизменным во время вопросов, касающихся умножения или сложения.
Как неправильную дробь перевести в смешанное число. Тренажёр
Любую неправильную дробь можно превратить в смешанную.
Для этого нужно выделить из нее целую часть.
Чтобы из неправильной дроби выделить целую часть, нужно:
разделить с остатком числитель на знаменатель;
частное без остатка будет целой частью;
остаток (если он есть) дает числитель дробной части, а знаменатель дробной части остается тем же, что и у неправильной дроби.
Тренажёр по этой теме поможет вам закрепить эту тему.
Как смешанное число перевести в неправильную дробь Тренажёр
Рассмотрим как любую смешанную дробь можно перевести в неправильную. Для этого целую часть умножают на знаменатель и прибавляют числитель дробной части. Полученную сумму берут числителем, а знаменатель оставляют тот же, например:
Тренажёр и тест помогут вам закрепить эту тему.
Умножение и деление десятичных дробей Онлайн тренажер
Давайте проверим себя, как вы умеете умножать и делить десятичные дроби. Вспомните, как нужно умножать и делить дроби, а затем поработайте на нашем тренажёре. В нём всего 21 пример, но будьте внимательны!
Задания в тренажёре включают умножение и деление на 0,1; 0,01; 0,001; 0,0001 и т.
д, а также умножение и деление десятичных дробей на 10, 100, 1000 и т.д. То есть мы учимся правильно переносить запятую.
Как умножать десятичные дроби на 10, 100, 1000, 10 000 и т. д?
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
Например:
8,963 · 10 = 89,63
0,062 · 1000 = 0062 = 62 (нули перед числом не пишутся)
2,9 · 10000 = 2,9000 · 10000 = 29000
Как умножать десятичные дроби на 0,1; 0,01; 0,001 и т.д?
Умножить число на 0,1; 0,01; 0,001 и т.д. — это то же самое, что разделить его на 10, 100, 1000 и т.д. Для этого нужно перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит перед единицей в множителе (нуль перед запятой тоже считаем).
Например:
54,3 · 0,1 = 54,3 : 10 = 5,43
0,1 · 0,01 = 0,1 : 100 = 000,1 : 100 = 0,001
Как делить десятичные дроби на 0,1; 0,01; 0,001 и т.д?
Разделить число на 0,1; 0,01; 0,001 и т.
д. — это то же самое, что умножить его на 10, 100, 1000 и т.д. Для этого нужно перенести запятую в делимом на столько знаков вправо, сколько нулей стоит в делителе перед единицей (ноль перед запятой тоже считаем).
Если цифр не хватает, надо сначала приписать в конце дроби несколько нулей.
Например:
54,87 : 0,1 = 548,7
34,56 : 0,0001 = 34,5600 : 0,0001 = 345600
24 : 0,001 = 24,000 : 0,001 = 24000
Как делить десятичные дроби на 10, 100, 1000 и т.д?
Для того, чтобы разделить десятичную дробь на 10, 100, 1000, …, надо перенести запятую в этой дроби на столько знаков влево, сколько нулей стоит после единицы в делителе.
При этом иногда приходится сначала написать перед целой частью нуль или несколько нулей.
Например:
374,5 : 100 = 3,745
5,021 : 1000 = 0005,021 : 1000 = 0,005021
0,1 : 100 = 000,1 : 100 = 0,001
В этом онлайн тренажере необходимо выбрать правильный ответ и нажать на него. В случае правильного ответа он загорится зеленым цветом, если ответ неверный — красным.
В этом случае попробуйте найти правильный ответ, а затем нажмите кнопку «Дальше».
Онлайн тренажер по математике из раздела «Умножение и деление десятичных дробей»
Закрепляющие файлы для работы.
Менталар желает Вам легкой плодотворной усвояемой работы над собой.
Верьте в себя и у вас все получится!!!
Ваш сайт Менталар.
Калькулятор дробей — множитель дробей, сложение
Калькулятор дробей
Что такое дробь? Части и значение
Дробь в самом простом значении этого слова относится к количеству, которое не является целым, таким образом выражая отношение часть-целое. С точки зрения математики дробь представляет собой количество частей целого. Итак, если мы представим 7 частей целого, состоящего из 10 частей, то дробь будет представлена как 7 ÷ 10.
Дробь представлена в терминах части и целого, разделенных линией деления. Математическая дробь также имеет 2 части:
- Числитель: появляется в верхней части линии деления и представляет часть.
- Знаменатель: появляется под чертой деления и представляет собой целое, частью которого является числитель.
Например, в дроби 2 ÷ 7 2 — числитель, а 7 — знаменатель.
Типы дробей
В математике дроби могут быть 6 основных типов, в которых категории не являются исключительными (т. е. конкретная дробь может попадать более чем в одну категорию).
- Правильная дробь
Правильная дробь – это дробь, у которой числитель меньше знаменателя. Так, 8 ÷ 17, 2 ÷ 5, 1 ÷ 5 и т. д. — все это примеры правильных дробей в качестве их числителей, т. е. числа над чертой деления (8, 2, 1) меньше знаменателей, т. е. числа, выраженные ниже линия разделения (17, 5, 5).
- Неправильная дробь
Неправильной дробью называется дробь, в которой знаменатель меньше числителя (и наоборот, числитель больше знаменателя). Так, например, примеры неправильных дробей включают 8 ÷ 5, 4 ÷ 3, 3 ÷ 2.
- Одинаковые дроби
Одинаковые дроби состоят из пары дробей с одинаковым знаменателем.
Такие операции, как сложение и вычитание, можно выполнять непосредственно над одинаковыми дробями. Так, например, 49 и 79 похожи на дроби. Точно так же 3 ÷ 5 и 2 ÷ 5 также похожи на дроби - В отличие от дробей
В отличие от дробей относятся к паре дробей, в которых знаменатели различны. Чтобы выполнять такие действия, как сложение и вычитание над неправильными дробями, их нужно сначала преобразовать в одинаковые дроби. Например, 4 ÷ 9и 5 ÷ 8 являются парой непохожих дробей, так как их знаменатели (9 и 8) различны и не равны.
Во многих математических операциях вам может понадобиться преобразовать неправильную дробь в правильную дробь. Вот как это сделать:
Такие операции, как сложение и вычитание, можно выполнять непосредственно над одинаковыми дробями. Так, например, 49 и 79 похожи на дроби. Точно так же 3 ÷ 5 и 2 ÷ 5 также похожи на дробиВо-первых, найдите наименьшее общее кратное (НОК) дробей. Например, для 4 ÷ 6 и 5 ÷ 8 знаменатели равны 6 и 8, а НОК 6 и 8 равен 24.
вам придется умножить знаменатели, чтобы получить LCM. (Легкий трюк — разделить НОК на знаменатель). Например, в случае числа 8 его нужно умножить на 3, чтобы получить 24, а в случае 6 его нужно умножить на 4, чтобы получить 24 9.
0007Узнав коэффициент, на который нужно умножить знаменатель, умножьте и числитель, и знаменатель на одно и то же число, т.е. 4 x 4 ÷ 6 x 4 = 16 ÷ 24 и 5 x 3 ÷ 8 x 3 = 15 ÷ 24
Теперь у вас есть похожие дроби, то есть 16 ÷ 24 и 15 ÷ 24
0007Смешанная дробь, как следует из названия, состоит из целого, части и его объединенное целое. Он состоит из двух частей: целого числа и дроби. Смешанная дробь получается из неправильной дроби при ее делении. Частное, полученное после деления, образует целое число, остаток образует числитель оставшейся дроби, а делитель образует знаменатель.
Вот пример:
Если мы рассмотрим неправильную дробь 85 и разделим числитель на знаменатель путем деления в большую сторону, мы получим:Делитель = 5
Частное = 1
Остаток = 3
Чтобы преобразовать это в смешанной дроби частное становится целым, остаток становится числителем, а делитель становится знаменателем, то есть 1 x 3 ÷ 5 .
Эквивалентные дроби – это те дроби, которые имеют одинаковую приведенную форму, т.е. при приведении к простейшим формам эти дроби эквивалентны. Например, при приведении двух дробей 3 ÷ 6 и 2 ÷ 4 к их простейшему виду они будут равны 1 ÷ 2 и, следовательно, образуют пару эквивалентных дробей.
Аналогично пара дробей 9 ÷ 9 и 4 ÷ 4 будет равна 1 ÷ 1 при приведении к простейшему виду, т.е. образует пару равнозначных дробей.
Как выполнять операции с дробями
Выполнение математических операций с дробями может показаться запутанным или сложным, но если вы помните определенные эмпирические правила приближения к операциям с дробями, вы можете легко их выполнять. Здесь мы разбили для вас процесс решения математических операций с дробями на простые шаги.
- Сложение и вычитание
Самый первый и главный фактор, о котором следует помнить, это то, что всякий раз, когда вы выполняете сложение или вычитание пары дробей, они должны быть подобны дробям.
Следовательно, если пара дробей, которые вы добавляете/вычитаете, представляет собой пару одинаковых дробей, вы можете напрямую добавлять или вычитать их. Но в случае, если они не похожи на дроби, вы должны сначала преобразовать их в подобные дроби, как указано выше. - Умножение и деление
Для таких операций, как умножение и деление, вы можете напрямую выполнять вычисления с непохожей парой дробей.
Умножение дробей очень просто: сначала нужно перемножить числовые значения числителей и знаменателей. Потом просто полученный ответ в сокращенной форме.
Следовательно, если пара дробей, которые вы добавляете/вычитаете, представляет собой пару одинаковых дробей, вы можете напрямую добавлять или вычитать их. Но в случае, если они не похожи на дроби, вы должны сначала преобразовать их в подобные дроби, как указано выше.Преобразование обычных инженерных дробей в десятичные числа
В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже. (Необходимо изменить описание)
| 64-й | 32-й | 16-й | 34-й | 2-й | Десятичный | Десятичный (дюймы в мм) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1/64 | 0,015625 | 0,396875 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1/16 | 0,03125 | 0,79375 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3/64 | 0,0460875 | 2 1 33 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4/64 | 2/32 | 0,0625 | 1,5875 | 9 | 9 5/64 | 0,078125 | 1,984375 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6/64 | 60 3/32 9016 3/32 9016 1660,09375 | 2,38125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7/64 | 0,109375 | 2,778125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2/16 | 1/8 | 0,125 | 3,175 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9/64 | 0,140625 | 3,571875 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10/64 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 9 0166 | 0,15625 | 3,96875 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11/64 | 0. 171875 | 4.365625 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12/64 | 90/1333×90/1333×90 6/640 | 0 3/16 | 0,1875 | 4,7625 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13/64 | 0,203125 | 5,159375 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14/64 | 7/32 | 6 | 6 | 6 0,21875 | 5,55625 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15/64 | 0,234375 | 5,953125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16/64 | 8/32 | 3 13 9018 9018 3 | 1/4 | 1/4 | 0,25 | 6,35 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17/64 | 0,265625 | 6,746875 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18/64 6/6 132130 | 0 | 0,28125 | 7,14375 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19/64 | 0,296875 | 7,540625 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20/64 | 10/32 | 6 60 1/336 900 01660,3125 | 7,9375 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21/64 | 0,328125 | 8. 334375 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22/64 | 11/32 | 0,34375 | 60 8,73130 2|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23/64 | 0.359375 | 9.128125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24/64 | 12/32 | 6/16 | 3/8 9011 25 | 9,525 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25/64 | 0,3 | 9,5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26/64 | 13/32 | 0,40625 | 5 11 62 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27/64 | 0,421875 | 10,715625 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28/64 | 14/32 | 7/16 | 5,102 10137 | 555||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29/64 | 0,453125 | 11,509375 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30/64 | 15/32 | 0,46875 | 11, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31/34 31/34 | 0,484375 | 12,303125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32/64 | 16/32 | 8/16 | 4/8 | 2/4 | 2/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33/64 | 0,515625 | 13,096875 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34/64 | 17/32 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35/64 | 0,546875 | 13,8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36/64 | 18/32 | 9/16 | 0,5625 | 3 3| 0,578125 | 14,684375 | 38/ 64 | 9/32 | 0,59375 | 15,08125 | 39/64 | 6 | 0,609375 | 15,478125 | 40/64 | 20/32 | 10/16 | 5/8 | 0,625 | 15,875 | 3 112494 900 0133 0,640625 | 16,271875 | 42 /64 | 21/32 | 0,65625 | 16,66875 | 43/64 9016 66 | 0,671875 | 17,065625 | 44/64 | 22/32 | 16/11 | 0,6875 | 17,4625 | 9016 3 9016 3 64 9016 66 | 0,703125 | 17,859375 | 46/64 | 23/32 | 0,71875 | 18,25625 | 47/64 | 6 9,13060 9,1306 33 | 18. |  653125 48/64 | 24/32 | 12/16 | 6/8 | 3/6 | 3/6 | 0,75 | 19,05 | 0,765625 | 19,446875 | 50/ 64 | 25/32 | 0,78125 | 19,84375 | 51/64 9016 9016 66 | 0,796875 | 20,240625 | 52/64 | 26/32 | 13/16 | 0,8125 | 20,6375 | 53/64 | 9016 30 0,828125 | 21,034375 | 54/64 | 27/32 | 0,84375 | 21,43125 | 55/64 | 0,859375 | 56/64 | 28/32 | 14/16 | 7/8 | 0,875 | 22,225 | 57/64 | 8 11166 90,3 5 | 22,621875 | 58/64 | 29/32 | 0, | 23. |  01875 59/64 | 0, | 5 23,4115325 900 0130 60/64 | 30/32 | 15/16 | 0,9375 | 23,8125 | 61/64 | 9 0,9531339 2,9531325 375 62/64 | 31/32 | 0,96875 | 24,606259 | 63/64 | 0,984375 | 25,003125 | 64/64 | 311/320 321320 0 16/16 | 8/8 | 4/4 | 2/2 | 1 | 25.4 | |
Часто задаваемые вопросы о Калькуляторе дробей
Вычислять дроби очень просто: для сложения и вычитания преобразуйте дроби в одну и ту же пару, а затем выполняйте их. Для умножения или деления вы можете напрямую выполнять вычисления с дробями.
3/4 разделить на 2 будет равно 3/8.
½ от ¾ равно ⅜.
¼ x ¼, так как дробь будет ⅛
Вы можете разделить дроби, сначала инвертировав дробь делителя и умножив на нее дробь делимого.
Ответ следует привести к простейшей форме. Например:
Чтобы сравнить дроби, сначала преобразуйте их в подобные дроби. После этого сравните числители одинаковых дробей и больше та, у которой числитель больше. В отличие от дробей нельзя сравнивать напрямую.
Чтобы сложить дроби с разными знаменателями, сначала преобразуйте дроби в подобные дроби, чтобы получить одинаковый знаменатель (который будет НОК двух знаменателей). После этого сложите числители и приведите полученный ответ к простейшему виду.
Смешанная дробь — это дробная фигура, состоящая из двух частей: целого числа и дроби.
Нет, смешанные дроби можно получить только из неправильных дробей, так как их знаменатели меньше числителей, а значит, при длинном делении получится положительный остаток. С другой стороны, для правильных дробей длинное деление либо не даст остатка (делимое меньше делителя), либо даст нулевой остаток. Поэтому правильные дроби не могут образовывать смешанные дроби.
Чтобы сложить/вычесть две смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем выполните действия, аналогичные другим дробям.
| Бесплатные онлайн калькуляторы 0130 Конвертер INR в USD | |||
| Калькулятор рентабельности инвестиций (ROI) | Калькулятор дробей | ||
| Калькулятор галлонов в литр | Калькулятор метров и футов | ||
| Калькулятор возраста | |||
Калькулятор дробей — множитель дробей, сложение
0 Дробь Фракция? Части и значение
Дробь в самом простом значении этого слова относится к количеству, которое не является целым, таким образом выражая отношение часть-целое. С точки зрения математики дробь представляет собой количество частей целого. Итак, если мы представим 7 частей целого, состоящего из 10 частей, то дробь будет представлена как 7 ÷ 10.
Дробь представлена в виде части и целого, разделенных чертой деления. Математическая дробь также состоит из 2 частей:
- Числитель: появляется над линией деления и представляет часть.
- Знаменатель: появляется под чертой деления и представляет собой целое, частью которого является числитель.
Например, в дроби 2 ÷ 7 2 — числитель, а 7 — знаменатель.
Типы дробей
В математике дроби могут быть 6 основных типов, в которых категории не являются исключительными (т. е. конкретная дробь может попадать более чем в одну категорию).
- Правильная дробь
Правильная дробь – это дробь, у которой числитель меньше знаменателя. Так, 8 ÷ 17, 2 ÷ 5, 1 ÷ 5 и т. д. — все это примеры правильных дробей в качестве их числителей, т. е. числа над чертой деления (8, 2, 1) меньше знаменателей, т. е. числа, выраженные ниже линия разделения (17, 5, 5).
- Неправильная дробь
Неправильной дробью называется дробь, в которой знаменатель меньше числителя (и наоборот, числитель больше знаменателя). Так, например, примеры неправильных дробей включают 8 ÷ 5, 4 ÷ 3, 3 ÷ 2.
- Одинаковые дроби
Одинаковые дроби состоят из пары дробей с одинаковым знаменателем.
Такие операции, как сложение и вычитание, можно выполнять непосредственно над одинаковыми дробями. Так, например, 49а 79 похожи на дроби. Точно так же 3 ÷ 5 и 2 ÷ 5 также похожи на дроби - В отличие от дробей
В отличие от дробей относятся к паре дробей, в которых знаменатели различны. Чтобы выполнять такие действия, как сложение и вычитание над неправильными дробями, их нужно сначала преобразовать в одинаковые дроби. Например, 4 ÷ 9 и 5 ÷ 8 являются парой непохожих дробей, так как их знаменатели (9 и 8) различны и не равны.
Во многих математических операциях вам может понадобиться преобразовать неправильную дробь в правильную дробь. Вот как это сделать:
Такие операции, как сложение и вычитание, можно выполнять непосредственно над одинаковыми дробями. Так, например, 49а 79 похожи на дроби. Точно так же 3 ÷ 5 и 2 ÷ 5 также похожи на дробиСначала найдите наименьшее общее кратное (НОК) дробей. Например, для 4 ÷ 6 и 5 ÷ 8 знаменатели равны 6 и 8, а НОК 6 и 8 равен 24.
вам придется умножить знаменатели, чтобы получить LCM. (Легкий трюк — разделить НОК на знаменатель). Например, в случае числа 8 его нужно умножить на 3, чтобы получить 24, а в случае 6 его нужно умножить на 4, чтобы получить 24 9.
0007Узнав коэффициент, на который нужно умножить знаменатель, умножьте и числитель, и знаменатель на одно и то же число, т.е. 4 x 4 ÷ 6 x 4 = 16 ÷ 24 и 5 x 3 ÷ 8 x 3 = 15 ÷ 24
Теперь у вас есть похожие дроби, то есть 16 ÷ 24 и 15 ÷ 24
0007Смешанная дробь, как следует из названия, состоит из целого, части и его объединенное целое. Он состоит из двух частей: целого числа и дроби. Смешанная дробь получается из неправильной дроби при ее делении. Частное, полученное после деления, образует целое число, остаток образует числитель оставшейся дроби, а делитель образует знаменатель.
Вот пример:
Если мы рассмотрим неправильную дробь 85 и разделим числитель на знаменатель путем деления в большую сторону, мы получим:Делитель = 5
Частное = 1
Остаток = 3
Чтобы преобразовать это в смешанной дроби частное становится целым, остаток становится числителем, а делитель становится знаменателем, то есть 1 x 3 ÷ 5 .
Эквивалентные дроби – это те дроби, которые имеют одинаковую приведенную форму, т.е. при приведении к простейшим формам эти дроби эквивалентны. Например, при приведении двух дробей 3 ÷ 6 и 2 ÷ 4 к их простейшему виду они будут равны 1 ÷ 2 и, следовательно, образуют пару эквивалентных дробей.
Аналогично пара дробей 9 ÷ 9 и 4 ÷ 4 будет равна 1 ÷ 1 при приведении к простейшему виду, т.е. образует пару равнозначных дробей.
Как выполнять операции с дробями
Выполнение математических операций с дробями может показаться запутанным или сложным, но если вы помните определенные эмпирические правила приближения к операциям с дробями, вы можете легко их выполнять. Здесь мы разбили для вас процесс решения математических операций с дробями на простые шаги.
- Сложение и вычитание
Самый первый и главный фактор, о котором следует помнить, это то, что всякий раз, когда вы выполняете сложение или вычитание пары дробей, они должны быть подобны дробям.
Следовательно, если пара дробей, которые вы добавляете/вычитаете, представляет собой пару одинаковых дробей, вы можете напрямую добавлять или вычитать их. Но в случае, если они не похожи на дроби, вы должны сначала преобразовать их в подобные дроби, как указано выше. - Умножение и деление
Для таких операций, как умножение и деление, вы можете напрямую выполнять вычисления с непохожей парой дробей.
Умножение дробей очень просто: сначала нужно перемножить числовые значения числителей и знаменателей. Потом просто полученный ответ в сокращенной форме.
Следовательно, если пара дробей, которые вы добавляете/вычитаете, представляет собой пару одинаковых дробей, вы можете напрямую добавлять или вычитать их. Но в случае, если они не похожи на дроби, вы должны сначала преобразовать их в подобные дроби, как указано выше.Преобразование обычных инженерных дробей в десятичные числа
В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже. (Необходимо изменить описание)
| 64-й | 32-й | 16-й | 34-й | 2-й | Десятичный | Десятичный (дюймы в мм) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1/64 | 0,015625 | 0,396875 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1/16 | 0,03125 | 0,79375 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3/64 | 0,0460875 | 2 1 33 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4/64 | 2/32 | 0,0625 | 1,5875 | 9 | 9 5/64 | 0,078125 | 1,984375 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6/64 | 60 3/32 9016 3/32 9016 1660,09375 | 2,38125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7/64 | 0,109375 | 2,778125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2/16 | 1/8 | 0,125 | 3,175 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9/64 | 0,140625 | 3,571875 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10/64 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 9 0166 | 0,15625 | 3,96875 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11/64 | 0. 171875 | 4.365625 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12/64 | 90/1333×90/1333×90 6/640 | 0 3/16 | 0,1875 | 4,7625 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13/64 | 0,203125 | 5,159375 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14/64 | 7/32 | 6 | 6 | 6 0,21875 | 5,55625 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15/64 | 0,234375 | 5,953125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16/64 | 8/32 | 3 13 9018 9018 3 | 1/4 | 1/4 | 0,25 | 6,35 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17/64 | 0,265625 | 6,746875 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18/64 6/6 132130 | 0 | 0,28125 | 7,14375 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19/64 | 0,296875 | 7,540625 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20/64 | 10/32 | 6 60 1/336 900 01660,3125 | 7,9375 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21/64 | 0,328125 | 8. 334375 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22/64 | 11/32 | 0,34375 | 60 8,73130 2|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23/64 | 0.359375 | 9.128125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24/64 | 12/32 | 6/16 | 3/8 9011 25 | 9,525 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25/64 | 0,3 | 9,5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26/64 | 13/32 | 0,40625 | 5 11 62 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27/64 | 0,421875 | 10,715625 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28/64 | 14/32 | 7/16 | 5,102 10137 | 555||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29/64 | 0,453125 | 11,509375 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30/64 | 15/32 | 0,46875 | 11, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31/34 31/34 | 0,484375 | 12,303125 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32/64 | 16/32 | 8/16 | 4/8 | 2/4 | 2/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33/64 | 0,515625 | 13,096875 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34/64 | 17/32 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35/64 | 0,546875 | 13,8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36/64 | 18/32 | 9/16 | 0,5625 | 3 3| 0,578125 | 14,684375 | 38/ 64 | 9/32 | 0,59375 | 15,08125 | 39/64 | 6 | 0,609375 | 15,478125 | 40/64 | 20/32 | 10/16 | 5/8 | 0,625 | 15,875 | 3 112494 900 0133 0,640625 | 16,271875 | 42 /64 | 21/32 | 0,65625 | 16,66875 | 43/64 9016 66 | 0,671875 | 17,065625 | 44/64 | 22/32 | 16/11 | 0,6875 | 17,4625 | 9016 3 9016 3 64 9016 66 | 0,703125 | 17,859375 | 46/64 | 23/32 | 0,71875 | 18,25625 | 47/64 | 6 9,13060 9,1306 33 | 18. |  653125 48/64 | 24/32 | 12/16 | 6/8 | 3/6 | 3/6 | 0,75 | 19,05 | 0,765625 | 19,446875 | 50/ 64 | 25/32 | 0,78125 | 19,84375 | 51/64 9016 9016 66 | 0,796875 | 20,240625 | 52/64 | 26/32 | 13/16 | 0,8125 | 20,6375 | 53/64 | 9016 30 0,828125 | 21,034375 | 54/64 | 27/32 | 0,84375 | 21,43125 | 55/64 | 0,859375 | 56/64 | 28/32 | 14/16 | 7/8 | 0,875 | 22,225 | 57/64 | 8 11166 90,3 5 | 22,621875 | 58/64 | 29/32 | 0, | 23. |  01875 59/64 | 0, | 5 23,4115325 900 0130 60/64 | 30/32 | 15/16 | 0,9375 | 23,8125 | 61/64 | 9 0,9531339 2,9531325 375 62/64 | 31/32 | 0,96875 | 24,606259 | 63/64 | 0,984375 | 25,003125 | 64/64 | 311/320 321320 0 16/16 | 8/8 | 4/4 | 2/2 | 1 | 25.4 | |
Часто задаваемые вопросы о Калькуляторе дробей
Вычислять дроби очень просто: для сложения и вычитания преобразуйте дроби в одну и ту же пару, а затем выполняйте их. Для умножения или деления вы можете напрямую выполнять вычисления с дробями.
3/4 разделить на 2 будет равно 3/8.
½ от ¾ равно ⅜.
¼ x ¼, так как дробь будет ⅛
Вы можете разделить дроби, сначала инвертировав дробь делителя и умножив на нее дробь делимого.
Чтобы сравнить дроби, сначала преобразуйте их в подобные дроби. После этого сравните числители одинаковых дробей и больше та, у которой числитель больше. В отличие от дробей нельзя сравнивать напрямую.
Чтобы сложить дроби с разными знаменателями, сначала преобразуйте дроби в подобные дроби, чтобы получить одинаковый знаменатель (который будет НОК двух знаменателей). После этого сложите числители и приведите полученный ответ к простейшему виду.
Смешанная дробь — это дробная фигура, состоящая из двух частей: целого числа и дроби.
Нет, смешанные дроби можно получить только из неправильных дробей, так как их знаменатели меньше числителей, а значит, при длинном делении получится положительный остаток. С другой стороны, для правильных дробей длинное деление либо не даст остатка (делимое меньше делителя), либо даст нулевой остаток. Поэтому правильные дроби не могут образовывать смешанные дроби.
Чтобы сложить/вычесть две смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем выполните действия, аналогичные другим дробям.