Вычитание и сложение корней: Сложение и вычитание квадратных корней: определение, примеры, правила

Квадратный корень. Действия с квадратными корнями. Модуль. Сравнение квадратных корней

Факт 1.
\(\bullet\) Возьмем некоторое неотрицательное число \(a\) (то есть \(a\geqslant 0\)). Тогда (арифметическим) квадратным корнем из числа \(a\) называется такое неотрицательное число \(b\), при возведении которого в квадрат мы получим число \(a\): \[\sqrt a=b\quad \text{то же самое, что }\quad a=b^2\] Из определения следует, что \(a\geqslant 0, b\geqslant 0\). Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть \(100^2=10000\geqslant 0\) и \((-100)^2=10000\geqslant 0\).
\(\bullet\) Чему равен \(\sqrt{25}\)? Мы знаем, что \(5^2=25\) и \((-5)^2=25\). Так как по определению мы должны найти неотрицательное число, то \(-5\) не подходит, следовательно, \(\sqrt{25}=5\) (так как \(25=5^2\)).
Нахождение значения \(\sqrt a\) называется извлечением квадратного корня из числа \(a\), а число \(a\) называется подкоренным выражением.
\(\bullet\) Исходя из определения, выражения \(\sqrt{-25}\), \(\sqrt{-4}\) и т.п. не имеют смысла.

Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от \(1\) до \(20\): \[\begin{array}{|ll|} \hline 1^2=1 & \quad11^2=121 \\ 2^2=4 & \quad12^2=144\\ 3^2=9 & \quad13^2=169\\ 4^2=16 & \quad14^2=196\\ 5^2=25 & \quad15^2=225\\ 6^2=36 & \quad16^2=256\\ 7^2=49 & \quad17^2=289\\ 8^2=64 & \quad18^2=324\\ 9^2=81 & \quad19^2=361\\ 10^2=100& \quad20^2=400\\ \hline \end{array}\]

Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\] Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\), то первоначально вы должны найти значения \(\sqrt{25}\) и \(\sqrt{49}\), а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\) или \(\sqrt b\) при сложении \(\sqrt a+\sqrt b\) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt 2+ \sqrt {49}\) мы можем найти \(\sqrt{49}\) – это \(7\), а вот \(\sqrt 2\) никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt 2+7\). Дальше это выражение, к сожалению, упростить никак нельзя \(\bullet\) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad \sqrt a:\sqrt b=\sqrt{a:b}\] (

при условии, что обе части равенств имеют смысл)
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot 2}=\sqrt{64}=8\); \(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\); \(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}= 5\cdot 8=40\). \(\bullet\) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\). Так как \(44100:100=441\), то \(44100=100\cdot 441\). По признаку делимости число \(441\) делится на \(9\) (так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\), то есть \(441=9\cdot 49\).
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}= \sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}= \sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{ \dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot \sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]

\(\bullet\) Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\) (сокращенная запись от выражения \(5\cdot \sqrt2\)). Так как \(5=\sqrt{25}\), то \[5\sqrt2=\sqrt{25}\cdot \sqrt2=\sqrt{25\cdot 2}=\sqrt{50}\] Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\),
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\).

Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число \(\sqrt2\) мы не можем. Представим, что \(\sqrt2\) – это некоторое число \(a\). Соответственно, выражение \(\sqrt2+3\sqrt2\) есть не что иное, как \(a+3a\) (одно число \(a\) плюс еще три таких же числа \(a\)). А мы знаем, что это равно четырем таким числам \(a\), то есть \(4\sqrt2\).

Факт 4.
\(\bullet\) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака \(\sqrt {} \ \) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа \(16\) можно, потому что \(16=4^2\), поэтому \(\sqrt{16}=4\). А вот извлечь корень из числа \(3\), то есть найти \(\sqrt3\), нельзя, потому что нет такого числа, которое в квадрате даст \(3\).

Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\) и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\)), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\)) и т.д.
\(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.

Факт 5.
\(\bullet\) Модуль вещественного числа \(a\) – это неотрицательное число \(|a|\), равное расстоянию от точки \(a\) до \(0\) на вещественной прямой. Например, \(|3|\) и \(|-3|\) равны 3, так как расстояния от точек \(3\) и \(-3\) до \(0\) одинаковы и равны \(3\).
\(\bullet\) Если \(a\) – неотрицательное число, то \(|a|=a\).
Пример: \(|5|=5\); \(\qquad |\sqrt2|=\sqrt2\). \(\bullet\) Если \(a\) – отрицательное число, то \(|a|=-a\).
Пример: \(|-5|=-(-5)=5\); \(\qquad |-\sqrt3|=-(-\sqrt3)=\sqrt3\).
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число \(0\), модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная \(x\) (или какая-то другая неизвестная), например, \(|x|\), про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: \(|x|\). \(\bullet\) Имеют место следующие формулы: \[{\large{\sqrt{a^2}=|a|}}\] \[{\large{(\sqrt{a})^2=a}}, \text{ при условии } a\geqslant 0\] Очень часто допускается такая ошибка: говорят, что \(\sqrt{a^2}\) и \((\sqrt a)^2\) – одно и то же. Это верно только в том случае, когда \(a\) – положительное число или ноль. А вот если \(a\) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо \(a\) число \(-1\). Тогда \(\sqrt{(-1)^2}=\sqrt{1}=1\), а вот выражение \((\sqrt {-1})^2\) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).
Поэтому обращаем ваше внимание на то, что \(\sqrt{a^2}\) не равен \((\sqrt a)^2\)! Пример: 1) \(\sqrt{\left(-\sqrt2\right)^2}=|-\sqrt2|=\sqrt2\), т.к. \(-\sqrt2<0\);

\(\phantom{00000}\) 2) \((\sqrt{2})^2=2\). \(\bullet\) Так как \(\sqrt{a^2}=|a|\), то \[\sqrt{a^{2n}}=|a^n|\] (выражение \(2n\) обозначает четное число)
То есть при извлечении корня из числа, находящегося в какой-то степени, эта степень уменьшается в два раза.
Пример:
1) \(\sqrt{4^6}=|4^3|=4^3=64\)
2) \(\sqrt{(-25)^2}=|-25|=25\) (заметим, что если модуль не поставить, то получится, что корень из числа равен \(-25\); но мы помним, что по определению корня такого быть не может: у нас всегда при извлечении корня должно получаться положительное число или ноль)
3) \(\sqrt{x^{16}}=|x^8|=x^8\) (так как любое число в четной степени неотрицательно)

Факт 6.
Как сравнить два квадратных корня?
\(\bullet\) Для квадратных корней верно: если \(\sqrt a<\sqrt b\), то \(a<b\); если \(\sqrt a=\sqrt b\), то \(a=b\).
Пример:
1) сравним \(\sqrt{50}\) и \(6\sqrt2\). Для начала преобразуем второе выражение в \(\sqrt{36}\cdot \sqrt2=\sqrt{36\cdot 2}=\sqrt{72}\). Таким образом, так как \(50<72\), то и \(\sqrt{50}<\sqrt{72}\). Следовательно, \(\sqrt{50}<6\sqrt2\).
2) Между какими целыми числами находится \(\sqrt{50}\)?
Так как \(\sqrt{49}=7\), \(\sqrt{64}=8\), а \(49<50<64\), то \(7<\sqrt{50}<8\), то есть число \(\sqrt{50}\) находится между числами \(7\) и \(8\).
3) Сравним \(\sqrt 2-1\) и \(0,5\). Предположим, что \(\sqrt2-1>0,5\): \[\begin{aligned} &\sqrt 2-1>0,5 \ \big| +1\quad \text{(прибавим единицу к обеим частям)}\\[1ex] &\sqrt2>0,5+1 \ \big| \ ^2 \quad\text{(возведем обе части в квадрат)}\\[1ex] &2>1,5^2\\ &2>2,25 \end{aligned}\] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1<0,5\).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3<\sqrt2\) нельзя (убедитесь в этом сами)! \(\bullet\) Следует запомнить, что \[\begin{aligned} &\sqrt 2\approx 1,4\\[1ex] &\sqrt 3\approx 1,7 \end{aligned}\] Знание приблизительного значения данных чисел поможет вам при сравнении чисел! \(\bullet\) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. Покажем, как это работает, на примере.
Возьмем \(\sqrt{28224}\). Мы знаем, что \(100^2=10\,000\), \(200^2=40\,000\) и т.д. Заметим, что \(28224\) находится между \(10\,000\) и \(40\,000\). Следовательно, \(\sqrt{28224}\) находится между \(100\) и \(200\).
Теперь определим, между какими “десятками” находится наше число (то есть, например, между \(120\) и \(130\)). Также из таблицы квадратов знаем, что \(11^2=121\), \(12^2=144\) и т.д., тогда \(110^2=12100\), \(120^2=14400\), \(130^2=16900\), \(140^2=19600\), \(150^2=22500\), \(160^2=25600\), \(170^2=28900\). Таким образом, мы видим, что \(28224\) находится между \(160^2\) и \(170^2\). Следовательно, число \(\sqrt{28224}\) находится между \(160\) и \(170\).
Попробуем определить последнюю цифру. Давайте вспомним, какие однозначные числа при возведении в квадрат дают на конце \(4\)? Это \(2^2\) и \(8^2\). Следовательно, \(\sqrt{28224}\) будет заканчиваться либо на 2, либо на 8. Проверим это. Найдем \(162^2\) и \(168^2\):
\(162^2=162\cdot 162=26224\)
\(168^2=168\cdot 168=28224\).
Следовательно, \(\sqrt{28224}=168\). Вуаля!

Содержание

Как складывать и вычитать квадратные корни

Сейчас в школьной программе происходит, что-то не совсем понятно. Одно радует, что в математике все остается неизменной. Работа с корнями, а именно складывание и вычитание не очень сложное действие. Но у некоторых учеников вызывают определенные трудности.

И в этой статье мы разберем правила, как складывать и вычитать квадратные корни.

Вычитать и складывать квадратные корни можно если срабатывает условие, что у этих корней имеются одинаковые подкоренные выражения. Другими словами, мы можем проводить действия с 2√3 и 4√3, а не с 2√3 и 2√7. Но можно провести действия по упрощению подкоренного выражения, чтобы потом привести их к корням, которые будут иметь одинаковые подкоренные выражения. И только после этого уже начать складывать или вычитать.

Теория складывания и вычитания квадратных корней

Сам принцип очень простой. И составит из трех действий. Нужно упростить подкоренной выражение. Найти получившиеся одинаковые подкоренные выражения и сложить или вычесть корни.

Как упростить подкоренное выражение

Для этого нужно разложить подкоренное число, что бы состояло из двух множителей. Главное условие. Одно из этих чисел должно быть квадратным числом (пример: 25 или 9). После этого действия мы извлекаем корень из данного квадратного числа. И записываем это число перед нашим корнем, а под корнем у нас остается второй множитель.

Например, 6√50 — 2√8 + 5√12

6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Тут мы раскладываем 50 на два множителя 25 и 2. Потом из 25 мы извлекаем квадратный корень (получаем число 5) и выносим его из под корня. Далее 5 умножаем на 6 и получаем 30√2

2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. В данном примеры мы 8 раскладываем на два числа 4 и 2. Из 4 извлекаем корень и выносим получившееся число за корень и умножаем его на то число которое было уже за корнем.

5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Тут мы, как и раньше число под корнем раскладываем на два числа 4 и 3. Из 4-х извлекаем корень. Получившееся число выносим за корень и перемножаем его на то число которое было за корнем.

В итоге мы преобразовали уравнение 6√50 — 2√8 + 5√12 в такой вид 30√2 — 4√2 + 10√3

Подчеркиваем корни у которых одинаковы подкоренные выражения

В нашем примере 30√2 — 4√2 + 10√3 мы выделяем 30√2 и 4√2 Так, как у этих чисел одинаковое подкоренное число 2.
Если в Вашем примере несколько одинаковых подкоренных выражений. Подчеркивайте одинаковые из них разными линиями.

Складываем или вычитаем наши корни

Теперь складываем или вычитаем числа которые имеют одинаковые подкоренные выражения. А то, что под корнем мы оставляем неизменным. Смысл в том, чтобы показать сколько всего корней с определенными подкоренными выражениями есть в заданном уравнении.

В нашем примере 30√2 — 4√2 + 10√3 мы от 30 отнимаем 4 и получаем 26√2

Ответ в нашем примере будет такой. 26√2 + 10√3

Sabibon — самое интересное в интернете

Как складывать квадратные корни

Квадратным корнем из числа X называется число A, которое в процессе умножения самого на себя (A * A) может дать число X.
Т.е. A * A = A² = X, и √X = A.

Над квадратными корнями (√x), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.

Шаг 1. Извлечение квадратных корней

Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9. Первое число 4 является квадратом числа 2. Второе число 9 является квадратом числа 3. Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5.
Все, пример решен. Но так просто бывает далеко не всегда.

Шаг 2. Вынесение множителя числа из-под корня

Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54.

Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3,
54 = 2 * 3 * 3 * 3

В числе 24 мы имеем множитель 4, его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9.

Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6.

Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.

Шаг 3. Сокращение знаменателя

Рассмотрим следующую ситуацию: сумма двух квадратных корней – это знаменатель дроби, например, A / (√a + √b).
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b.

Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a – b.

Аналогично, если в знаменателе имеется разность корней: √a — √b

, числитель и знаменатель дроби умножаем на выражение √a + √b.

Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ( (√3 + √5) * (√3 — √5) ) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3).

Пример сложного сокращения знаменателя

Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.

Для примера берём дробь: 12 / (√2 + √3 + √5).
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5.

Получаем:

12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.

Шаг 4. Вычисление приблизительного значения на калькуляторе

Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.

Пример вычисления приблизительного значения

Необходимо вычислить приблизительное значение данного выражения √7 + √5.

В итоге получаем:

√7 + √5 ≈ 2,65 + 2,24 = 4,89.

Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.

Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.

Сложение и вычитание корней правила. Как складывать квадратные корни

Извлечение квадрантного корня из числа не единственная операция, которую можно производить с этим математическим явлением. Так же как и обычные числа, квадратные корни складывают и вычитают.

Yandex.RTB R-A-339285-1

Правила сложения и вычитания квадратных корней

Определение 1

Такие действия, как сложение и вычитание квадратного корня, возможны только при условии одинакового подкоренного выражения.

Пример 1

Можно сложить или вычесть выражения 2 3 и 6 3 , но не 5 6 и 9 4 . Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.

Действия с корнями: основы

Пример 2

6 50 — 2 8 + 5 12

Алгоритм действия:

Упростить подкоренное выражение . Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня. Обращаем ваше внимание, что второй множитель заносится под знак корня.

После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!

Совет 1

Если у вас пример с большим количеством одинаковых подкоренных выражений, то подчеркивайте такие выражения одинарными, двойными и тройными линиями, чтобы облегчить процесс вычисления.

Пример 3

Давайте попробуем решить данный пример:

6 50 = 6 (25 × 2) = (6 × 5) 2 = 30 2 . Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .

2 8 = 2 (4 × 2) = (2 × 2) 2 = 4 2 . Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 4 2 .

5 12 = 5 (4 × 3) = (5 × 2) 3 = 10 3 . Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .

Результат упрощения: 30 2 — 4 2 + 10 3

30 2 — 4 2 + 10 3 = (30 — 4) 2 + 10 3 = 26 2 + 10 3 .

В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.

Пример 4

Упрощаем (45) . Раскладываем 45 на множители: (45) = (9 × 5) ;
Выносим 3 из-под корня (9 = 3) : 45 = 3 5 ;
Складываем множители у корней: 3 5 + 4 5 = 7 5 .

Пример 5

6 40 — 3 10 + 5:

Упрощаем 6 40 . Раскладываем 40 на множители: 6 40 = 6 (4 × 10) ;

Выносим 2 из-под корня (4 = 2) : 6 40 = 6 (4 × 10) = (6 × 2) 10 ;
Перемножаем множители, которые стоят перед корнем: 12 10 ;
Записываем выражение в упрощенном виде: 12 10 — 3 10 + 5 ;
Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: (12 — 3) 10 = 9 10 + 5 .

Пример 6

Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.д.) и записываем результат:

(9 — 4) 5 — 2 3 = 5 5 — 2 3 .

Советы:

Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.
Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
Не следует суммировать или вычитать целое число или корень: 3 + (2 x) 1 / 2 .
При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число X .
Т.е. A * A = A 2 = X , и √X = A .

Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.

Шаг 1. Извлечение квадратных корней

сложение и вычитание. Как вычесть корень из числа

В математике любое действие имеет свою пару-противоположность – в сущности, это представляет собою одно из проявлений гегелевского закона диалектики: «единство и борьба противоположностей». Одно из действий в такой «паре» направлено на увеличение числа, а другое, обратное ему – на уменьшение. Например, действие, противоположное сложению – это вычитание, умножению соответствует деление. Имеется и своя диалектическая пара-противоположность и у возведения в степень. Речь идет об извлечении корня.

Извлечь из числа корень такой-то степени – это значит вычислить, какое число необходимо возвести в соответствующую степень, чтобы в итоге получилось данное число. Две степени имеют свои отдельные названия: вторая степень называется «квадратом», а третья – «кубом». Соответствено, корни данных степеней приятно именовать квадратным корнем и кубическим. Действия с кубическими корнями – тема для отдельного разговора, а сейчас поговорим о сложении квадратных корней.

Начнем с того, что в ряде случаев квадратные корни проще сначала извлечь, а потом уже складывать результаты. Предположим, нам необходимо найти значение такого выражения:

Ведь совсем не сложно вычислить, что корень квадратный из 16 равен 4, а из 121 – 11. Следовательно,

√16+√121=4+11=15

Впрочем, это самый простой случай – здесь речь идет о полных квадратах, т.е. о таких числах, которые получаются при возведении в квадрат целых чисел. Но так бывает не всегда. Например, число 24 – это не полный квадрат (не найти такого целого числа, которое при возведении его во вторую степень дало бы в результате 24). То же самое относится к такому числу, как 54… Что делать, если нам необходимо сложить корни квадратные из этих чисел?

В таком случае мы получим в ответе не число, а другое выражение. Максимум, что мы можем тут сделать – это максимально упростить исходное выражение. Для этого придется вынести множители из-под корня квадратного. Посмотрим, как это делается, на примере упомянутым чисел:

Для начала разложим на множители 24 – таким образом, чтобы из одного из них легко можно было извлечь корень квадратный (т.е., чтобы он был полным квадратом). Такое числи есть – это 4:

Теперь проделаем то же самое с 54. В его состав

Как вычитать квадратные корни между собой. Правила сложения квадратных корней

Квадратным корнем из числа x называют число a, которое при умножении само на себя дает число x: a * a = a^2 = x, ?x = a. Как и над всякими числами, над квадратными корнями дозволено исполнять арифметические операции сложения и вычитания.

Инструкция

1. Во-первых, при сложении квадратных корней испробуйте извлечь эти корни. Это будет допустимо, если числа под знаком корня являются полными квадратами. Скажем, пускай задано выражение?4 + ?9. Первое число 4 – это квадрат числа 2. Второе число 9 – это квадрат числа 3. Таким образом получается, что: ?4 + ?9 = 2 + 3 = 5.

2. Если под знаком корня нет полных квадратов, то испробуйте перенести из под знака корня множитель числа. Скажем, пускай дано выражение?24 + ?54. Разложите числа на множители: 24 = 2 * 2 * 2 * 3, 54 = 2 * 3 * 3 * 3. В числе 24 имеется множитель 4, тот, что дозволено перенести из под знака квадратного корня. В числе 54 – множитель 9. Таким образом, получается что: ?24 + ?54 = ?(4 * 6) + ?(9 * 6) = 2 * ?6 + 3 * ?6 = 5 * ?6. В данном примере в итоге выноса множителя из под знака корня получилось упростить заданное выражение.

3. Пускай сумма 2-х квадратных корней является знаменателем дроби, скажем, A / (?a + ?b). И пускай перед вами стоит задача «избавиться от иррациональности в знаменателе». Тогда дозволено воспользоваться дальнейшим методом. Умножьте числитель и знаменатель дроби на выражение?a – ?b. Таким образом в знаменателе получится формула сокращенного умножения: (?a + ?b) * (?a – ?b) = a – b. По аналогии, если в знаменателе дана разность корней: ?a – ?b, то числитель и знаменатель дроби нужно умножить на выражение?a + ?b. Для примера, пускай дана дробь 4 / (?3 + ?5) = 4 * (?3 – ?5) / ((?3 + ?5) * (?3 – ?5)) = 4 * (?3 – ?5) / (-2) = 2 * (?5 – ?3).

4. Разглядите больше непростой пример избавления от иррациональности в знаменателе. Пускай дана дробь 12 / (?2 + ?3 + ?5). Нужно умножить числитель и знаменатель дроби на выражени

Калькулятор корней с решением онлайн

Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12), для ввода обыкновенных дробей воспользуйтесь знаком «/» (например, 1/2 или 3/4).

Корень в математике

Операция извлечения корня из числа, является обратной операцией к операции возведения в степень.

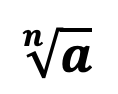
Обозначение: корень обозначается при помощи символа, который называется знаком корня. Число a, которое находится под корнем называется подкоренным выражением, а число n, расположенное слева от символа корня, называется – степенью корня.

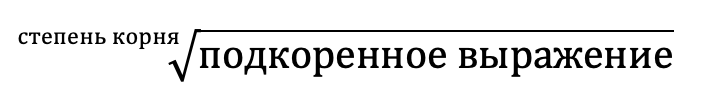
Степень корня – должна быть выражена натуральным числом (1, 2, 3, 4, 5…), т.е. не может быть отрицательной, нулем или дробным числом.

По сути, как уже было сказано выше извлечь корень из числа а означает возведение числа a в дробную степень, числителем которой выступает степень числа a, а знаменателем – степень корня.

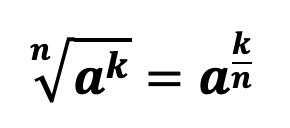
Следует заметить, что если степень корня равна 2, то число два как правило не пишут, а такой корень называется – квадратным.

Приведем примеры:

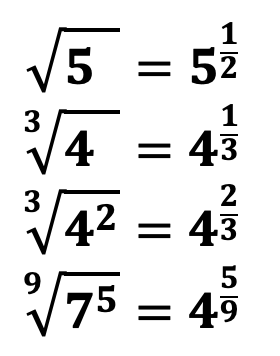
Извлечь корень из числа а означает возведение числа a в дробную степень

Приведем примеры извлечения корня:

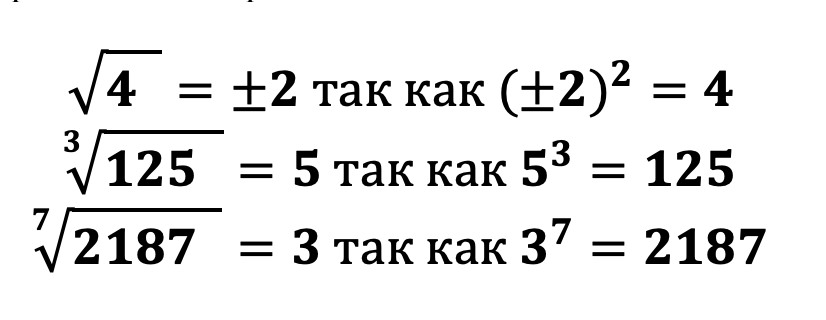
Исходя из вышенаписанных примеров можно сделать вывод, что когда мы хотим извлечь корень, к примеру 2-й степени, то нам необходимо найти такое число, что при возведении во 2-ю степень мы получим подкоренное выражение. То есть под корнем всегда находится число, уже возведенное в степень равную степени корня!

Четная и нечетная степень корня

Корень нечетной степени

При извлечении корня нечетной степени из положительного числа будем всегда получать положительное число, например:

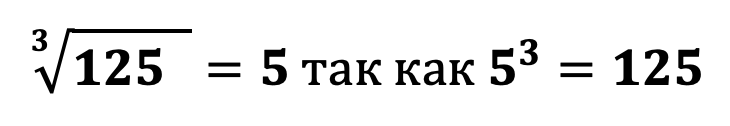
Извлечение корня нечетной степени из положительного числа

При извлечении корня нечетной степени из отрицательного числа будем всегда получать отрицательное число, например

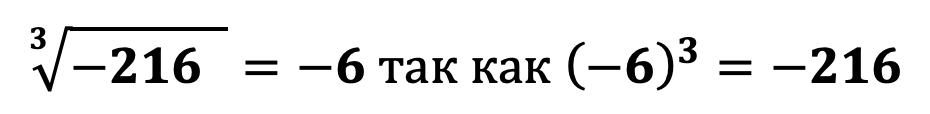
Извлечение корня нечетной степени из отрицательного числа

В данном примере можно легко увидеть почему при извлечении корня нечетной степени из отрицательного числа всегда будет получаться отрицательно число. Как известно чтобы возвести число в степень необходимо его умножить само на себя в количестве показателя степени : если (-6) умножить на (-6) получится положительное число 36 (мы знаем, что при умножении двух отрицательных чисел будет получаться положительное число), затем если умножить число 36 на (-6) получим -216, так как при умножении отрицательного числа на положительное всегда будет получаться отрицательное число.

Корень четной степени

При извлечении корня четной степени из положительного числа всегда будет получать два значения с противоположенными знаками. Это связанно с тем, что если представить, к примеру функцию квадратного корня y= √x и посмотреть на ее график, то мы увидим, что каждому значению xсоответствует два значения корня, одно положительное, а другое отрицательное.

Для понимания данного факта, нет необходимости строить график, рассмотрим на примере извлечение квадратного корня из числа 4:

Квадратный корень из 4 равен 2 так как = 4 и . Проверим 2 ⋅ 2 = 4 и -2 ⋅(-2) = 4.

Приведем еще пример с четной степенью корня для положительного числа.

Корень степени 4 за числа 81 равен 3 так как = 81 и . Проверим 3 ⋅ 3 ⋅ 3 ⋅ 3 = 81 и -3 ⋅ (-3) ⋅ (-3) ⋅ (-3) = 81

Теперь рассмотрим ситуацию, когда под корнем четной степени стоит отрицательное число.

Допустим, мы ходим извлечь квадратный корень из отрицательного числа, например, √-4 теперь подумаем есть ли вообще такое число, которое при возведении в квадрат давало бы -4? Ответ – нет! Любое число при возведении в четную степень всегда будет положительным. Поэтому корня чётной степени из любого отрицательного числа не существует в области вещественных чисел, поскольку при возведении любого вещественного числа в степень с чётным показателем результатом будет неотрицательное число.

Тем не менее извлечь корень четной степени всё-таки можно, но результатом будет всегда комплексное число, например:

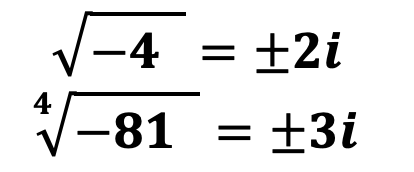
Под корнем четной степени стоит отрицательное число

Арифметический и алгебраический корни

Для упрощения записи корня четной степени из положительного числа, в калькуляторах, школьных учебниках и т.д. было введено понятие арифметического корня, значение которого, представляется всегда положительным числом. Алгебраический корень в свою очередь для корня четной степени из положительного числа является полным ответом и содержит как положительные, так и отрицательные значения.

Арифметический корень – упрощенная запись корня четной степени из положительного числа, всегда положительный. Например:

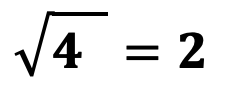
Алгебраический корень – полная запись корня четной степени из положительного числа. Например:

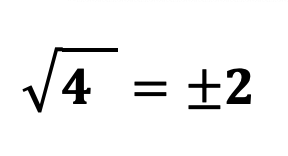
Как упростить корень

Для того, чтобы упростить любой корень, необходимо разложить подкоренное выражение на простые множители (для разложения числа на простые множители можно воспользоваться калькулятором разложения числа на простые множители) и вынести за знак корня тот множитель, который повторяется равное степени корня число раз. Например:

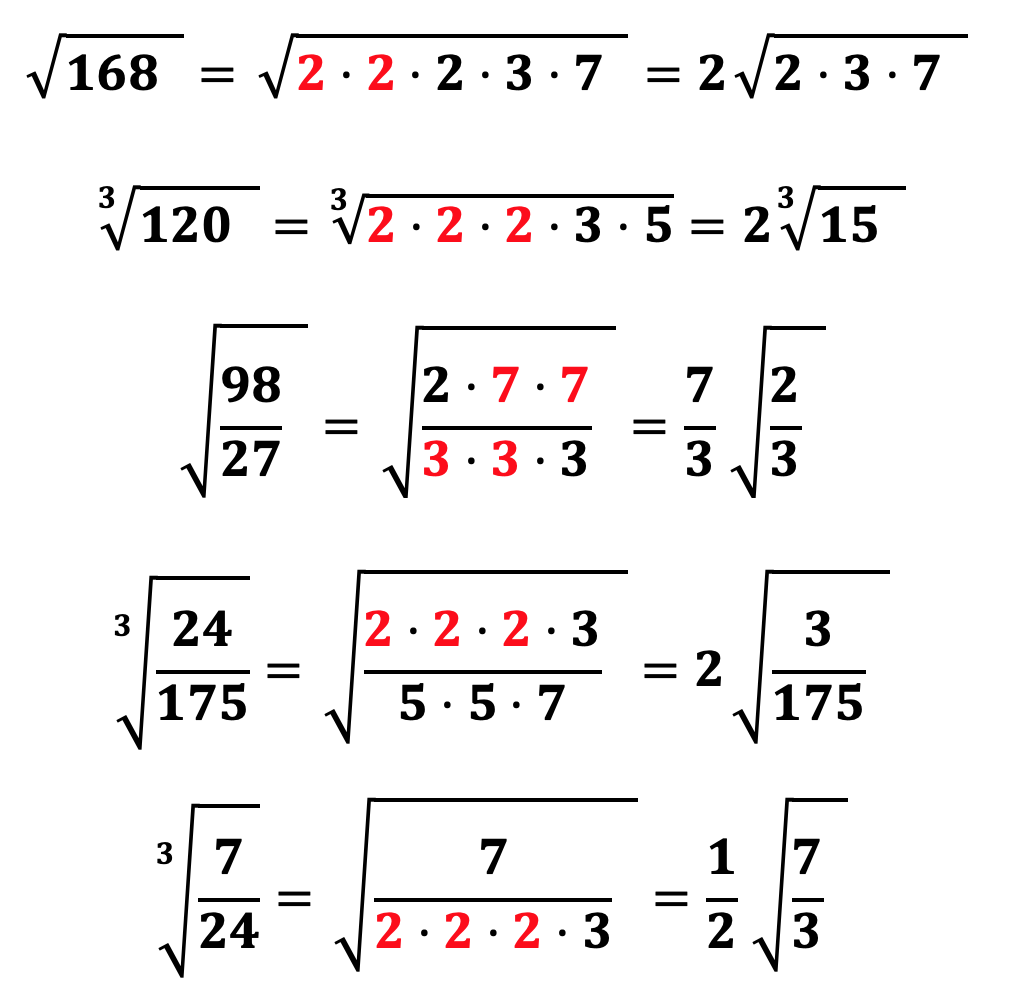
Как мы уже разобрали извлечь корень из числа а означает возведение числа a в дробную степень, числителем которой выступает степень числа a, а знаменателем – степень корня, поэтому следуя данному правилу мы легко выносим множители из под корня. Распишем предыдущие два примера еще раз:

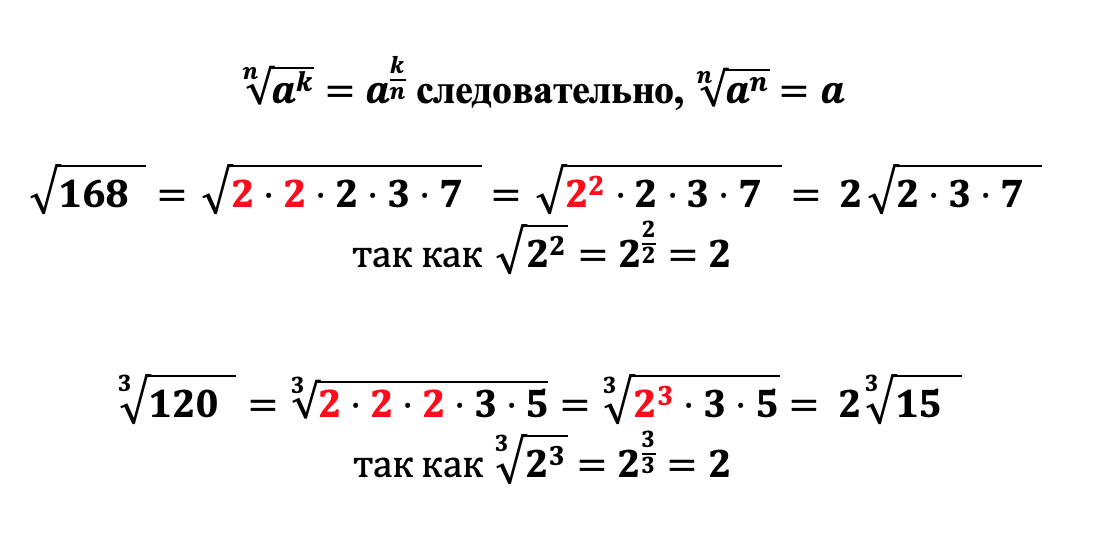
операций с квадратными корнями

Операции с квадратными корнями

Вы можете выполнить ряд различных операций с квадратными корнями. Некоторые из этих операций включают один радикальный знак, в то время как другие могут включать много радикальных знаков. Правила, регулирующие эти операции, должны быть тщательно рассмотрены.

Под одним радикальным знаком

Вы можете выполнять операции под одним радикальным знаком .

Пример 1

Выполните указанную операцию.

Когда радикальные ценности похожи

Вы можете добавлять или вычитать квадратные корни сами, только если значения под знаком радикала равны. Затем просто сложите или вычтите коэффициенты (числа перед знаком радикала) и оставьте исходное число в знаке радикала.

Пример 2

Выполните указанную операцию.

Обратите внимание, что коэффициент 1 понимается в .

Когда радикальные значения различны

Вы не можете добавлять или вычитать разные квадратные корни.

Пример 3

Сложение и вычитание квадратных корней после упрощения

Иногда, после упрощения квадратного корня (ов), становится возможным сложение или вычитание.Всегда упрощайте, если это возможно.

Пример 4

Упростите и добавьте.

Они не могут быть добавлены до упрощения .

Теперь, потому что оба одинаковы под знаком радикала,
Попробуйте упростить каждый.

Теперь, потому что оба одинаковы под знаком радикала,

Продукты неотрицательных корней

Помните, что при умножении корней знак умножения может быть опущен.Всегда упрощайте ответ, когда это возможно.

Пример 5

Умножить.

Если каждая переменная неотрицательна,
Если каждая переменная неотрицательна,
Если каждая переменная неотрицательна,

Коэффициенты неотрицательных корней

Для всех положительных чисел,

В следующих примерах все переменные предполагаются положительными.

Пример 6

Разделить. Оставьте все дроби с рациональными знаменателями.

Обратите внимание, что знаменатель этой дроби в части (d) иррациональный. Чтобы рационализировать знаменатель этой дроби, умножьте ее на 1 в форме

Пример 7

Разделить.Оставьте все дроби с рациональными знаменателями.

Первое упрощение :
или

Примечание: Чтобы оставить рациональный член в знаменателе, необходимо умножить числитель и знаменатель на сопряжение , знаменатель . Сопряжение бинома содержит те же термины, но противоположный знак.Таким образом, ( x + y ) и ( x — y ) являются сопряженными.

Пример 8

Разделить. Оставьте дробь с рациональным знаменателем.

Сложение и вычитание фракций (методы и примеры)

- Классы
  Класс 1 — 3
  Класс 4 — 5
  Класс 6 — 10
  Класс 11 — 12
- КОНКУРСЫ
  BBS
  000000000 Книги
  NCERT Книги для 5 класса
  NCERT Книги Класс 6
  NCERT Книги для 7 класса
  NCERT Книги для 8 класса
  NCERT Книги для 9 класса
  NCERT Книги для 10 класса
  NCERT Книги для 11 класса
  NCERT Книги для 12-го класса
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT Exemplar Class 12
  9000al Aggar Agaris Agard Agard Agard Agard Agard 2000 12000000
  Решения RS Aggarwal класса 10
  Решения RS Aggarwal класса 11
  Решения RS Aggarwal класса 10
  90 003 Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  Решения RD Sharma
  Решения класса RD Sharma
  Решения класса 9 Шарма 7 Решения RD Sharma Class 8
  Решения RD Sharma Class 9
  Решения RD Sharma Class 10
  Решения RD Sharma Class 11
  Решения RD Sharma Class 12
  ФИЗИКА
  Механика
  000000 Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  МАТС
  Теорема Пифагора
  Отношения и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Делительные дроби
  000 ФОРМУЛЫ
  Математические формулы
  Алгебровые формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  S000
  S0003
  Pегипс Класс 6
  Образцы документов CBSE для класса 7
  Образцы документов CBSE для класса 8
  Образцы документов CBSE для класса 9
  Образцы документов CBSE для класса 10
  Образцы документов CBSE для класса 11
  Образец образца CBSE pers for Class 12
  CBSE Документ с вопросами о предыдущем году
  CBSE Документы за предыдущий год Class 10
  CBSE Вопросы за предыдущий год Class 12
  HC Verma Solutions
  HC Verma Solutions Класс 11 Физика
  Решения HC Verma Class 12 Physics
  Решения Lakhmir Singh
  Решения Lakhmir Singh Class 9
  Решения Lakhmir Singh Class 10
  Решения Lakhmir Singh Class 8
  Примечания
  CBSE
  Notes
  CBSE Класс 7 Примечания CBSE
  Класс 8 Примечания CBSE
  Класс 9 Примечания CBSE
  Класс 10 Примечания CBSE
  Класс 11 Примечания CBSE
  Класс 12 Примечания CBSE
  Примечания пересмотра
  CBSE Редакция
  CBSE
  CBSE Class 10 Примечания к пересмотру
  CBSE Class 11 Примечания к пересмотру 9000 4
  Замечания по пересмотру CBSE класса 12
  Дополнительные вопросы CBSE
  Дополнительные вопросы CBSE 8 класса
  Дополнительные вопросы CBSE 8 по естественным наукам
  CBSE 9 класса Дополнительные вопросы
  CBSE 9 дополнительных вопросов по науке CBSE
  9000 Класс 10 Дополнительные вопросы по математике
  CBSE Класс 10 Дополнительные вопросы по науке
  Класс CBSE
  Класс 3
  Класс 4
  Класс 5
  Класс 6
  Класс 7
  Класс 8
  Класс 9
  Класс 10
  Класс 11
  Класс 12
  Решения для учебников
- Решения NCERT
  Решения NCERT для класса 11
  Решения NCERT для физики класса 11
  Решения NCERT для класса 11 Химия
  Решения для класса 11 Биология
  NCERT Решения для класса 11 Математика
  9 0003 NCERT Solutions Class 11 Бухгалтерия
  NCERT Solutions Class 11 Бизнес исследования
  NCERT Solutions Class 11 Экономика
  NCERT Solutions Class 11 Статистика
  NCERT Solutions Class 11 Коммерция
  NCERT Solutions для класса 12
  NCERT Solutions для Класс 12 Физика
  Решения NCERT для 12 класса Химия
  Решения NCERT для 12 класса Биология
  Решения NCERT для 12 класса Математика
  Решения NCERT Класс 12 Бухгалтерский учет
  Решения NCERT Класс 12 Бизнес исследования
  Решения NCERT Класс 12 Экономика
  NCERT Solutions Class 12 Бухгалтерский учет Часть 1
  NCERT Solutions Class 12 Бухгалтерский учет Часть 2
  NCERT Solutions Class 12 Микроэкономика
  NCERT Solutions Class 12 Коммерция
  NCERT Solutions Class 12 Макроэкономика
  NCERT Solutions Для Класс 4
  Решения NCERT для математики класса 4
  Решения NCERT для класса 4 EVS
  Решения NCERT для класса 5
  Решения NCERT для математики класса 5
  Решения NCERT для класса 5 EVS
  Решения NCERT для класса 6
  Решения NCERT для класса 6 Maths
  Решения NCERT для класса 6 Science
  Решения NCERT для класса 6 Общественные науки
  Решения NCERT для класса 6 Английский
  Решения NCERT для класса 7
  Решения NCERT для класса 7 Математика
  Решения NCERT для 7 класса Science
  Решения NCERT для 7 класса Общественные науки
  Решения NCERT для 7 класса Английский
  Решения NCERT для 8 класса Математические решения
  для 8 класса Математика
  Решения NCERT для класса 8 Science
  Решения NCERT для класса 8 Общественные науки
  NCERT Solutio ns для класса 8 Английский
  Решения NCERT для класса 9
  Решения NCERT для класса 9 Общественные науки
  Решения NCERT для класса 9 Математика
  Решения NCERT для класса 9 Математика Глава 1
  Решения NCERT Для класса 9 Математика 9 класса Глава 2
  Решения NCERT для математики 9 класса Глава 3
  Решения NCERT для математики 9 класса Глава 4
  Решения NCERT для математики 9 класса Глава 5
  Решения NCERT для математики 9 класса Глава 6
  Решения NCERT для Математика 9 класса Глава 7
  Решения NCERT для математики 9 класса Глава 8
  Решения NCERT для математики 9 класса Глава 9
  Решения NCERT для математики 9 класса Глава 10
  Решения NCERT для математики 9 класса Глава 11
  Решения NCERT для Математика 9 класса Глава 12
  Решения NCERT для математики 9 класса Глава 13
  Решения NCERT для математики 9 класса Глава 14
  Решения NCERT для математики класса 9 Глава 15
  Решения NCERT для науки 9 класса
  Решения NCERT для науки 9 класса Глава 1
  Решения NCERT для науки 9 класса Глава 2
  Решения NCERT для класса 9 Наука Глава 3
  Решения NCERT для 9 класса Наука Глава 4
  Решения NCERT для 9 класса Наука Глава 5
  Решения NCERT для 9 класса Наука Глава 6
  Решения NCERT для 9 класса Наука Глава 7
  Решения NCERT для 9 класса Научная глава 8
  Решения NCERT для 9 класса Научная глава
  Научные решения NCERT для 9 класса Научная глава 10
  Научные решения NCERT для 9 класса Научная глава 12
  Научные решения NCERT для 9 класса Научная глава 11
  Решения NCERT для 9 класса Научная глава 13
  Решения NCERT для 9 класса Научная глава 14
  Решения NCERT для класса 9 Science Глава 15
  Решения NCERT для класса 10
  Решения NCERT для класса 10 Общественные науки
  Решения NCERT для математики класса 10
  Решения NCERT для математики класса 10 Глава 1
  Решения NCERT для математики класса 10 Глава 2
  решения NCERT для математики класса 10 глава 3
  решения NCERT для математики класса 10 глава 4
  решения NCERT для математики класса 10 глава 5
  решения NCERT для математики класса 10 глава 6
  решения NCERT для математики класса 10 Глава 7
  решения NCERT для математики класса 10 глава 8
  решения NCERT для математики класса 10 глава 9
  решения NCERT для математики класса 10 глава 10
  решения NCERT для математики класса 10 глава 11
  решения NCERT для математики класса 10, глава 12
  Решения NCERT для математики класса 10, глава 13
  соль NCERT Решения для математики класса 10 Глава 14
  Решения NCERT для математики класса 10 Глава 15
  Решения NCERT для науки 10 класса
  Решения NCERT для науки 10 класса Глава 1
  Решения NCERT для науки 10 класса Глава 2
  Решения NCERT для науки 10 класса, глава 3
  Решения NCERT для науки 10 класса, глава 4
  Решения NCERT для науки 10 класса, глава 5
  Решения NCERT для науки 10 класса, глава 6
  Решения NCERT для науки 10 класса, глава 7
  Решения NCERT для науки 10 класса, глава 8
  Решения NCERT для науки 10 класса, глава 9
  Решения NCERT для науки 10 класса, глава 10
  Решения NCERT для науки 10 класса, глава 11
  Решения NCERT для науки 10 класса, глава 12
  Решения NCERT для 10 класса Science Глава 9
  Решения NCERT для 10 класса Science Глава 14
  Решения NCERT для науки 10 класса Глава 15
  Решения NCERT для науки 10 класса Глава 16
  Программа NCERT
  NCERT
- Коммерция
  Класс 11 Коммерческая программа Syllabus
  Учебный курс по бизнес-классу 11000
  Учебная программа по экономическому классу
- Учебная программа по коммерческому классу
  Учебная программа по 12 классу
  Учебная программа по 12 классу
  Учебная программа по экономическому классу
  000000000000000000
  Образцы коммерческих документов класса 11
  Образцы коммерческих документов класса 12
  Решения TS Grewal
  Решения TS Grewal Класс 12 Бухгалтерский учет
  Решения TS Grewal Класс 11 Бухгалтерский учет
  Отчет о движении денежных средств
  eurship
  Защита потребителей
  Что такое фиксированный актив
  Что такое баланс
  Формат баланса
  Что такое акции
  Разница между продажами и маркетингом
- P000S Документы ICSE
- ML Решения Aggarwal
  ML Решения Aggarwal Class 10 Maths
  ML Решения Aggarwal Class 9 Математика
  ML Решения Aggarwal Class 8 Maths
  ML Решения Aggarwal Class 7 Математические решения
  ML 6 0004
  ML 6
- Selina Solutions
  Selina Solution для 8 класса
  Selina Solutions для 10 класса
  Selina Solution для 9 класса 9
- Frank Solutions
  Frank Solutions для класса 10 Maths
  Frank Solutions для класса 9 Maths
- ICSE Class 9000 2
- ICSE Class 6
- ICSE Class 7
- ICSE Class 8
- ICSE Class 9
- ICSE Class 10
- ISC Class 11
- ISC Class 12

IAS

Сервисный экзамен

UPSC Syllabus

Бесплатно IAS Prep

Текущая информация

Список статей IAS

IAS 2019 Mock Test
IAS 2019 Mock Test 1
IAS 2019 Mock Test 2

KPSC KAS экзамен
UPPSC PCS экзамен
MPSC экзамен
RPSC RAS экзамен
TNPSC группа 1
APPSC группа 1
BPSC экзамен
экзамен
экзамен
WPSS
экзамен
WPSS
экзамен
JPS
экзамен
экзамен
PMS
экзамен
PMS
экзамен
экзамен
экзамен
9000

Вопросник UPSC 2019
Ключ ответа UPSC 2019

Коучинг IAS
IA S Коучинг Бангалор
IAS Коучинг Дели
IAS Коучинг Ченнаи
IAS Коучинг Хайдарабад
IAS Коучинг Мумбаи

JEE
Бумага
JEE JEE 9000
JEE
JEE-код
JEE-код
JEE J000
J0004 JEE
JEE Вопрос
Биномиальная теорема
JEE Статьи
Квадратичное уравнение

NEET
Программа Бьюя NEET
NEET 2020
NEET Приемлемость Критерии NEET 2020
S000
S000 образца
Поддержка
Жалоба Разрешение
Customer Care
Поддержка центр

Государственные платы
GSEB
GSEB Силабус
GSEB Вопрос бумаги
GSEB образец бумаги
GSEB Книги
90 004
MSBSHSE
MSBSHSE Syllabus

.
Бинарное сложение и вычитание — правила и примеры
Сложение и вычитание двоичной системы счисления аналогичны десятичной системе счисления. Единственное отличие состоит в том, что десятичная система счисления состоит из цифр от 0 до 9, а их основание равно 10, тогда как двоичная система счисления состоит только из двух цифр (0 и 1), которые облегчают их работу. Сложение и вычитание двоичных систем счисления подробно объясняется ниже.
Для понимания двоичное добавление сначала рассматривает добавление двух десятичных чисел, как показано ниже.
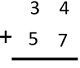Когда мы добавили один столбец двоичной цифры (т.е. 7 + 4), мы получим число, которое больше, чем основание десятичного числа (основание числа равно 10, а сумма цифры равна 11) , Теперь добавьте столбец десятков двоичной цифры, сумма которой равна 9 и, следовательно, меньше базовой. Таким образом, в столбце десяти двоичной цифры нет переноса.
Решение вышеуказанной суммы объясняется ниже.
Бинарное дополнение
Система двоичных чисел использует только две цифры 0 и 1, благодаря чему их сложение простое.Есть четыре основных операции для двоичного сложения, как упомянуто выше.
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
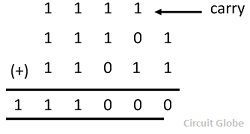
Вышеупомянутые первые три уравнения очень идентичны двоичному числу. Столбцовое сложение двоичного файла применяется ниже в деталях. Давайте рассмотрим добавление 11101 и 11011.
Вышеуказанная сумма выполняется следующим шагом
1 + 1 = 10 = 0 с переносом 1.
1 + 0 + 1 = 10 = 0 с переносом 1
1 + 1 + 0 = 10 = 10 = 0 с переносом 1
1 + 1 + 1 = 10 + 1 = 11 = 1 с переносом 1
1 +1 +1 = 11
Обратите внимание на , что 10 + 1 = 11, что эквивалентно двум + один = три (следующее двоичное число после 10)
Таким образом, требуемый результат составляет 111000.
Двоичное вычитание
Вычитание двоичной цифры зависит от четырех основных операций
0 — 0 = 0
1 — 0 = 1
1 — 1 = 0
10 — 1 = 1
Вышеупомянутые первые три операции легко понять, поскольку они идентичны десятичному вычитанию. Четвертая операция может быть понята с помощью логики два минус один — один.
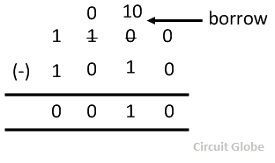
Для двоичного числа с двумя или более цифрами вычитание выполняется столбец за столбцом, как в десятичном вычитании.Кроме того, иногда нужно позаимствовать из следующего более высокого столбца. Рассмотрим следующий пример.
Вышеупомянутое вычитание выполнено через следующие шаги.
0 — 0 = 0
Для 0 — 1 = 1, брать заем 1, а затем 10 — 1 = 1
Для 1 — 0, поскольку 1 уже задано, оно становится 0 — 0 = 0
1 — 1 = 0
Следовательно, результат 0010.
,
Список онлайн-игр для сложения и вычитания и сложения / вычитания из нескольких цифр Вы здесь: Главная → Онлайн ресурсы → Сложение и вычитание
Это аннотированный и отобранный список онлайн-игр, инструментов, рабочих таблиц и действий, связанных с фактами сложения и вычитания или сложения / вычитания из нескольких цифр. Я пытался собрать различные ресурсы и лично подбирал каждый веб-сайт, чтобы убедиться, что он действительно полезен для посетителей моего сайта!

дополнения и дополнения факты
Упражнение «Суммы на автобусе»
«Суммы на автобусе» — это веселое сложение и вычитание для детского сада и первого класса, где вы добавляете людей в автобус, а также удаляете их на разных остановках.Дети могут практиковать простые задачи сложения и вычитания, наблюдая за ними в действии в реальном приложении.
/interactives/bus_sums_activity.php
K-Level Math
Практика счета, простого сложения и вычитания. В этой игре используются как цифры, так и цифры. Идеально подходит для детского сада.
www.smartygames.com/igre/game.php?dir=math&file=preKMath
Add — KidsCalculate
Практика сложного множественного выбора с интерактивными визуальными моделями — если ребенок не может ответить на проблему, ребенок может перетащить палки в рабочей области, чтобы найти ответ.Доступно несколько уровней (от 0 до 5, от 0 до 10, от 0 до 15, от 0 до 20 или от 0 до 50, добавьте к 5).
www.en.kidscalculate.com/MathBasics/BareBones/Math/ByCategory/Add
Дополнительное упражнение от Dositey.com
Напишите, сколько червей на двух листьях и сколько вместе.
www.dositey.com/2008/addsub/addex1.htm
Укладчик сумм
Перетаскивание кубиков из стека в стек до тех пор, пока суммы каждого стека не будут равны заданным суммам.
www.carstensstudios.com / mathdoodles / sumsstacker.html
Карточная игра сложения / вычитания
Эта карточная игра — простая, дешевая и забавная альтернатива бурению.
diosadotada.homeschooljournal.net/2008/05/15/easy-cheap-alternative-to-drill-kill
Веселая математическая карточная игра
Это не онлайн-игра, но объясняет простую и веселую карточную игру для сложения / вычитания.
blog.aussiepumpkinpatch.com/2010/03/meal-ticket-math.html
,
Навигация по записям
Previous Post:Дизайн комнаты с декоративным камнем: Декоративный камень в интерьере (90 фото)
Next Post:Гидроизоляция для крыши – Материалы для гидроизоляции кровли: какая гидроизоляция лучше?

Как складывать и вычитать квадратные корни

Теория складывания и вычитания квадратных корней

Как упростить подкоренное выражение

Подчеркиваем корни у которых одинаковы подкоренные выражения

Складываем или вычитаем наши корни

Как складывать квадратные корни

Шаг 1. Извлечение квадратных корней

Шаг 2. Вынесение множителя числа из-под корня

Шаг 3. Сокращение знаменателя

Пример сложного сокращения знаменателя

Шаг 4. Вычисление приблизительного значения на калькуляторе

Пример вычисления приблизительного значения

Правила сложения и вычитания квадратных корней

Действия с корнями: основы

Шаг 1. Извлечение квадратных корней

сложение и вычитание. Как вычесть корень из числа

Инструкция

Калькулятор корней с решением онлайн

Корень в математике

Четная и нечетная степень корня

Арифметический и алгебраический корни

Как упростить корень

операций с квадратными корнями

Операции с квадратными корнями

Под одним радикальным знаком

Пример 1

Когда радикальные ценности похожи

Пример 2

Когда радикальные значения различны

Пример 3

Сложение и вычитание квадратных корней после упрощения

Пример 4

Продукты неотрицательных корней

Пример 5

Коэффициенты неотрицательных корней

Пример 6

Пример 7

Пример 8

Сложение и вычитание фракций (методы и примеры)

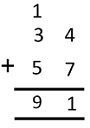<img decoding="async" src="/800/600/https/circuitglobe.com/wp-content/uploads/2016/09/decimal-equaiton-2.jpg" alt="decimal-equation-2" /> Бинарное дополнение

Двоичное вычитание

дополнения и дополнения факты

Leave a Reply Отменить ответ

Бинарное дополнение