Нет комментариев Разное

X 5 24 2 3 7 12: Решите уравненияа) x+5/24=2/3+7/12б)(3/8-х)-1/5=1/20 — ответ на Uchi.ru

Опубликовано

12. Уравнения, содержащие модуль. Рациональные уравнения

12. Уравнения, содержащие модуль. Рациональные уравнения

МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ

Уравнения, содержащие модуль

Если в уравнении некоторые выражения, содержащие неизвестное, стоят по знаком модуля, то решение исходного уравнения ищется отдельно на каждом из промежутков знакопостоянства этих выражений.

Пример 1
Решить уравнение |3x-6|=x+2.
Решение:
Рассмотрим первый случай: 3х-6≥0, тогда 3х-6=х+2, 2х=8, х=4.
Рассмотрим второй случай: 3х-6<0, тогда 3х-6=-(х+2), 4х=4, х=1.
Ответ: 1; 4.
 Пример 2
Решить уравнение |x-2| — 3|x-1| + 4|x-3| = 5.

Отметим на координатной прямой точки:х-2=0     х-1=0    х-3=0
х=2        х=1      х=3


Рассмотрим решения уравнения на промежутках (-∞; 1];   (1; 2];  (2; 3] и (3; +∞).

При х≤1: -(х-2) + 3(х-1) -4(х-3)=5, -х+2+3х-3-4х+12=5, -2х=-6, х=3.

Ответ не принадлежит промежутку, следовательно нет решений.
При 1<х≤2: -(х-2) — 3(х-1) -4(х-3)=5, -х+2-3х+3-4х+12=5, -8х=-12, х=1,5. Ответ принадлежит промежутку.
При 2<х≤3: х-2 — 3(х-1) -4(х-3)=5, х-2-3х+3-4х+12=5, -6х=-8, х=4/3. Ответ не принадлежит промежутку, следовательно нет решений.
При х>3: х-2 — 3(х-1) +4(х-3)=5, х-2-3х+3+4х-12=5, 2х=16, х=8. Ответ принадлежит промежутку.
Ответ: 1,5; 8.

Рациональные уравнения

  Рациональным уравнением называется уравнение вида 

где P(x), Q(x)  — многочлены.

Решение уравнения сводится к решению системы:

Пример 

Решить уравнение

Решение:

x2-4=0,                х-2≠0,

x

2=4,                   х≠ 2.

х=-2 или х=2.

Число 2 не может быть корнем.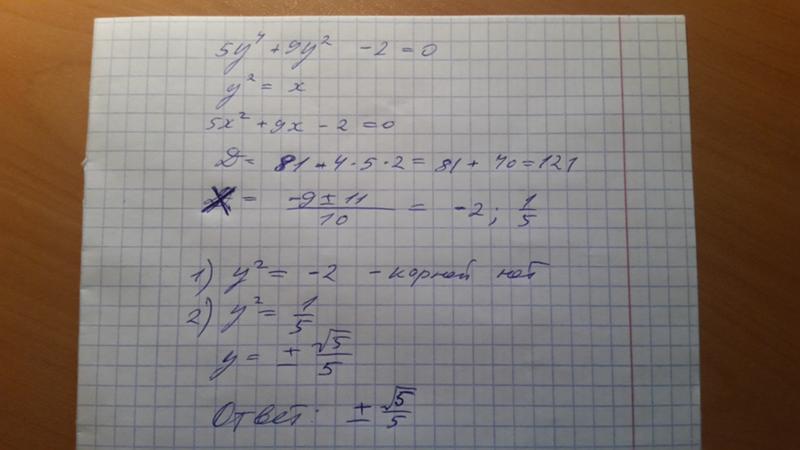

Ответ: -2.

УПРАЖНЕНИЯ

1. Из данных уравнений выберите те, которые не имеют корней:

а) |x|+4=1;    |x-5|=2;   |x+3|=-6.    б) |1+x|=3;   |1-x|=-4;   8+|x|=2.

Решение:
а)  |x|+4=1 не имеет корней, т.к.  |x|=-3 и модуль не может быть отрицательным числом; |x-5|=2 имеет корни; |x+3|=-6 не имеет корней, т.к.   модуль не может быть отрицательным числом.
Ответ: |x|+4=1; |x+3|=-6.


2. Решите уравнение:

а) |5x|=15;    б) |2x|=16.

Решение:
а) |5x|=15;
    |5||x|=15;


     5|x|=15;
     |x|=3;
     x=3 или x=-3.


3. Решите уравнение:

а) |5x+1|=5;    б) |2x-1|=10.

Решение:
а) |5x+1|=5;

Ответ: -1,2; 0,8.


4. Решите уравнение:

а) |5x2+3x-1|=-x2-36;    б) |3x2-5x-4|=-4x2-23.

Решение:
а) |5x2+3x-1|=-x2-36. Рассмотрим выражение  -x2-36, оно принимает отрицательные значения при любых значениях х, следовательно уравнение |5x2+3x-1|=-x2-36 не имеет корней.
Ответ: нет корней


5. Решите уравнение:

Решение:

Ответ: -1/3.

6. Решите уравнение:

Решение:

14х2-5x-1=0,

D=25+56=81,

x1=9/14;  x2=-1/7.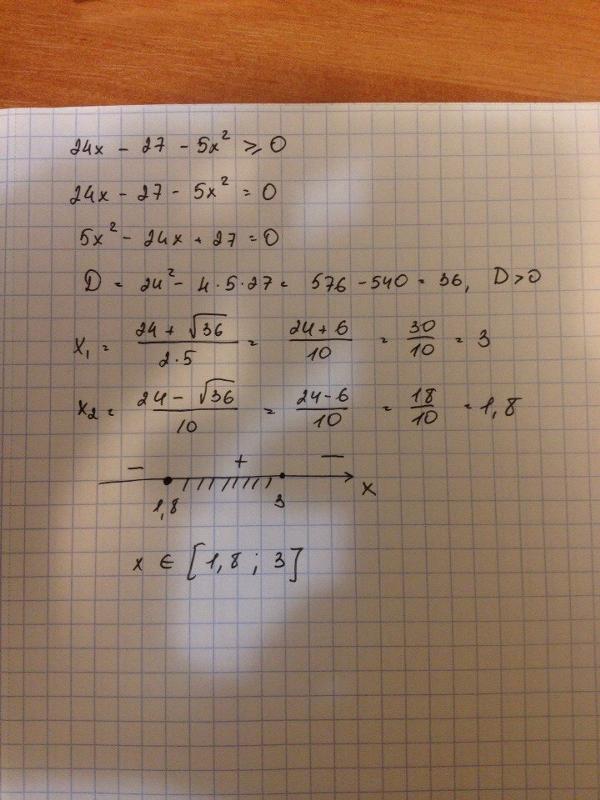

x≠2.


Ответ: -1/7; 9/14.

7. Решите уравнение:

Решение:



8. Решите уравнение:

Решение:

x2+3x-4=0,

D=9+16=25,


x1=1,  x2=-4.

х ≠3.

Ответ: -4; 1.

9. Найдите, при каком значении переменной значение выражения 

 равно:  а) -6;    б) 6.

Решение:

х2+7x+10=0,

D=49-40=9,

x1=-2;  x2=-5.

x≠-2.


Ответ: -5.

10. Решите уравнение:


Решение:
а) Разложим знаменатели на множители:
х2-36=(x-6)(x+6).
108-24x+х2=(x-6)(x-18).
2x-36=2(x-18).


11. Решите уравнение:

а) х2-6|x|=0;    б) х2+4|x|=0.   

Решение:

а) х2-6|x|=0; 
х≥0: х2-6x=0;   х(х-6)=0, x1=0, x2=6.

x<0:  х2+6x=0;   х(х+6)=0, x1=0, x2=-6.

Ответ: -6; 0; 6.

12.

Решите уравнение:

а) х2-3|x|+2=0;    б) х2-2|x|+1=0.   

Решение:

а) х2-3|x|+2=0.
х≥0: х2-3x+2=0;   D=9-8=1, x1=2, x2=1.
x<0:  х2+3x+2=0;   D=9-8=1, x1=-2, x2=-1.
Ответ: -2; -1; 1; 2.

13. Решите уравнение:

а) |x-2|+|x-4|=5;     б) |x-1|-|x-4|=6.

Решение:
а) |x-2|+|x-4|=5.
x≤2: -(x-2)-(x-4)=5, -x+2-x+4=5, x=0,5.
2<x≤4: x+2-(x-4)=5, x-2-x+4=5, 2=5 — нет решений.
x>4: x-2+x-4=5, 2x=11, x=5,5.

Ответ: 0,5; 5,5.

14.Решите уравнение:

а) |3- |4- |x|||=5;   б) 8-|2 -|x|||=3. 

Решение:
а) |3- |4- |x|||=5;
3- |4- |x||=5               или          3- |4- |x||=-5;
|4-|x||=-2 — нет решений            |4-|x||=8
                                                    4-|x|=8 или 4-|x|=-8
                                                    |x|=-4 — нет решений   |x|=12
                                                                                         х=12 или х=-12.
Ответ: -12; 12.


15. Решите уравнение:

Решение:
а) 
3x-7≥0: х2-3x+10=0;   D=9-40=-31<0 — нет корней.

3x-7<0: х2-3x-10=0;   D=9+40=49, x1=5, x2=-2.
3x-7≠0, x≠7/3.
Ответ: -2; 5.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Какие из чисел -4; -1;  2;  1,5; 2,5 являются корнями уравнения:

а) |3x-1|=5;    б) |4-2x|=1?

2. Решите уравнение:

а) |3x|=21;    б) |2x|=-12.

3.  Решите уравнение:

а) |2x-5|=1;    б) |3x+6|=18.

4.  Решите уравнение:

5.  Решите уравнение:

6.  Решите уравнение:

7.  Решите уравнение:

8.  Решите уравнение:

9. Решите уравнение:

а) 3(x-1) = |2x-1|;   б) |5-2x|=|x+4|.

10. Решите уравнение:

а) |х2+x|=12;    б) |х2-3x|=10.

Проверь себя



Подписаться на: Сообщения (Atom)

Аналитические вестники | Совет Федерации Федерального Собрания Российской Федерации

  • Аналитические вестники
  • Аналитические доклады
  • Издания Совета Федерации

3 (823) Февраль 2023 «Современное состояние и перспективы социально-экономического развития Владимирской области»

2 (822) Январь 2023 «Современное состояние и перспективы социально-экономического развития Архангельской области»

1 (821) Январь 2023 «Современное состояние и перспективы социально-экономического развития Архангельской области»

30 (820) Декабрь 2022 «Современное состояние и перспективы социально-экономического развития Республики Саха (Якутия)

29 (819) Декабрь 2022 «Современное состояние и перспективы социально-экономического развития Республики Саха (Якутия)»

28 (818) Ноябрь 2022 «Современное состояние и перспективы социально-экономического развития Новгородской области»

27 (817) Ноябрь 2022 «Современное состояние и перспективы социально-экономического развития Новгородской области»

26 (816) Ноябрь 2022 «IT-отрасль: состояние, проблемы, перспективы»

25 (815) Октябрь 2022 «Участие бизнеса в развитии социальной сферы: новые подходы и решения»

23 (813) Октябрь 2022 «Современное состояние и перспективы социально-экономического развития Омской области»

22 (812) Октябрь 2022 «О реализации доктрины продовольственной безопасности Российской Федерации»

21 (811) Октябрь 2022 «Современное состояние и перспективы социально-экономического развития Омской области»

20 (810) Сентябрь 2022 «Современное состояние и перспективы социально-экономического развития Иркутской области»

19 (813) Сентябрь 2022 «Создание условий для занятий физической культурой и спортом инвалидов, включая детей-инвалидов, и лиц с ограниченными возможностями здоровья: итоги 2021 года и основные мероприятия на 2022 год»

18 (808) Сентябрь 2022 «Современное состояние и перспективы социально-экономического развития Иркутской области»

17 (807) Июль 2022 «Современное состояние и перспективы социально-экономического развития Республики Адыгея»

16 (806) Июль 2022 «Современное состояние и перспективы социально-экономического развития Республики Адыгея»

15 (805) Июнь 2022 «Современное состояние и перспективы социально-экономического развития города федерального значения Севастополя»

14 (804) Июнь 2022 Современное состояние и перспективы социально-экономического развития Ленинградской области

13 (803) Июнь 2022 «Современное состояние и перспективы социально-экономического развития города федерального значения Севастополя»

12 (802) Май 2022 «Современное состояние и перспективы социально-экономического развития Ленинградской области»

11 (801) Май 2022 «О мерах по поддержке занятости в условиях новых вызовов»

10 (800) Апрель 2022 «Роль прорывных медицинских технологий в условиях новых вызовов»

9 (799) Март 2022 «Проблемы социально-медицинской реабилитации граждан, перенесших новую коронавирусную инфекцию (COVID-19)»

8 (798) Март 2022 «Современное состояние и перспективы социально-экономического развития города федерального значения Севастополя»

7 (797) Февраль 2022 «Современное состояние и перспективы социально-экономического развития Республики Бурятия»

5 (795) Февраль 2022 «Актуальные вопросы трудоустройства инвалидов после получения ими образования»

3 (793) Февраль 2022 «О реализации региональных программ модернизации первичного звена здравоохранения»

2 (792) Февраль 2022 «К 350-летию со дня рождения Петра I: секулярный мир и религиозность»

1 (791) Январь 2022 «Современное состояние и перспективы социально-экономического развития Республики Бурятия»

Показать предыдущие материалы

Калькулятор дробей


Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.

Правила выражения с дробями:

Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.

Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .

Math Symbols


Symbol Symbol name Symbol Meaning Example
+ plus sign addition 1/2 + 1/3
— знак минус вычитание 1 1/2 — 2/3
* asterisk multiplication 2/3 * 3/4 ​​
× times sign multiplication 2 /3 × 5/6
: division sign division 1/2 : 3
/ division slash division 1/3 / 5 1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4 ​​
• квадратный корень дроби: sqrt(1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3

Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание
BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание.
GEMDAS — Символы группировки — скобки (){}, возведения в степень, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будьте осторожны; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.

  • Саманта
    Саманта сделала 72 снимка во время пляжного отдыха. 3/4 этих фотографий на пляже. Сколько фотографий с ее отпуска на пляже?
  • Энди набрал
    Энди неправильно ответил на пять из 15 вопросов в тесте по математике. На какую часть вопроса Энди ответил правильно?
  • Следующие 3
    Следующая дробь сокращена до наименьшего члена, кроме единицы. Какой из них: А.98/99 B.73/179 C.1/250 D.81/729
  • Компания
    В компании работает 860 человек, из которых 500 женщин. Напишите дробь, обозначающую сотрудниц компании.
  • Десятичная дробь
    Запишите дробь 3/22 в виде десятичной дроби.
  • Мэтью
    У Мэтью восемь карандашей. У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце?
  • Значение Z
    При x = -9, каково значение Z, где Z равно числителю дроби x минус 17 в знаменателе 6,5 конец дроби Дайте ответ с точностью до 2 знаков после запятой.
  • Коричневый или черный
    У Макса 13 пар носков. Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?
  • Использование денег
    Из 575 000,00, отданных школе, было использовано 25 000,00. Какая часть от общей суммы была использована?
  • Дробь и десятичная дробь
    Пишите в виде дроби и десятичной дроби. Один и два плюс три и пять сотых
  • Упрощение 12
    Упростить {1/3 + 1/12} ÷ {2/3 — 5/8}

Подробнее по математике »

  • Десятиц
  • Фракции
  • Triangle ΔABC
  • %
  • 066666066206206206206206206206206062062060620620620620620620620606ERLILL factors
  • complex numbers
  • LCM
  • GCD
  • LCD
  • combinatorics
  • equations
  • statistics
  • … all maths calculators

Fraction calculator


Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.

Правила выражений с дробями:

Дроби — для деления числителя на знаменатель используйте косую черту, т. е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.

Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .

Math Symbols


91/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4 ​​
• квадратный корень дроби: sqrt(1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3

Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание
BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание.
GEMDAS — Символы группировки — скобки (){}, возведения в степень, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будьте осторожны; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.

  • Саманта
    Саманта сделала 72 снимка во время пляжного отдыха. 3/4 этих фотографий на пляже. Сколько фотографий с ее отпуска на пляже?
  • Энди набрал
    Энди неправильно ответил на пять из 15 вопросов в тесте по математике. На какую часть вопроса Энди ответил правильно?
  • Следующие 3
    Следующая дробь сокращена до наименьшего члена, кроме единицы. Какой из них: А.98/99 B.73/179 C.1/250 D.81/729
  • Компания
    В компании работает 860 человек, из которых 500 женщин. Напишите дробь, обозначающую сотрудниц компании.
  • Десятичная дробь
    Запишите дробь 3/22 в виде десятичной дроби.
  • Мэтью
    У Мэтью восемь карандашей. У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце?
  • Значение Z
    При x = -9, каково значение Z, где Z равно числителю дроби x минус 17 в знаменателе 6,5 конец дроби Дайте ответ с точностью до 2 знаков после запятой.
  • Коричневый или черный
    У Макса 13 пар носков. Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?
  • Использование денег
    Из 575 000,00, отданных школе, было использовано 25 000,00. Какая часть от общей суммы была использована?
  • Дробь и десятичная дробь
    Пишите в виде дроби и десятичной дроби.

    Leave a Reply

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

Symbol Symbol name Symbol Meaning Example
+ plus sign addition 1/2 + 1/3
— знак минус вычитание 1 1/2 — 2/3
* asterisk multiplication 2/3 * 3/4 ​​
× times sign multiplication 2/3 × 5/6
: division sign division 1/2 : 3
/ division slash division 1/3 / 5