Калькулятор онлайн — Перевод конечной и бесконечной периодической десятичной дроби в обыкновенную
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Обыкновенные дроби. Деление с остатком
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель.
Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний
компонент, которого нет в обычном делении, — остаток. В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое
В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление.
Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\( m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a : m}{b : m} \)
Это свойство называют основным свойством дроби.
Два последних преобразования называют сокращением дроби.
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю.
Правильные и неправильные дроби. Смешанные числа
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например,
дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались
для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими
дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби,
у которых числитель больше знаменателя или равен ему, называют неправильными дробями. Остальные дроби, т. е. дроби, у которых
числитель меньше знаменателя, называют правильными дробями.
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными.
Например:
Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\( \large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
\( \large \frac{a}{b} : n = \frac{a}{bn} \)
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \). Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть.
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
С помощью букв это правило записывается так:
\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное
свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \). Эту дробь называют обратной дроби \( \frac{2}{3} \).
Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как \( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.
Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.
Как перевести десятичную дробь в обыкновенную: 3 способа
Вот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду.
Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная. Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:
\[0,75=\frac{3}{4};\quad 1,33=1\frac{33}{100};\quad -7,41=-7\frac{41}{100}\]
Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро?
Основной алгоритм
На самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.
И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.
Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:
- Переписать исходную дробь в виде новой дроби: в числителе останется исходная десятичная дробь, а в знаменателе нужно поставить единицу. При этом знак исходного числа также помещается в числитель. Например:
\[0,75=\frac{0,75}{1};\quad 1,33=\frac{1,33}{1};\quad -7,41=\frac{-7,41}{1}\]
- Умножаем числитель и знаменатель полученной дроби на 10 до тех пор, пока в числителе не исчезнет запятая. Напомню: при каждом умножении на 10 запятая сдвигается вправо на один знак. Разумеется, поскольку знаменатель тоже умножается, там вместо числа 1 будут появляться 10, 100 и т.д. Примеры: Алгоритм перехода к обычным дробям
- Наконец, сокращаем полученную дробь по стандартной схеме: делим числитель и знаменатель на те числа, которым они кратны. Например, в первом примере 0,75=75/100, при этом и 75, и 100 делятся на 25.
 Поэтому получаем $0,75=\frac{75}{100}=\frac{3\cdot 25}{4\cdot 25}=\frac{3}{4}$ — вот и весь ответ.:)
Поэтому получаем $0,75=\frac{75}{100}=\frac{3\cdot 25}{4\cdot 25}=\frac{3}{4}$ — вот и весь ответ.:)
Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». Вот ещё несколько примеров:
Примеры перехода от десятичной записи дробей к обычнойОсобое внимание хотелось бы обратить на последний пример. Как видим, в дроби 0,0025 присутствует много нулей после запятой. Из-за этого приходится аж целых четыре раза умножать числитель и знаменатель на 10. Можно ли как-то упростить алгоритм в этом случае?
Конечно, можно. И сейчас мы рассмотрим альтернативный алгоритм — он чуть более сложен для восприятия, но после небольшой практики работает намного быстрее стандартного.
Более быстрый способ
В данном алгоритме также 3 шага. Чтобы получить обычную дробь из десятичной, нужно выполнить следующее:
- Посчитать, сколько цифр стоит после запятой.
 {3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.Наконец, последний пример:
\[1,88=\frac{188}{100}=\frac{47}{25}=\frac{25+22}{25}=1\frac{22}{25}\]
Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.
Что делать с целой частью
На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.
Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88.
 Она легко преобразуется:
Она легко преобразуется:\[0,88=\frac{88}{100}=\frac{22}{25}\]
Затем вспоминаем про «утерянную» единицу и дописываем её спереди:
\[\frac{22}{25}\to 1\frac{22}{25}\]
Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:
\[\begin{align}& 2,15\to 0,15=\frac{15}{100}=\frac{3}{20}\to 2\frac{3}{20}; \\& 13,8\to 0,8=\frac{8}{10}=\frac{4}{5}\to 13\frac{4}{5}. \\\end{align}\]
В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)
В заключение хотел бы рассмотреть ещё один приём, который многим помогает.
Преобразования «на слух»
Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.
А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных».
 Так или иначе, ключевое слово — «тысячных», т.е. 1000.
Так или иначе, ключевое слово — «тысячных», т.е. 1000.Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:
\[0,004=4:1000=\frac{4}{1000}=\frac{1}{250}\]
Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
\[2,5=2\frac{5}{10}=2\frac{1}{2}\]
А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому
\[1,125=1\frac{125}{1000}=1\frac{1}{8}\]
В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 103, а 10 = 2 ∙ 5, поэтому
\[\begin{align}& 1000=10\cdot 10\cdot 10=2\cdot 5\cdot 2\cdot 5\cdot 2\cdot 5= \\& =2\cdot 2\cdot 2\cdot 5\cdot 5\cdot 5=8\cdot 125\end{align}\]
Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.

На этом урок окончен. Переходим к более сложной обратной операции — см. «Переход от обыкновенной дроби к десятичной».
Смотрите также:
- Сравнение дробей
- Периодические десятичные дроби
- Пробный ЕГЭ 2012 от 7 декабря. Вариант 3 (без логарифмов)
- Метод Гаусса
- Интегрирование по частям
- Задача B4: обмен валют в трех различных банках
Перевод десятичных чисел в дробь: онлайн калькулятор
Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.
Представление дробей
Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:
- 0,5 = 1/2;
- 0,25 = 1/4;
- 1,375 = 11/8.

И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.
Избавляемся от запятой
Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:
Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.
Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:
- 0,5/1 = 5/10;
- 0,25/1 = 2,5/10 = 25/100;
- 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.
Шаг 3: Сокращаем полученные дроби до удобоваримого вида:
- 5/10 = 1 × 5 / 2 × 5 = 1/2;
- 25/100 = 1 × 25 / 4 × 25 = 1/4;
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8.

Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.
Избавляемся от запятой еще проще
Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.
Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.
Шаг 2: Теперь нам достаточно представить дробь в виде C/10n, где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:
- для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/103 = 1375/1000;
- для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/106 = 625/1000000.

По сути, 10n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.
Шаг 3: Сокращаем нули и получаем итоговый результат:
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.
Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
Преобразование на слух
Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.
0,025 = 25/1000 = 1/40
Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.

Примеры использования дробей в повседневной жизни
На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.
Работа
Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.
0,4 = 4/10 = 2/5
Быт
К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:
0,12 = 12/100 = 3/25
Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.

Заключение
Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.
Десятичные дроби — как решать примеры 5, 6 класс
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
Основные свойства - Дробь не имеет значения, при условии, если делитель равен нулю.

- Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
- Две дроби a/b и c/d называются равными, если a * d = b * c.
- Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Как решаем:
- Знаменатель равен 10 — это один ноль.
- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Ответ: 16/10 = 1,6.
Пример 2. Перевести 37/1000 в десятичную дробь.
Как решаем:
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
Сколько цифр после запятой? Читается, как одна цифра — десятых; 1,3 — одна целая, три десятых; две цифры — сотых 2,22 — две целых, двадцать две сотых; три цифры — тысячных; 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; четыре цифры — десятитысячных; 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; и т.  д.
д.Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
1% = 1/100 = 0,01
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
0,15 = 0,15 · 100% = 15%.
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%8/25 = 0,32
0,32 · 100% = 32%Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого.
 Наглядная табличка — наш друг-помощник:
Наглядная табличка — наш друг-помощник:Преобразование десятичных дробей
Быстрая напоминалка:
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Как решаем:
- Читаем вслух: пять целых четыре десятых. «Четыре десятых» подсказывают, что в числителе будет 4, а в знаменателе — 10. В смешанном виде эта дробь выглядит так: 5 4/10.
- А теперь сократим числитель и знаменатель на два (потому что можно) и получим: 5 2/5.
Ответ: 5,4 = 5 2/5.
Пример 2.
 Перевести 4,005 в смешанное число.
Перевести 4,005 в смешанное число.Как решаем:
- Читаем вслух: четыре целых пять тысячных. Значит 5 — идет в числитель, а 1000 — в знаменатель. В смешанном виде получается так: 4 5/1000. После сокращения: 4 1/200.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как решаем:
- Читаем вслух: пять целых шестьдесят сотых. Отправляем 60 в числитель, а 100 — в знаменатель. В смешанном виде дробь такая: 5 60/100.
- Сократим дробную часть на 10 и получим 5 6/10. Или можно вспомнить про свойство десятичной дроби и просто отбросить нули в числителе и знаменателе.
Ответ: 5,60 = 5 6/10.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу.
 Например:
Например:- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
- Разделить целую часть десятичной дроби на это число.

- Поставить запятую в частном и продолжить вычисление, как при обычном делении.
Как решаем:
- Записать деление уголком.
- Разделить целую часть на два. Записать полученный результат в частное и поставить запятую.
- Умножить частное на делитель, записать, посмотреть на остаток от деления. Но мы еще не закончили, поэтому остаток «ноль» не записываем. Сносим 8 и делим её на 2.
- Делим еще раз. Записываем полученную 4 в частном и умножаем её на делитель:
Ответ: 4,8 : 2 = 2,4.
Пример 2. Разделить 183,06 на 45.
Как решаем:
- Записать деление уголком.
- Разделить целую часть 183 на 45. Записать результат, поставить запятую в частном.
- Записать результат разницы 183 и 180. Снести 0. Записать 0 в частное, чтобы снести 6.
- Записать результат разницы 306 и 270. 36 не делится на 45, поэтому добавляем ноль и производим разницу.
Ответ: 183,06 : 45 = 4,068.

Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.Как решаем:
- Записать 0,25 в виде обыкновенной дроби: 0,25 = 25/100.
- Разделить дробь по правилам:
Ответ: 0,25 : 3/4 = 1/3.
Пример 2. Разделить 2,55 на 1 1/3.
Как решаем:
- Записать 2,55 в виде обыкновенной дроби: 2,55 = 255/1000.
- Записать 1 1/3 в виде обыкновенной дроби: 1 1/3 = 4/3.
- Разделить дробь по правилам:
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Как решаем:
- Записать 0,8 в виде обыкновенной дроби: 0,8 = 8/10.
- Умножаем по правилам: 2/5 ∗ 8/10 = 2/5 ∗ 4/5 = 8/25 = 0,32.
Ответ: 2/5 ∗ 0,8 = 0,32.
Пример 2. Умножить 0,28 на 6 1/4.
Как решаем:
- Записать 6 1/4 в виде десятичной дроби: 6 1/4 = 6,25.
- Умножаем по правилам: 0,28 ∗ 6,25 = 0,8.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Калькулятор дробей
Как перевести смешанную дробь в обыкновенную
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: i nd = i · d + nd
Например,
5 34 = 5 · 4 + 34 = 234Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
- Поделить числитель дроби на её знаменатель
- Результат от деления будет являться целой частью
- Остаток отделения будет являться числителем
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.

Как перевести десятичную дробь в обыкновенную или смешанную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
- Записать дробь в виде десятичная дробь1
- Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
- Найти наибольший общий делитель и сократить дробь.
Например, переведем 0.36 в обыкновенную дробь:
- Записываем дробь в виде: 0.361
- Умножаем на 10 два раза, получим 36100
- Сокращаем дробь 36100 = 925
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).

- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Выполнить сложение дробей путем сложения их числителей.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.

- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Умножение дробей
Алгоритм действий при умножении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Деление дробей
Алгоритм действий при делении двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
- Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.

- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Дроби
Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.
Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.
Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.
А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.
Что такое дробь?Если говорить простым языком, то дробь это часть чего-либо.
 Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.
Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.
Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.
Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:
Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:
А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:
Такие записи называют дробями.
 Дробь состоит из числителя и знаменателя.
Дробь состоит из числителя и знаменателя.Число, которое записывается сверху, называется числителем дроби.
Число, которое записывается снизу, называется знаменателем дроби.
В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы.
Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь?
Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):
Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли».
Теперь представьте, что пиццу мы разделили не на четыре части, а на три.
Допустим мы съели один кусок этой пиццы.
 Как записать такую дробь?
Как записать такую дробь?Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:
Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть».
Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:
Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам»:
Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь?
Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:
Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».

Дроби, которые мы сейчас рассмотрели, называют обыкновенными.
Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.
Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.
На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.
Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли (одну часть из двух), или как говорят в народе «половину» пиццы.

С помощью переменных дробь можно записать так:
где a — это числитель, b — знаменатель.
Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными.
Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:
Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём (одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.
С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:
Видно, что у этих дробей числитель больше знаменателя.
 Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.Теперь возьмём к примеру неправильную дробь и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:
Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь . Применим её к нашей пицце.
Допустим, мы хотим съестьпиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим этупиццы, то съедим не часть пиццы, а всю пиццу целиком.
 Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
Дробь означает делениеЧерта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.
Например, рассмотрим дробь . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:
Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».
Выделение целой части дроби
Вычислим дробь . Пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Проверка: (2 × 2) + 1 = 4 + 1 = 5
Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде.
 Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.
Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?
Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:
Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока.
Теперь возвращаемся к дроби и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:
Схематически это выглядит так:
Процедуру, которую мы сейчас провели, называют выделением целой части дроби.
В нашем примере мы выделили целую часть дроби и получили новую дробь .
 Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.
Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.В нашем примере целая часть это 2, а дробная часть это
Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.
Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть:
Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби . Записываем уголком данное выражение и решаем:
После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Важно понимать, что куда относить. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.
В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком.
 В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.
В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.
Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби
Записываем уголком данное выражение и решаем. Потом собираем смешанную дробь:
Получили:
Перевод смешанного числа в неправильную дробьЛюбое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь . Если выделить в ней целую часть, то получается
Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученный результат будет числителем новой дроби, а знаменатель останется без изменений.

Например, переведём смешанное число в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:
2 × 3 = 6
Затем к 6 прибавляем числитель дробной части:
6 + 1 = 7
Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменений:
Подробное решение выглядит так:
А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:
Пример 2. Перевести смешанное число в неправильную дробь.
Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений:
Основное свойство дробиОсновное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.
Например, рассмотрим дробь .
 Умножим её числитель и знаменатель на одно и то же число, например на число 2
Умножим её числитель и знаменатель на одно и то же число, например на число 2Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (один кусок из двух), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.
Рассмотрим дробь . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2
Получили новую дробь .
 Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (четыре куска из восьми), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.
Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!
Сокращение дробейДроби можно сокращать.
 Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь .
Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь .Если при решении примеров получается большая и некрасивая дробь, то нужно попытаться её сократить.
Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.
Деление числителя и знаменателя на их наибольший общий делитель называется сокращением дроби.
Пример 1. Сократить дробь
Итак, нужно разделить числитель и знаменатель дроби на наибольший общий делитель чисел 2 и 4.
В данном случае дробь простая и для неё НОД ищется легко. НОД чисел 2 и 4 это число 2. Значит, числитель и знаменатель дроби надо разделить на 2
В результате дробь обратилась в более простую дробь . Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число.
 А это действие, как было указано ранее, не меняет значение дроби.
А это действие, как было указано ранее, не меняет значение дроби.На рисунке представлены дроби и в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.
Пример 2. Сократим дробь
Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.
НОД чисел 20 и 40 это число 20. Поэтому делим числитель и знаменатель дроби на 20
Пример 3. Сократим дробь
Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.
НОД чисел 32 и 36 это число 4. Поэтому делим числитель и знаменатель дроби на 4
Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:
Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.

Второй способ сокращения дроби
Второй способ является короткой версией первого способа. Суть его заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.
К примеру, вернёмся к дроби . Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4
Теперь представьте, что в данном выражении отсутствует конструкция , и сразу записан ответ . Получится следующее выражение:
Суть в том что число, на которое разделили числитель и знаменатель, хранят в уме. В нашем случае числитель и знаменатель делят на 4 — это число и будем хранить в уме.
Сначала делим числитель на число 4. Полученный ответ записываем рядом с числителем, предварительно зачеркнув его:
Затем таким же образом делим знаменатель на число 4. Полученный ответ записываем рядом со знаменателем, предварительно зачеркнув его:
Затем собираем новую дробь. В числитель отправляем новое число 8 вместо 32, а в знаменатель отправляем новое число 9 вместо 36
Происходит своего рода замена одной дроби на другую.
 Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель.
Например, сократим дробь , предварительно разложив на простые множители числитель и знаменатель:
Итак, мы разложили числитель и знаменатель дроби на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.
Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение:
Сократить можно ещё по тройке в числителе и в знаменателе:
Дальше сокращать больше нéчего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, который можно было бы сократить вместе с этой тройкой.

Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.
Получили ответ . Значит, при сокращении дроби получается новая дробь .
Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если человек только нáчал изучать математику. Практика показывает, что это оказывается сложным на первых этапах.
Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решён старым способом и будет выглядеть так:
Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом:
Первое выражение намного понятнее, аккуратнее и короче. Не правда ли?
Задания для самостоятельного решенияЗадание 1.
 Запишите в виде дроби следующий рисунок:
Запишите в виде дроби следующий рисунок:Задание 2. Запишите в виде дроби следующий рисунок:
Задание 3. Запишите в виде дроби следующий рисунок:
Задание 4. Запишите в виде дроби следующий рисунок:
Задание 5. Запишите в виде дроби следующий рисунок:
Задание 6. Выделите целые части в следующих дробях:
Задание 7. Выделите целые части в следующих дробях:
Задание 8. Переведите смешанные дроби в неправильные:
Задание 9. Переведите смешанные дроби в неправильные, не расписывая как целая часть умножается на знаменатель дробной части и полученный результат складывается с числителем дробной части
Задание 10. Сократите следующую дробь на 3
Задание 11. Сократите следующую дробь на 3 вторым способом
Задание 12. Сократите следующую дробь на 5
Задание 13. Сократите следующую дробь на 5 вторым способом
Задание 14. Сократите следующие дроби:
Задание 15.
 Сократите следующие дроби вторым способом:
Сократите следующие дроби вторым способом:Задание 16. Запишите в виде дроби следующий рисунок:
Задание 17. Запишите в виде дроби следующий рисунок:
Задание 18. Запишите в виде дроби следующий рисунок:
Задание 19. Запишите в виде дроби следующий рисунок:
Задание 20. Запишите в виде дроби следующий рисунок:
Задание 21. Изобразите в виде рисунка следующую дробь:
Задание 22. Изобразите в виде рисунка следующую дробь:
Задание 23. Изобразите в виде рисунка следующую дробь:
Задание 24. Изобразите в виде рисунка следующую дробь:
Задание 25. Изобразите в виде рисунка следующую дробь:
Задание 26. Изобразите в виде рисунка следующую дробь:
Задание 27. Изобразите в виде рисунка следующую дробь:
Задание 28. Изобразите в виде рисунка следующую дробь:
Задание 29. Изобразите в виде рисунка следующую дробь:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых урокахВозникло желание поддержать проект?
Используй кнопку нижеНавигация по записям
правила, примеры, решения, как умножать десятичные дроби
В этой статье мы рассмотрим такое действие, как умножение десятичных дробей.
 Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100, 10 и др.)
Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100, 10 и др.)В рамках этого материала мы коснемся только правил умножения положительных дробей. Случаи с отрицательными разобраны отдельно в статьях об умножении рациональных и действительных чисел.
Умножение десятичных дробей: общие принципы
Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.
Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.

Посмотрим, как решаются такие задачи.
Пример 1Вычислите произведение 1,5 и 0,75.
Решение: для начала заменим десятичные дроби на обыкновенные. Мы знаем, что 0,75 – это 75/100, а 1,5 – это 1510. Мы можем сократить дробь и произвести выделение целой части. Полученный результат 1251000 мы запишем как 1,125.
Ответ: 1,125.
Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.
Пример 2Умножьте одну периодическую дробь 0,(3) на другую 2,(36).
Решение
Для начала приведем исходные дроби к обыкновенным. У нас получится:
0,(3)=0,3+0,03+0,003+0,003+…=0,31-0,1=0,39=39=132,(36)=2+0,36+0,0036+…=2+0,361-0,01=2+3699=2+411=2411=2611
Следовательно, 0,(3)·2,(36)=13·2611=2633.
Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:
Ответ: 0,(3)·2,(36)=0,(78).
Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см.
Пример 3 статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.
статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.Вычислите произведение 5,382… и 0,2.
Решение
У нас в задаче есть бесконечная дробь, которую нужно предварительно округлить до сотых. Получится, что 5,382…≈5,38. Второй множитель округлять до сотых смысла не имеет. Теперь можно подсчитать нужное произведение и записать ответ: 5,38·0,2=538100·210=1 0761000=1,076.
Ответ: 5,382…·0,2≈1,076.
Как умножать десятичные дроби столбиком
Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:
Определение 1Умножение десятичных дробей столбиком выполняется в 2 шага:
1. Выполняем умножение столбиком, не обращая внимание на запятые.
2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе.
 Если в результате не хватает для этого цифр, дописываем слева нули.
Если в результате не хватает для этого цифр, дописываем слева нули.Разберем примеры таких расчетов на практике.
Пример 4Умножьте десятичные дроби 63,37 и 0,12 столбиком.
Решение
Первым делом выполним умножение чисел, игнорируя десятичные запятые.
Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 4. Дописывать нули не придется, т.к. знаков достаточно:
Ответ: 3,37·0,12=7,6044.
Пример 5Подсчитайте, сколько будет 3,2601 умножить на 0,0254.
Решение
Считаем без учета запятых. Получаем следующее число:
Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:
Ответ: 3,2601·0,0254=0,08280654.

Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д
Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:
Определение 2Если мы умножим десятичную дробь на 0,1, 0,01 и т.д., в итоге получится число, похожее на исходную дробь, запятая которого перенесена влево на нужное количество знаков. При нехватке цифр для переноса нужно дописывать нули слева.
Так, для умножения 45,34 на 0,1 надо перенести в исходной десятичной дроби запятую на один знак. У нас получится в итоге 4,534.
Пример 6Умножьте 9,4 на 0,0001.
Решение
Нам придется переносить запятую на четыре знака по количеству нулей во втором множителе, но цифр в первом для этого не хватит. Приписываем необходимые нули и получаем, что 9,4·0,0001=0,00094.
Ответ: 0,00094.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеДля бесконечных десятичных дробей мы пользуемся тем же правилом.
 Так, к примеру, 0,(18)·0,01=0,00(18) или 94,938…·0,1=9,4938…. и др.
Так, к примеру, 0,(18)·0,01=0,00(18) или 94,938…·0,1=9,4938…. и др.Как перемножить десятичную дробь с натуральным числом
Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.
Пример 7Подсчитайте, сколько будет 15·2,27.
Решение
Умножим столбиком исходные числа и отделим два знака запятой.
Ответ: 15·2,27=34,05.
Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.
Пример 8Вычислите произведение 0,(42) и 22.
Решение
Приведем периодическую дробь к виду обыкновенной.
0,(42)=0,42+0,0042+0,000042+…=0,421-0,01=0,420,99=4299=1433
Далее умножаем:
0,42·22=1433·22=14·223=283=913
Итоговый результат можем записать в виде периодической десятичной дроби как 9,(3).

Ответ: 0,(42)·22=9,(3).
Бесконечные дроби перед подсчетами надо предварительно округлить.
Пример 9Вычислите, сколько будет 4·2,145….
Решение
Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:
4·2,145…≈4·2,15=8,60.
Ответ: 4·2,145…≈8,60.
Как умножить десятичную дробь на 1000, 100, 10 и др
Умножение десятичной дроби на 10, 100 и др. часто встречается в задачах, поэтому мы разберем этот случай отдельно. Основное правило умножения звучит так:
Определение 3Чтобы умножить десятичную дробь на 1000, 100, 10 и др., нужно перенести ее запятую на 3, 2,1 цифры в зависимости от множителя и отбросить слева лишние нули. Если цифр для переноса запятой недостаточно, дописываем справа столько нулей, сколько нам нужно.
Покажем на примере, как именно это делать.
Пример 10Выполните умножение 100 и 0,0783.

Решение
Для этого нам надо перенести в десятичной дроби запятую на 2 цифры в правую сторону. Мы получим в итоге 007,83Нули, стоящие слева, можно отбросить и записать результат как 7,38.
Ответ: 0,0783·100=7,83.
Пример 11Умножьте 0,02 на 10 тысяч.
Решение: мы будем переносить запятую на четыре цифры вправо. В исходной десятичной дроби нам не хватит для этого знаков, поэтому придется дописывать нули. В этом случае будет достаточно трех 0. В итоге получилось 0,02000,перенесем запятую и получим 00200,0. Игнорируя нули слева, можем записать ответ как 200.
Ответ: 0,02·10 000=200.
Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.
Пример 12Вычислите произведение 5,32(672) на 1 000.
Решение: первым делом мы запишем периодическую дробь как 5,32672672672…, так вероятность ошибиться будет меньше.
 После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326,726726… Заключим период в скобки и запишем ответ как 5 326,(726).
После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326,726726… Заключим период в скобки и запишем ответ как 5 326,(726).Ответ: 5,32(672)·1 000=5 326,(726).
Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.
Как перемножить десятичную дробь с обыкновенной или со смешанным числом
Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.
Пример 13Умножьте 0,4 на 356
Решение
Cначала переведем десятичную дробь в обыкновенную. Имеем: 0,4=410=25.
Далее считаем: 0,4·356=25·236=2315=1815.
Мы получили ответ в виде смешанного числа. Можно записать его как периодическую дробь 1,5(3).
Ответ: 1,5(3).
Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.
Пример 14
Вычислите произведение 3,5678…·23
Решение
Второй множитель мы можем представить как 23=0,6666…. Далее округлим до тысячного разряда оба множителя. После этого нам будет нужно вычислить произведение двух конечных десятичных дробей 3,568 и 0,667. Посчитаем столбиком и получим ответ:
Итоговый результат нужно округлить до тысячных долей, так как именно до этого разряда мы округляли исходные числа. У нас получается, что 2,379856≈2,380.
Ответ: 3,5678…·23≈2,380
Калькулятор дробей
Ниже приведены несколько калькуляторов дробей, способных выполнять сложение, вычитание, умножение, деление, упрощение и преобразование дробей в десятичные дроби. Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.
Калькулятор смешанных чисел
Калькулятор упрощенных дробей
Калькулятор десятичных дробей
Калькулятор дробей в десятичную
Калькулятор дробей большого числа
Используйте этот калькулятор, если числители или знаменатели являются очень большими целыми числами.

В математике дробь — это число, которое представляет собой часть целого. Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих это целое. Например, в дроби
числитель равен 3, а знаменатель — 8. Более наглядный пример может включать пирог с 8 кусочками. 1 из этих 8 ломтиков будет составлять числитель дроби, а всего 8 ломтиков, составляющих весь пирог, будут знаменателем.Если бы человек съел 3 ломтика, оставшаяся часть пирога была бы такой, как показано на изображении справа. Обратите внимание, что знаменатель дроби не может быть равен 0, так как это сделает дробь неопределенной. Дроби могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.Дополнение:
В отличие от сложения и вычитания целых чисел, таких как 2 и 8, дроби требуют общего знаменателя для выполнения этих операций. Один из методов нахождения общего знаменателя заключается в умножении числителей и знаменателей всех участвующих дробей на произведение знаменателей каждой дроби.
 Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.Этот процесс можно использовать для любого количества фракций. Просто умножьте числители и знаменатели каждой дроби в задаче на произведение знаменателей всех остальных дробей (не включая соответствующий знаменатель) в задаче.
Альтернативный метод поиска общего знаменателя состоит в том, чтобы определить наименьшее общее кратное (НОК) для знаменателей, а затем сложить или вычесть числители, как если бы это было целое число. Использование наименьшего общего кратного может быть более эффективным и, скорее всего, приведет к дроби в упрощенной форме.
 В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное из этих трех чисел.
В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное из этих трех чисел.Кратное 2: 2, 4, 6, 8 10, 12 Кратное 4: 4, 8, 12 Кратное 6: 6, 12 Первое общее кратное — 12, так что это наименьшее общее кратное. Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители.
Вычитание:
Вычитание фракции по сути то же самое, что и сложение дроби. Для выполнения операции требуется общий знаменатель. Обратитесь к разделу добавления, а также к приведенным ниже уравнениям для пояснения.
Умножение:
Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат образует новый числитель и знаменатель.
 По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.Дивизион:
Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на величину, обратную дроби в знаменателе. Число, обратное числу , равно —
. Когда a является дробью, это, по сути, включает в себя замену числителя и знаменателя местами.Следовательно, величина, обратная дроби. Обратитесь к приведенным ниже уравнениям для пояснения.Упрощение:
Часто проще работать с упрощенными дробями. Таким образом, фракционные растворы обычно выражаются в их упрощенных формах.
, например, более громоздкий, чем. Предоставленный калькулятор возвращает входные дроби как в неправильной, так и в смешанной числовой форме. В обоих случаях дроби представлены в их низшей форме путем деления числителя и знаменателя на их наибольший общий множитель.Преобразование между дробями и десятичными знаками:
Преобразование десятичных дробей в дроби выполняется просто.
, что упрощается до, поскольку наибольший общий делитель между числителем и знаменателем равен 2. Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробьТочно так же дроби, знаменатели которых являются степенями 10 (или могут быть преобразованы в степени 10), могут быть переведены в десятичную форму, используя те же принципы. Возьмем, к примеру, дробь
. Чтобы преобразовать эту дробь в десятичную, сначала преобразуйте ее в дробь.Зная, что первый десятичный разряд представляет 10 -1 , можно преобразовать в 0,5. Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.
Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.Преобразование общей инженерной дроби в десятичную
В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже.
64 th 32 nd 16 th 8 th 4 th 2 nd Decimal Decimal
(дюйм к мм)1/64 0,015625 0,396875 2/64 1/32 0.03125 0,79375 3/64 0,046875 1,1 4/64 2/32 1/16 0,0625 1,5875 5/64 0,078125 1,984375 6/64 3/32 0.  09375
093752,38125 7/64 0,109375 2,778125 8/64 4/32 2/16 1/8 0,125 3,175 9/64 0,140625 3,571875 10/64 5/32 0.15625 3.96875 11/64 0,171875 4.365625 12/64 6/32 3/16 0,1875 4,7625 13/64 0,203125 5,159375 14/64 7/32 0.  21875
218755,55625 15/64 0,234375 5.953125 16/64 8/32 4/16 2/8 1/4 0,25 6,35 17/64 0,265625 6,746875 18/64 9/32 0.28125 7,14375 19/64 0,296875 7,540625 20/64 10/32 5/16 0,3125 7,9375 21/64 0,328125 8,334375 22/64 11/32 0.  34375
343758,73125 23/64 0,359375 9.128125 24/64 12/32 6/16 3/8 0,375 9,525 25/64 0,3 9,921875 26/64 13/32 0.40625 10,31875 27/64 0,421875 10,715625 28/64 14/32 7/16 0,4375 11,1125 29/64 0,453125 11,509375 30/64 15/32 0.  46875
4687511. 31/64 0,484375 12.303125 32/64 16/32 8/16 4/8 2/4 1/2 0,5 12,7 33/64 0,515625 13.096875 34/64 17/32 0.53125 13.49375 35/64 0,546875 13.8 36/64 18/32 9/16 0,5625 14,2875 37/64 0,578125 14,684375 38/64 19/32 0.  59375
5937515.08125 39/64 0.609375 15.478125 40/64 20/32 10/16 5/8 0,625 15,875 41/64 0,640625 16,271875 42/64 21/32 0.65625 16,66875 43/64 0,671875 17,065625 44/64 22/32 11/16 0,6875 17,4625 45/64 0,703125 17,859375 46/64 23/32 0.  71875
7187518,25625 47/64 0,734375 18,653125 48/64 24/32 12/16 6/8 3/4 0,75 19,05 49/64 0,765625 19,446875 50/64 25/32 0.78125 19.84375 51/64 0,796875 20.240625 52/64 26/32 13/16 0,8125 20,6375 53/64 0,828125 21,034375 54/64 27/32 0.  84375
8437521,43125 55/64 0,859375 21,828125 56/64 28/32 14/16 7/8 0,875 22,225 57/64 0,8 22,621875 58/64 29/32 0. 23,01875 59/64 0,921875 23,415625 60/64 30/32 15/16 0,9375 23,8125 61/64 0,953125 24,209375 62/64 31/32 0.  96875
9687524.60625 63/64 0,984375 25.003125 64/64 32/32 16/16 8/8 4/4 2/2 1 25,4 Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями в сочетании с целыми числами, десятичными знаками и смешанными числами.Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, т. Е. 1/2: 3 .Десятичные числа (десятичные числа) вводятся с десятичной запятой . , и они автоматически переводятся в дроби — i.е. 1,45 .
Двоеточие : и косая черта / являются символом деления. Может использоваться для деления смешанных чисел 1 2/3: 4 3/8 или может использоваться для записи сложных дробей, например 1/2: 1/3 .
Звездочка * или × — это символ умножения.
Плюс + — сложение, знак минус — — вычитание и () [] — математические скобки.
Символ возведения в степень / степени: ^ — например: (7 / 8-4 / 5) ^ 2 = (7 / 8-4 / 5) 2Примеры:
• сложение дробей: 2 / 4 + 3/4
• вычитание дробей: 2/3 — 1/2
• умножение дробей: 7/8 * 3/9
• деление дробей: 1/2: 3/4
• возведение дроби в степень: 3 / 5 ^ 3
• дробные показатели: 16 ^ 1/2
• сложение дробей и смешанные числа: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное в дробное: 0. 625
625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.Задачи с дробями:
следующие задачи по математике »
Что такое 2/4 из 4? (Вычислите 2/4 из 4)
В этой статье мы покажем вам, как именно вычислить 2/4 из 4, чтобы вы могли быстро и легко вычислить дробную часть любого числа! Приступим к математике!
Хотите быстро узнать или показать студентам, как конвертировать 2/4 из 4? Воспроизведите это очень быстрое и веселое видео прямо сейчас!
Вы, наверное, знаете, что число над чертой дроби называется числителем, а число под ним — знаменателем.Чтобы вычислить дробь любого числа, нам сначала нужно преобразовать это целое число в дробь.
Вот вам небольшой совет. Любое число можно преобразовать в дробь, если в качестве знаменателя использовать 1:
4 / 1
Итак, теперь, когда мы преобразовали 4 в дробь, чтобы получить ответ, мы помещаем дробь 2/4 рядом с нашей новой дробью, 4/1, чтобы мы могли умножить эти две дроби.

Правильно, все, что вам нужно сделать, это преобразовать целое число в дробь, а затем умножить числители и знаменатели.Давайте посмотрим:
2 х 4 / 4 х 1 знак равно 8 / 4
В этом случае нашу новую дробь можно еще больше упростить. Для этого нам нужно найти наибольший общий делитель обоих чисел.
Вы можете использовать наш удобный калькулятор GCF, чтобы вычислить это самостоятельно, если хотите. Мы уже сделали это, и GCF 8 и 4 составляет 4 .
Теперь мы можем разделить и новый числитель, и знаменатель на 4, чтобы упростить эту дробь до ее наименьших членов.
8/4 = 2
4/4 = 1
Когда мы сложим это вместе, мы увидим, что наш полный ответ:
2 / 1
Полный и упрощенный ответ на вопрос, что составляет 2/4 из 4:
2
Надеюсь, это руководство помогло вам понять, как найти дробную часть любого целого числа. Теперь вы можете попробовать больше чисел, чтобы попрактиковаться в новых навыках дробления.

Цитируйте, ссылайтесь или ссылайтесь на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.Мы очень ценим вашу поддержку!
«Что такое 2/4 из 4?». VisualFractions.com . По состоянию на 17 июля 2021 г. https://visualfractions.com/calculator/fraction-of-number/what-is-2-4-of-4/.
«Что такое 2/4 из 4?». VisualFractions.com , https://visualfractions.com/calculator/fraction-of-number/what-is-2-4-of-4/.Доступ 17 июля 2021 г.
Что такое 2/4 из 4 ?. VisualFractions.com. Получено с https://visualfractions.com/calculator/fraction-of-number/what-is-2-4-of-4/.
Калькулятор дробей числа
Дробь числа
Введите числитель, знаменатель и целое число
Вычисление следующей дроби числа
Что такое 2/4 из 2? (Вычислите 2/4 из 2)
В этой статье мы покажем вам, как именно вычислить 2/4 из 2, чтобы вы могли быстро и легко вычислить дробную часть любого числа! Приступим к математике!
Хотите быстро узнать или показать студентам, как преобразовать 2/4 из 2? Воспроизведите это очень быстрое и веселое видео прямо сейчас!
Вы, наверное, знаете, что число над чертой дроби называется числителем, а число под ним — знаменателем.
 Чтобы вычислить дробь любого числа, нам сначала нужно преобразовать это целое число в дробь.
Чтобы вычислить дробь любого числа, нам сначала нужно преобразовать это целое число в дробь.Вот вам небольшой совет. Любое число можно преобразовать в дробь, если в качестве знаменателя использовать 1:
2 / 1
Итак, теперь, когда мы преобразовали 2 в дробь, чтобы получить ответ, мы помещаем дробь 2/4 рядом с нашей новой дробью 2/1, чтобы мы могли умножить эти две дроби.
Правильно, все, что вам нужно сделать, это преобразовать целое число в дробь, а затем умножить числители и знаменатели.Давайте посмотрим:
2 х 2 / 4 х 1 знак равно 4 / 4
В этом случае нашу новую дробь можно еще больше упростить. Для этого нам нужно найти наибольший общий делитель обоих чисел.
Вы можете использовать наш удобный калькулятор GCF, чтобы вычислить это самостоятельно, если хотите. Мы уже сделали это, и GCF 4 и 4 составляет 4 .
Теперь мы можем разделить и новый числитель, и знаменатель на 4, чтобы упростить эту дробь до ее наименьших членов.

4/4 = 1
4/4 = 1
Когда мы сложим это вместе, мы увидим, что наш полный ответ:
1 / 1
Полный и упрощенный ответ на вопрос, что составляет 2/4 из 2:
1
Надеюсь, это руководство помогло вам понять, как найти дробную часть любого целого числа. Теперь вы можете попробовать больше чисел, чтобы попрактиковаться в новых навыках дробления.
Цитируйте, ссылайтесь или ссылайтесь на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.Мы очень ценим вашу поддержку!
«Что такое 2/4 из 2?». VisualFractions.com . По состоянию на 17 июля 2021 г. https://visualfractions.
 com/calculator/fraction-of-number/what-is-2-4-of-2/.
com/calculator/fraction-of-number/what-is-2-4-of-2/.«Что такое 2/4 из 2?». VisualFractions.com , https://visualfractions.com/calculator/fraction-of-number/what-is-2-4-of-2/.Доступ 17 июля 2021 г.
Что такое 2/4 из 2 ?. VisualFractions.com. Получено с https://visualfractions.com/calculator/fraction-of-number/what-is-2-4-of-2/.
Калькулятор дробей числа
Дробь числа
Введите числитель, знаменатель и целое число
Вычисление следующей дроби числа
Калькулятор фракций| Калькулятор дробей Меню
Калькулятор дробей
Дроби используются во всех формах математики.Калькуляторы в этом меню помогут вам узнать о дробях, как использовать дроби, и будут иметь дроби при их вычислении или в своем ответе.
Калькулятор сложения дробей — Узнайте, как складывать дроби
Калькулятор десятичных дробей — преобразование десятичных чисел в дробные
Калькулятор деления дробей — узнайте, как делить дроби
Калькулятор дробей в десятичную — преобразование дробей в десятичную форму
Калькулятор дробей в проценты — преобразование дробей в проценты
Калькулятор наибольшего общего множителя — Найдите наибольший общий делитель или делитель
Калькулятор умножения дробей — Узнайте, как умножать дроби
Калькулятор процентов в дробь — Преобразование процента в дробь
Упростите калькулятор дробей — приведите дроби к их простейшей форме
Калькулятор вычитания дробей — Узнайте, как вычитать дроби
Дроби могут быть неприятной частью математических задач.
 Они могут быть особенно неприятными, если вы не усвоите основы дробей до того, как начнете работать над более сложными задачами дробей. Знание того, как соотносить дроби с общим знаменателем, путем нахождения наибольшего общего множителя , очень важно освоить, прежде чем работать над сложными задачами дробей.
Они могут быть особенно неприятными, если вы не усвоите основы дробей до того, как начнете работать над более сложными задачами дробей. Знание того, как соотносить дроби с общим знаменателем, путем нахождения наибольшего общего множителя , очень важно освоить, прежде чем работать над сложными задачами дробей.Если проблема с дробями звучит как слишком знакомая проблема, калькулятор дробей может помочь вам вовремя и в отчаянии. С помощью CalcuNation.com мы предоставляем базовые калькуляторы дробей и более сложные онлайн-калькуляторы, которые используют дроби для вычисления ответа.
Наиболее распространенные способы использования калькулятора дробей
Приходилось ли вам складывать или вычитать дроби при работе с длинами? Как подрядчики построят дом правильно, не зная, как добавить 1/16 дюйма к 1/2 дюйма? Как насчет готовки? Как часто вам нужно корректировать рецепты, чтобы узнать, как приготовить половину порции, а не целую? Чтобы найти ответы на эти вопросы, необходимо иметь легкий доступ.Вместо того, чтобы полагаться на стандартный калькулятор, используйте калькулятор дробей , который у нас есть.
Чтобы использовать калькулятор дробей , выберите нужный тип из списка. После того, как вы нажмете на онлайн-калькулятор дробей по вашему выбору, заполните предоставленные поля. Информация, которую вам нужно предоставить, четко обозначена. Например, большинство перечисленных выше калькуляторов попросят вас указать число в числителе и число в знаменателе.Просто заполните необходимую информацию и произведите расчет. Это оно!
Наши онлайн-калькуляторы — отличный ресурс для расчета формул, поэтому добавьте эту страницу в закладки сегодня.
Просмотрите калькуляторы дробей, чтобы найти онлайн-калькулятор дробей , который поможет с вашими математическими задачами, связанными с процентами.Калькулятор дробей
Дополнительная информация
Существует четыре различных типа дробей: обыкновенные дроби, десятичные дроби, проценты и отношения.Когда слово «дробь» используется само по себе, обычно имеется в виду обычная дробь. И в этом смысле он использован здесь.
Обычная дробь записывается в виде двух целых чисел, расположенных одно над другим, разделенных короткой горизонтальной чертой. Нижнее число НЕ ДОЛЖНО быть нулевым.
Они также известны как вульгарные фракции .
Здесь дроби записываются по строкам, например, 3/4 .
Числитель — это первое число дроби.(N и P выше)
Знаменатель — это нижнее число дроби. (D и Q выше)
Итак, в 3/4 числитель равен 3 , а знаменатель — 4.
В правильной дроби числитель на меньше знаменателя.
В неправильной дроби числитель на больше, чем на знаменатель.
Итак, 3/4 — правильная дробь, а 4/3 — неправильная дробь.
Смешанное число состоит из двух частей: целого числа, за которым следует правильная дробь.
Эквивалентные дроби — это две или более дроби, которые имеют одинаковое значение, но различаются по форме. Все они имеют одинаковое значение, но выглядят по-разному
3/4 6/8 63/84 75% 0 . 75
Это эквивалентные дроби Имеется отдельная таблица эквивалентных дробей .
Дроби могут быть отрицательными, но в этом калькуляторе нельзя вводить отрицательные значения.
Кроме того, чтобы избежать отрицательного ответа при вычитании, первая дробь (слева) ДОЛЖНА быть больше второй дроби.
Если вам нужно, чтобы меньшее число было первым. : выполните вычисления, поместив сначала большее число, а затем поставьте знак минус перед ответом.
Например, чтобы сделать 1/5 — 2/3
do 2/3 — 1/5 , чтобы получить 7/15
и прочитать ответ как — 7 / 15Восстановленная фракция — это обычная фракция в ее простейшей возможной форме.
Чтобы получить это, верхнее и нижнее числа дроби делятся на ОДИНАКОВОЕ ЧИСЛО, и это повторяется при необходимости до тех пор, пока это становится невозможно.
Например, чтобы уменьшить 150/240
, сначала разделите оба на 2 , чтобы получить 75/120
, разделите оба на 3, чтобы получить 25/40
, затем разделите оба на 5, чтобы получите 5/8
и дальнейшее сокращение невозможно
В калькуляторе ответ всегда дается в сокращенном виде.Эквивалентные дроби — объяснения и примеры
В математике эквивалентные дроби — это просто дроби с разными числителями и знаменателями, но представляющие одну и ту же пропорцию целого. Эквивалентные дроби на первый взгляд кажутся разными, но имеют одинаковое или равное значение.
Например, эквивалентные дроби для 1/4:
2/8, 3/12, 4/16 и т. Д.
Эквивалентные дроби имеют одинаковое количество или значение после упрощения их числителя и знаменатели.Дроби будут генерировать одно и то же значение, если сокращение с использованием общего множителя производится как для числителя, так и для знаменателя.
Что такое эквивалентные дроби?Эквивалентные дроби — это две или более дроби, которые после упрощения дают одно и то же значение. Предположим, что a / b и c / d — две дроби, тогда дроби эквивалентны, только если упрощение каждой дроби приводит к e / f.
Другими словами,
a / b = c / d = e / f.
Например, дробь 1/3 имеет эквивалент 5/15, поскольку упрощение 5/15 приводит к тому же значению, что и 1/3.
Теперь возникает вопрос, почему эти дроби равны, несмотря на разные числа. Ответ на этот вопрос заключается в том, что дроби содержат числители и знаменатели, которые не являются совпадающими простыми числами. Следовательно, у них есть общее кратное, которое при делении дает одно и то же значение.
Давайте возьмем пример:
1/2 = 2/4 = 4/8
Вы можете заметить, что все же указанные выше две фракции имеют разные целые числа, но после деления числителя и знаменателя на общий множитель результат составляет:
(4 ÷ 4) / (8 ÷ 4)
= 1/2
В этом случае, если мы упростим 2/4, результат снова 1/2.
(2 ÷ 2) / (4 ÷ 2)
= 1/2
Было показано, что деление знаменателя или умножение числителя на один и тот же множитель не меняет значения дроби. И поэтому эквивалентные дроби при упрощении имеют одинаковую ценность.
Как найти эквивалентные дроби?Рассмотрим случай с дробью 1/5.
Умножение числителя и знаменателя на 2, 3 и 4 дает:
1/5 x 2/2 = 2/10
1/5 x 3/3 = 3/15
1/5 x 4 / 4 = 4/20
Следовательно, можно сделать вывод, что:
1/5 = 2/10 = 3/15 = 4/20
Эквивалентная дробь может быть получена только путем умножения или деления на общий множитель.При сложении или вычитании дроби изменяется только значение дроби.
Пример 1:
Учитывая, что дроби 5/16 и x / 12 эквивалентны, вычислите значение x.
Решение
Учитывая, что:
5/16 = x / 12
x = (5 x 12) / 16
x = 60/16
x = 15/4
Таким образом, значение x составляет 15/4.
Пример 2:
Найдите значение x, если дроби 3/5 и 4 / x эквивалентны.
Решение
Учитывая, что
3/5 = 4 / x
x = (4 x 5) / 3
x = 20/3
Практические вопросы
1. Запишите до 5 эквивалентные дроби для каждого из следующих:
(i) 3/4
(ii) 4/5
(iii) 6/7
(iv) 4/5
2. Найдите эквивалентные дроби имеющий знаменатель 12 для каждой из следующих дробей.
(i) 1/2(ii) 1/3
(iii) 3/4
(iv) 5/6
3.Замените следующие дроби на эквивалентные дроби со значением 24 в качестве знаменателя:
(i) 6/12(ii) 3/8
(iii) 2/6
(iv) 4/6
4. Определите пары дробей, которые эквивалентны и которые не являются:
(i) 2/3 и 8/12(ii) 3/7 и 12/28
(iii) 5/8 и 15/27
(iv) 36/44 и 9/11
(v) 4/5 и 5/4
(vi) 5/8 и 27/18
5.Я думаю о дроби, эквивалентной 10/15 с 2 в качестве числителя. О какой дроби с числителем 2 я думаю?
6. Эрик замечает, что 3/5 или 3/4 равно дроби 12/20. Какая дробь равна 12/20?
7. Джеймс отдает своему брату 2/5 ее коллекции орехов. Подсчитайте, сколько 1/5 своей коллекции орехов он отдает своему брату?
8. Питер дал 1/4 и 3/12 апельсина Дональду и Педро соответственно.Определите, выдал ли он эквивалентную долю апельсина.
9. Джон провел опрос в своем классе и обнаружил, что 56/96 учащихся, включенных в выборку, занимались спортом после школы. Выразить дробь в простейшей форме?
10. 7 — простое число в дробной части 7 / x. Каким числом можно заменить x в этой дроби, чтобы она не была в простейшей форме?
Предыдущий урок | Главная страница | Следующий урок .

 Поэтому получаем $0,75=\frac{75}{100}=\frac{3\cdot 25}{4\cdot 25}=\frac{3}{4}$ — вот и весь ответ.:)
Поэтому получаем $0,75=\frac{75}{100}=\frac{3\cdot 25}{4\cdot 25}=\frac{3}{4}$ — вот и весь ответ.:) {3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ. Она легко преобразуется:
Она легко преобразуется: Так или иначе, ключевое слово — «тысячных», т.е. 1000.
Так или иначе, ключевое слово — «тысячных», т.е. 1000.

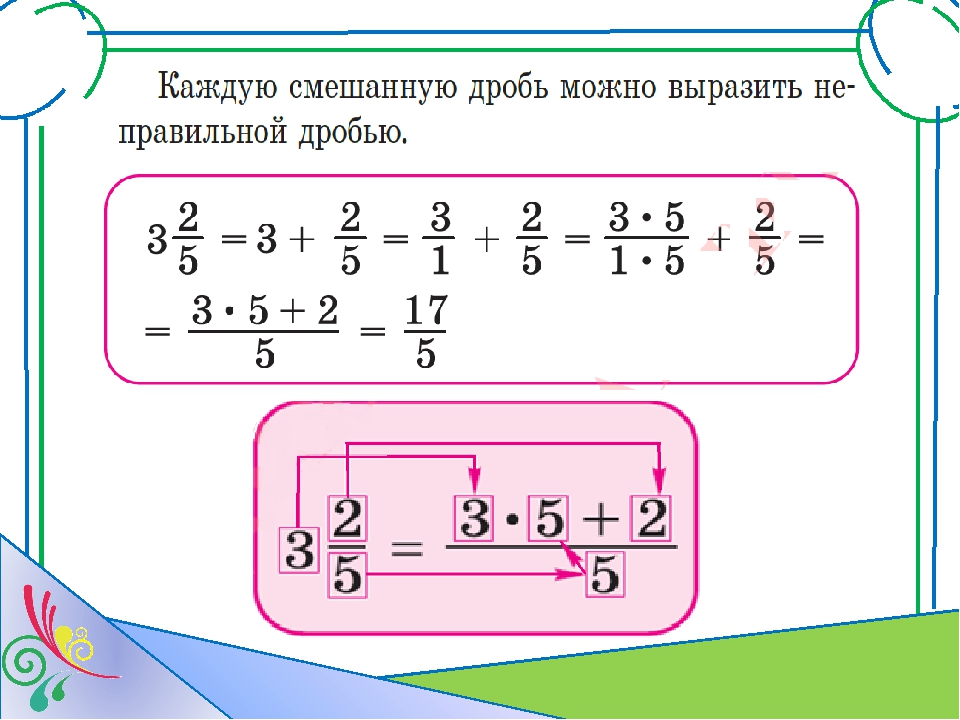





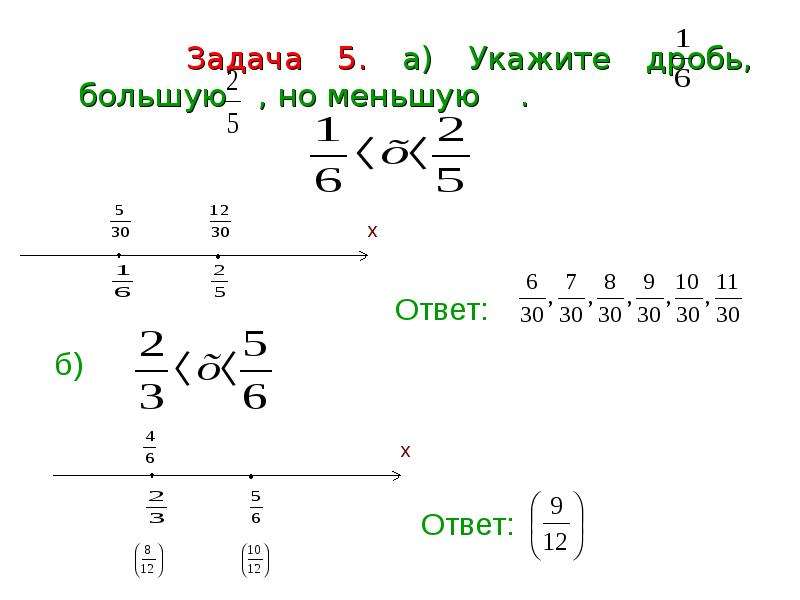
 д.
д. Наглядная табличка — наш друг-помощник:
Наглядная табличка — наш друг-помощник: Перевести 4,005 в смешанное число.
Перевести 4,005 в смешанное число. Например:
Например:





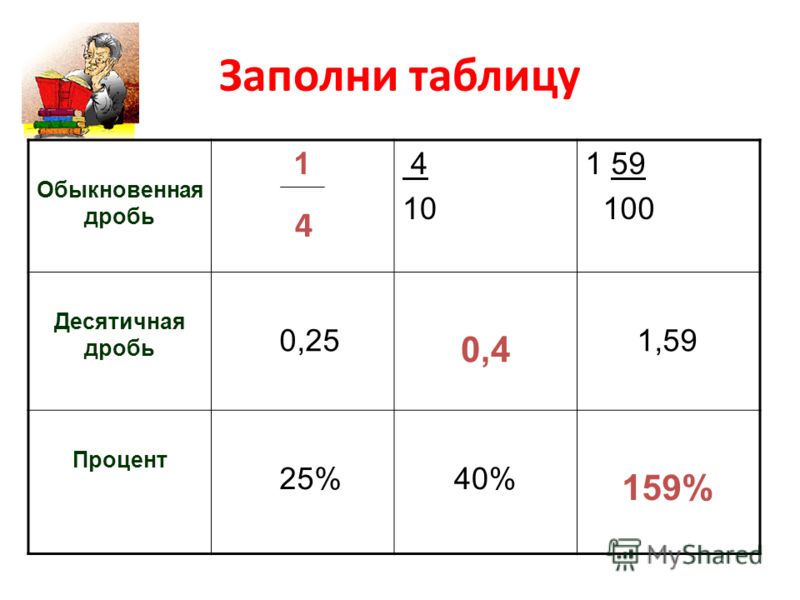
 Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.
Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение. Дробь состоит из числителя и знаменателя.
Дробь состоит из числителя и знаменателя. Как записать такую дробь?
Как записать такую дробь?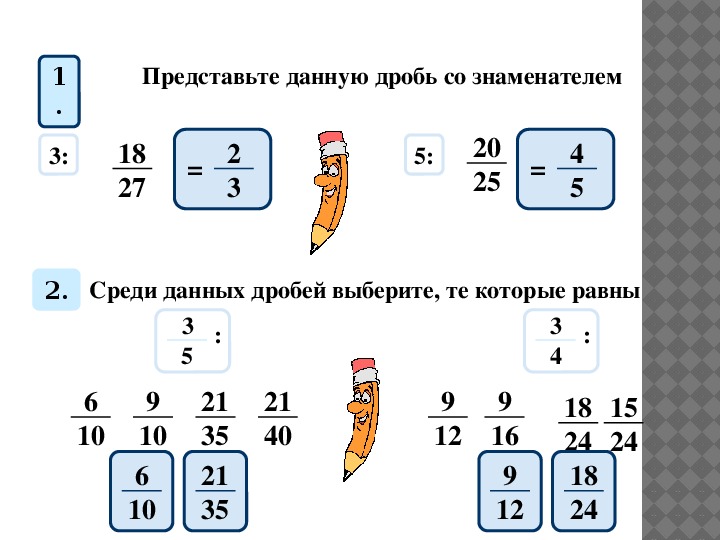

 Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.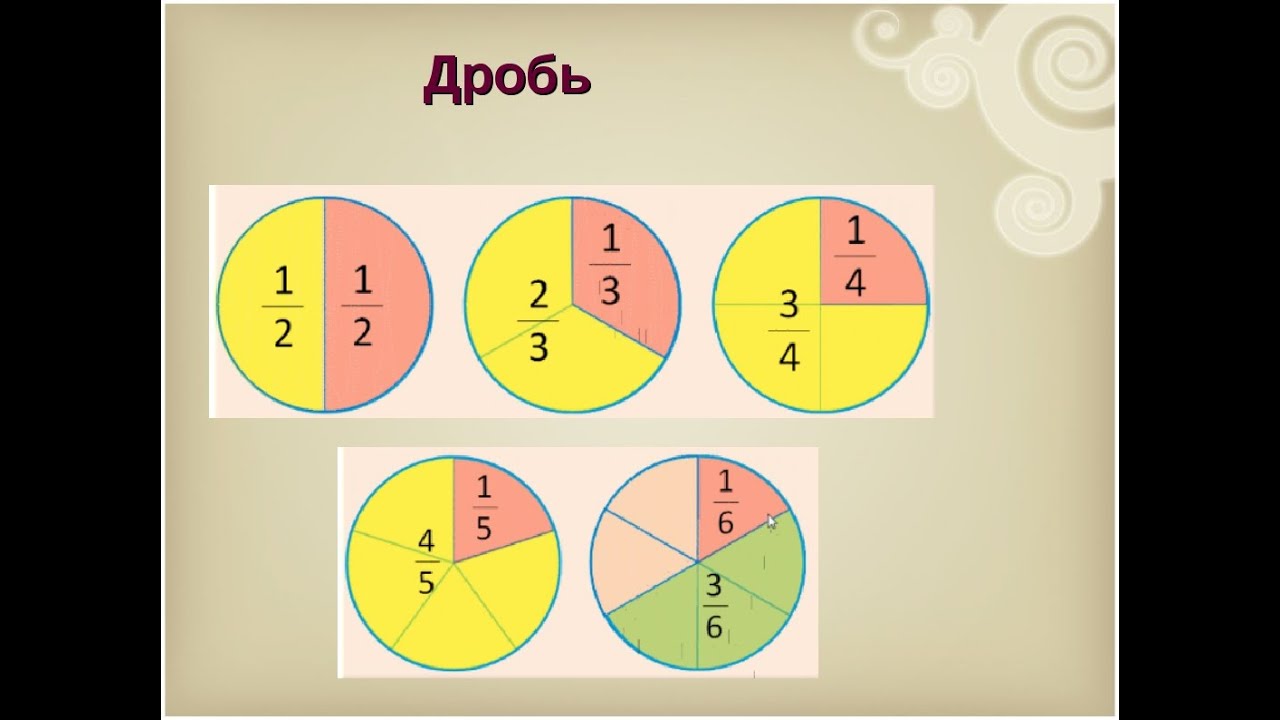 Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.
Чтобы хорошо понять, как это делается, рассмотрим пример из жизни. Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.
Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.
В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.
 Умножим её числитель и знаменатель на одно и то же число, например на число 2
Умножим её числитель и знаменатель на одно и то же число, например на число 2 Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы: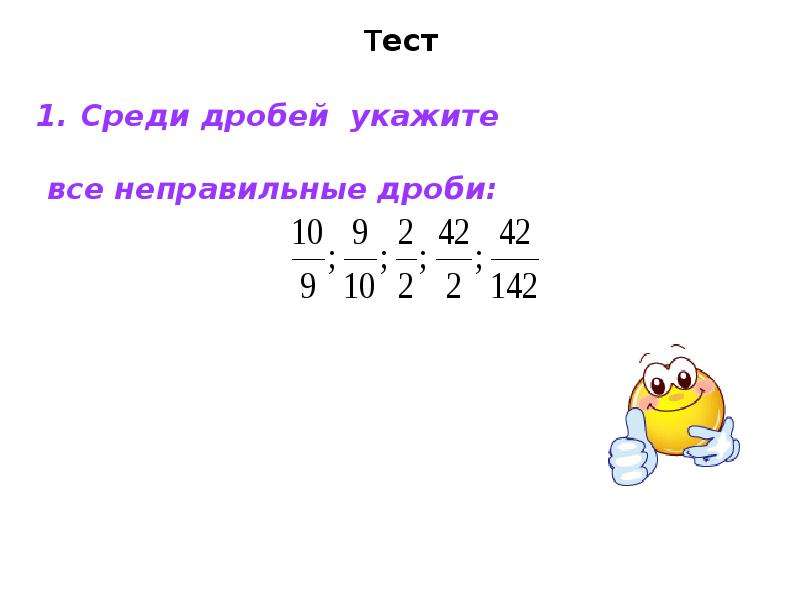 Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь .
Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь . А это действие, как было указано ранее, не меняет значение дроби.
А это действие, как было указано ранее, не меняет значение дроби.
 Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.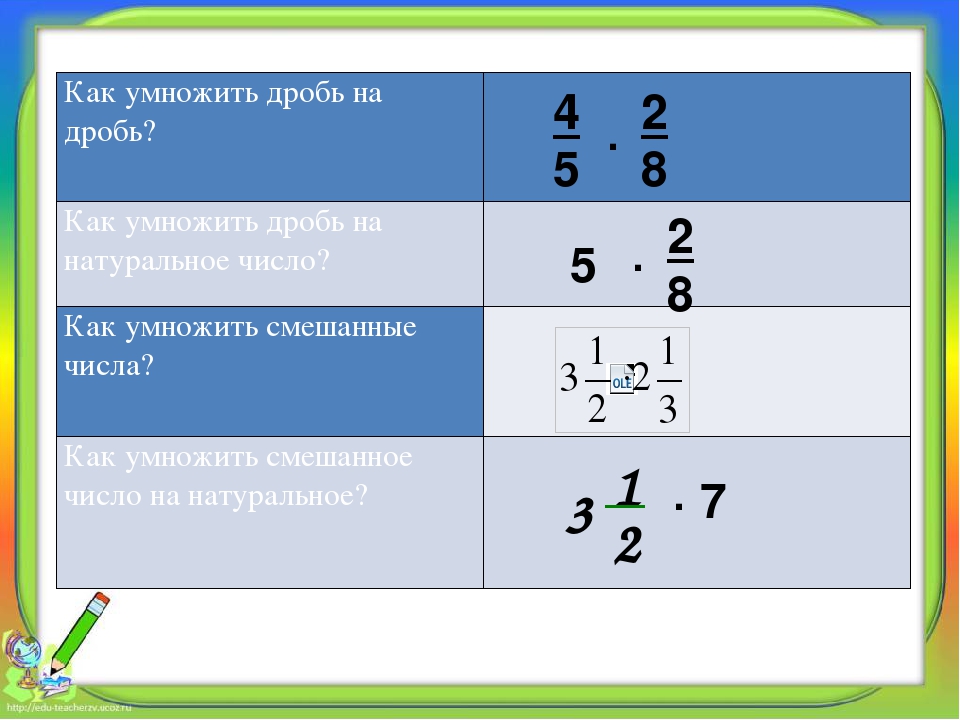
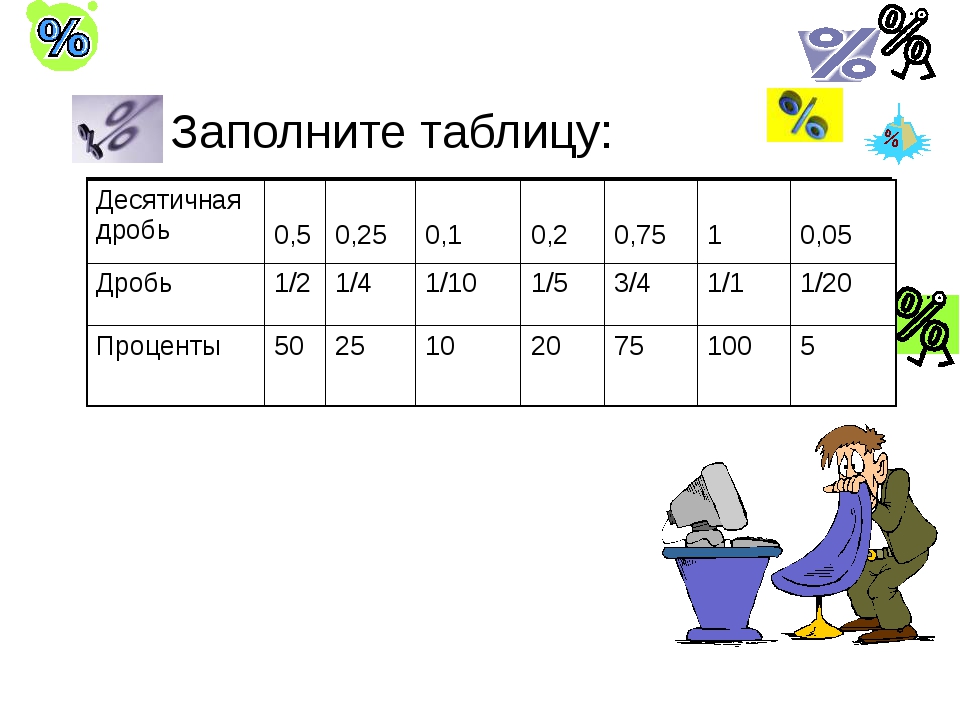 Запишите в виде дроби следующий рисунок:
Запишите в виде дроби следующий рисунок: Сократите следующие дроби вторым способом:
Сократите следующие дроби вторым способом: Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100, 10 и др.)
Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100, 10 и др.)
 статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.
статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример. Если в результате не хватает для этого цифр, дописываем слева нули.
Если в результате не хватает для этого цифр, дописываем слева нули.
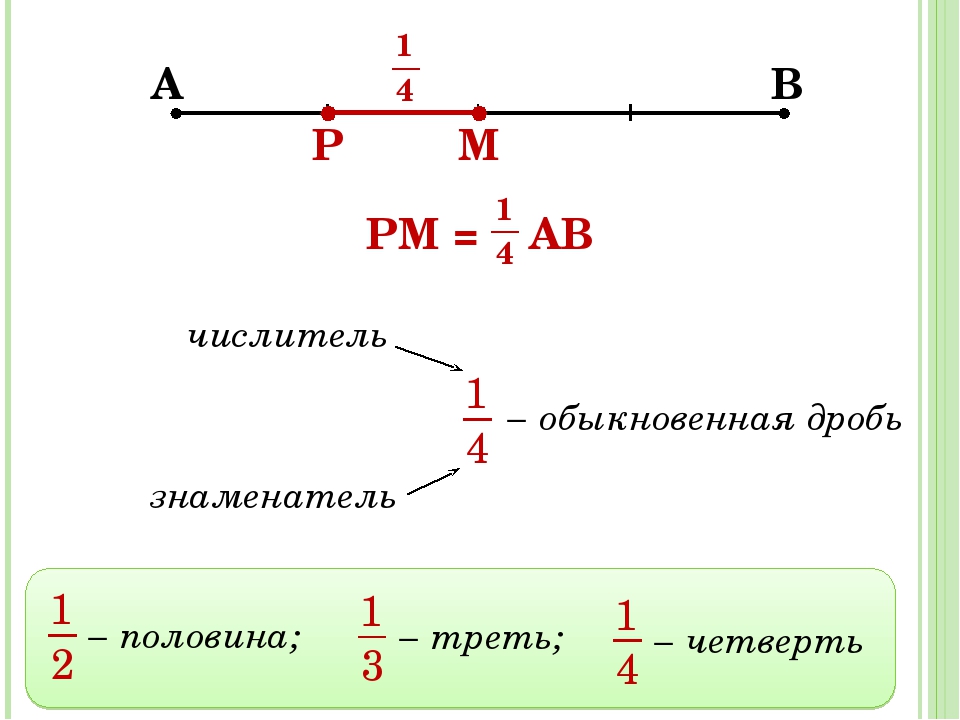 Так, к примеру, 0,(18)·0,01=0,00(18) или 94,938…·0,1=9,4938…. и др.
Так, к примеру, 0,(18)·0,01=0,00(18) или 94,938…·0,1=9,4938…. и др.

 После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326,726726… Заключим период в скобки и запишем ответ как 5 326,(726).
После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326,726726… Заключим период в скобки и запишем ответ как 5 326,(726).

 Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода. В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное из этих трех чисел.
В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное из этих трех чисел. По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения. Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.
Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик. 09375
09375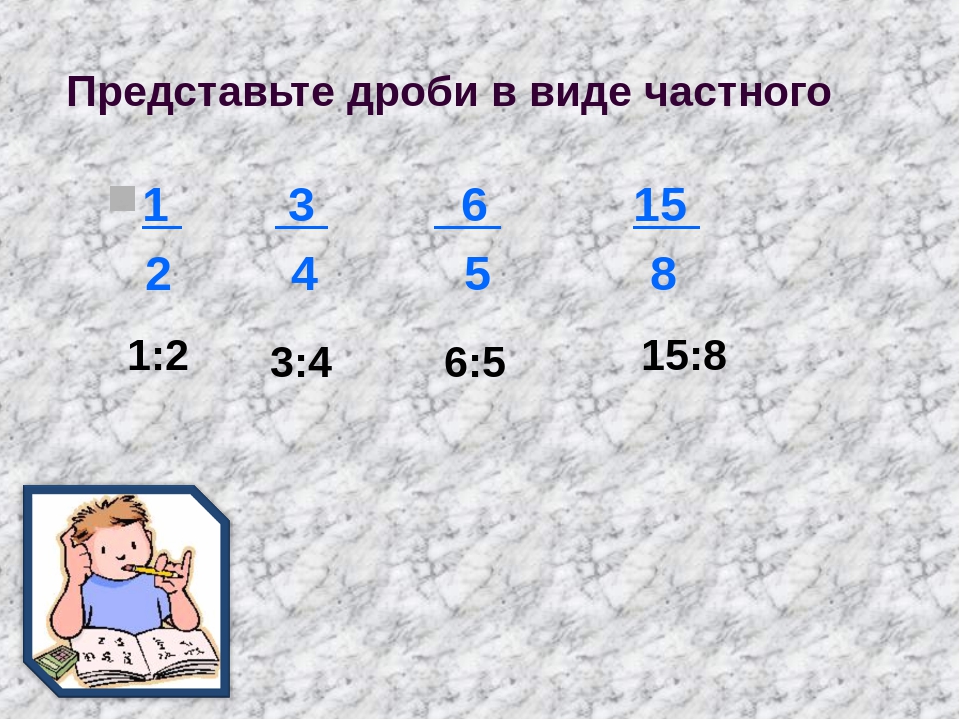 21875
21875 34375
34375 46875
46875 59375
59375 71875
71875 84375
84375 96875
96875
 625
625 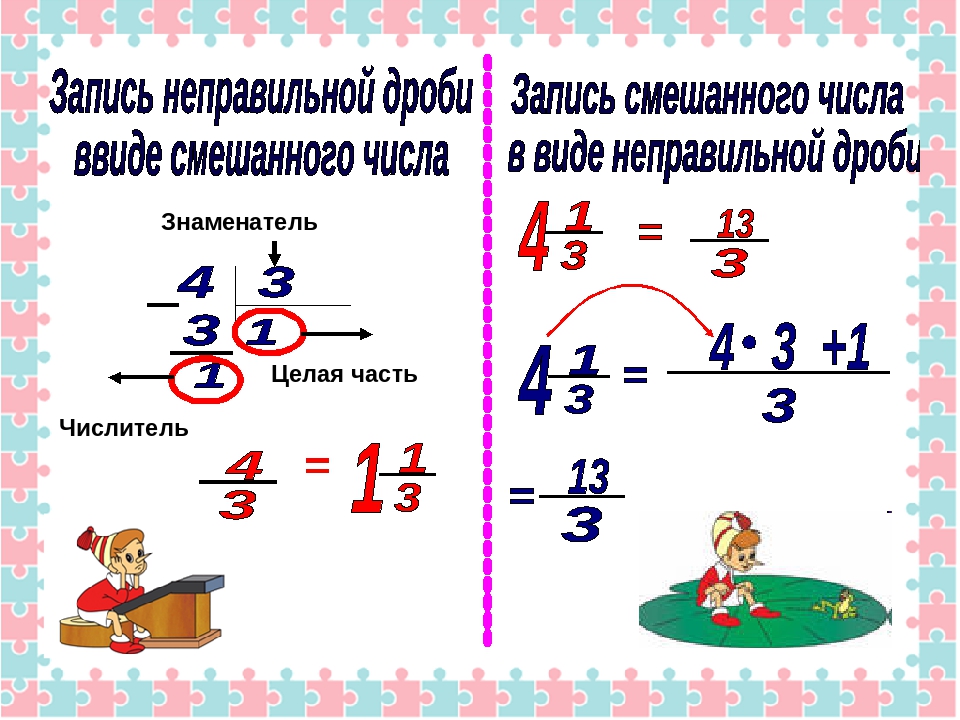
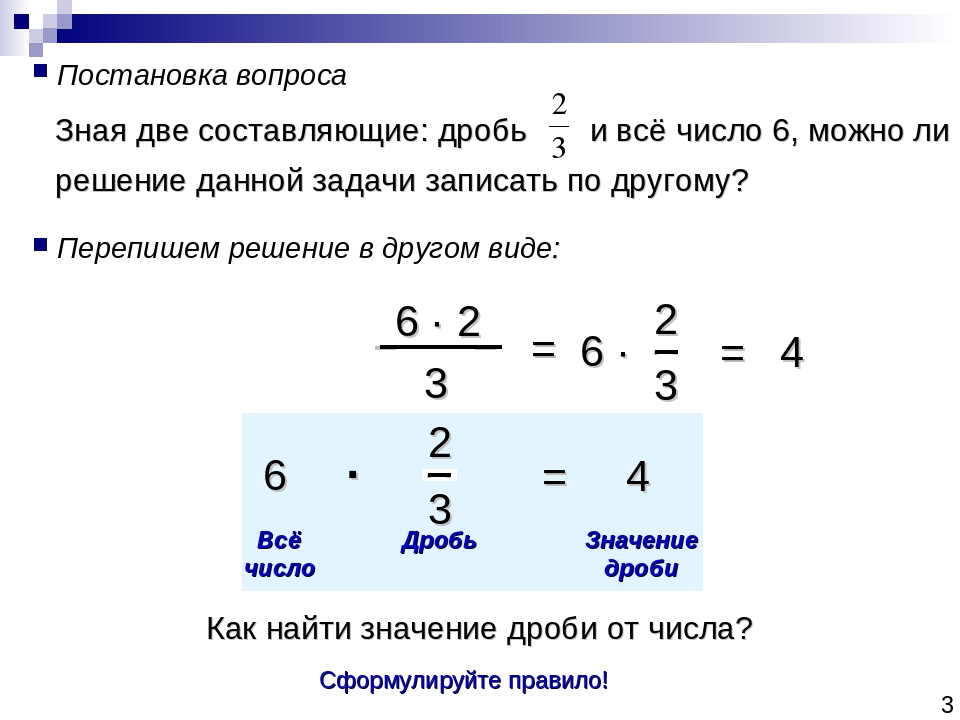

 Чтобы вычислить дробь любого числа, нам сначала нужно преобразовать это целое число в дробь.
Чтобы вычислить дробь любого числа, нам сначала нужно преобразовать это целое число в дробь.
 com/calculator/fraction-of-number/what-is-2-4-of-2/.
com/calculator/fraction-of-number/what-is-2-4-of-2/. Они могут быть особенно неприятными, если вы не усвоите основы дробей до того, как начнете работать над более сложными задачами дробей. Знание того, как соотносить дроби с общим знаменателем, путем нахождения наибольшего общего множителя , очень важно освоить, прежде чем работать над сложными задачами дробей.
Они могут быть особенно неприятными, если вы не усвоите основы дробей до того, как начнете работать над более сложными задачами дробей. Знание того, как соотносить дроби с общим знаменателем, путем нахождения наибольшего общего множителя , очень важно освоить, прежде чем работать над сложными задачами дробей.