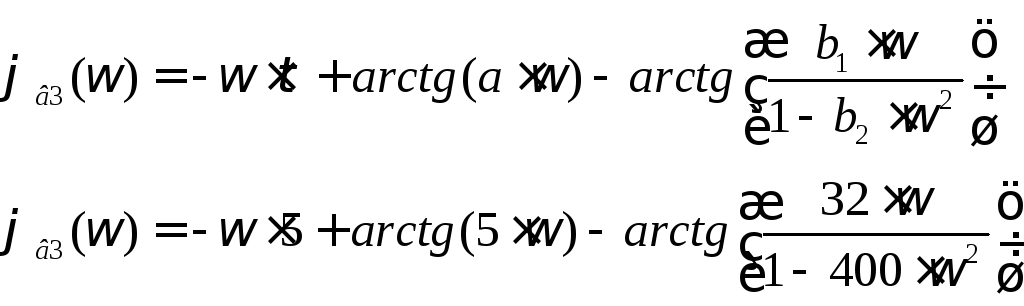Значение arctg 1 3. Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс? можно познакомиться с функциями и производными
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ:
рис. 1 – 4, рис. 2 — 1.
2 — 1.В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.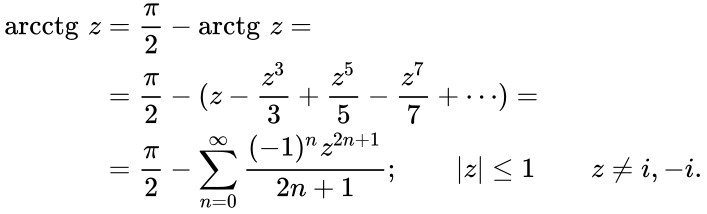
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот.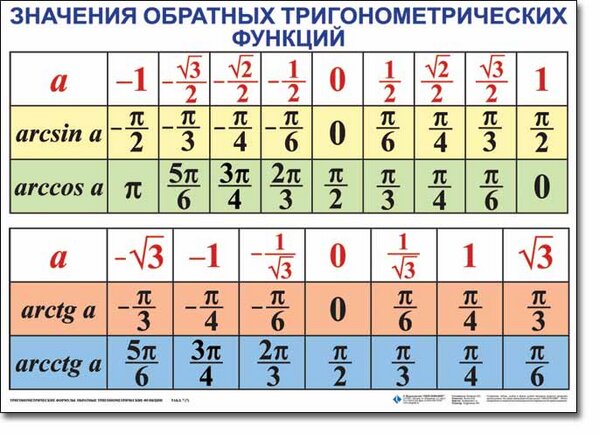 Знание подобных тождеств бывает полезным при решении конкретных примеров.
Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Арктангенс (y = arctg x )
— это функция, обратная к тангенсу (x = tg ytg(arctg x) = x
arctg(tg x) = x
Арктангенс обозначается так:
.
График функции арктангенс
График функции y = arctg x
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Арккотангенс, arcctg
Арккотангенс (y = arcctg
x
) — это функция, обратная к котангенсу (x = ctg
y
). Он имеет область определения и множество значений .
Он имеет область определения и множество значений .
ctg(arcctg
x)
= x
arcctg(ctg
x)
= x
Арккотангенс обозначается так:
.
График функции арккотангенс
График функции y = arcctg x
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(-
x)
=
arctg(-tg arctg
x)
=
arctg(tg(-arctg
x))
=
— arctg
x
Функция арккотангенс не является четной или нечетной:
arcctg(-
x)
=
arcctg(-ctg arcctg
x)
=
arcctg(ctg(π-arcctg
x))
=
π — arcctg
x ≠ ± arcctg
x
.
Свойства — экстремумы, возрастание, убывание
Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x
.
(см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
| — | π | |
| 0 |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.
| x | arctg x | arcctg x | ||
град. | рад. | град. | рад. | |
| — ∞ | — 90° | 180° | π | |
| — | — 60° | — | 150° | |
| — 1 | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | 0 | |
≈ 0,5773502691896258
≈ 1,7320508075688772
Формулы
Формулы суммы и разности
при
при
при
при
при
при
Выражения через логарифм, комплексные числа
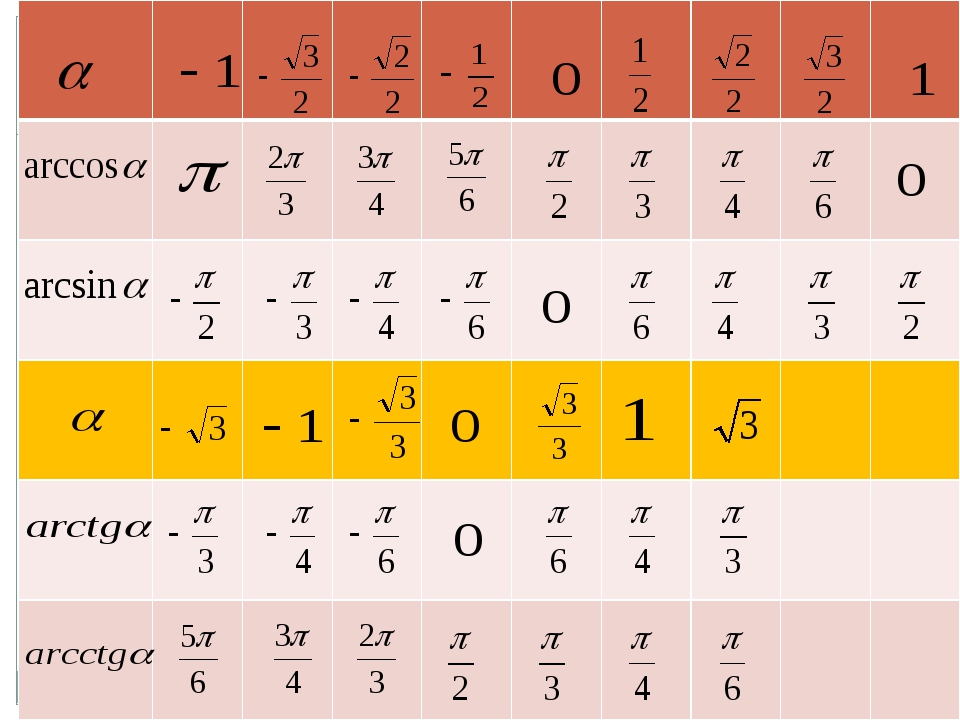
,
.
Выражения через гиперболические функции
Производные
См. Вывод производных арктангенса и арккотангенса > > >
Производные высших порядков :
Пусть .
Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.
См. Вывод производных высших порядков арктангенса и арккотангенса > > >
Там же даны формулы производных первых пяти порядков.
Аналогично для арккотангенса. Пусть .
Тогда
;
.
Интегралы
Делаем подстановку x = tg
t
и интегрируем по частям:
;
;
;
Выразим арккотангенс через арктангенс:
.
Разложение в степенной ряд
При |x| ≤ 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс , соответственно.
Следующие формулы справедливы на всей области определения:
tg(arctg
x)
= x
ctg(arcctg
x)
= x
.
Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg
x)
= x
при
arcctg(ctg
x)
= x
при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс.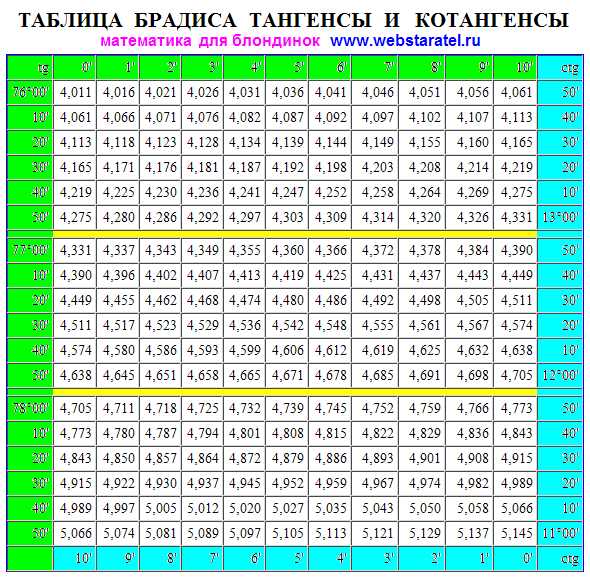 Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится. ) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите. ) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1.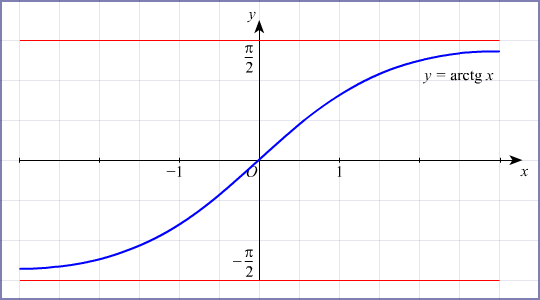 Это будет 2.) Что и является правильным ответом.
Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y
-1 ≤
x ≤ 1 и множество значений -π/2 ≤
y ≤ π/2 .
sin(arcsin
x)
= x
arcsin(sin
x)
= x
Арксинус иногда обозначают так:
.
График функции арксинус
График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арксинуса.
Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
). Он имеет область определения -1 ≤
x ≤ 1 и множество значений 0 ≤
y ≤ π
.
cos(arccos
x)
= x
arccos(cos
x)
= x
Арккосинус иногда обозначают так:
.
График функции арккосинус
График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x
Функция арккосинус не является четной или нечетной:
arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x ≠ ± arccos
x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | — 1 ≤ x ≤ 1 | — 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
град. | рад. | град. | рад. | |
| — 1 | — 90° | — | 180° | π |
| — | — 60° | — | 150° | |
| — | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
Выражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков :
,
где — многочлен степени .
Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin
t
.
Интегрируем по частям, учитывая что -π/2
≤ t ≤ π/2 ,
cos
t ≥ 0 :
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| 1 имеет место следующее разложение:
;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус , соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin
x)
= x
cos(arccos
x)
= x
.
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin
x)
= x
при
arccos(cos
x)
= x
при .
Использованная литература:
И.Н. Бронштейн, К. А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса ».
Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты.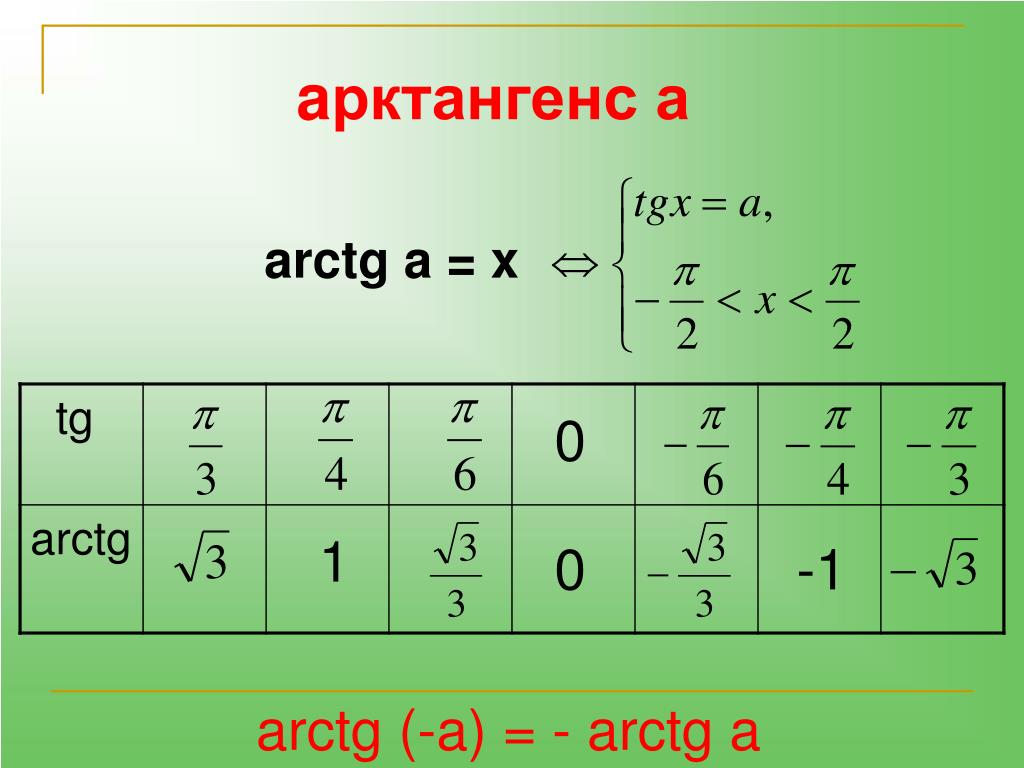 Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a
, arccos(−a)=π−arccos a
, arctg(−a)=−arctg a
и arcctg(−a)=π−arcctg a
.
Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a
, arccos(−a)=π−arccos a
, arctg(−a)=−arctg a
и arcctg(−a)=π−arcctg a
.
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса. Будем это делать на примерах.
Пусть нам требуется найти значение арксинуса 0,2857
. Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже). Ему соответствует синус 16
градусов 36
минут. Следовательно, искомым значением арксинуса числа 0,2857
является угол 16
градусов 36
минут.
Часто приходится учитывать и поправки из трех справа столбцов таблицы. К примеру, если нам нужно найти арксинус 0,2863
. По таблице синусов это значение получается как 0,2857
плюс поправка 0,0006
, то есть, значению 0,2863
соответствует синус 16
градусов 38
минут (16
градусов 36
минут плюс 2
минуты поправки).
Если же число, арксинус которого нас интересует, отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно отыскать два наиболее близких к нему значения синусов, между которыми данное число заключено. Например, мы ищем значение арксинуса числа 0,2861573
. Этого числа нет в таблице, с помощью поправок это число тоже не получить. Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.
 п.
п.Например, пусть нам известно, что arcsin a=−π/12 , а нужно найти значение arccos a . Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12 .
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Пусть нам известно, что арккосинус числа a равен π/10 , и нужно вычислить значение арктангенса этого числа a . Решить поставленную задачу можно так: по известному значению арккосинуса найти число a , после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.
Угол π/10
радиан – это угол 18
градусов, по таблице косинусов находим, что косинус 18
градусов приближенно равен 0,9511
, тогда число a
в нашем примере есть 0,9511
.
Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511
, оно приближенно равно 43
градусам 34
минутам.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg .
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.
 — 96 с.: ил. ISBN 5-7107-2667-2
— 96 с.: ил. ISBN 5-7107-2667-2
Где на окружности находится arctg 1 3. Арксинус, формула, график функции арксинус, урок и презентация
Ранее по программе учащиеся получили представление о решении тригонометрических уравнений, ознакомились с понятиями арккосинуса и арксинуса, примерами решений уравнений cos t = a и sin t = a. В этом видеоуроке рассмотрим решение уравнений tg x = a и ctg x = a.
В начале изучения данной темы рассмотрим уравнения tg x = 3 и tg x = — 3. Если уравнение tg x = 3 будем решать с помощью графика, то увидим, что пересечение графиков функций y = tg x и y = 3 имеет бесконечное множество решений, где x = x 1 + πk. Значение x 1 — это координата x точки пересечения графиков функций y = tg x и y = 3. Автор вводит понятие арктангенса: arctg 3 это число, tg которого равен 3, и это число принадлежит интервалу от -π/2 до π/2. Используя понятие арктангенса, решение уравнения tg x = 3 можно записать в виде x = arctg 3 + πk.
По аналогии решается уравнение tg x = — 3.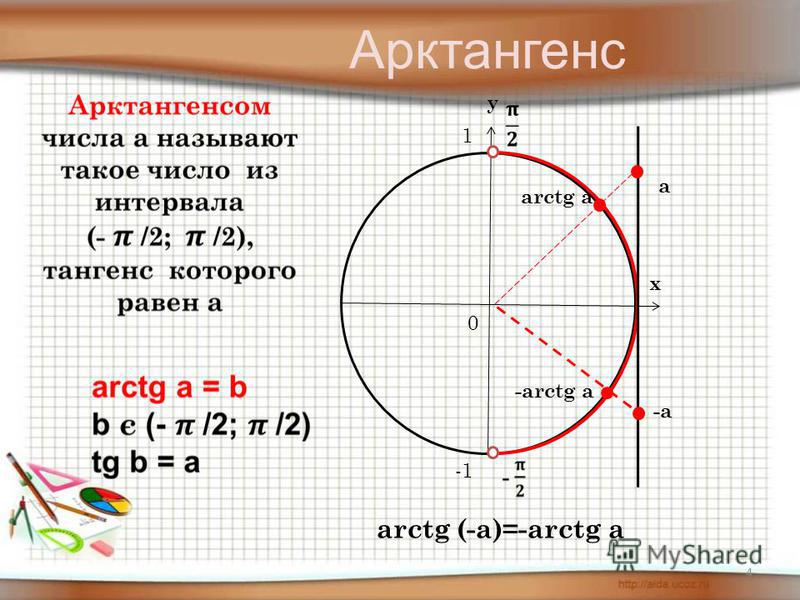 По построенным графикам функций y = tg x и y = — 3 видно, что точки пересечения графиков, а следовательно, и решениями уравнений, будет x = x 2 + πk. С помощью арктангенса решение можно записать как x = arctg (- 3) + πk. На следующем рисунке увидим, что arctg (- 3) = — arctg 3.
По построенным графикам функций y = tg x и y = — 3 видно, что точки пересечения графиков, а следовательно, и решениями уравнений, будет x = x 2 + πk. С помощью арктангенса решение можно записать как x = arctg (- 3) + πk. На следующем рисунке увидим, что arctg (- 3) = — arctg 3.
Общее определение арктангенса выглядит следующим образом: арктангенсом а называется такое число из промежутка от -π/2 до π/2, тангенс которого равен а. Тогда решением уравнения tg x = a является x = arctg a + πk.
Автор приводит пример 1. Найти решение выражения arctg.Введем обозначения: арктангенс числа равен x, тогда tg x будет равен данному числу, где x принадлежит отрезку от -π/2 до π/2. Как в примерах в предыдущих темах, воспользуемся таблицей значений. По этой таблице тангенсу данного числа соответствует значение x = π/3. Запишем решение уравнения арктангенс заданного числа равен π/3, π/3 принадлежит и интервалу от -π/2 до π/2.
Пример 2 — вычислить арктангенс отрицательного числа. Используя равенство arctg (- a) = — arctg a, введем значение x.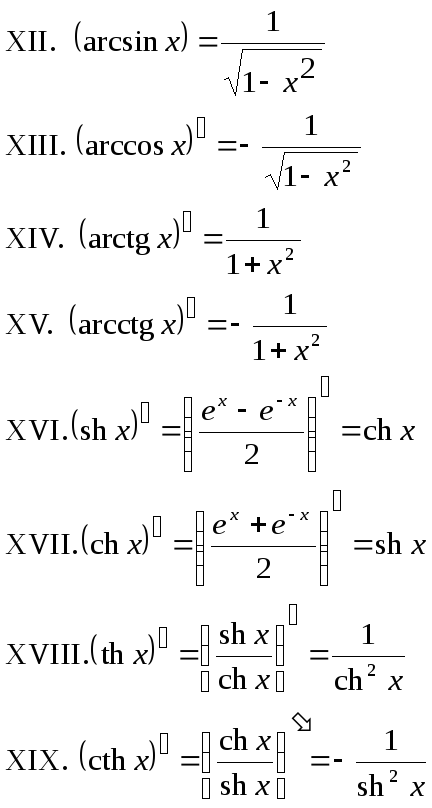 Аналогично примеру 2 запишем значение x, которое принадлежит отрезку от -π/2 до π/2. По таблице значений найдем, что x = π/3, следовательно, — tg x = — π/3. Ответом уравнения будет — π/3.
Аналогично примеру 2 запишем значение x, которое принадлежит отрезку от -π/2 до π/2. По таблице значений найдем, что x = π/3, следовательно, — tg x = — π/3. Ответом уравнения будет — π/3.
Рассмотрим пример 3. Решим уравнение tg x = 1. Запишем, что x = arctg 1 + πk. В таблице значению tg 1 соответствует значение x = π/4, следовательно, arctg 1 = π/4. Подставим это значение в исходную формулу x и запишем ответ x = π/4 + πk.
Пример 4: вычислить tg x = — 4,1. В данном случае x = arctg (- 4,1) + πk. Т.к. найти значение arctg в данном случае нет возможности, ответ будет выглядеть как x = arctg (- 4,1) + πk.
В примере 5 рассматривается решение неравенства tg x > 1. Для решения построим графики функций y = tg x и y = 1. Как видно на рисунке, эти графики пересекаются в точках x = π/4 + πk. Т.к. в данном случае tg x > 1, на графике выделим область тангенсоиды, которая находится выше графика y = 1, где x принадлежит интервалу от π/4 до π/2. Ответ запишем как π/4 + πk
Далее рассмотрим уравнение ctg x = a. На рисунке изображены графики функций у = ctg x, y = a, y = — a, которые имеют множество точек пересечения. Решения можно записать как x = x 1 + πk, где x 1 = arcctg a и x = x 2 + πk, где x 2 = arcctg (- a). Отмечено, что x 2 = π — x 1 . Из этого следует равенство arcctg (- a) = π — arcctg a. Далее дается определение арккотангенса: арккотангенсом а называется такое число из промежутка от 0 до π, котангенс которого равен а. Решение уравнения сtg x = a записывается в виде: x = arcctg a + πk.
На рисунке изображены графики функций у = ctg x, y = a, y = — a, которые имеют множество точек пересечения. Решения можно записать как x = x 1 + πk, где x 1 = arcctg a и x = x 2 + πk, где x 2 = arcctg (- a). Отмечено, что x 2 = π — x 1 . Из этого следует равенство arcctg (- a) = π — arcctg a. Далее дается определение арккотангенса: арккотангенсом а называется такое число из промежутка от 0 до π, котангенс которого равен а. Решение уравнения сtg x = a записывается в виде: x = arcctg a + πk.
В конце видеоурока делается еще один важный вывод — выражение ctg x = a можно записать в виде tg x = 1/a, при условии, что a не равно нулю.
ТЕКСТОВАЯ РАСШИФРОВКА:
Рассмотрим решение уравнений tg х = 3 и tg х= — 3. Решая первое уравнение графически, мы видим, что графики функций у = tg х и у = 3 имеют бесконечно много точек пересечения, абсциссы которых запишем в виде
х = х 1 + πk, где х 1 — это абсцисса точки пересечения прямой у = 3 с главной ветвью тангенсоиды (рис.1), для которой было придумано обозначение
arctg 3 (арктангенс трех).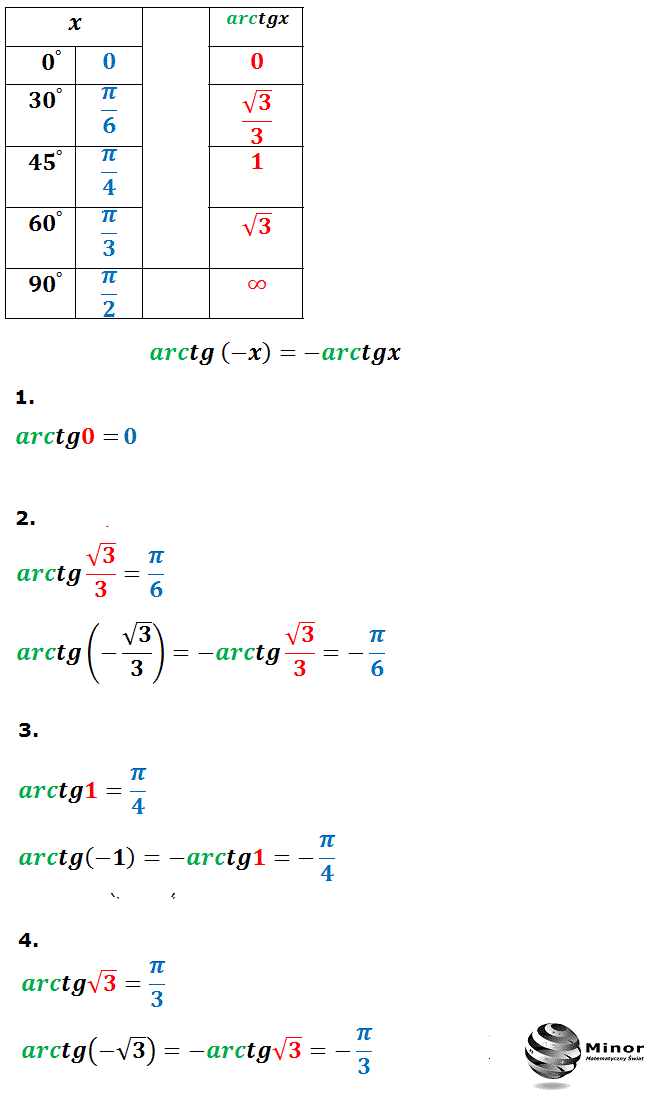
Как же понимать arctg 3?
Это число, тангенс которого равен 3 и это число принадлежит интервалу (- ;). Тогда все корни уравнения tg х = 3 можно записать формулой х = arctg 3+πk.
Аналогично решение уравнения tg х = — 3 можно записать в виде х = х 2 + πk, где х 2 — это абсцисса точки пересечения прямой у = — 3 с главной ветвью тангенсоиды (рис.1), для которой было придумано обозначение arctg(-3) (арктангенс минус трех). Тогда все корни уравнения можно записать формулой: х = arctg(-3)+ πk. По рисунку видно, что arctg(- 3)= — arctg 3.
Сформулируем определение арктангенса. Арктангенсом а называется такое число из промежутка (-;), тангенс которого равен а.
Часто используют равенство: arctg(-а) = -arctg а, которое справедливо для любого а.
Зная определение арктангенса, сделаем общий вывод о решении уравнения
tg х= a: уравнение tg х = a имеет решение х = arctg а + πk.
Рассмотрим примеры.
ПРИМЕР 1.Вычислить arctg.
Решение. Пусть arctg = х, тогда tgх = и хϵ (- ;). Показать таблицу значений Следовательно, х =, так как tg = и ϵ (- ;).
Пусть arctg = х, тогда tgх = и хϵ (- ;). Показать таблицу значений Следовательно, х =, так как tg = и ϵ (- ;).
Итак, arctg =.
ПРИМЕР 2. Вычислить arctg (-).
Решение. Используя равенство arctg(- а) = — arctg а, запишем:
arctg(-) = — arctg . Пусть — arctg = х, тогда — tgх = и хϵ (- ;). Следовательно, х =, так как tg = и ϵ (- ;). Показать таблицу значений
Значит — arctg=- tgх= — .
ПРИМЕР 3. Решить уравнение tgх = 1.
1. Запишем формулу решений: х = arctg 1 + πk.
2. Найдем значение арктангенса
так как tg = . Показать таблицу значений
Значит arctg1= .
3. Поставим найденное значение в формулу решений:
ПРИМЕР 4. Решить уравнение tgх = — 4,1(тангенс икс равно минус четыре целые одна десятая).
Решение. Запишем формулу решений: х = arctg (- 4,1) + πk.
Вычислить значение арктангенса мы не можем, поэтому решение уравнения оставим в полученном виде.
ПРИМЕР 5. Решить неравенство tgх 1.
Решение.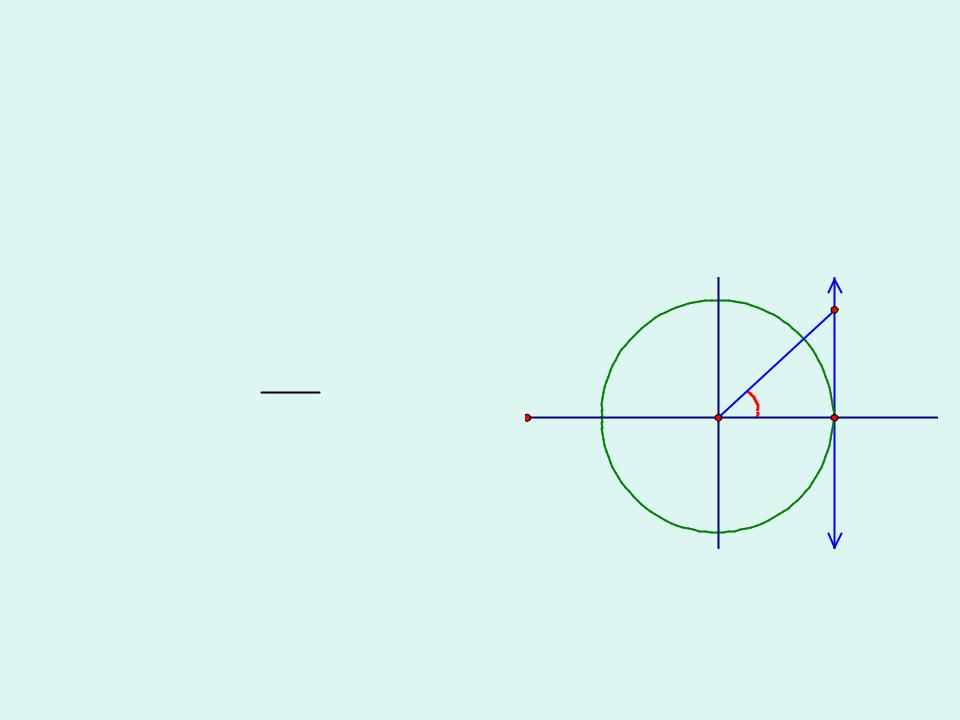 Будем решать графически.
Будем решать графически.
- Построим тангенсоиду
у= tgх и прямую у = 1(рис.2). Они пересекаются в точках вида х = + πk.
2. Выделим промежуток оси икс, на котором главная ветвь тангенсоиды расположена выше прямой у = 1, так как по условию tgх 1. Это интервал (;).
3. Используем периодичность функции.
Своийство 2. у=tg х — периодическая функция с основным периодом π.
Учитывая периодичность функции у= tgх, запишем ответ:
(;). Ответ можно записать в виде двойного неравенства:
Перейдем к уравнению ctg х = a. Представим графическую иллюстрацию решения уравнения для положительного и отрицательного а (рис.3).
Графики функций у= ctg х и у =а а также
у= ctg х и у=-а
имеют бесконечно много общих точек, абсциссы которых имеют вид:
х = х 1 + , где х 1 — это абсцисса точки пересечения прямой у =а с главной ветвью тангенсоиды и
х 1 = arcсtg а;
х = х 2 + , где х 2 — это абсцисса точки пересечения прямой
у = — а с главной ветвью тангенсоиды и х 2 = arcсtg (- а).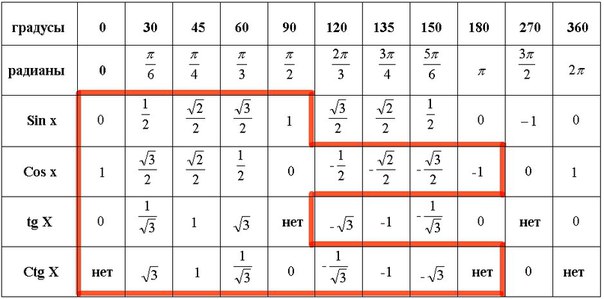
Заметим, что х 2 = π — х 1 . Значит, запишем важное равенство:
arcсtg (-а) = π — arcсtg а.
Сформулируем определение: арккотангенсом а называется такое число из интервала (0;π), котангенс которого равен а.
Решение уравнения ctg х = a записываются в виде: х = arcсtg а + .
Обратим внимание, что уравнение ctg х = a можно преобразовать к виду
tg х = , за исключение, когда а = 0.
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.
График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков».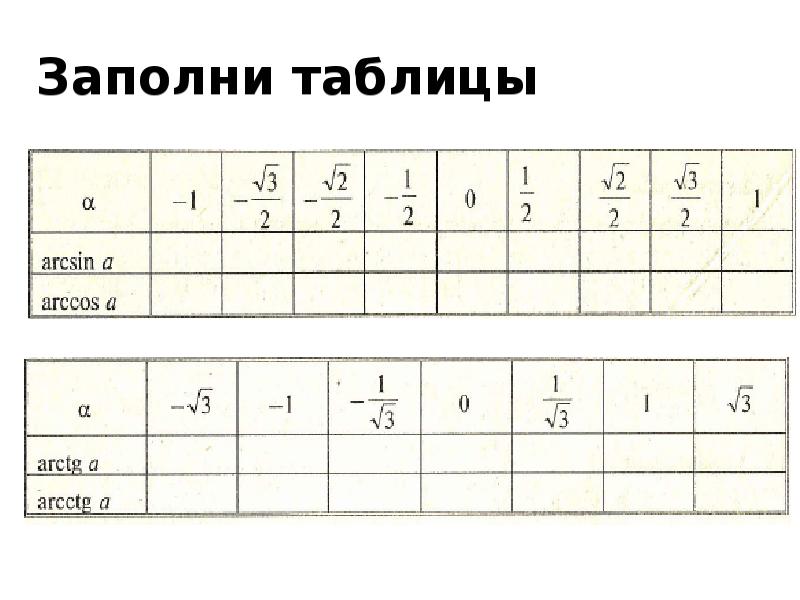 Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.

Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Чем больше формул помнит школьник, тем проще найти ответ задания.
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Эта статья про нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса данного числа. Сначала мы внесем ясность, что называется значением арксинуса, арккосинуса, арктангенса и арккотангенса. Дальше получим основные значения этих аркфункций, после чего разберемся, как находятся значения арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса. Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Наконец, поговорим про нахождение арксинуса числа, когда известен арккосинус, арктангенс или арккотангенс этого числа, и т.п.
Навигация по странице.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса ».
Таблицы синусов и косинусов, а также тангенсов и котангенсов Брадиса позволяют найти значение арксинуса, арккосинуса, арктангенса и арккотангенса положительного числа в градусах с точностью до одной минуты. Здесь стоит оговориться, что нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса отрицательных чисел можно свести к нахождению значений соответствующих аркфункций положительных чисел, обратившись к формулам arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(−a)=−arcsin a , arccos(−a)=π−arccos a , arctg(−a)=−arctg a и arcctg(−a)=π−arcctg a .
Разберемся с нахождением значений арксинуса, арккосинуса, арктангенса и арккотангенса по таблицам Брадиса.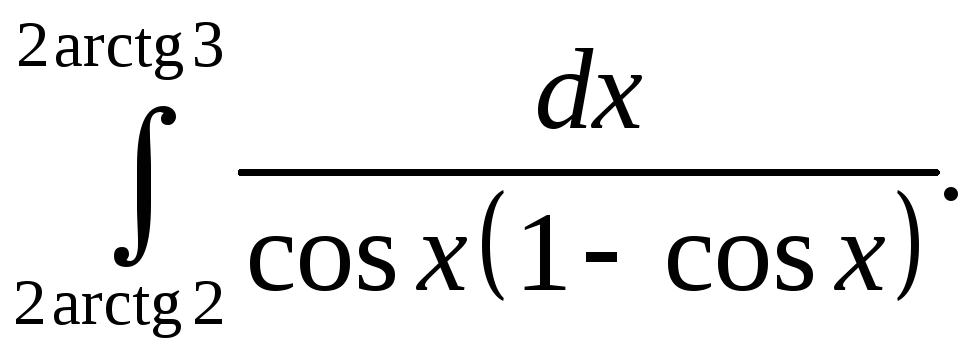 Будем это делать на примерах.
Будем это делать на примерах.
Пусть нам требуется найти значение арксинуса 0,2857
. Находим это значение в таблице синусов (случаи, когда это значение отсутствует в таблице, разберем ниже). Ему соответствует синус 16
градусов 36
минут. Следовательно, искомым значением арксинуса числа 0,2857
является угол 16
градусов 36
минут.
Часто приходится учитывать и поправки из трех справа столбцов таблицы. К примеру, если нам нужно найти арксинус 0,2863
. По таблице синусов это значение получается как 0,2857
плюс поправка 0,0006
, то есть, значению 0,2863
соответствует синус 16
градусов 38
минут (16
градусов 36
минут плюс 2
минуты поправки).
Если же число, арксинус которого нас интересует, отсутствует в таблице и даже не может быть получено с учетом поправок, то в таблице нужно отыскать два наиболее близких к нему значения синусов, между которыми данное число заключено. Например, мы ищем значение арксинуса числа 0,2861573
. Этого числа нет в таблице, с помощью поправок это число тоже не получить. Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Тогда находим два наиболее близких значения 0,2860
и 0,2863
, между которыми исходное число заключено, этим числам соответствуют синусы 16
градусов 37
минут и 16
градусов 38
минут. Искомое значение арксинуса 0,2861573
заключено между ними, то есть, любое из этих значений угла можно принять в качестве приближенного значения арксинуса с точностью до 1
минуты.
Абсолютно аналогично находятся и значения арккосинуса, и значения арктангенса и значения арккотангенса (при этом, конечно, используются таблицы косинусов, тангенсов и котангенсов соответственно).
Нахождение значения arcsin через arccos, arctg, arcctg и т.п.
Например, пусть нам известно, что arcsin a=−π/12 , а нужно найти значение arccos a . Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12 .
Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a
требуется найти значение арктангенса или арккотангенса этого числа a
или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.
Пусть нам известно, что арккосинус числа a равен π/10 , и нужно вычислить значение арктангенса этого числа a . Решить поставленную задачу можно так: по известному значению арккосинуса найти число a , после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.
Угол π/10
радиан – это угол 18
градусов, по таблице косинусов находим, что косинус 18
градусов приближенно равен 0,9511
, тогда число a
в нашем примере есть 0,9511
.
Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511
, оно приближенно равно 43
градусам 34
минутам.
Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg .
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н.
 Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7 - Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень.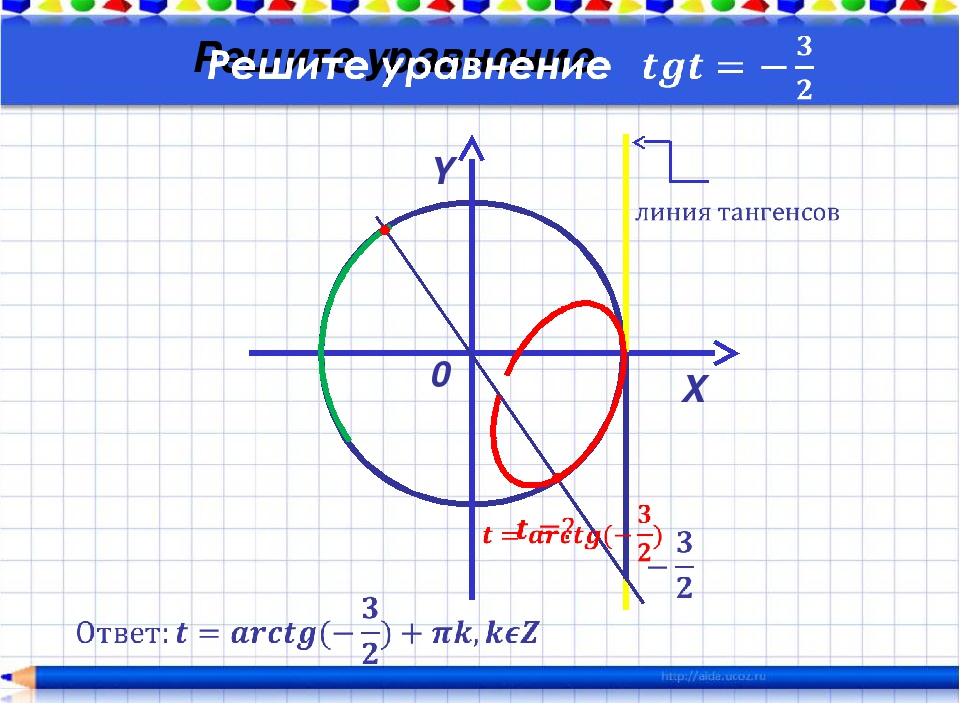 ..»
..»
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да. ..) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
..) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
3 arctg 0
Вы искали 3 arctg 0? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 4 arctg 1, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «3 arctg 0».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 3 arctg 0,4 arctg 1,4 арктангенс 1,6 arctg,arccos онлайн,arctg 0,arctg 0 1,arctg 0 2,arctg 0 25,arctg 0 3,arctg 0 4,arctg 0 5,arctg 0 6,arctg 0 arctg 1,arctg 0 равен,arctg 1 0,arctg 1 2 в градусах,arctg 1 4,arctg 1 5,arctg 1 6,arctg 1 arctg 0,arctg 1 в градусах,arctg 10,arctg 2 0,arctg 2 3 в градусах,arctg 2 5,arctg 2 в градусах,arctg 3 0,arctg 3 5,arctg 3 в градусах,arctg 4,arctg 4 1,arctg 4 3 в градусах,arctg 4 5,arctg 4 в градусах,arctg 5,arctg 5 2,arctg 5 3,arctg 5 4,arctg 6,arctg 7,arctg 8,arctg в градусах,arctg как вычислить,arctg как найти,arctg калькулятор,arctg калькулятор онлайн,arctg калькулятор онлайн в градусах,arctg онлайн,arctg онлайн калькулятор,arctg онлайн калькулятор в градусах,arctg таблица,arctg таблица значений,arctg4,online arctg,арккотангенс онлайн,арктангенс 0,арктангенс 0 1,арктангенс 0 25,арктангенс 0 4,арктангенс 0 5,арктангенс 0 75,арктангенс 0 чему равен,арктангенс 1 2,арктангенс 1 2 в градусах,арктангенс 1 3,арктангенс 1 3 в градусах,арктангенс 1 4,арктангенс 1 5,арктангенс 1 в градусах,арктангенс 1 в радианах,арктангенс 2 3,арктангенс 2 в градусах,арктангенс 3,арктангенс 3 2,арктангенс 3 4 в градусах,арктангенс 3 в градусах,арктангенс 4 в градусах,арктангенс 45,арктангенс 5,арктангенс 8,арктангенс в градусах,арктангенс в градусах калькулятор,арктангенс вычислить,арктангенс вычислить онлайн,арктангенс как вычислить,арктангенс как посчитать,арктангенс калькулятор,арктангенс калькулятор в градусах,арктангенс калькулятор онлайн,арктангенс калькулятор онлайн в градусах,арктангенс калькулятор онлайн в градусах и минутах,арктангенс на калькуляторе,арктангенс найти,арктангенс нуля,арктангенс онлайн,арктангенс онлайн калькулятор,арктангенс онлайн калькулятор в градусах,арктангенс онлайн калькулятор в градусах и минутах,арктангенс посчитать,арктангенс посчитать онлайн,арктангенс равен 1,арктангенс угла,арктангенс числа онлайн,арктангенсы таблица,вычисление арккосинуса онлайн,вычисление арктангенса,вычисление арктангенса онлайн,вычислить arctg онлайн калькулятор,вычислить арккосинус онлайн,вычислить арктангенс,вычислить арктангенс онлайн,инженерный онлайн калькулятор с арктангенсом,как вычислить arctg,как вычислить арктангенс,как найти арктангенс,как найти арктангенс числа,как посчитать арктангенс,как считать арктангенс,калькулятор arctg,калькулятор arctg онлайн,калькулятор arctg онлайн в градусах,калькулятор арккосинус в градусах онлайн,калькулятор арктангенс,калькулятор арктангенс в градусах,калькулятор арктангенса,калькулятор арктангенса онлайн,калькулятор арктангенсов,калькулятор арктангенсов в градусах онлайн,калькулятор арктангенсов онлайн,калькулятор арктангенсов онлайн в градусах,калькулятор онлайн arctg,калькулятор онлайн арктангенс,калькулятор онлайн арктангенс в градусах,калькулятор онлайн с арктангенсом,калькулятор онлайн с арктангенсом онлайн,калькулятор с арктангенсом,калькулятор с арктангенсом онлайн,на калькуляторе арктангенс,найти арктангенс,найти арктангенс онлайн,онлайн арктангенс числа,онлайн вычисление арктангенса,онлайн калькулятор arccos в градусах,онлайн калькулятор arctg,онлайн калькулятор arctg в градусах,онлайн калькулятор арктангенс,онлайн калькулятор арктангенса,онлайн калькулятор арктангенсов,онлайн калькулятор арктангенсов в градусах,онлайн калькулятор с арктангенсом,онлайн калькулятор с арктангенсом онлайн,онлайн расчет арктангенса,онлайн считать арктангенс,перевод арктангенса в градусы,перевод арктангенса в градусы онлайн,посчитать арккосинус онлайн,посчитать арктангенс,посчитать арктангенс в градусах онлайн,посчитать арктангенс онлайн,посчитать арктангенс онлайн в градусах,расчет арктангенса онлайн,таблица arctg,таблица арков,таблица брадиса arctg,таблица значений арктангенс,чему равен arctg,чему равен арктангенс 1. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 3 arctg 0. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 4 арктангенс 1).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 3 arctg 0. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 4 арктангенс 1).
Где можно решить любую задачу по математике, а так же 3 arctg 0 Онлайн?
Решить задачу 3 arctg 0 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Арксинус, арккосинус и арктангенс угла
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской.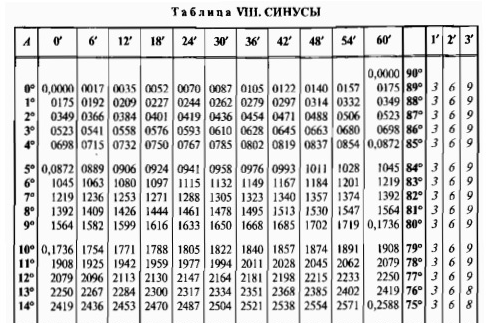 Не понимает он эти термины и, стало
быть, не доверяет этой славной семейке.) А зря. Это очень простые
понятия. Которые, между прочим, колоссально облегчают жизнь знающему
человеку при решении тригонометрических уравнений!
Не понимает он эти термины и, стало
быть, не доверяет этой славной семейке.) А зря. Это очень простые
понятия. Которые, между прочим, колоссально облегчают жизнь знающему
человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать
эпических ляпов.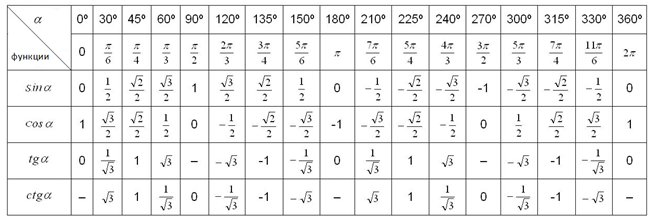 ) Например, выражение arccos1,8 выглядит вполне
солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
) Например, выражение arccos1,8 выглядит вполне
солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов. Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов. Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит заклинание: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё. .. Заменяем все арки на значения в радианах, всё
посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что
и является правильным ответом.
.. Заменяем все арки на значения в радианах, всё
посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что
и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
Те, кто освоил темы «Тригонометрический круг», и «Отсчёт углов на тригонометрическом круге» — люди грамотные. И, возможно, уже приготовили мне убойный вопрос.) По определению, скажем, arcsin 0,5 — это угол, синус которого равен 0,5. Т.е 30°. Но…
Грамотный человек знает, что синус равен 0,5 не только у угла 30°! Так как:
sin30° = 0,5
sin150° = 0,5
sin390° = 0,5
sin510° = 0,5
И так до бесконечности… Неоднозначно получается! Получается, что arcsin0,5 это и 30°, и 150°, и 390°, и 510°, и ….
Да. Именно так. Арксинус 0,5 — это действительно
бесконечный набор углов. Но обозначается такой арксинус вот как:
Arcsin0,5. С заглавной буквы. В школе такие арксинусы не изучают. В
школе изучают арки с маленькой буквы: arcsin, arccos, arctg, arcctg. Такие арки называются главными значениями арксинуса, арккосинуса и т.д. и
имеют жёсткие ограничения по величине. Для однозначности.
Такие арки называются главными значениями арксинуса, арккосинуса и т.д. и
имеют жёсткие ограничения по величине. Для однозначности.
С этими ограничениями надо разобраться основательно. Тем более, что это дело простое.) Запоминаем:
arсsin (любой) — это угол, который располагается в интервале:
arсcos (любой) — это угол, который располагается в интервале:
arсtg (любой) — это угол, который располагается в интервале:
arсctg (любой) — это угол, который располагается в интервале:
Запомнить эти диапазоны очень легко по картинкам. Тригонометрический круг вам в помощь!) Для арксинуса:
Зелёным нарисованы углы, которые пробегают значения от
— Пи/2 до + Пи/2. Это и есть разрешённая зона для арксинусов. И никаких
дополнительных оборотов! Строго от -90° до +90°! Никакой arcsin не может
быть равным, например 120°, 180° или 330°. А вот 50°, -65°, 90° или
25° — пожалуйста!
А вот 50°, -65°, 90° или
25° — пожалуйста!
Теперь, я думаю, понятно, что arcsin 0,5 = 30°. И только 30°! Так как углы 150°, 390°, 510° и т.д., которые тоже дают синус, равный 0,5, арксинусами быть не могут. Они выпадают из разрешённого диапазона.
А теперь наведите курсор мышки на рисунок. Вы увидите диапазон арктангенсов. Найдите 2 отличия.) Да! Конечные точки на оси ОУ стали белыми! Это означает, что они не включаются в диапазон арктангенсов. Арктангенс не может быть равным ±90°. По той простой причине, что тангенс 90° (и -90°) не существует.
Уже проще, правда?) Ну и, аналогичная картинка для арккосинуса и арккотангенса (при наведённом курсоре):
Надеюсь, зрительная память вас спасёт, если что…)
А зачем все эти арки? — слышу ещё один осторожный вопрос.)
Вопрос резонный. В математике просто так, чисто для красоты, ничего не бывает. Только по острой необходимости!) А вы попробуйте ответить на такой вопрос:
У какого угла синус равен 0,4?
Для ответа в градусах или радианах вам придётся открывать
таблицы Брадиса, или включать солидный калькулятор. Искать там значение
синуса, равное (примерно!) 0,4 и смотреть, какой же угол имеет этот
синус. После тяжких трудов вы определите, что это угол примерно 23 градуса и 36 минут. Про радианы я вообще молчу…)
Искать там значение
синуса, равное (примерно!) 0,4 и смотреть, какой же угол имеет этот
синус. После тяжких трудов вы определите, что это угол примерно 23 градуса и 36 минут. Про радианы я вообще молчу…)
А через арксинус мгновенно даётся абсолютно точный ответ: угол, у которого синус равен 0,4 — это arcsin 0,4 ! Просто по смыслу арксинуса: arcsin 0,4 — это и есть угол, синус которого равен 0,4. Разумеется, это не единственный угол, синус которого равен 0,4, но через арки и все остальные записываются в три секунды. Этим мы в тригонометрических уравнениях займёмся.
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a, тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.
Для четкого понимания рассмотрим пример.
Если имеем арккосинус угла равного π3, то значение косинуса отсюда равно 12 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 12 получим π на 3. Такое тригонометрическое выражение записывается как arcos(12)=π3.
Величиной угла может быть как градус, так и радиан. Значение угла π3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 12 имеет значение 60 градусов.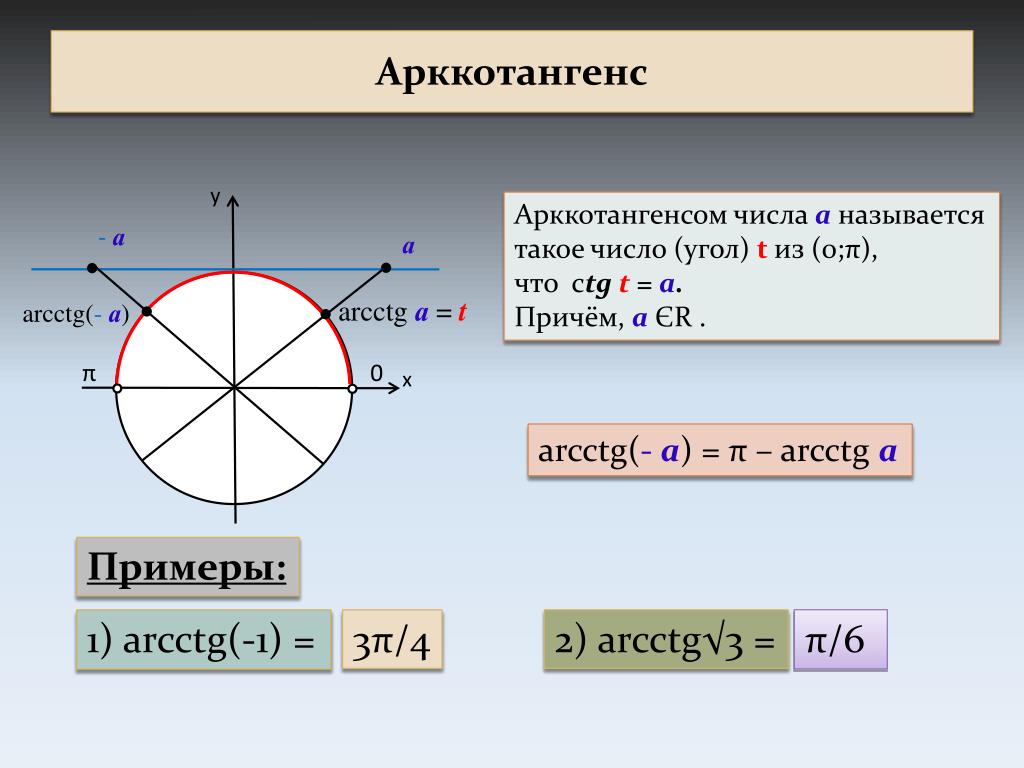 Такая тригонометрическая запись имеет вид arccos12=60°
Такая тригонометрическая запись имеет вид arccos12=60°
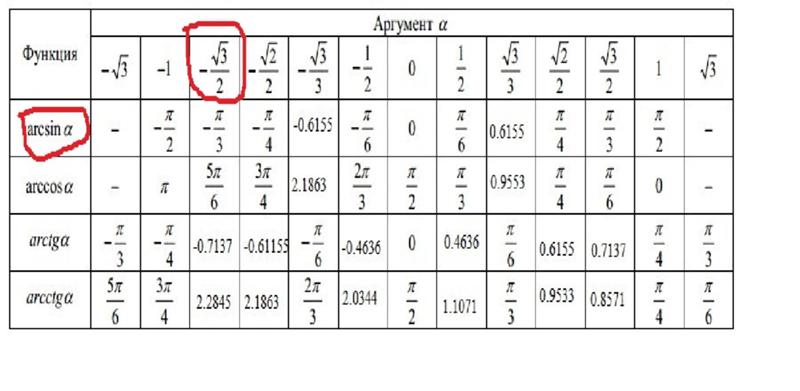
Основные значения arcsin, arccos, arctg и arctg
Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0, ±30, ±45, ±60, ±90, ±120, ±135, ±150, ±180 градусов. Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.
Таблица синусов основных углов предлагает такие результаты значений углов:
sin(-π2)=-1, sin(-π3)=-32, sin(-π4)=-22, sin(-π6)=-12,sin 0 =0, sinπ6=12, sinπ4=22, sinπ3=32, sinπ2=1
Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от -1 и заканчивая 1, также значения от –π2 до +π2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
Ниже приведена таблица арксинуса с радианным и градусным значением углов.
| α | -1 | -32 | -22 | -12 | 0 | 12 | 22 | 32 | |
| arcsin αкак угол | в радианах
| -π2 | -π3 | -π4 | -π6 | 0 | π6 | π4 | π3 |
| в градусах | -90° | -60° | -45° | -30° | 0° | 30° | 45° | 60° | |
| arcsin α как число | -π2 | -π3 | -π4 | -π6 | 0 | π6 | π4 | π3 | |
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
cos 0=1, cos π6=32 , cos π4=22, cos π3=12, cosπ2=0,cos2π3=-12, cos3π4=-22, cos5π6=-32, cosπ=-1
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеСледуя из таблицы, находим значения арккосинуса:
arccos (-1)=π, arccos (-32)=5π6, arcocos (-22)=3π4, arccos-12=2π3, arccos 0 =π2, arccos 12=π3, arccos 22=π4, arccos32=π6, arccos 1 =0
Таблица арккосинусов.
| α | -1 | -32 | -22 | -12 | 0 | 12 | 22 | 32 | 1 | |
| arccos αкак угол | в радианах
| π | 5π6 | 3π4 | 2π3 | π2 | π3 | π4 | π6 | 0 |
| в градусах | 180° | 150° | 135° | 120° | 90° | 60° | 45° | 30° | 0° | |
| arccos α как число | π | 5π6 | 3π4 | 2π3 | π2 | π3 | π4 | π6 | 0 | |
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | -3 | -1 | -33 | 0 | 33 | 1 | 3 | |
| arctg aкак угол | в радианах | -π3 | -π4 | -π6 | 0 | π6 | π4 | π3 |
| в градусах | -60° | -45° | -30° | 0° | 30° | 45° | 60° | |
| arctg a как число | -π3 | -π4 | -π6 | 0 | π6 | π4 | π3 | |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
arcsin, arccos, arctg и arcctg
Для точного значения arcsin, arccos, arctg и arcctg числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения arcsin, arccos, arctg и arcctg отрицательных и положительных чисел сводится к нахождению формул arcsin, arccos, arctg и arcctg противоположных чисел вида arcsin(-α)=-arcsin α, arccos(-α)=π-arccos α, arctg(-α)=-arctg α, arcctg(-α)=π-arcctg α.
Рассмотрим решение нахождения значений arcsin, arccos, arctg и arcctg с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0,2857, ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0,2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0,2863 используется та самая поправка в 0,0006, так как ближайшим числом будет 0,2857. Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения arcsin, arccos, arctg и arcctg.
Нахождение значения arcsin, arccos, arctg и arcctg
Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы arcsin α+arccos α=π2, arctg α+arcctg α=π2 (не обходимо просмотреть тему формул суммы арккосинуса и арксинуса, суммы арктангенса и арккотангенса).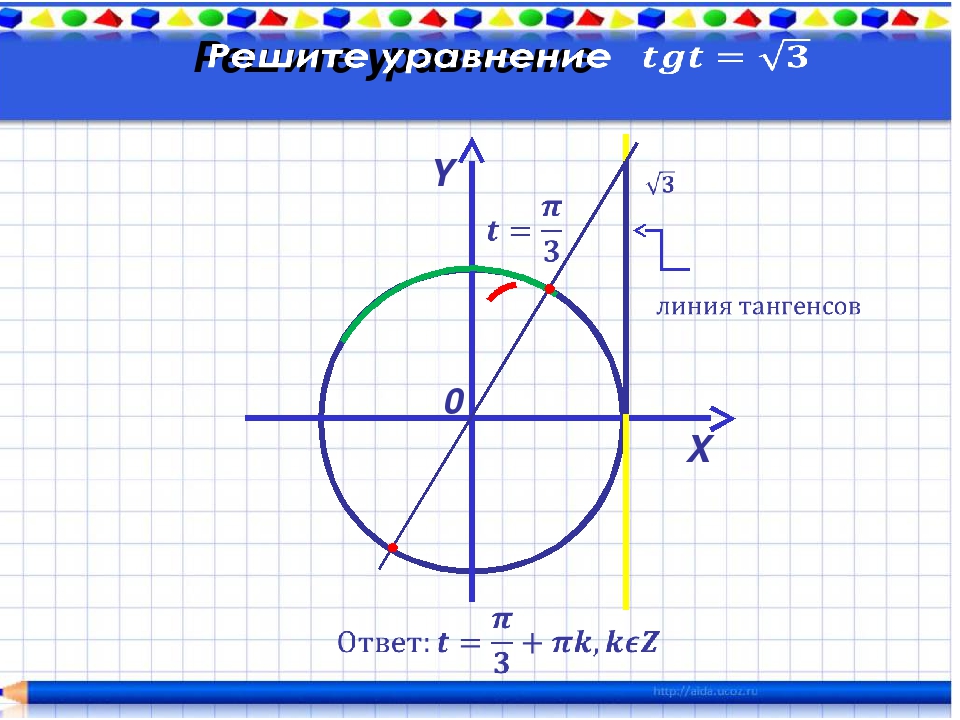
При известном arcsin α= -π12 необходимо найти значение arccos α, тогда необходимо вычислить арккосинус по формуле:
arccos α=π2−arcsin α=π2−(−π12)=7π12.
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Если дан арккосинус числа а равный π10, а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0,9511, после чего заглядываем в таблицу Брадиса.
При поиске значения арктангенса 0,9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Математика для блондинок: Арктангенс на калькуляторе
Как всегда, самое интересное происходит в комментариях.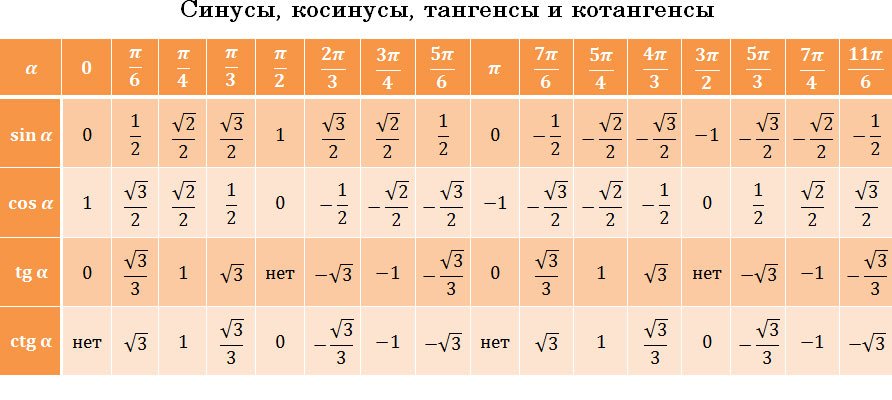 Вот один из последних:
Вот один из последних:Извините за беспокойство.
Для супруги тут понадобилась
тригонометрия, для юридического(!) института (маленький курс информатики
— раздел «работа с калькулятором»). С синусами и косинусами я
(завязавший с алгеброй 10 лет назад) кое-как разобрался.
В ступор вводит «элементарный» вопрос…
Есть tg3х=4, надо вычислить угол «х»…
Не знаю с какой стороны подойти…
Разъясните… Спасибо.
Этого зверя приручают через обратные тригонометрические функции. В нашем случае нужно использовать арктангенс. Выглядит это приблизительно вот так:
tg3х=4
arctg(tg3х)=arctg4
Дальше довольно просто (объясняю для юридического))))))) — арктангенс тангенса равен просто углу, в данном случае 3х. Это типа украсть и положить обратно))) Дословный перевод с бытовухи на язык тригонометрии будет звучать приблизительно так:
«Украли угол 3х» — tg3x;
«Украли и положили на место угол
3х» — arctg(tg3x).
Теперь совсем детский вопрос: «Что у на лежит на
месте?».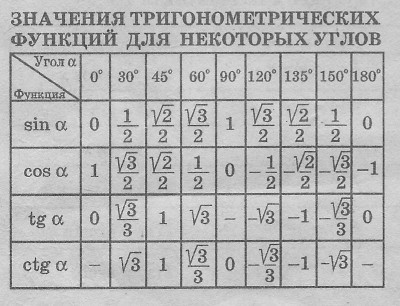 Правильно, угол 3х. С левой частью мы разобрались.
Правильно, угол 3х. С левой частью мы разобрались.
Рассмотрим правую часть. Тупые менты обнаружили у скупщика краденного число 4. Из оперативных данных известно, что перекупщик сдал краденный угол по курсу тангенса. Вопрос не для тупых ментов: «Какой угол был украден, если скупщик краденного по курсу тангенса получил за него число 4?». Для ответа на этот вопрос мы можем использовать таблицу значений тангенса в качестве прейскуранта обмена углов на числа среди скупщиков краденного. Но у нас тупо задана тема «работа с калькулятором». Значит мы обязаны пользоваться не бумажной таблицей (в век планшетов смешно звучит), а пластмассовым калькулятором.
Как найти арктангенс на калькуляторе? Я воспользуюсь тем, что у меня всегда под рукой. В калькуляторе «Виндовс» вводим число 4, затем нажимаем кнопочку «Inv».
| Арктангенс на калькуляторе. Шаг 1. |
 На этой кнопочке должна появиться степень минус
единичка. Четверка должна оставаться неизменной.
На этой кнопочке должна появиться степень минус
единичка. Четверка должна оставаться неизменной. | Арктангенс на калькуляторе. Шаг 2. |
Вот теперь нажимаем кнопочку тангенса в минус первой степени и получаем значение угла, тангенс которого равен 4. Если у нас на калькуляторе включен пыптик «Градусы», то получим 75,963756532073521417107679840837 градусов.
| Арктангенс на калькуляторе. Шаг 3. |
| Арктангенс в радианах |
tg3х=4
arctg(tg3х)=arctg4
3х=75,964
х=75,964/3
х=25,321 (градуса)
То же самое, но теперь в радианах:
tg3х=4
arctg(tg3х)=arctg4
3х=1,326
х=1,326/3
х=0,442 (радиан)
Если у вас в руках калькулятор какой-либо другой конструкции, то вам нужно методом научного тыка выковырять из калькулятора нужный результат)))
Справедливости ради нужно отметить, что инквизиторы от математики могут потребовать учесть в ответе периодичность тригонометрической функции тангенс. В этом случае к полученному ответу добавляем маразм в виде «плюс пи эн» (для радиан) или «плюс 180 эн». Специально для особо ортодоксальных математиков можно указать, что эн равно нулю, плюс-минус единице, плюс-минус два и так далее до скончания века, пардон, чисел.
В этом случае к полученному ответу добавляем маразм в виде «плюс пи эн» (для радиан) или «плюс 180 эн». Специально для особо ортодоксальных математиков можно указать, что эн равно нулю, плюс-минус единице, плюс-минус два и так далее до скончания века, пардон, чисел.
Ну, и особенно меня порадовал ответ на мои объяснения.
…Огромная вам благодарность за это
математическое расследование…
Ваше объяснение настолько вдохновило, что на этой волне мы с супругой решили все «задачи с калькулятором». Ещё раз спасибо!
P.S.
Почитал ваш профиль в гугле. И скажу, что ещё как гражданин России,
разделяю ваши взгляды на террористические Донецк и Луганск. Желаю сил
вам и украинскому народу додавить террористов и потихоньку возвращать
себе К.R.Ы.М. Мы верим в Украину без кRемлR! Успехов вам!
Я тоже верю, что донецких и луганских террористов мы замочим даже в кремлевском сортире, что российская армия уберется с Украины, что путин перестанет совать свое свиное рыло в чужие дела и что Крым снова будет Украиной.
Arccos arcsin arctg arcctg — Вэб-шпаргалка для интернет предпринимателей!
Содержание
- 1 Арксинус, arcsin
- 2 Арккосинус, arccos
- 3 Четность
- 4 Свойства — экстремумы, возрастание, убывание
- 5 Таблица арксинусов и арккосинусов
- 6 Формулы
- 7 Синус арксинуса, косинус арккосинуса и т.п.
- 8 Арксинус синуса, арккосинус косинуса и т.п.
- 9 Связи между arcsin, arccos, arctg и arcctg противоположных чисел
- 10 Сумма арксинуса и арккосинуса числа, сумма арктангенса и арккотангенса числа
- 11 Синус от арккосинуса, тангенс от арксинуса и иже с ними
- 12 arcsin через arccos, arctg и arcctg; arccos через arcsin, arctg и arcctg и т.п.
- 13 Некоторые другие формулы
Арксинус, arcsin
Определение и обозначения
Арксинус иногда обозначают так:
.
График функции арксинус
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Определение и обозначения
Арккосинус иногда обозначают так:
.
График функции арккосинус
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(– x ) = arcsin(–sin arcsin x ) = arcsin(sin(–arcsin x )) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(– x ) = arccos(–cos arccos x ) = arccos(cos(π–arccos x )) = π – arccos x ≠ ± arccos x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см.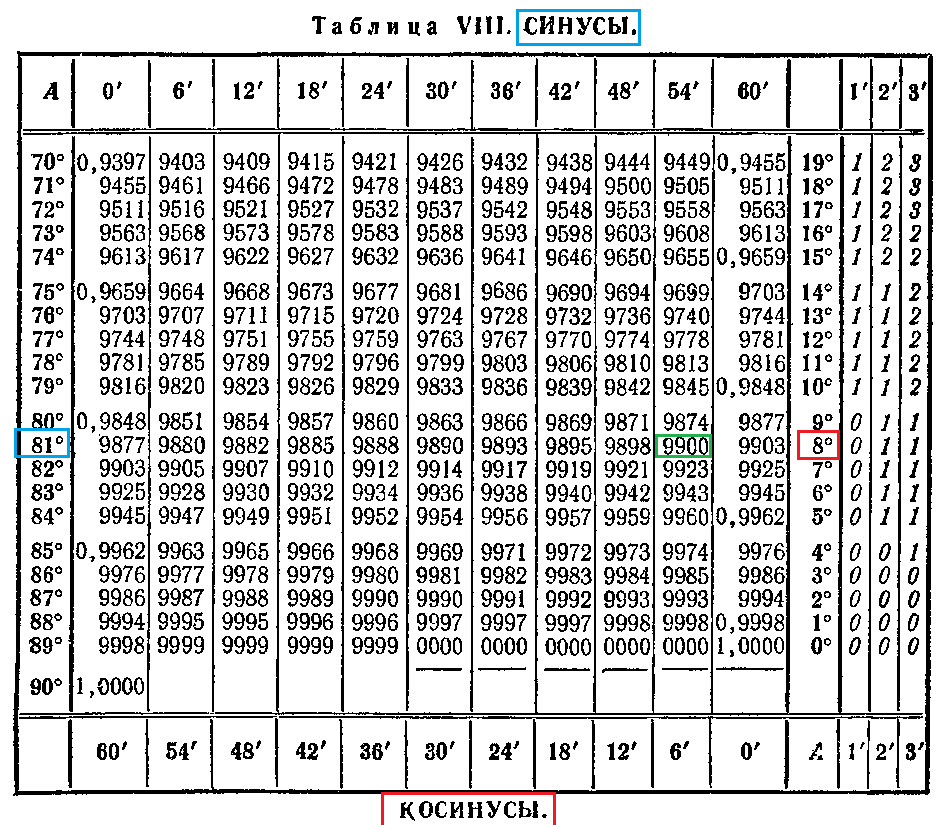 доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/ 2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| – 1 | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0° | 90° | |||
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° |
Формулы
Формулы суммы и разности
при или
при 0,,y>0 ;»> и 1″>
при и 1″>
при или
при 0,,y и 1″>
при 0 ;»> и 1″>
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов. Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.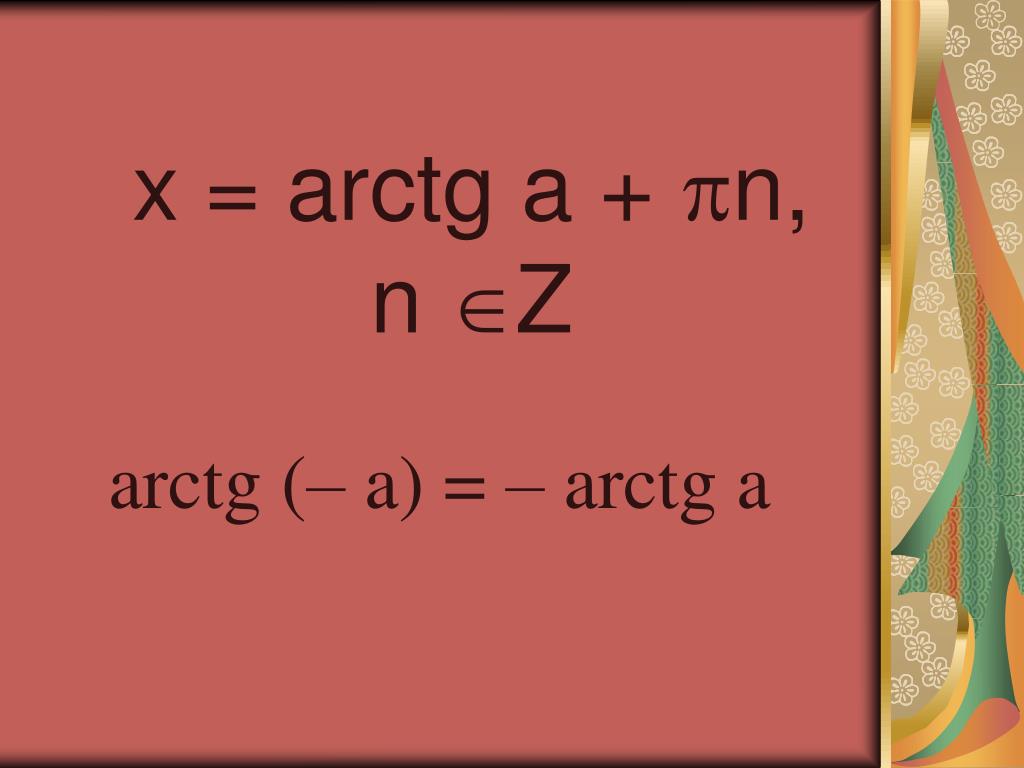 ) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс.
) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс.
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8. Скока-скока!? 1,8!? Косинус не бывает больше единицы.
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов. Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус.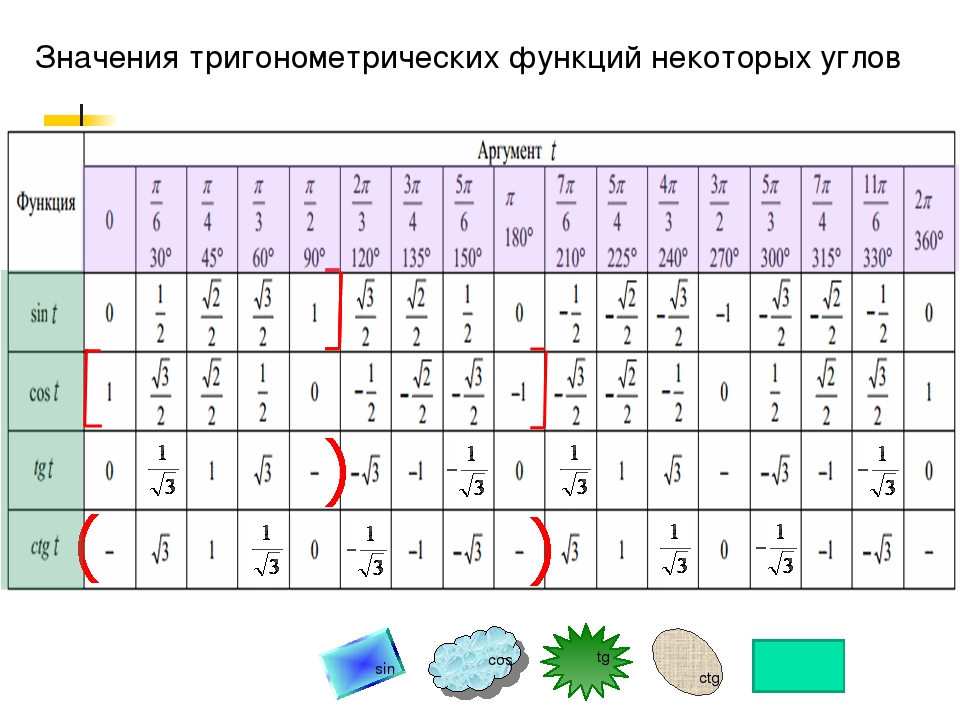 Что такое арктангенс, арккотангенс. То легко разберётесь, например, с таким монстром.)
Что такое арктангенс, арккотангенс. То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да. ) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого. Ну и так далее. Если сведущий человек знает ещё и таблицу синусов. Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё. Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8). Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Типа, arctg(-1,3), или, к примеру, arccos(-0,8). Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
Те, кто освоил темы «Тригонометрический круг», и «Отсчёт углов на тригонометрическом круге» — люди грамотные. И, возможно, уже приготовили мне убойный вопрос.) По определению, скажем, arcsin 0,5 — это угол, синус которого равен 0,5. Т.е 30°. Но.
Грамотный человек знает, что синус равен 0,5 не только у угла 30°! Так как:
И так до бесконечности.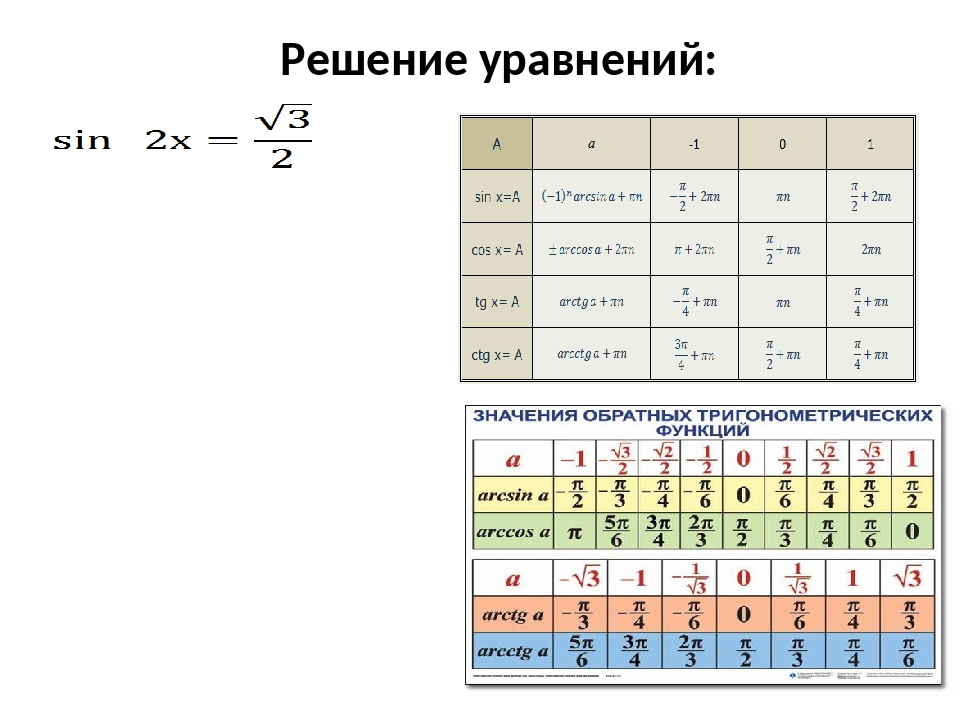 Неоднозначно получается! Получается, что arcsin0,5 это и 30°, и 150°, и 390°, и 510°, и .
Неоднозначно получается! Получается, что arcsin0,5 это и 30°, и 150°, и 390°, и 510°, и .
Да. Именно так. Арксинус 0,5 — это действительно бесконечный набор углов. Но обозначается такой арксинус вот как: Arcsin0,5. С заглавной буквы. В школе такие арксинусы не изучают. В школе изучают арки с маленькой буквы: arcsin, arccos, arctg, arcctg. Такие арки называются главными значениями арксинуса, арккосинуса и т.д. и имеют жёсткие ограничения по величине. Для однозначности.
С этими ограничениями надо разобраться основательно. Тем более, что это дело простое.) Запоминаем:
arсsin (любой) — это угол, который располагается в интервале:
arсcos (любой) — это угол, который располагается в интервале:
arсtg (любой) — это угол, который располагается в интервале:
arсctg (любой) — это угол, который располагается в интервале:
Запомнить эти диапазоны очень легко по картинкам. Тригонометрический круг вам в помощь!) Для арксинуса:
Тригонометрический круг вам в помощь!) Для арксинуса:
Зелёным нарисованы углы, которые пробегают значения от — Пи/2 до + Пи/2. Это и есть разрешённая зона для арксинусов. И никаких дополнительных оборотов! Строго от -90° до +90°! Никакой arcsin не может быть равным, например 120°, 180° или 330°. А вот 50°, -65°, 90° или 25° — пожалуйста!
Теперь, я думаю, понятно, что arcsin 0,5 = 30°. И только 30°! Так как углы 150°, 390°, 510° и т.д., которые тоже дают синус, равный 0,5, арксинусами быть не могут. Они выпадают из разрешённого диапазона.
А теперь наведите курсор мышки на рисунок, или коснитесь картинки на планшете. Вы увидите диапазон арктангенсов. Найдите 2 отличия.) Да! Конечные точки на оси ОУ стали белыми! Это означает, что они не включаются в диапазон арктангенсов. Арктангенс не может быть равным ±90°. По той простой причине, что тангенс 90° (и -90°) не существует.
Уже проще, правда?) Ну и, аналогичная картинка для арккосинуса и арккотангенса (при наведённом курсоре):
Надеюсь, зрительная память вас спасёт, если что. )
)
А зачем все эти арки? — слышу ещё один осторожный вопрос.)
Вопрос резонный. В математике просто так, чисто для красоты, ничего не бывает. Только по острой необходимости!) А вы попробуйте ответить на такой вопрос:
У какого угла синус равен 0,4?
Для ответа в градусах или радианах вам придётся открывать таблицы Брадиса, или включать солидный калькулятор. Искать там значение синуса, равное (примерно!) 0,4 и смотреть, какой же угол имеет этот синус. После тяжких трудов вы определите, что это угол примерно 23 градуса и 36 минут. Про радианы я вообще молчу. )
А через арксинус мгновенно даётся абсолютно точный ответ: угол, у которого синус равен 0,4 — это arcsin 0,4 ! Просто по смыслу арксинуса: arcsin 0,4 — это и есть угол, синус которого равен 0,4. Разумеется, это не единственный угол, синус которого равен 0,4, но через арки и все остальные записываются в три секунды. Этим мы в тригонометрических уравнениях займёмся.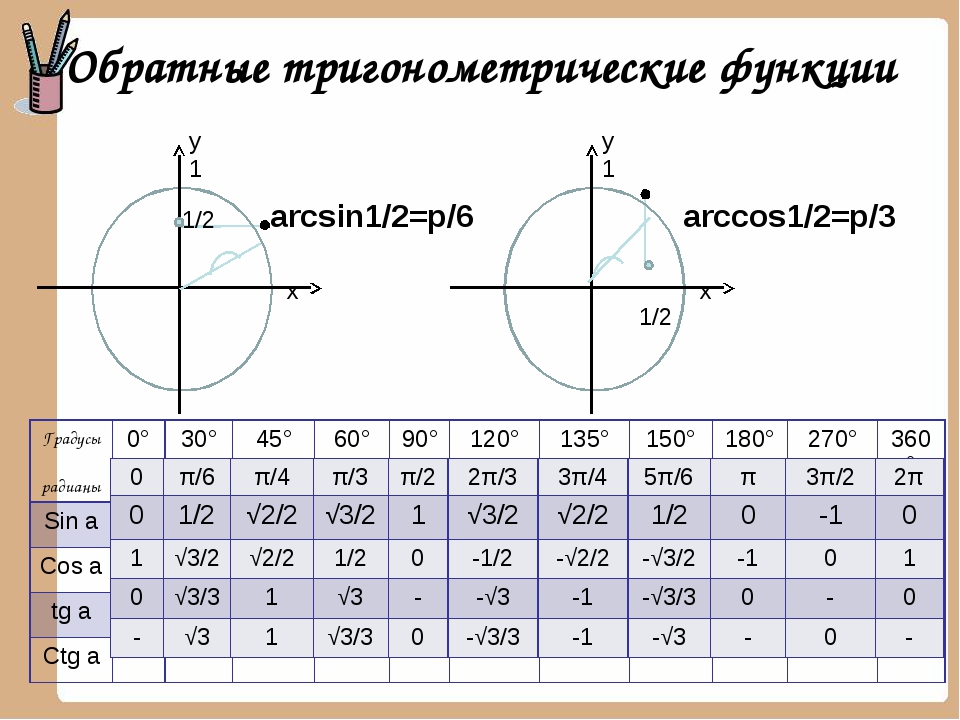
Если вы осознали этот забавный факт, то легко ответите на все подобные вопросы:
У какого угла синус равен -0,7 ?
У угла arcsin (-0,7).
У какого угла косинус равен 0,03 ?
У угла arccos 0,03.
У какого угла тангенс равен 3 ?
У угла arctg 3.
У какого угла котангенс равен 0,123 ?
У угла arcctg 0,123.
Вам кажутся странными эти вопросы? Привыкайте.) Это главные вопросы любого тригонометрического уравнения. Для решения таких уравнений арки подходят — лучше некуда.
Здесь важно понимать, что arcsin (-0,7), arctg 3 и т.п. — это просто какие-то числа, величины углов. И отличаются от привычных градусов или радианов только компактной формой записи. Например, можно записать (точно!) величину угла в виде:
А можно записать (приблизительно) тот же самый угол через градусы. Это будет:
≈ 23,57817847820183110402.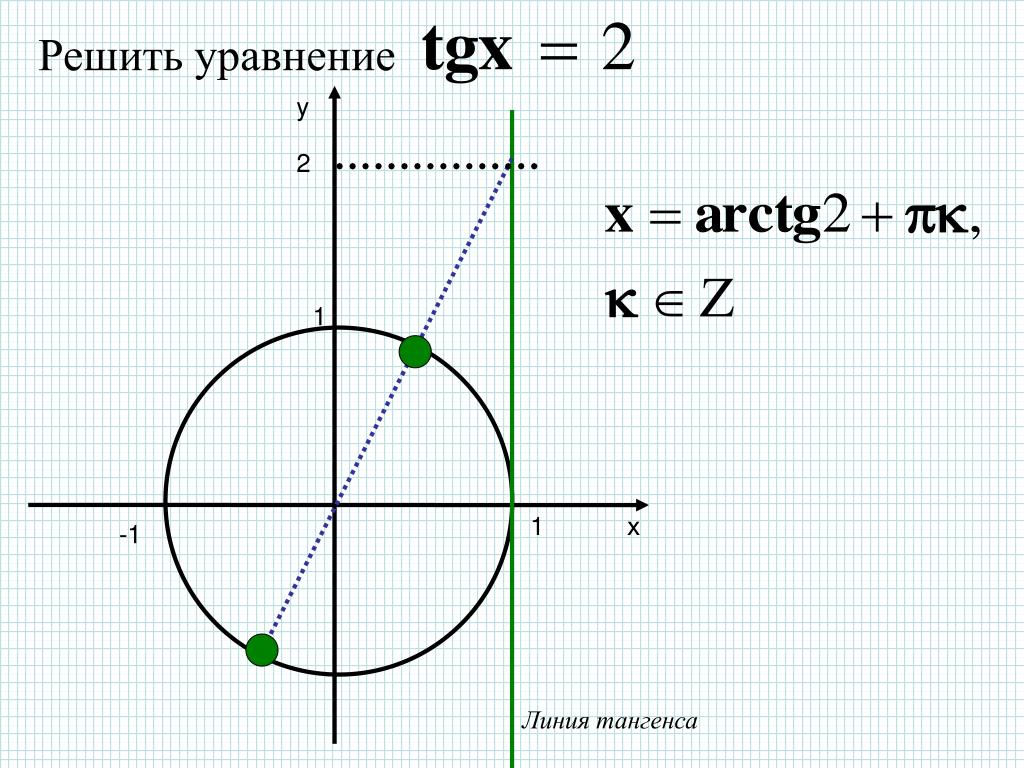 °
°
Осознали простой и важный смысл арков? Тогда порешаем самостоятельно. Примерчики от устных до хитрых.)
Для успешной работы с арксинусами, арккосинусами, арктангенсами и арккотангенсами чисел нужно знать существующие между ними связи. Эти связи удобно записывать в виде формул.
В этой статье мы разберем основные формулы с arcsin, arccos, arctg и arcctg, для удобства работы и запоминания разобьем эти формулы по группам, дадим их вывод и доказательство, а также покажем примеры использования.
Навигация по странице.
Первые четыре блока формул представляют собой основные свойства арксинуса, арккосинуса, арктангенса и арккотангенса числа, в указанной статье сайта www.cleverstudents.ru Вы найдете и доказательство этих формул, и примеры их применения. Здесь мы не будем повторяться, а лишь приведем сами формулы, чтобы они все были в одном месте.
Синус арксинуса, косинус арккосинуса и т.п.
Эти формулы очевидны и напрямую следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса числа. Они показывают, чему равен синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса.
Они показывают, чему равен синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса.
Арксинус синуса, арккосинус косинуса и т.п.
Эти формулы также очевидны и следуют из определений арксинуса, арккосинуса, арктангенса и арккотангенса. Они определяют, чему равен арксинус синуса, арктангенс тангенса, арккосинус косинуса и арккотангенс котангенса. Заметим, что стоит быть очень внимательными к указанным условиям, так как если угол (число) α выходит за указанные пределы, то эти формулы использовать нельзя, ибо они дадут неверный результат.
Связи между arcsin, arccos, arctg и arcctg противоположных чисел
Формулы этого блока показывают, как арксинус, арккосинус, арктангенс и арккотангенс отрицательного числа выражаются через arcsin , arccos , arctg и arcctg противоположного ему положительного числа. Эти формулы позволяют избавиться от работы с арксинусами, арккосинусами, арктангенсами и арккотангенсами отрицательных чисел, и перейти к работе с этими аркфункциями от положительных чисел.
Сумма арксинуса и арккосинуса числа, сумма арктангенса и арккотангенса числа
Записанные формулы позволяют выразить арксинус числа через арккосинус этого же числа, арккосинус через арксинус, арктангенс через арккотангенс и арккотангенс через тангенс того же числа.
Синус от арккосинуса, тангенс от арксинуса и иже с ними
На практике очень полезными оказываются формулы, устанавливающие отношения между тригонометрическими функциями и аркфункциями. К примеру, может потребоваться вычислить синус арккосинуса некоторого числа, или тангенс арксинуса. Запишем список формул, позволяющих решать подобные задачи, дальше покажем примеры их применения и приведем доказательства этих формул.
Приведем несколько примеров использования записанных формул. Например, вычислим косинус арктангенса корня из пяти. Соответствующая формула имеет вид , таким образом .
Другой пример: используя формулу синуса арккосинуса вида , мы можем вычислить, к примеру, синус арккосинуса одной второй, имеем . Заметим, что в этом примере вычисления можно провести и непосредственно, они приводят к тому же результату: (при необходимости смотрите статьи вычисление значений синуса, косинуса, тангенса и котангенса и вычисление значений арксинуса, арккосинуса, арктангенса и арккотангенса).
Заметим, что в этом примере вычисления можно провести и непосредственно, они приводят к тому же результату: (при необходимости смотрите статьи вычисление значений синуса, косинуса, тангенса и котангенса и вычисление значений арксинуса, арккосинуса, арктангенса и арккотангенса).
Осталось показать вывод записанных формул.
Формулы, находящиеся в ячейках таблицы на диагонали, есть формулы синуса арксинуса, косинуса арккосинуса и т.д. Они были получены ранее, поэтому не нуждаются в доказательстве, и их мы будем использовать для доказательства остальных формул. Более того, для вывода формул нам еще потребуются основные тригонометрические тождества.
Выведем сначала формулу синуса арккосинуса, синуса арктангенса и синуса арккотангенса. Из основных тригонометрических тождеств и , а также учитывая, что , легко получить следующие формулы , и , выражающие синус через косинус, синус через тангенс и синус через котангенс при указанных условиях. Подставляя arccos a вместо альфа в первую формулу, получаем формулу синуса арккосинуса; подставляя arctg a вместо альфа во вторую формулу, получаем формулу синуса арктангенса; подставляя arcctg a вместо альфа в третью формулу, получаем формулу синуса арктангенса.
Вот краткая запись вышеперечисленных выкладок:
По аналогии легко вывести формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса:
Теперь покажем вывод формул тангенса арксинуса, тангенса арккосинуса и тангенса арккотангенса:
Формулы котангенса арксинуса, котангенса арккосинуса и котангенса арктангенса легко получить из формул тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса, поменяв в них числитель и знаменатель, так как .
arcsin через arccos, arctg и arcctg; arccos через arcsin, arctg и arcctg и т.п.
Из формул связи тригонометрических и обратных тригонометрических функций, разобранных в предыдущем пункте, можно получить формулы, выражающие одну из аркфункций через другие аркфункции, например, выражающие арксинус одного числа, через арккосинус, арктангенс и арккотангенс другого числа. Перечислим их.
По этим формулам можно заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно:
Вот формулы, выражающие арккосинус через арксинус, арктангенс и арккотангенс:
Формулы арктангенса через арксинус, арккосинус и арккотангенс имеют следующий вид:
Наконец, вот ряд формул с арккотангенсом:
Доказать все записанные формулы можно, отталкиваясь от определений арксинуса, арккосинуса, арктангенса и арккотангенса числа, а также формул из предыдущего пункта.
Для примера, докажем, что . Известно, что при указанных a представляет собой угол (число) от минус пи пополам до пи пополам. Более того, по формуле синуса арктангенса имеем . Следовательно, при −1 является арксинусом числа a по определению, то есть, .
По аналогии можно доказать и остальные формулы, представленные в данном пункте статьи.
В заключение этого пункта покажем пример использования полученных формул. Для примера вычислим с их помощью, чему равен синус арккотангенса минус корня из трех. Обратившись к формуле вида , выражающей арккотангенс через арксинус, при имеем .
В данном примере мы могли вычислить требуемое значение и непосредственно: . Очевидно, что мы получили тот же результат.
Понятно, что для вычисления требуемого значения мы могли поступить и иначе, воспользовавшись формулой, выражающей синус через котангенс вида . Тогда решение выглядело бы так: . А можно было и сразу применить формулу синуса арккотангенса вида : .
Некоторые другие формулы
Основные формулы тригонометрии и формулы синуса арксинуса, косинуса арккосинуса, тангенса арктангенса и котангенса арккотангенса позволяют вывести ряд формул с arcsin , arccos , arctg и arcctg , еще не упомянутых в данной статье. Но заметим, что они уже достаточно специфичны, и приходится их использовать далеко не часто. Более того, такие формулы удобнее каждый раз выводить, нежели запоминать.
Но заметим, что они уже достаточно специфичны, и приходится их использовать далеко не часто. Более того, такие формулы удобнее каждый раз выводить, нежели запоминать.
Для примера возьмем формулу половинного угла . Если добавить условие, что величина угла альфа принадлежит отрезку от нуля до пи, то будет справедливо равенство . При указанном условии угол альфа можно заменить на арккосинус числа a , что нам даст формулу вида , откуда можно получить следующую формулу, выражающую арккосинус через арксинус: .
Используя другие тригонометрические формулы, можно обнаружить ряд других связей между arcsin , arccos , arctg и arcctg .
В заключение этого пункта хочется сказать, что практическую пользу представляют даже не столько сами эти специфические формулы, связывающие arcsin , arccos , arctg и arcctg , сколько умения выполнять преобразования, используемых при выводе этих формул. Продолжением темы служит раздел теории преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом. (- x) относительно x
(- x) относительно x
Arctan бесплатный онлайн-калькулятор | Justfreetools
Онлайн калькулятор arctan (x).Калькулятор арктангенса.
Калькулятор тангенса »
Определение арктангенса
Функция арктангенса является обратной функцией y = tan (x).
arctan ( y ) = tan -1 ( y ) = x + kπ
За каждые
k = {…, — 2, -1,0,1,2, …}
Например, если тангенс 45 ° равен 1:
загар (45 °) = 1
Тогда арктангенс 1 равен 45 °:
арктан (1) = загар -1 (1) = 45 °
Таблица арктангенса
| y | x = arctan (y) | |
|---|---|---|
| градуса | радиан | |
-1.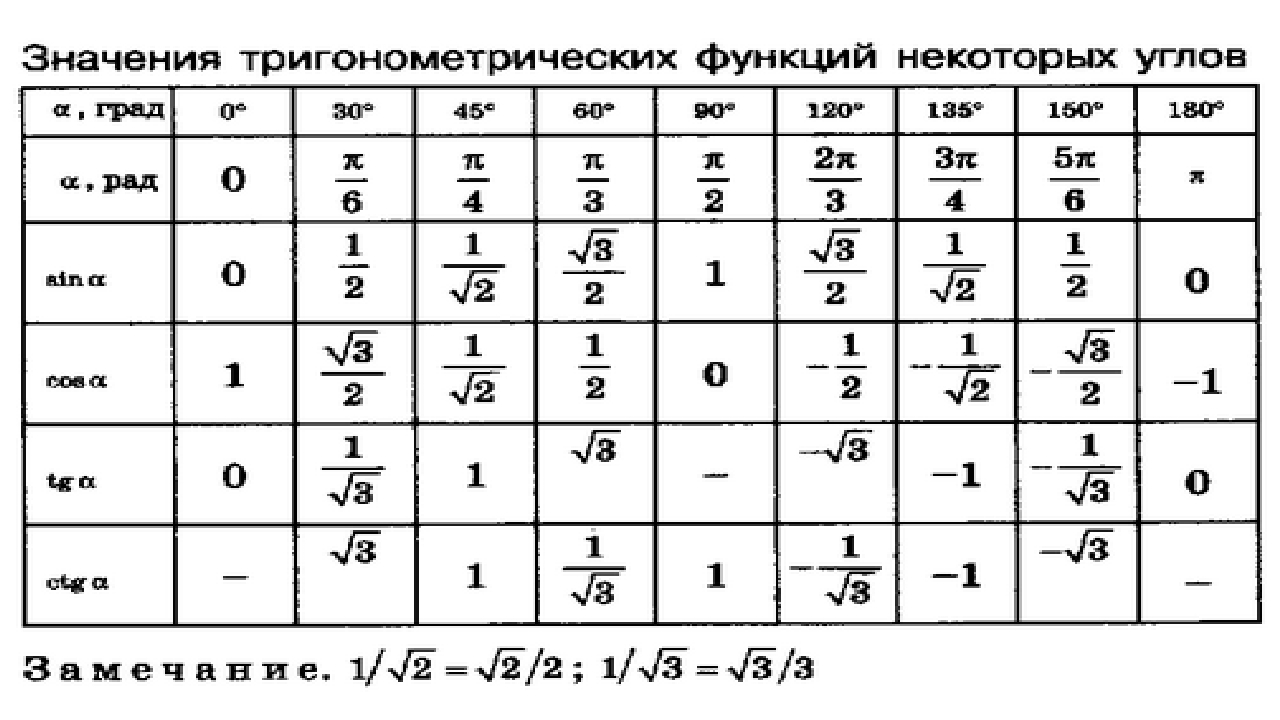 732050808 732050808 | -60 ° | -π / 3 |
| -1 | -45 ° | -π / 4 |
| -0,577350269 | -30 ° | -π / 6 |
| 0 | 0 ° | 0 |
| 0,577350269 | 30 ° | π / 6 |
| 1 | 45 ° | π / 4 |
| 1.732050808 | 60 ° | π / 3 |
Arctan на калькуляторе
Чтобы вычислить arctan (y) на калькуляторе:
- Нажать Shift + желтые кнопки.
- Введите угол.
- Нажмите кнопку Рассчитать .
Калькулятор тангенса »
В настоящее время у нас есть около 929 калькуляторов и таблиц преобразования, которые помогут вам быстро «вычислить» в таких областях, как:
И мы все еще разрабатываем другие. Наша цель — стать универсальным сайтом для людей, которым нужно быстро производить расчеты или которым нужно быстро найти ответ на основные конверсии.
Наша цель — стать универсальным сайтом для людей, которым нужно быстро производить расчеты или которым нужно быстро найти ответ на основные конверсии.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Таким образом, все наши инструменты и услуги полностью бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметили малейшую ошибку — ваш вклад очень важен для нас.Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
Нашли ошибку? Дайте нам знать !
Мы получили ваше сообщение, мы свяжемся с вами в ближайшее время.
Ой! Что-то пошло не так, обновите страницу и попробуйте еще раз.
Тригонометрическая функция arctan () — арктангенс — определение математического слова
Тригонометрическая функция arctan () — арктангенс — определение математического слова — Math Open Reference Функция арктангенса — это функция, обратная касательной.
Возвращает угол, тангенс которого является заданным числом.
Для каждой тригонометрической функции существует обратная функция, которая работает наоборот. Эти обратные функции имеют то же имя, но с дугой впереди. (На некоторых калькуляторах кнопка arctan может быть помечена как атан, а иногда загар -1 .) Таким образом, тангенс, обратный tan, равен arctan и т. Д. Когда мы видим «arctan x», мы понимаем его как «угол, тангенс которого равен x».
| загар 30 = 0,577 | Означает: тангенс 30 градусов равен 0,577 |
арктан 0. 577 = 30 577 = 30 | Означает: угол, тангенс которого равен 0,577, равен 30 градусам. |
См. Также Обратные функции — тригонометрия
Пример — использование arctan для нахождения угла
На приведенном выше рисунке нажмите «Сброс».
Нам известны длины сторон, но нам нужно найти величину угла C.
Мы знаем, что поэтому нам нужно знать угол, тангенс которого равен 0,577, или формально: С помощью калькулятора находим arctan 0.577 — 30 °.
Большие и отрицательные углы
Напомним, что мы можем применить
Триггерные функции на любой угол, включая большие и отрицательные углы. Но когда мы
Рассмотрим обратную функцию, и мы столкнемся с проблемой, потому что существует бесконечное количество углов, имеющих одинаковую касательную.
Например, 45 ° и 360 + 45 ° будут иметь одинаковую касательную. Подробнее об этом см.
Обратные тригонометрические функции.
Чтобы решить эту проблему, классифицировать обратных триггерных функций ограничены таким образом, чтобы обратные функции были взаимно однозначными, то есть для каждого входного значения был только один результат.
Диапазон и домен arctan
Напомним, что область определения функции — это набор допустимых входных данных для нее. Диапазон — это набор возможных выходов.
Для y = arctan x:
| Диапазон | |
| Домен | Все числа |
По соглашению диапазон arctan ограничен от -90 ° до + 90 ° * .
Итак, если вы используете калькулятор для решения, скажем, arctan 0.55, из бесконечного числа возможностей он вернет 28,81 °, тот, который находится в диапазоне функции.
* На самом деле, -90 ° и + 90 ° сами по себе не входят в диапазон. Это потому, что функция tan имеет значение
бесконечность при этих значениях.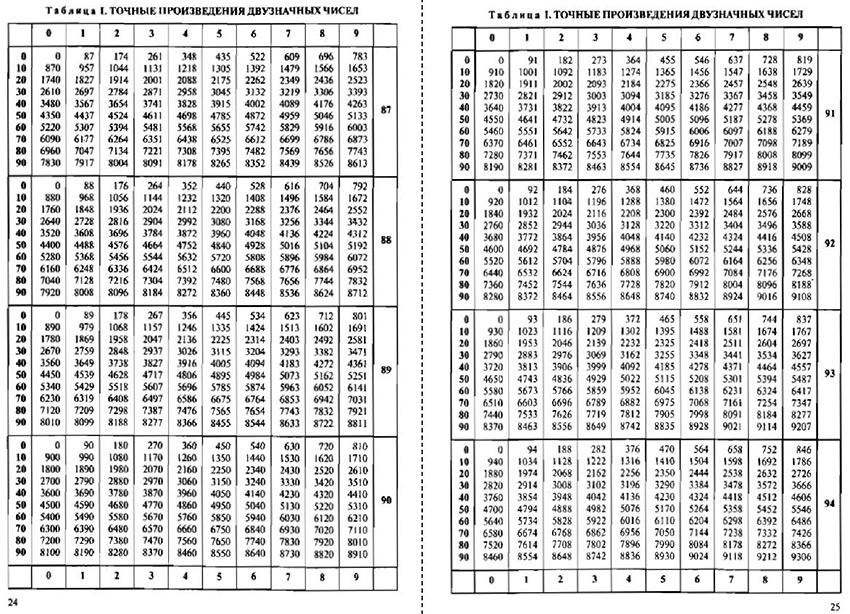 Но значения чуть ниже них находятся в диапазоне, например +89.9999999. Но для простоты объяснения
мы говорим, что диапазон составляет ± 90 °.
Но значения чуть ниже них находятся в диапазоне, например +89.9999999. Но для простоты объяснения
мы говорим, что диапазон составляет ± 90 °.
Что попробовать
- На рисунке выше нажмите «сбросить» и «скрыть детали».
- Отрегулируйте треугольник до нового размера
- Используя функцию arctan, вычислите значение угла C из длин сторон
- Щелкните «Показать подробности», чтобы проверить ответ.
Другие темы по тригонометрии
Уголки
Тригонометрические функции
Решение задач тригонометрии
Исчисление
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
арктан 1 + арктан 2 + арктан 3 =?
Доказательство: По стандартному тангенсу суммы,
tan tan
tan () 1 tan tan
AB
ABAB
+
+ = —
, поэтому
tan tan (tan () ) (1 загар загар) загар () загар загар загар () ABABABABABA B + = + — = + — +
.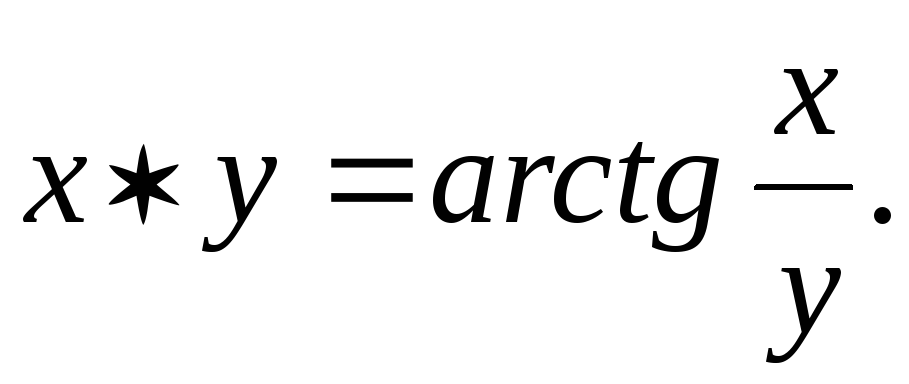
But
tan tan (()) tan () CABAB
π
= — + = — +
, поэтому tan A + tan B + tan C = tan A tan B tan C.
Комментарий: Опять же, частичное обращение можно сделать еще лучше. Я утверждаю, что для 0 <
A, B, C < / 2 мы имеем
tan tan tan tan tan tanA B C A B C + + =
тогда и только тогда, когда
. Я оставляю это на ваше усмотрение, чтобы предоставить детали части обратного значения.
Следствие: ArcTan 1 + ArcTan 2 + ArcTan 3 = от A = ArcTan 1, B = ArcTan 2 и
C = ArcTan 3.В частности, 1 + 2 + 3 = 1 * 2 * 3 = 6.
(Кроме того: 6 является особенным в других отношениях. Это единственное натуральное число, которое одновременно является совершенным и идеально подходит для произведения
, т.е. сумма и произведение его аликвотных делителей.)
Следствие: С точностью до подобия существует только один треугольник ABC, углы которого имеют целые
касательных (tan A = 1, tan B = 2, tan C = 3).
С учетом триггерного тождества (*) это сводится к решению x + y + z = xyz, где x = tan A,
y = tan B и z = tan C.Таким образом, мы приходим к решению этого диофантова уравнения; т.е. мы
ищем решения (x, y, z) в натуральных числах. Вы можете попробовать это сами, чтобы убедиться, что, помимо перестановок
, (1, 2, 3) является единственным решением. Или см. [3] для полного обсуждения.
Сложная головоломка: на квадратном листе бумаги сложите его столько раз, сколько возможно
, чтобы получить углы, размеры которых равны ArcTan 1, ArcTan 2 и ArcTan 3. (Складывание
учитывается, даже если его единственная цель — найти точку.)
Связанный вопрос: игнорируя предыдущие доказательства, можем ли мы использовать только геометрию конструкции
, чтобы доказать идентичность названия,
1 1 1
(1) (2) (3) Tan Tan Tan
π
— — —
+ + =
?
Мы можем обрабатывать оба вопроса одновременно. Мы произведем конструкцию, в которой
Мы произведем конструкцию, в которой
Mathwords: Inverse Tangent
Обратный тангенс
tan -1
Tan -1
arctan
Arctan
Функция, обратная касательной.
Основная идея : найти загар -1 1, мы спрашиваем «какой угол имеет тангенс, равный 1?» Ответ составляет 45 °. В результате мы говорим, что tan -1 1 = 45 °. В радианах это загар -1 1 = π / 4.
Подробнее : На самом деле существует много углов,
касательная равна 1. Мы действительно спрашиваем, «что является самым простым,
самый основной угол, тангенс которого равен 1? «Как и прежде,
ответ — 45 °.Таким образом, загар -1 1
= 45 ° или tan -1 1 = π / 4.
Подробности : Что такое загар -1 (–1)? Выбираем ли мы 135 °, –45 °, 315 °, или под другим углом? Ответ –45 °. Обратной тангенсой выбираем угол на правой половине единицы круг, имеющий размер как можно ближе к нулю. Таким образом, загар -1 (–1) = –45 ° или тангенциальный угол -1 (–1) = –π / 4.
В другими словами, диапазон tan -1 равен ограничено (–90 °, 90 °) или.
Примечание : arctan означает «арктангенс» или радианную меру дуга на окружности, соответствующая заданному значению касательной.
Техническое примечание : Поскольку ни одна из шести триггерных функций синус, косинус, тангенс, косеканс, секанс и котангенс не взаимно однозначны,
их инверсии не являются функциями. Каждая триггерная функция может иметь свой
Однако домен ограничен, чтобы сделать его обратным функцией.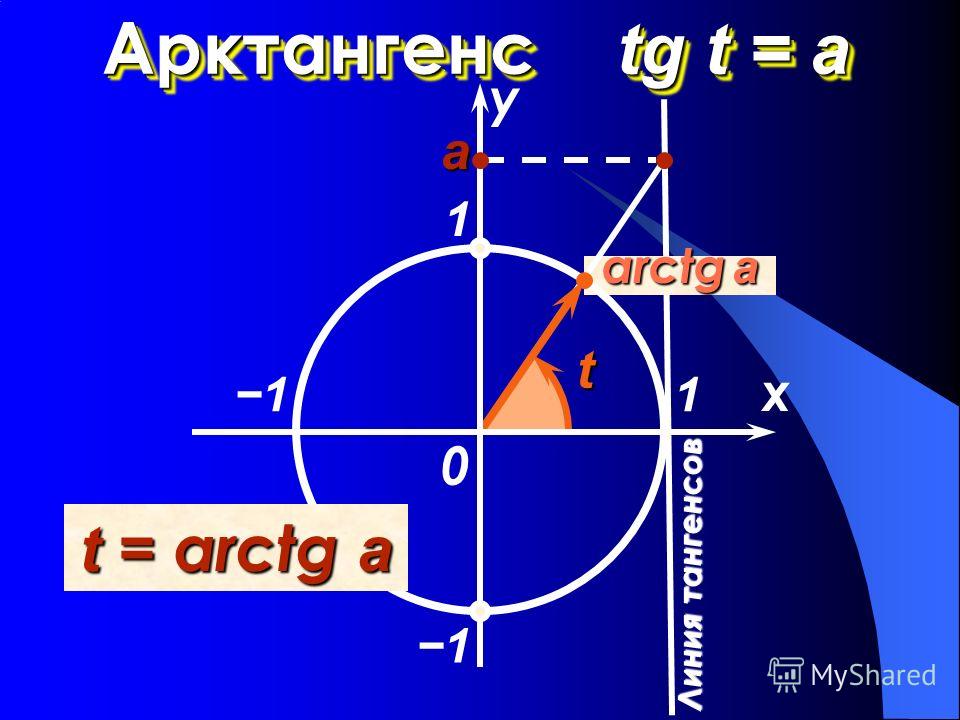 Некоторые математики пишут эти ограниченные триггерные функции и их
перевернутое с заглавной буквы (например, Tan или Tan -1 ).
Однако большинство математиков не следуют этой практике. Этот
веб-сайт не различает заглавные и не заглавные буквы
триггерные функции.
Некоторые математики пишут эти ограниченные триггерные функции и их
перевернутое с заглавной буквы (например, Tan или Tan -1 ).
Однако большинство математиков не следуют этой практике. Этот
веб-сайт не различает заглавные и не заглавные буквы
триггерные функции.
См. также
Обратный тригонометрия, обратная триггерные функции, интервальная запись
Калькулятор арктангенса онлайн — Расчет арктангенса — производная — первообразная
Описание:
Функция arctan позволяет вычислять арктангенс числа.Функция арктангенса — это функция, обратная функции касательной.
Описание:
Функция arctan является обратной функцией касательная функция, Он вычисляет арктангенс числа онлайн .
- Вычисление арктангенса
- Пределы арктангенса Пределы арктангенса существуют в точках `-oo` (минус бесконечность) и` + oo` (плюс бесконечность):
Чтобы вычислить арктангенс числа, просто введите число и примените arctan функция.2) `.
- Функция арктангенса имеет ограничение в `-oo`, которое равно` pi / 2`.
- Функция арктангенса имеет предел в` + oo`, который равен `-pi / 2`.
- `lim_ (x -> — oo) arctan (x) = pi / 2`
- `lim_ (x -> + oo) arctan (x) = — pi / 2`
Функция arctan позволяет вычислять арктангенс числа.
 2)`
2)`Первообразный арктангенс:
Калькулятор первообразных позволяет вычислить первообразную функции арктангенса.2) `
Предельный арктангенс:
Калькулятор пределов позволяет вычислить пределы функции арктангенса.
Предел для arctan (x) равен limit_calculator (`» arctan (x) `)
Арктангенс обратной функции:
Функция , обратная арктангенсу , — это тангенциальная функция, отмеченная как tan.
Графический арктангенс:
Графический калькулятор может построить функцию арктангенса в интервале ее определения.
Свойство арктангенса функции:
Функция арктангенса — это нечетная функция.Расчет онлайн с арктангенсом (арктангенс)
Решения практических задач (Триггер без слез)
Решения практических задач (Триггер без слез)Триггер без слез:
Авторские права 19972020 Стэн Браун, BrownMath.com
Решения для части 1: Введение
1 Найдите эти углы в градусах: (а) π / 6; (б) 2π; (c) 1 (это верно, радианные углы не обязательно дроби или кратные π).Решения :
(а) (π / 6) × (180 / π) = 30
(б) 2π × (180 / π) = 360
(в) 1 × (180 / π) = (180 / π) ≈ 57,3
2 Какое правильное определение острого угла в интервале обозначения?(а) (0, 90) (б) [0, 90]
Ответ : (0, 90) от 0 до 90 градусов за исключением 0 и 90; [0, 90] от 0 до
90 градусов , включая 0 и 90.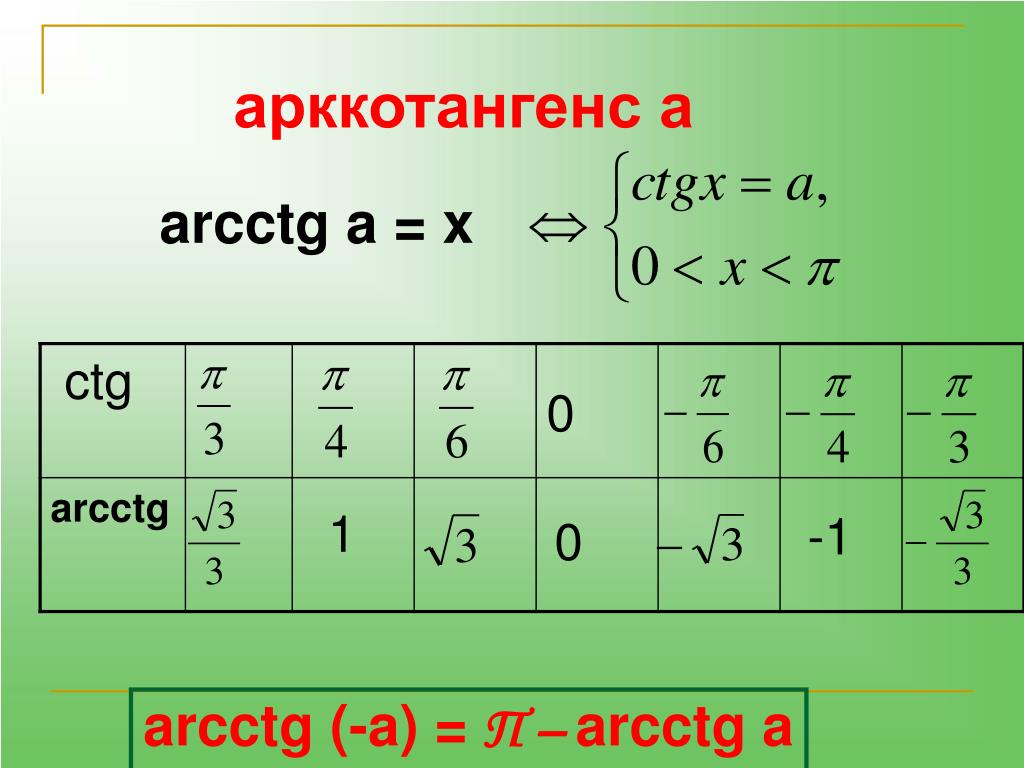 Острые углы
от 0 до 90 исключая , поэтому ответ
(а) (0, 90).
Острые углы
от 0 до 90 исключая , поэтому ответ
(а) (0, 90).
Решение : внутренние углы треугольник всегда должен составлять 180. 80 + 40 = 120, поэтому, чтобы сделать полные 180, третий угол должен быть 60.
4 Треугольник имеет угол 90. Две короткие стороны (рядом с этим угол) равны 5 и 12. Найдите третью сторону.Решение : Подскажите теорему Пифагора!
c = a + b
c = 5 + 12
с = 25 + 144 = 169
c = √169 = 13
5 Найдите эти углы в радианах: (а) 60 (б) 126; (в) 45.По возможности, дайте точный ответ, а не десятичную дробь приближение.
Решения :
(а) 60 + (π / 180) = π / 3.
(б) 126 × (π / 180) ≈ 2,20
(в) 45 × (π / 180) = π / 4
Обратите внимание, что вам не нужно говорить радианы, когда
давая угол в радианах, хотя это было бы неправильно. В этой книге углы в градусах помечены знаком градуса (), поэтому
Я скажу радианы только тогда, когда это необходимо
избежать путаницы.
В этой книге углы в градусах помечены знаком градуса (), поэтому
Я скажу радианы только тогда, когда это необходимо
избежать путаницы.
Ответ : Это было Чучело в фильме Волшебник Оз (1939).И нет, это звучит глупо, но это чушь. Это не может быть верным для любого треугольника , равнобедренного или нет. (Вы понимаете, почему?)
7 На круглом циферблате, цифры которого являются границами каждого квадрант?Ответы : Квадрант I: 12 и 3; Квадрант II: 9 и 12; Квадрант III: 6 и 9; Квадрант IV: 3 и 6.
Решения для части 2: шесть функций
1 Найдите все шесть функций угла 30. Найдите синус, косинус, и тангенс 60. Решение : Во-первых, вам нужна длина горизонтального
сторона.Вы помните теорему Пифагора:
1 + b = 2, откуда вы
получаем b = √3.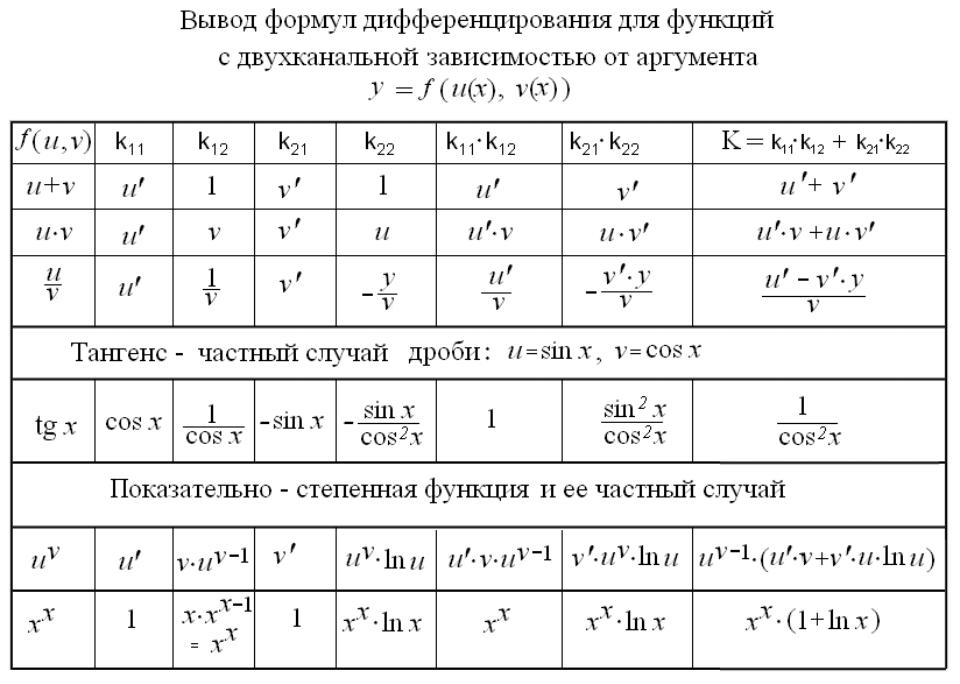 После этого это просто
вопрос запоминания определений. Если вам нужно освежиться,
вы найдете синус и косинус в уравнении 1, касательную в
уравнение 4, а остальные в уравнении 5.
После этого это просто
вопрос запоминания определений. Если вам нужно освежиться,
вы найдете синус и косинус в уравнении 1, касательную в
уравнение 4, а остальные в уравнении 5.
грех 30 = 1/2
cos 30 = √3 / 2
tan 30 = 1 / √3 или √3 / 3
детская кроватка 30 = 1 / (1 / √3) = √3
сек 30 = 1 / (√3 / 2) = 2 / √3 или (2 √3) / 3
csc 30 = 1 / (1/2) = 2
грех 60 = √3 / 2
cos 60 = 1/2
загар 60 = √3 / 1 = √3
Поскольку 60 = 90–30, обратите внимание, что грех 60 = соз 30, соз 60 = грех 30 и загар 60 = детская кроватка 30.
2 Найдите sin A , sin B , tan A и tan B .Решение :
sin A = 3/5 или 0,6
sin B = 4/5 или 0,8
коричневый A = 3/4 или 0,75
загар B = 4/3 ≈ 1,33
Между прочим, A ≈ 36,87, а B ≈ 53,13.
3 A ≈ 53,13. Найдите примерную площадь треугольник. Подсказка: площадь треугольника равна основание × высота /2.
Подсказка: площадь треугольника равна основание × высота /2.Решение : У вас есть основание (5), поэтому вам просто нужна высота. Но sin A = h /3, поэтому h = 3 × sin A . Таким образом, площадь (5 × 3 × sin A ) / 2 ≈ 5,99999.
Решения для части 3: Функции специальных углов
1 (a) Нарисуйте треугольник 45-45-90 с гипотенузой 1. Обозначьте размер каждого угла и точную длину каждой стороны, а не калькулятор приближения. (Подсказка: поскольку два острых угла равны, две короткие стороны должны быть равны.Это и теорема Пифагора достаточно, чтобы вы могли их найти.) (b) Нарисуйте треугольник, все стороны которого равны 1. Если все стороны
равны, все углы должны быть равны. Зная, что они добавляют к
180, введите значение каждого угла. Теперь опустите перпендикуляр
от вершины треугольника до середины противоположной стороны. Ты
теперь есть два треугольника 30-60-90 с гипотенузой 1. Заполните
точные длины коротких сторон этих двух треугольников.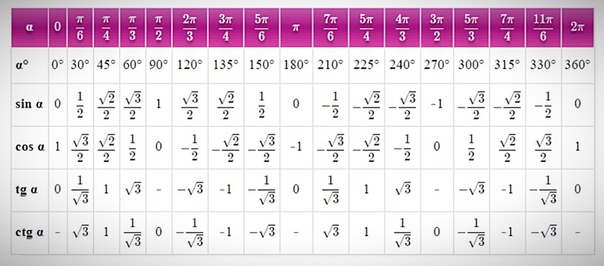
Для решения остальных проблем обратитесь к этим эскизам. Если вам нужно. Дайте точные ответы, а не десятичные дроби.
Решение : Сравните свои наброски с теми, что в глава.
2 Найдите tan 45, cos 45, sin 90, cos 30, грех 30, cos 90.Ответы : загар 45 = 1; cos 45 = 1 / √2 или √2 / 2; грех 90 = 1; cos 30 = √3 / 2; грех 30 = 1/2; cos 90 = 0.
3 Найдите sin (π / 4), cos (π / 6), tan (π / 3).Ответы : sin (π / 4) = √2 / 2 или 1 / √2; cos (π / 6) = √3 / 2; загар (π / 3) = √3
4 Найдите каждый из следующих углов от ключей, предполагая, что все углы составляют от 0 до π / 2 (от 0 до 90) включительно.Дайте каждый ответ в градусах и радианах. sin A = 0; cos B = √3 / 2; sin C = 1/2; sin D = 1; tan E = 1; cos F = 1/2; tan G = 0; загар H = √3; cos I = 1; cos Дж = 0.ответы :
sin A = 0 ⇒ A = 0 или 0 [радиан]
cos B = √3 / 2 ⇒ B = 30 или π / 6
sin C = 1/2 ⇒ C = 30 или π / 6
sin D = 1 ⇒ D = 90 или π / 2
загар E = 1 ⇒ E = 45 или π / 4
cos F = 1/2 ⇒ F = 60 или π / 3
tan G = 0 ⇒ G = 0 или 0 [радианы]
загар H = √3 ⇒ H = 60 или π / 3
cos I = 1 ⇒ I = 0 или 0 [радиан]
cos Дж = 0 ⇒ Дж = 90 или π / 2
5 Найдите сек 60 и детскую кроватку 30.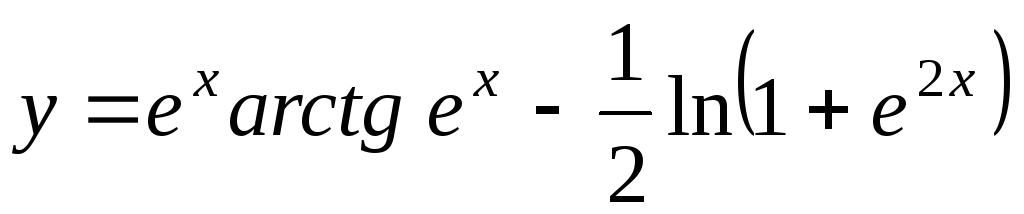 Подсказка: помните, как
секанс и котангенс определяются в терминах
большие три функции: синус, косинус и тангенс.
Подсказка: помните, как
секанс и котангенс определяются в терминах
большие три функции: синус, косинус и тангенс.Решения : сек 60 = 1 / (cos 60) = 1 / (1/2) ⇒ сек 60 = 2
детская кроватка 30 = 1 / (загар 30) = 1 / (√3 / 3) = 3 / √3 = √3 ⇒ детская кроватка 30 = √3
Вы также можете выполнить второй, используя уравнение 6:
детская кроватка 30 = загар (90-30) = загар 60 = √3
6 Найдите sin 120, cos 120 и tan 120.Решение:
грех 120 = грех (180 — 120) = √3 / 2.
cos 120 = −cos (180 — 120) = −1/2.
А как насчет касательной? У вас нет правила о добавках для него, но у вас есть другой способ найти ответ:
загар 120 = грех 120 / соз 120 = (√3 / 2) / (−1/2) = −√3
7 Несмотря на то, что вы всегда можете получить дополнительный угол от синуса и косинуса, это экономит время, чтобы иметь правило для дополнения касательной. Решение последних проблем предположил, что это за правило.
Доказательство: загар (180 — A ) = −tan А .
Проба:
желто-коричневый (180- A ) = sin (180 — A ) / cos (180 — A )
желто-коричневый (180- A ) = sin A / (−cos A )
желто-коричневый (180- A ) = −sin A / cos A
желто-коричневый (180- A ) = −tan A QED
8 Найдите загар 150.Решение: загар 150 = −tan (180 — 150) = −tan 30 = −√3 / 3
Решения для части 4: Решение треугольников
1 У вас есть прямоугольный треугольник ( C = 90) с короткие стороны a = 88 и b = 37.Решите треугольник.Всегда начинайте с эскиза. На скетче справа видно прочь, что это случай с SAS, или сторона-угол-сторона. Чтобы получить третью сторону, вам нужен закон косинусов, уравнение 31.
c = a + b — 2 a b × cos C
с = 37 + 88 — 2 × 37 × 88 × cos 90
Обратите внимание на то, что, когда включенный угол C равен 90,
cos C = 0, и вы только что получили пифагорейский
Теорема.
c = 37 + 88
c = √37 + 88
c ≈ 95,5
Чтобы найти два угла, вы можете использовать Закон синуса, но почему бы не взять Преимущество прямого угла и использования тангенса?
желто-коричневый A = 37/88 ⇒ A ≈ 22,8
Конечно, загар B = 88/37, но вы также знаете, что
A + B = 90 ⇒ B = 90 — A ⇒ B ≈ 67.2
2 (Нарисуйте эту проблему по мере ее чтения.) В государственном парке река течет практически прямо к 1800 м. Вы хотите построить монорельс из A , один конец этот участок до точки C на дальнем берегу. Вы также хотите построить пешеходный мост от B , на другом конце этого участка реки, до той же точки C на дальнем берегу. На A угол между линиями обзора к B и C — 67.При B угол между вашим прицелом линии на A и C — 38.Какой длины должны быть монорельс и пешеходный мост?
Бонусный вопрос: если река имеет одинаковую ширину на всем протяжении протянуть от A до B , насколько он широкий?
На эскизе b — монорельс, a — подножка. мост, а w ширина реки. Поскольку вы знаете два
углы и включенная сторона, это случай ASA.Хотя ты
не особо заботьтесь об угле C , вы должны его найти
так что вы можете использовать закон синусов, чтобы получить стороны a и b :
мост, а w ширина реки. Поскольку вы знаете два
углы и включенная сторона, это случай ASA.Хотя ты
не особо заботьтесь об угле C , вы должны его найти
так что вы можете использовать закон синусов, чтобы получить стороны a и b :
С = 180 — 67 — 38 = 75
Очевидно, когда я смотрел на углы A и B Я не очень их оценил! Но это хорошо, набросок достаточно близок, чтобы быть полезным.
Какова длина пешеходного моста? От Закон Синуса,
a / sin A = c / sin C ⇒ a = c sin A / sin C
= 1800 × грех 67 / грех 75
Пешеходный мост: a ≈ 1715 м
Какова длина монорельса? От Закон Синуса,
b / sin B = c / sin C ⇒ b = c sin B / sin C
б = 1800 × грех 38 / грех 75
Монорельс: b ≈ 1147 м
Насколько широка река?
w = b sin A
w ≈ 1147 sin 67
Ширина реки: w ≈ 1056 м
3 Найдите другие элементы треугольника с B = 117, a = 16 см и b = 25 см.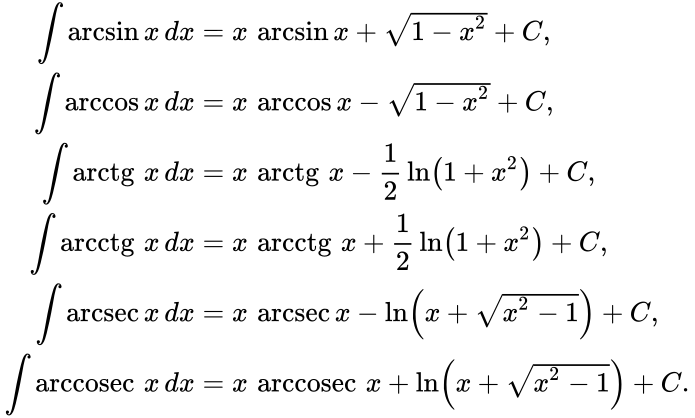
Это случай SSA (или ASS); обратитесь к таблица возможностей для SSA. Эта проблема принадлежит строке 1, столбцу 2: противоположная сторона длиннее, чем соседняя сторона, и известный угол> 90. Итак, есть одно и только одно решение.
Вы можете использовать закон синусов, чтобы найти угол A :
(sin A ) / a = (sin B ) / b
sin A = ( a / b ) sin B
sin A = (16/25) sin 117 ≈ 0.57024
A ≈ 34,8
Найдите третий угол, вычтя:
С = 180- А — В
C ≈ 180 — 34,8 — 117
C ≈ 28,2
Наконец, используйте закон синуса, чтобы найти сторону с :
c / sin C = b / sin B
c = b sin C / sin B
c ≈ 25 sin 28.2 / грех 117
c ≈ 13,3 см
4 Подставка под столешницу очень современного вида представляет собой треугольную форму со сторонами 6 дюймов, 9 дюймов и 12 дюймов.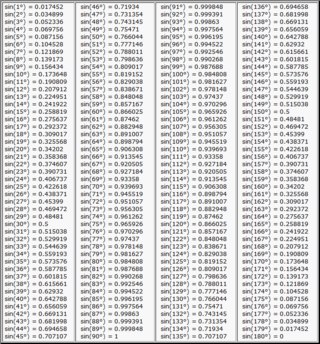 Какие
три угла?
Какие
три угла?Это случай SSS. Сначала используйте Закон косинусов для определения угла A:
cos A = ( b + c — a ) / 2 b c
cos A = (9 + 12-6) / (2 × 9 × 12) = 0,875
A ≈ 29,0
Затем используйте закон синусов, чтобы найти угол B :
(sin B ) / b = (sin A ) / a ⇒ sin B = ( b / a ) sin A
sin B ≈ (9/6) sin 29.0 ≈ 0,72618
B ≈ 46,6
Наконец, вычтите два угла из 180, чтобы найти третий угол:
C = 180- A — B
C ≈ 180 — 29,0 — 46,6
C ≈ 104,5
Кстати, это не опечатка. A и B оба оказались округленными, но я использовал неокругленные значения, чтобы найти С . Вы никогда не должны использовать округленные числа в дальнейшем расчеты.
5После того, как вы покрасили спальню, у вас достаточно краской осталось покрыть 25 футов.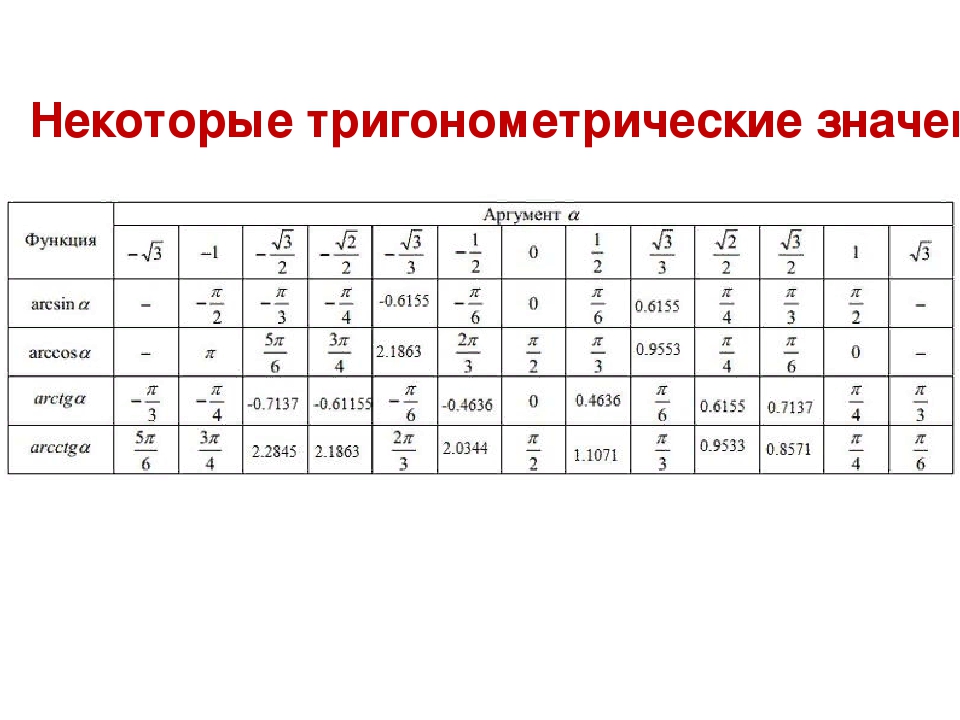 Вы решаете нарисовать треугольник
на стене другой комнаты, как акцент. Два угла должны быть
30 и 40. Найдите третий угол и длины
с трех сторон.
Вы решаете нарисовать треугольник
на стене другой комнаты, как акцент. Два угла должны быть
30 и 40. Найдите третий угол и длины
с трех сторон.Третий угол 180-30-40, так что С = 110. Сделайте свой набросок, используя эти три угла. (Я сделал это без Измерение углов, так что это не идеально. Но зарисовки не обязательно быть идеальным, просто достаточно близким.)
Найдите сторону c с помощью уравнения 32:
с = √2 площадь × sin C / (sin A sin B )
с = √2 × 25 × sin 110 / (sin 30 sin 40)
c ≈ 12,1 фут
Тогда закон синуса дает вам другое с двух сторон:
a = c sin A / sin C
a ≈ 12,1 sin 30 / sin 110
a ≈ 6.4 фута
и
b = c sin B / sin C
b ≈ 12,1 sin 40 / sin 110
b ≈ 8,3 фут
6 Вы проезжаете 6,0 миль по прямому шоссе, затем съезжаете.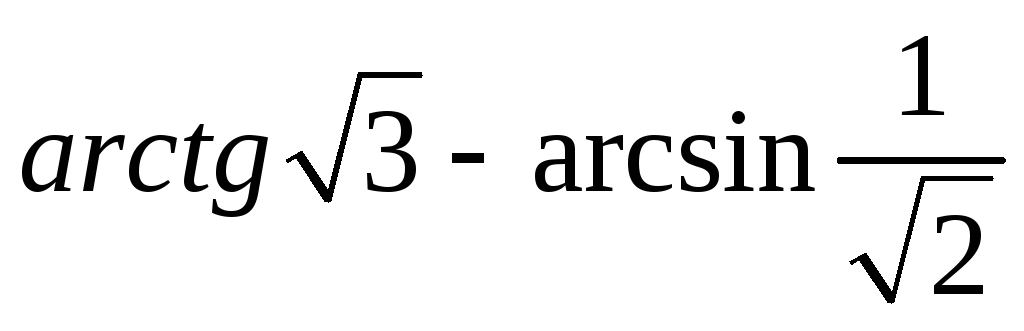 Поворот направо, но угла не замечаешь.
Поворот направо, но угла не замечаешь.Вы едете по прямой проселочной дороге. Пройдя 9,8 миль по проселочной дороге, вы повернете 135 на правильно, на третьей дороге. (Если вы визуализируете это сверху, изменение направления на 135 соответствует углу 180 — 135 = 45 в треугольнике.)
Если предположить, что дорога продолжается в том же направлении, как далеко нужно ехать, чтобы добраться до отправной точки?
Это сложный набросок, потому что вы не знаете угол первого поворота. Но описание дает вам две стороны и невключенный угол; это проблемный случай SSA. Вы не знаете, где именно сторона c будет соответствовать стороне a . Если быть более точным, вы даже не знаю , встретятся ли .
Могут ли они встретиться? Ссылаясь на таблица возможностей в SSA, мы видим, что были в третьем ряду, первом столбце: соседние сторона (9.8) длиннее противоположной стороны (6.0), и известный угол (45) <90. Вычислить
h = b sin A
h = 9,8 sin 45 ≈
6.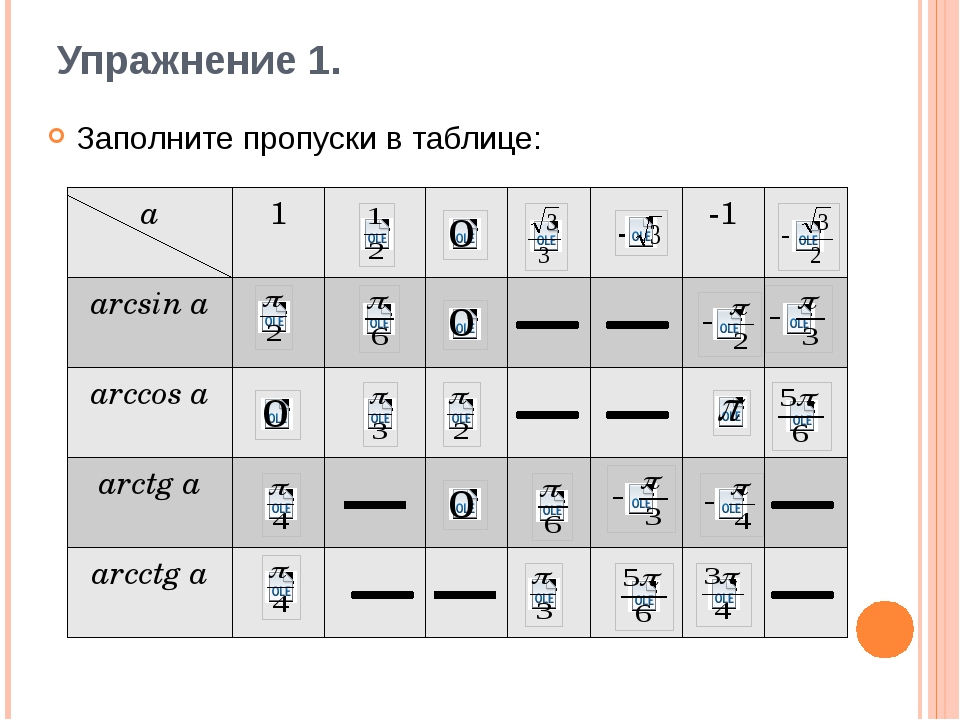 9 миль
9 миль
Что это значит? Кратчайшее расстояние от точки C до стороны c — это отрезок, который соответствует сторона c под прямым углом. Другими словами, чтобы получить от точки C к стороне c , кратчайшее возможное расстояние 6.9 миль. Но сторона у всего 6,0 миль в длину, так что она может никогда не встречал стороны c .
Эта проблема не имеет решения.
Вы выкладываете треугольную грядку для своего сада. Две стороны 40 м и 60 м, а угол между ними равен 22. Какова длина третьей стороны и какие две другие? углы?Вы знаете две стороны и угол между ними. Вы можете использовать Закон косинусов для получения третьей стороны:
a = b + c — 2 b c × cos A
a = 60 + 40 — 2 × 60 × 40 × cos 22
c ≈ √749.52 ⇒ c ≈ 27,4 м
Далее, для угла B можно использовать Закон синуса:
(sin B ) / b = (sin A ) / a ⇒ sin B = (б / а) sin A
sin B ≈ (60 / 27,4) sin 22 ≈ 0,82099
Ваш калькулятор дает около 55,2 как угол, синус которого равен
0. 82099, но это выглядит не так
с эскиза. Очевидно, что угол B должен быть тупым углом, так что помните
что грех (180 — х ) = грех х ,
и вы вычитаете 180 — 55.2, чтобы получить
82099, но это выглядит не так
с эскиза. Очевидно, что угол B должен быть тупым углом, так что помните
что грех (180 — х ) = грех х ,
и вы вычитаете 180 — 55.2, чтобы получить
B ≈ 124,8
Видите, насколько важен эскиз? Конечно твой скетч наверное не совсем точен, поэтому вы относитесь к нему как к способу указать что что-то может быть неправильным, но тогда вы ищите способ подтвердить это. В этом случае у вас есть два способа подтвердить it:
- Вы можете использовать Закон косинусов, который автоматически
учитывает тупые углы:
cos B = ( a + c — b ) / (2 a c )
cos B ≈ (27.4 + 40 — 60) / (2 × 27,4 × 40)
cos B ≈ −0,57095 ⇒ B ≈ 124,8
- Или вы можете вычислить угол C (ниже), а затем вспомнить этот угол C должен быть < B , потому что сторона c — < b . Если вы сделали C тупой, 180 — 33,2 = 146,8, было бы
> B независимо от того, является ли B острым или тупым.
 Так C должен быть <90 и B должен быть
> 90.
Так C должен быть <90 и B должен быть
> 90.
Теперь поверните на угол C:
(sin C ) / c = (sin A ) / a ⇒ sin C = (c / a) sin A
sin C ≈ (40 / 27,4) sin 22 ≈ 0,54732
C ≈ 33,2
Решения для Части 5: Функции под любым углом
1 В каком квадранте находится угол -868? Как насчет 42 радиана? Каковы знаки их синусов, косинусов и касательных?Решение: Ваша задача всегда — изгнать кратные 360 или 2π, чтобы вы оставались с положительным углом от 0 до 360 (от 0 до 2π).
−868 = −1080 + 212. И 212 находится между 180 и 270, так что −868 встречается в Q III.
42 радиана составляет около 13,37π, или 12π + 1,37π. 1,37π, очевидно, находится между π и 3π / 2 (1.5π), поэтому 42 (радианы) находится в III квартале.
В третьем квартале x и y оба отрицательны. Следовательно
В Q III синус и косинус отрицательны, а тангенс положительна.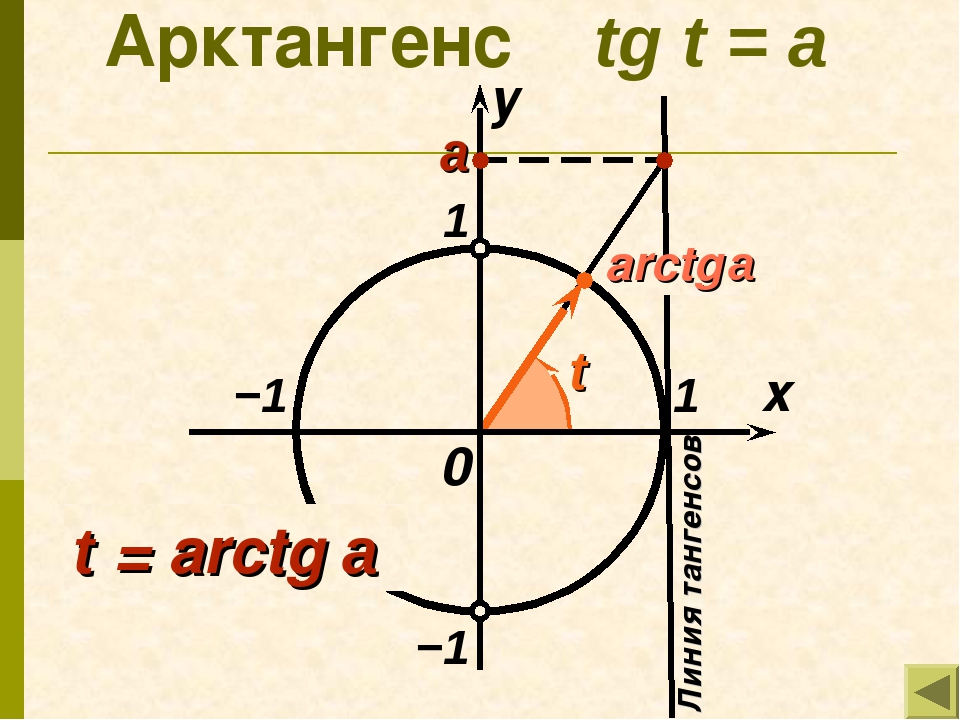
Решение: (a) 700 = 360 + 340, поэтому грех 700 = грех 340. 340 в Q IV, где y отрицательно; следовательно, синус отрицательный. Базовый угол равен 20, поэтому грех 700 = −sin 20.
(б) 780 = 720 + 60, поэтому загар 780 = загар 60.
(в) −390,5 ≈ −124,3π, или −126π + 1,7π; следовательно cos (-390,5) ≈ cos 1,7π. Угол 1,7π радиан находится между 1,5π и 2π, поэтому Q IV, где x положительно и, следовательно, косинус равен положительный.Базовый угол составляет около 2π — 1,7π ≈ 0,3π или 0,94, поэтому cos (-390,5) ≈ cos 0,94.
3 Перепишите как функцию всего A : (а) cos (720 — A ) (б) грех (43π + A ) Решение: (a) 720 делится на 360, поэтому
cos (720 — A ) = cos (- A ). Но cos (- A ) = cos A , и поэтому
cos (720 — A ) = cos A .
Но cos (- A ) = cos A , и поэтому
cos (720 — A ) = cos A .
(б) sin (43π + A ) = грех (42π + π + A ) = sin (π + A ).sin (π + A ) = −sin A , поэтому sin (43π + A ) = −sin A .
Решения для части 6: Квадратные идентичности
1 Если sin A = 3/4, найдите cos A .Решение :
sin² A + cos² A = 1
cos² A = 1 — sin² A = 1 — (3/4) = 1 — 9/16
cos² A = 7/16
cos A = √7 / 16 ⇒ cos A = √7 / 4 или −√7 / 4
Вы помните знак? Как только x = 9 имеет два решения, 3 и −3, поэтому любое уравнение в cos² A имеет два решения.
Это имеет смысл с точки зрения функций. Есть два
углы в интервале [0, 2π) или [0, 360)
где sin A = 3/4, один острый и один тупой. В
острый имеет положительный косинус, а тупой — отрицательный
косинус.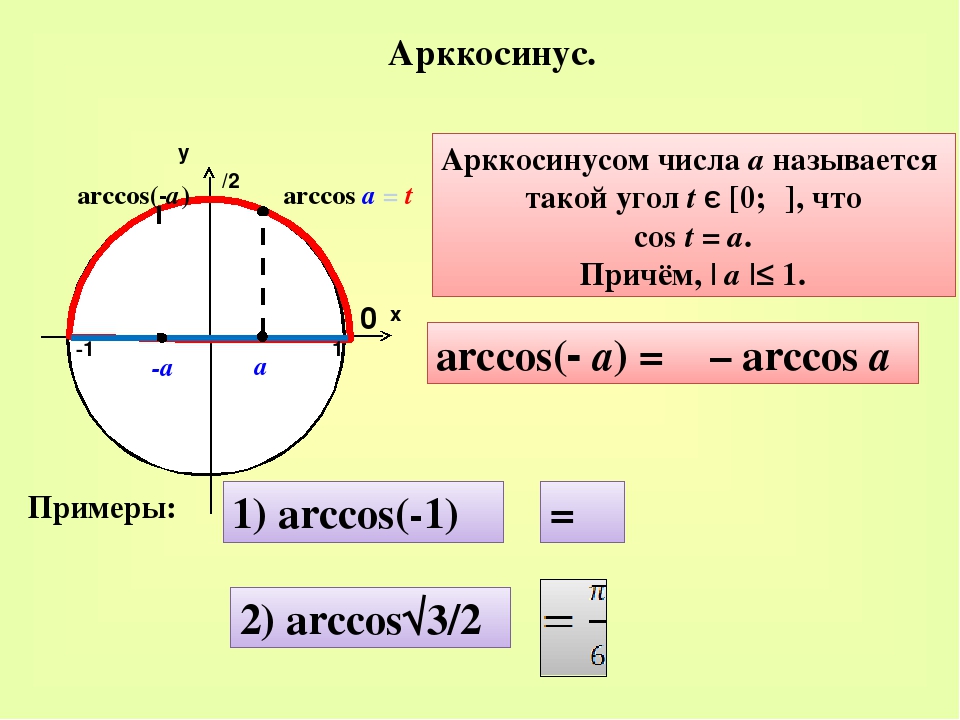
Решение : Поскольку эта глава посвящена в квадрате личности, вы можете быть уверены, что она существует который соединяет загар x и sec x .Но предположим, вы встретили это проблема в другом контексте?
Ну, вы знаете два тождества, в которых используется функция касательной. Определение tan B = (sin B ) / cos B , не много ли вам добра, потому что в нем смешаны синус и косинус вместе. Вы плохо помните квадратную идентичность (если вы как и я, он тусклый), но вы также знаете, что можете воссоздать его легко, с одного квадратная идентичность, которую невозможно забыть:
sin² B + cos² B = 1
У вас есть sin² B , который станет tan² B , если вы разделите обе стороны на cos² B .
(sin² B ) / cos² B + (cos² B ) / cos² B = 1 / cos² B
tan² B + 1 = sec² B
Успех! У вас есть личность, которая связывает касательную и
секущие функции. Теперь можно переходить к решению проблемы.
Теперь можно переходить к решению проблемы.
(−2√2) + 1 = сек² B
сек² B = (4 × 2) + 1 = 9
сек B = 3
Знак вам нужен, потому что оба ( x ) и (- x ) равны x .Но делает это имеет смысл с точки зрения триггера? Да, потому что касательная отрицательна в Q II и Q IV, а секущая, имеющая то же знак как косинус, 1 по косинусу положителен в Q IV, но отрицательный в Q II.
3 загар C = √15. Найдите cos C .Решение : Подождите, что? У тебя нет тождество, соединяющее тангенс и косинус. Но у вас у есть один соединяя касательную и секанс, и вы знаете, что секанс на 1 больше косинус, так что вы тоже можете сделать это.
Начните с квадрата идентичности из предыдущей задачи:
tan² C + 1 = sec² C
(√15) + 1 = 15 + 1 = 16 ⇒ сек² C = 16
сек C = 4 ⇒ cos C = 1/4
4 tan D = √15, Найти sin D .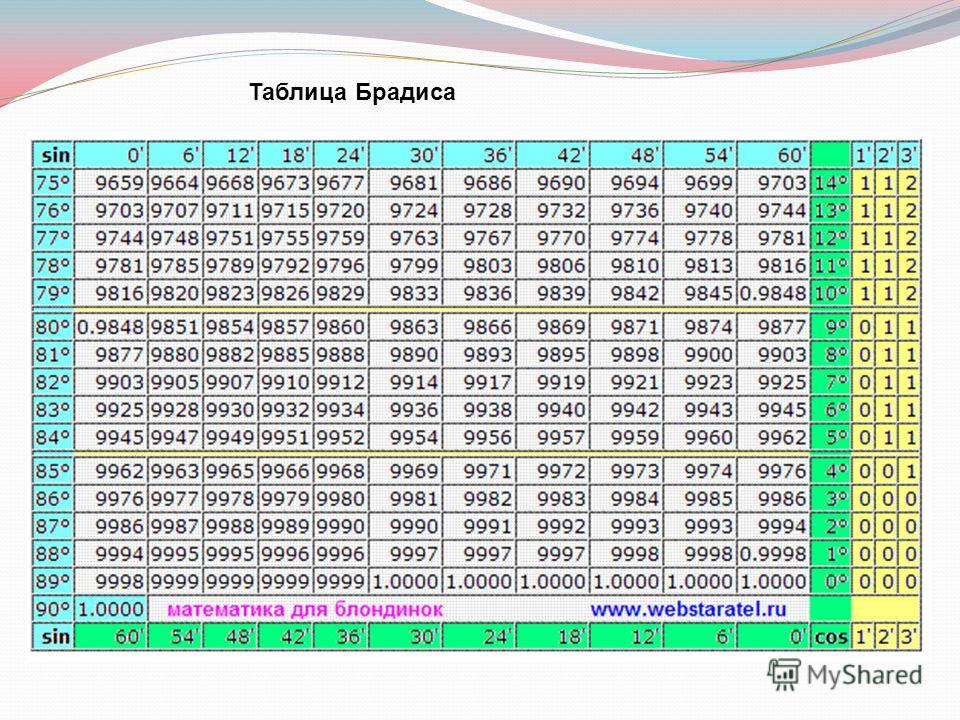
Решение : Хорошо, в предыдущей задаче вы получили касательная к косинусу. Но вы уже знаете, как перейти от косинуса к sine, так что у вас есть еще одно звено в цепочке.
tan² D + 1 = sec² D
сек² D = (√15) + 1 = 16
сек D = 4 ⇒ cos D = 1/4
sin² D + cos² D = 1
sin² D = 1 — cos² D = 1 — (1/4) = 1 — 1/16 = 15/16
sin D = √15 / 4
5 Докажите: sin² x = tan² x / (tan² x + 1)Предполагается, что x ≠ π / 2 + k π, для целого числа к или 90 + 180 к , если вы предпочитаю, потому что тангенс для этих углов не определен.
Проба :
желто-коричневый x = коричневый x
загар x cos x = загар x cos x
sin x = коричневый x / сек x
sin² x = tan² x / сек² x
But tan² x + 1 = sec² x , поэтому замена у вас
sin² x = tan² x / (tan² x + 1) QED
Возможны многие другие доказательства.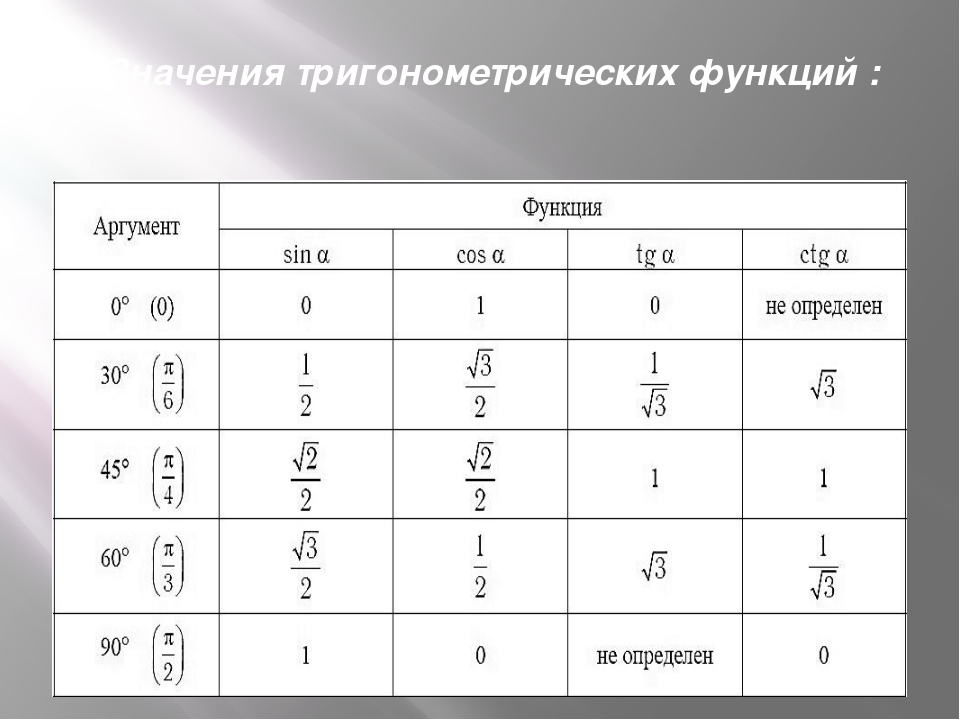 Например, вы можете заменить
tan² x с sin² x / cos² x в
личность вас попросили подтвердить, а затем упростить дробь.
Пока каждый шаг в вашем доказательстве действителен как в обратном, так и в обратном направлении.
вперед, ваше доказательство в порядке.
Например, вы можете заменить
tan² x с sin² x / cos² x в
личность вас попросили подтвердить, а затем упростить дробь.
Пока каждый шаг в вашем доказательстве действителен как в обратном, так и в обратном направлении.
вперед, ваше доказательство в порядке.
Если ваше доказательство начинается с очевидной идентичности, а затем работает вперед к личности, которую мы попросили подтвердить, как и вышеприведенное доказательство, тогда имеет значение только то, что все шаги действительны в этом форварде направление.
Решения для части 7: формулы суммы и разности
1 Точно найдите sin (−15).Решение: Начать с −15 = 30-45
грех (-15) = грех (30-45)
грех (-15) = грех 30 cos 45 — соз 30 грех 45
грех (-15) = (1/2) (√2 / 2) — (√3 / 2) (√2 / 2) = √2 / 4 — √6 / 4
грех (-15) = (√2 — √6) / 4
Альтернативное решение: Вы также можете сделать это, используя 45-60:
грех (-15) = грех (45-60)
грех (-15) = грех 45 cos 60 — соз 45 грех 60
грех (-15) = (√2 / 2) (1/2) — (√2 / 2) (√3 / 2) = √2 / 4 — √6 / 4 = (√2 — √6) / 4
2 Найдите загар 105 точно.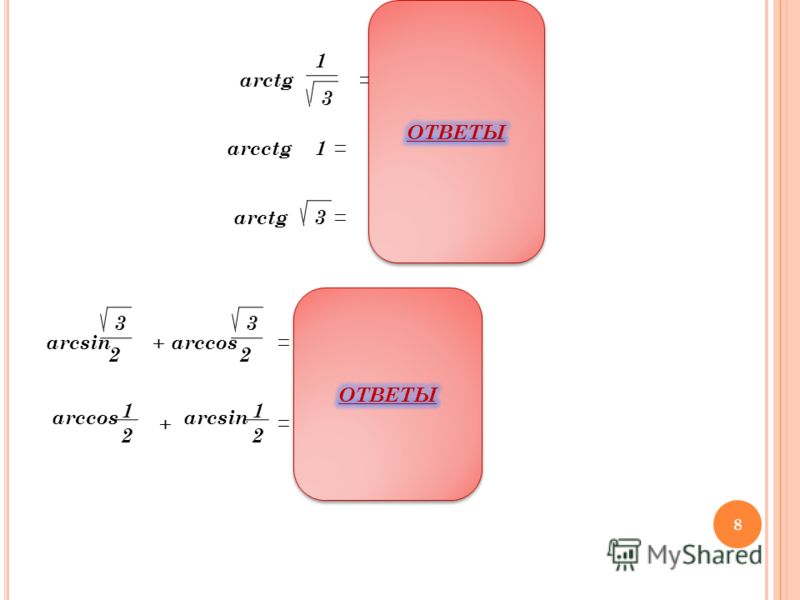
Решение: 105 = 60 + 45
загар 105 = загар (60 + 45)
загар 105 = (загар 60 + загар 45) / (1 — загар 60 загар 45)
загар 105 = (√3 + 1) / (1 — (√3) (1)) = (√3 + 1) / (1 — √3)
Умножить верхнюю и нижнюю на 1 + √3, чтобы получить рационализировать знаменатель:
загар 105 = (√3 + 1) / ((1 — √3) (1 + √3))
загар 105 = (3 + 2√3 + 1) / (1-3) = (4 + 2√3) / (- 2) = −2 — √3
3 Докажите: cos 2 A = 2 cos² A — 1. (Подсказка: 2 A = A + A .)Проба:
cos 2 A = cos ( A + A )
cos 2 A = cos A cos A — sin A sin A
cos 2 A = cos² A — sin² A
Но sin² A = 1 — cos² A
cos 2 A = cos² A — (1 — cos² A ) = cos² A — 1 + cos² A
cos 2 A = 2 cos² A — 1 QED
4 Докажите эти формулы из уравнения 22, используя формулы для функций суммы и разности.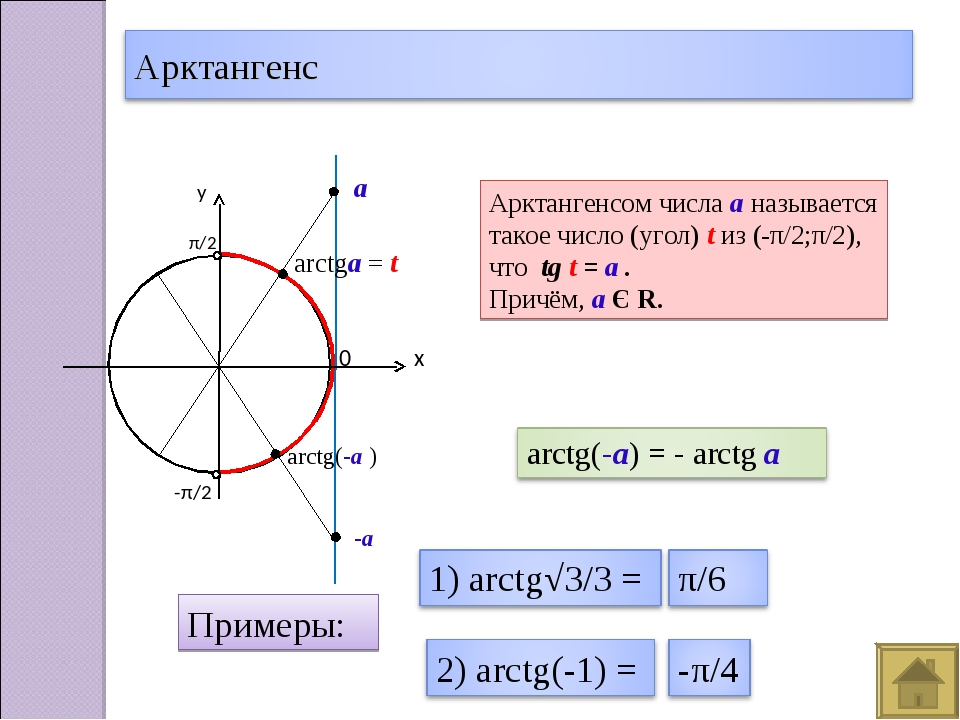
(a) cos (- A ) = cos A (Я сделал за вас первый шаг.)
cos (- A ) = cos (0- А )
cos (- A ) = cos 0 cos A + sin 0 sin A
cos (- A ) = 1 cos A + 0 sin A
cos (- A ) = cos A QED
(б) загар (π + A ) = загар A
загар (π + A ) = (загар π + загар A ) / (1 — загар π загар A )
загар (π + A ) = (0 + загар A ) / (1-0 загар A )
загар (π + A ) = (загар A ) / 1
загар (π + A ) = желто-коричневый A QED
(c) sin (π — A ) = sin A
грех (π — A ) = sin π cos A — cos π sin A
грех (π — A ) = 0 cos A — (−1) sin A
грех (π — A ) = грех A QED
Решения для части 8: формулы двойного и половинного угла
1 Используйте формулы половинного угла, чтобы найти sin 90 и cos 90.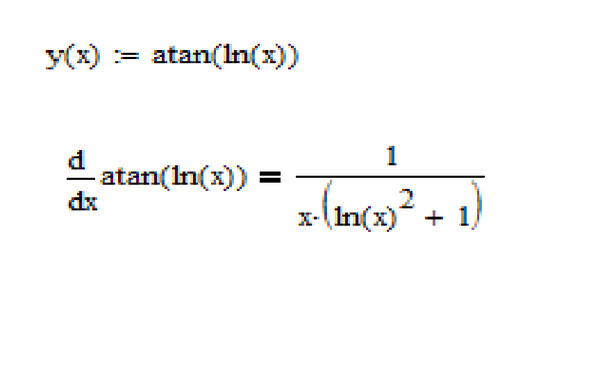 Конечно, вы их уже знаете; эта проблема
просто для практики в работе с формулами и легкими числами.
Конечно, вы их уже знаете; эта проблема
просто для практики в работе с формулами и легкими числами.Решение: : 90 — это половина 180. Синус и косинус равны положительный или ноль на 90, поэтому знаки в формулах можно рассматривать как положительный.
грех (180/2) = √ (1 — cos 180) / 2 = √ (1 — (−1)) / 2 = √2 / 2
грех 90 = 1
cos (180/2) = √ (1 + соз 180) / 2 = √ (1 + (−1)) / 2 = √0 / 2
cos 90 = 0
Почему я не просил вас сделать то же самое для загар 90?
2 Воспользуйтесь формулами двойного угла, чтобы найти sin 120, cos 120, а tan 120 точно.Опять же ты уже знать это; Вы только начинаете знакомиться с формулами.Решение: 120 — это двойное 60. sin 60 = √3 / 2, cos 60 = 1/2 и загар 60 = √3.
грех (260) = 2 sin 60 cos 60 = 2 (√3 / 2) (1/2)
грех 120 = (√3) / 2
cos (260) = 2 cos² 60 — 1 = 2 × (1/2) — 1 = (1/2) — 1
cos 120 = −1/2
загар (260) = 2 загар 60 / (1 — загар² 60) = 2 √3 / (1 — (√3)) = 2 √3 / (1-3) = 2 √3 / (−2)
загар 120 = −√3
Альтернативное решение: Вы также можете разделить:
загар 120 = грех 120 / соз 120 = (√3 / 2) / (−1/2) = −√3
3 3 A = 2 A + A . Используйте формулы двойного угла вместе с
формулы для синуса или косинуса суммы, чтобы найти
формулы для sin 3 A только в терминах sin A ,
и cos 3 A только в терминах cos A .
Используйте формулы двойного угла вместе с
формулы для синуса или косинуса суммы, чтобы найти
формулы для sin 3 A только в терминах sin A ,
и cos 3 A только в терминах cos A .(На самом деле это было сделано позднее раздел, используя другой метод.)
Решение: Сначала синус:
sin (2 A + A ) = sin 2 A cos A + cos 2 A sin A
sin 3 A = (2 sin A cos A ) cos A + (1-2 sin² A ) sin A
sin 3 A = 2 sin A cos² A + sin A — 2 sin³ A
sin 3 A = 2 sin A (1 — sin² A ) + sin A — 2 sin³ A
sin 3 A = 2 sin A — 2 sin³ A + sin A — 2 sin³ A
sin 3 A = 3 sin A — 4 sin³ A , или (3 — 4 sin² A ) sin A
Теперь косинус:
cos (2 A + A ) = cos 2 A cos A — sin 2 A sin A
cos 3 A = (2 cos² A — 1) cos A — (2 sin A cos A ) sin A
cos 3 A = 2 cos³ A — cos A — 2 sin² A cos A
cos 3 A = 2 cos³ A — cos A — 2 (1 — cos² A ) cos A
cos 3 A = 2 cos³ A — cos A — 2 cos A + 2 cos³ A
cos 3 A = 4 cos³ A — 3 cos A , или (4 cos² A — 3) cos A
4 Учитывая грех 3 A = (3 — 4 sin² A ) sin A и cos 3 A = (4 cos² A — 3) cos A , найти tan 3 A только с точки зрения tan A .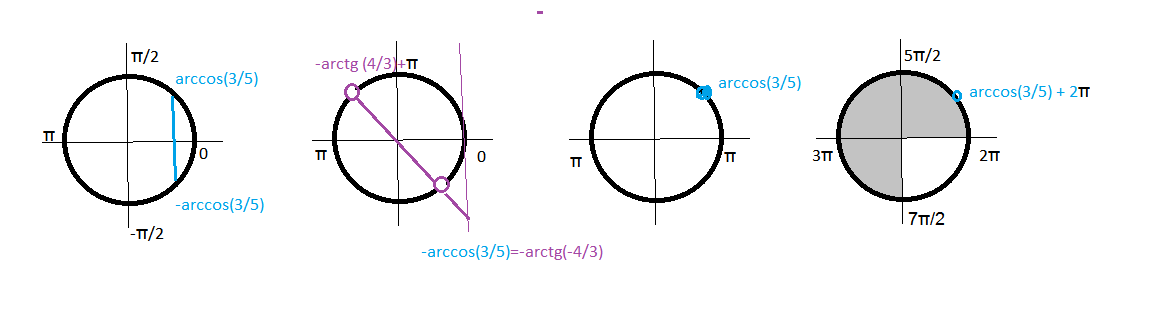 Проверьте себя, вычислив загар (2 A + A ).
Проверьте себя, вычислив загар (2 A + A ).Решение:
коричневый 3 A = sin 3 A / cos 3 A
коричневый 3 A = ((3 — 4 sin² A ) sin A ) / ((4 cos² A — 3) cos A )
коричневый 3 A = (sin A / cos A ) (3 — 4 sin² A ) / (4 cos² A — 3)
коричневый 3 A = tan A (3 — 4 sin² A ) / (4 cos² A — 3)
Разделите верх и низ на cos² A .Это по крайней мере избавляет of sin² A и cos² A , хотя он вводит секущие функции. (Вы помните, что 1 / cos A = сек A , верно?)
коричневый 3 A = желто-коричневый A (3 сек² A — 4 tan² A ) / (4 — 3 сек² A )
Возможно, это выглядит не лучше, но раньше вам пришлось
избавиться от двух нежелательных функций; теперь у вас есть только один нежелательный
функция, даже если это происходит дважды. И его sec² A .
Разве нет какого-то
Пифагорейская идентичность с участием
sec² A ? Да, есть! sin² A +
cos² A = 1 ⇒ tan² A +1 =
сек² A .
И его sec² A .
Разве нет какого-то
Пифагорейская идентичность с участием
sec² A ? Да, есть! sin² A +
cos² A = 1 ⇒ tan² A +1 =
сек² A .
коричневый 3 A = желто-коричневый A (3 (tan² A + 1) — 4 tan² A ) / (4 — 3 (tan² A + 1))
коричневый 3 A = tan A (3 tan² A + 3-4 tan² A ) / (4–3 tan² A — 3)
коричневый 3 A = желто-коричневый A (3 — желтовато-коричневый² A ) / (1 — 3 желтовато-коричневый² A )
Чек:
коричневый (2 A + A ) = (желто-коричневый 2 A + коричневый A ) / (1 — коричневый 2 A желто-коричневый A )
Из уравнения 60, tan 2 A = 2 желто-коричневый A / (1 — коричневый² A ).
коричневый 3 A = (2 желто-коричневый A / (1 — коричневый² A ) + коричневый A ) / (1 — (2 желтовато-коричневый A / (1 — коричневый² A )) коричневый A )
Ну вот и бардак! Очистите это, умножив вершину и
снизу по (1 — tan² A ).
коричневый 3 A = (2 желтых A + (1 — желтовато-коричневый² A ) желто-коричневый A ) / ((1 — желтовато-коричневый² A ) — 2 желто-коричневый A желто-коричневый A )
коричневый 3 A = (3 желтых A — желто-коричневых³ A ) / (1 — 3 желтых² A )
Вынести за скобки загар A из верхней части фракции, и он такой же, как и в первом методе:
коричневый 3 A = желто-коричневый A (3 — желтовато-коричневый² A ) / (1 — 3 желтовато-коричневый² A )
5 Точно найдите синус, косинус и тангенс числа π / 8.Решение: π / 8 (22) составляет половину от π / 4 (45), поэтому вам нужны формулы половинного угла. А π / 8 находится в квадранте I, поэтому все значения функции будут положительными.
грех π / 8 = √ (1 — cos π / 4) / 2
грех π / 8 = √ (1 — √2 / 2) / 2 = √ (2 — √2) / 4 = () √2 — √2
Это выражение содержит вложенных радикалов .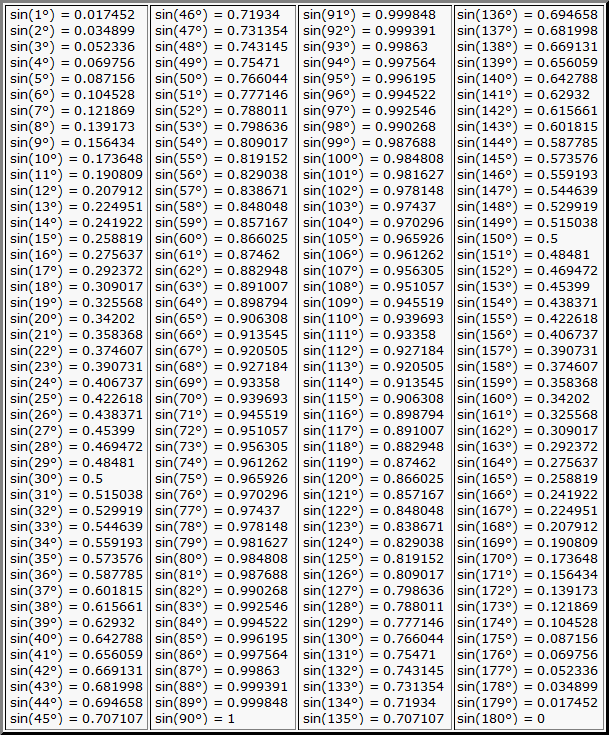 Хотя некоторые вложенные радикалы могут быть денестированы, следуя
техника в Denesting Radicals (или Unnesting Radicals), эта
к сожалению, нет.
Хотя некоторые вложенные радикалы могут быть денестированы, следуя
техника в Denesting Radicals (или Unnesting Radicals), эта
к сожалению, нет.
cos π / 8 = √ (1 + cos π / 4) / 2
cos π / 8 = √ (1 + √2 / 2) / 2 = √ (2 + √2) / 4 = () √2 + √2
Теперь перейдем к касательной.Вы можете использовать формула полуугла, или просто разделите синус на косинус.
загар π / 8 = (грех π / 8) / (соз π / 8)
загар π / 8 = √2 — √2 / √2 + √2
Этот можно денвертировать , если умножить вершину и снизу на √2 — √2. Ты обычно делаешь это так или иначе, чтобы рационализировать знаменатель, но это хороший бонус, который происходит, чтобы очистить числитель.
тангенциальный π / 8 = √ (2 — √2) (2 — √2) / √ (2 + √2) (2 — √2)
загар π / 8 = (2 — √2) / √ (4 — 2) = (2 — √2) / √2 = √2 — 1
Решения для Части 9: Обратные функции
1 Возможные выходные значения Arcsin x включают π / 2, но возможные выходные значения Arctan x делают нет. Почему Arctan x никогда не может равняться −π / 2 или
π / 2?
Почему Arctan x никогда не может равняться −π / 2 или
π / 2?Решение : Arctan x — это угол, тангенс которого равен x , поэтому возможные значения Arctan x — это углы в Q IV и Q I, касательные к которым можно брать. Но tan −π / 2 и tan π / 2 не существует, поэтому они не являются возможными значениями Арктан x .
2 Найдите sec (Arcsin x ). Не забудьте сделать набросок, чтобы помочь вам. Выберите значение, например x = −0,7, в качестве тестового примера для Проверьте свой ответ.Решение : Если угол A равен Arcsin x , то мы можем сделайте x противоположную сторону и 1 гипотенузу. Посредством теорема Пифагора, которая делает смежную сторону √1 — х . sec A поэтому сек (Arcsin x ) = 1 / √1 — x .
В ответе нет нечетных степеней x , поэтому мы не нужно беспокоиться о знаке x .
Давайте проверим это с помощью х = -0. 7:
Arcsin −0,7 ≈ −44,43, а
с -44,3 =
1 / cos −44,3 ≈ 1,40.
1 / √ (1 — 0,7) ≈ 1,40 также,
так что формула верна, по крайней мере, для этого теста.
7:
Arcsin −0,7 ≈ −44,43, а
с -44,3 =
1 / cos −44,3 ≈ 1,40.
1 / √ (1 — 0,7) ≈ 1,40 также,
так что формула верна, по крайней мере, для этого теста.
Решение : Если угол A равен Arccos 1/ x , мы можем установить гипотенузу на x , а прилегающую сторону на 1, поэтому что cos A = 1/ x по мере необходимости.Третья сторона составляет √ x — 1.
Что грешит А ? Это должно быть
√ x — 1/ x .
Но это выражение имеет нечетную степень x , поэтому нам нужно
проверьте знаки. Если x отрицательно, то Arccos x будет во втором квартале. Функция синуса имеет все положительные значения в
Q II, значит, у нас должен быть положительный ответ. Но как написано,
дробь отрицательна, если x отрицательна, поэтому требуется
знак абсолютного значения, как в примере 3. Наш окончательный ответ —
Наш окончательный ответ —
sin (Arccos 1/ x ) = √ ( x — 1) / | x |
Давайте проверим это с помощью х = -1,3: Arccos (1 / −1,3) ≈ 140,28, дюйм Q II, как ожидалось, и sin 140,28 ≈ 0,64, положительное число вроде синусы всех углов в Q II. √ ((- 1,3) — 1) / | −1,3 | ≈ 0,64 тоже. Итак, формула верна, по крайней мере, для этого теста даже с отрицательным x, положив угол в Q II, формула при необходимости возвращает положительное число.
Решения для части 10: развлечения с комплексными числами
1 Экспресс в форме a + b i: (а) 62∠240 (б) 100e 1.17iРешения : (а) 62 (cos (240) + i sin (240)) ≈ −31−53,69i
(b) очевидно в радианах, так как градусы отсутствуют. отметка. 100 (cos (1,17) + i sin (1,17)) ≈ 39.02 + 92.08i
2 Выразите в полярной форме в градусах и радианах: (а) −42 + 17i (б) 100i (в) −14,7 Решения :
(а) r =
√ (-42) + 17 ≈ 45,31. θ =
2 Арктан (17 / (- 42 + 45,31)) ≈ 2,76;
умножьте на 180 / π, чтобы получить 157,96.
Ответы: 45,31 цис 157.96 или
45,31 цис 2,76. Конечно, вы могли бы использовать
любые другие формы, показанные в главе.
θ =
2 Арктан (17 / (- 42 + 45,31)) ≈ 2,76;
умножьте на 180 / π, чтобы получить 157,96.
Ответы: 45,31 цис 157.96 или
45,31 цис 2,76. Конечно, вы могли бы использовать
любые другие формы, показанные в главе.
(b) и (c) — это пустяки, так как у вас нет
для вычисления радиуса или угла.
(б) 100i = 100∠90 или
100e iπ / 2
(в) −14,7 = 14,7∠180 или
14,7 e iπ
Решение : Сначала положите −i в полярную форму, что достаточно просто, поскольку −i на отрицательной оси y : −i = 1 цис 3π / 2.Затем примените формулу, уравнение 83:
(1 цис 3π / 2) 1/3 = 1 1/3 цис (π / 2 + 2π k /3) для k = 0, 1, 2
Три угла равны π / 2, π / 2 + 2π / 3 = 7π / 6 и π / 2 + 4π / 3 = 11π / 6 = 3π / 2.
(1 цис 3π / 2) 1/3 =
1 цис π / 2,
1 цис 7π / 6,
1 цис 11π / 6.
Вы знаете точные синусы и косинусы для любого числа, кратного π / 6, так что вам не нужен ваш калькулятор, чтобы конвертировать обратно в a + b i форма:
Кубические корни из −i: я, — (√3 / 2) — (1/2) я, (√3 / 2) — (1/2) я.
Между прочим, я не только кубический корень из −i, но −i — кубический корень из я. Я позволю тебе найти два других кубических корня я себя.
4 Найдите (1.04−0.10i) 16 .Решение : Сначала представьте это число в полярной форме: r = √1,04 + 0,10 ≈ 1.044796631. Затем найти θ = 2 Арктан (-0,10 / (1,04 + 1,044796631)) ≈ −0,09585
. (Мой калькулятор работает в радианах, но это не имеет значения, потому что я конвертирую обратно в в любом случае прямоугольный формат.) Так
(1.04−0.10i) ≈ 1,04796631 цис -0,09585
И поэтому
(1.04−0.10i) 16 ≈ 1,04796631 16 цис (-16; 0,09585
)
≈ 2,016082111 цис (-1,533746354)
≈ 0,0746787−2,01469853i
Что нового
- 6 ноября 2020 г.
 : страница преобразована из HTML 4.01 в HTML5, и
улучшено форматирование радикалов.
: страница преобразована из HTML 4.01 в HTML5, и
улучшено форматирование радикалов. - 20 декабря 2016 г. : в проблеме, которая создает вложенные радикалы, добавлена ссылка на технику на этом сайте за их разрушение.
- 11 декабря 2016 : Добавлены решения практических задач для Часть 5; добавлены три новых доказательства в части 7.
- 29 ноября 2016 г. : добавлены три новые задачи в части 3.
- 26/27 ноя 2016 : Добавлены решения для проблем Части 7 и Части 8.
- 19/20 ноября 2017 г. : Добавлены решения для части 1, части 3 и Часть 6 проблемы.
- 13 ноя 2016 : Добавлены решения для проблем Части 5. (Часть 5 был перенумерован в Часть 4 29 ноября 2016 г.)
- 30 октября 2016 г. : Добавлены решения для проблем Части 9 и Части 10.
- 27 октября 2016 г. : Новый документ (только задачи части 2).


 — 96 с.: ил. ISBN 5-7107-2667-2
— 96 с.: ил. ISBN 5-7107-2667-2 Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7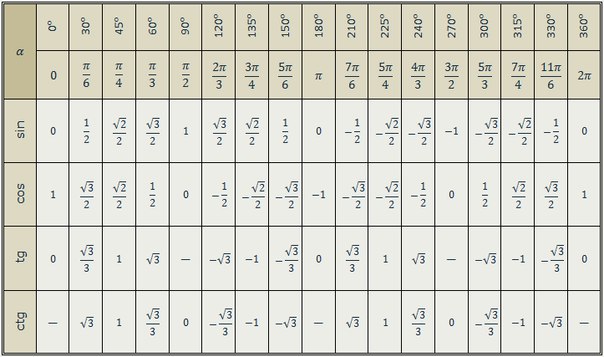 Так C должен быть <90 и B должен быть
> 90.
Так C должен быть <90 и B должен быть
> 90. : страница преобразована из HTML 4.01 в HTML5, и
улучшено форматирование радикалов.
: страница преобразована из HTML 4.01 в HTML5, и
улучшено форматирование радикалов.