Нет комментариев Разное

Арккосинус онлайн в градусах: Онлайн калькулятор: Обратные тригонометрические функции

Опубликовано

Арксинус и арккосинус. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти арксинус и арккосинус от числа. Результат можно видеть как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Функция арксинус и ее график

Как известно, функция синус определена в интервале [−∞;+∞] и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции синус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию синус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция sin x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arcsin y. Поменяв местами x и y, получим:

y=arcsin x.(1)

Функция (1) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой

y=x (Рис.2).

Свойства функции арксинус.

  1. Область определения функции: .
  2. Область значений функции: .
  3. Функция является нечетной: .
  4. Функция возрастает.
  5. Функция непрерывна.

Решим тригонометрическое уравнение

sin t=a.(2)

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором sin x>1 (см. график функции синус (Рис.1). При |a|≤1, в отрезке (дуга DAB) уравнение (2) имеет одно решение (см. Рис.3):

В отрезке (дуга DCB) функция синус убывает и принимает значения от 1 до −1. Следовательно в этом отрезке уравнение (2) также имеет решение:

Действительно:

А из

следует

т.е.

Таким образом уравнение (3) имеет два решения в отрезке :

которые совпадают при |a|=1.

Поскольку функция синус периодичная с основным периодом 2π, имеем

Тогда получим решение (2) в виде

Решения (3) и (4) удобно представить одним уравнением:

Действительно. При четных k (k=2n) из уравнения (5) получают все решения, представленные уравнением (3), а при нечетных k (k=2n+1) − все решения, представленные уравнением (4).

При a=1, arcsin a и π−arcsin a совпадают (т.к. ), следовательно решение уравнения sin t=1 имеет вид:

При |a|=−1, из (3) и (4) следует:

Но поворот эквивалентно повороту . То есть уравнения (6) и (7) эквивалентны. Тогда решение уравнения sin t=−1 запишем в виде:

При |a|=0, из (3) и (4) имеем следующее решение уравнения

sin t=0:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Функция арккосинус и ее график

Как известно, функция косинус определена в интервале [−∞;+∞] и не является монотонной функцией (Рис.4) (подробнее о функции косинус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию косинус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция cos x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arccos y

. Поменяв местами x и y, получим:

y=arccos x.(8)

Функция (8) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арксинус.

  1. Область определения функции: .
  2. Область значений функции: .
  3. Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
  4. Функция убывает.
  5. Функция непрерывна.

Решим тригонометрическое уравнение

cos t=a.(9)

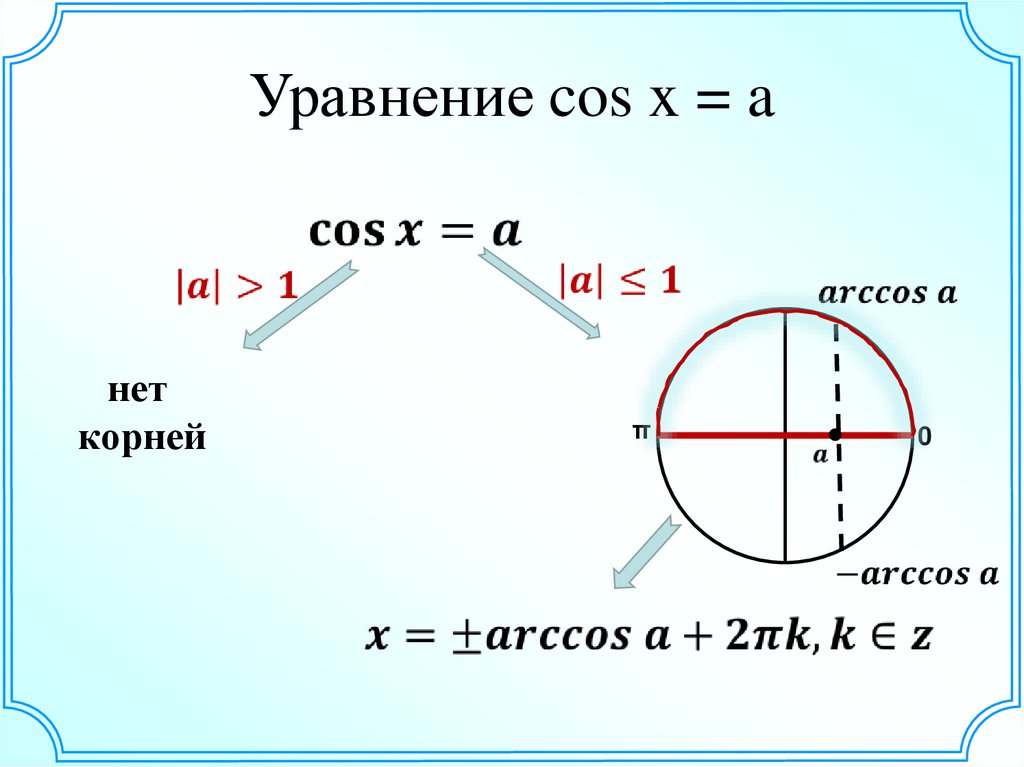
При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором cos x>1 (см.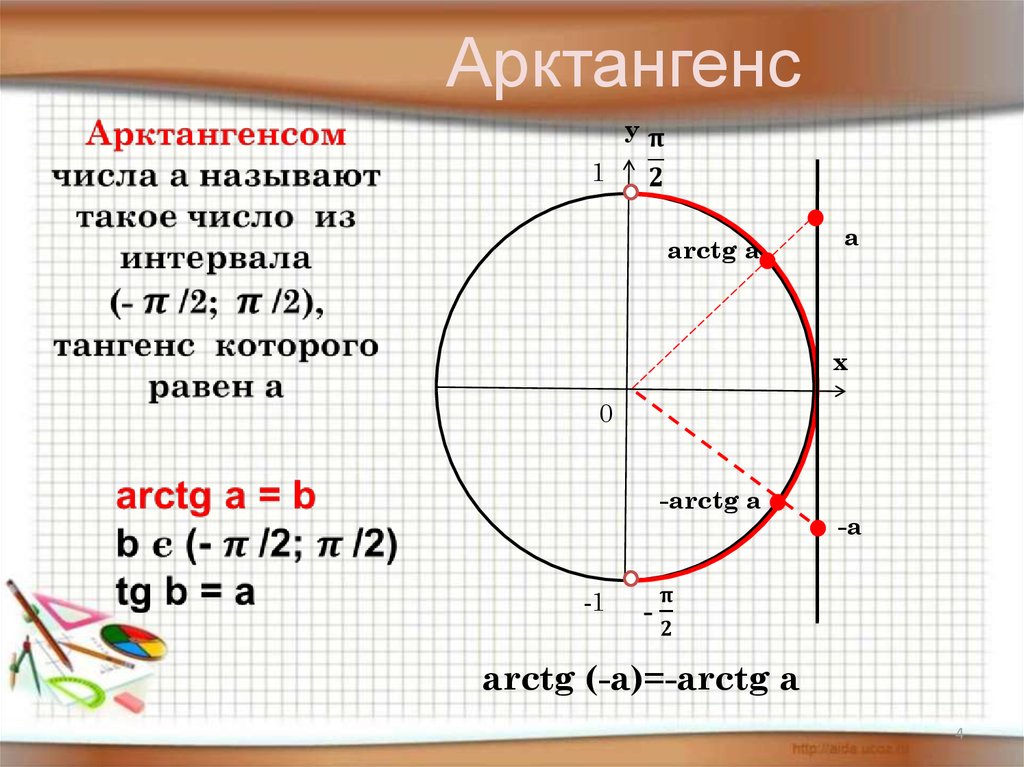

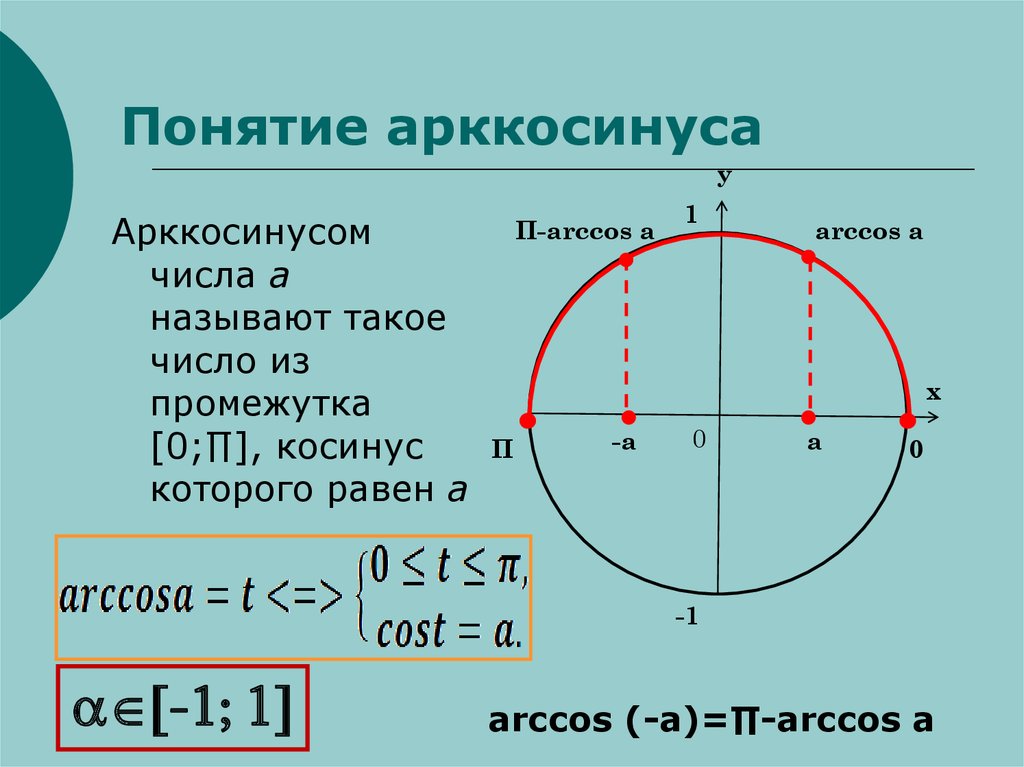
график функции косинус (Рис.4). При |a|≤1, в отрезке [0; π] (дуга ABC) уравнение (9) имеет одно решение t1=arccos a. В отрезке [−π; 0] (дуга CDA) уравнение (9) имеет одно решение t2=−arccos a(см. Рис.6):

Таким образом, в интервале [−π; π] уравнение (9) имеет два решения y=± arccos a, которые совпадают при a=1.

Поскольку функция косинус периодичная с основным периодом 2π:

то общее решение (9) имеет следующий вид:

При a=1, числа arccos a и −arccos a совпадают (они равны нулю), тогда решение уравнения cos t=1 можно записать так:

t=2πn, n∈Z.

При a=−1, имеем cos t=−1,

t=π+2πn, n∈Z

При a=0, имеем cos t=0,

Решение тригонометрического уравнения cos t=0 можно записать одним уравнением:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (10):

Так как , то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

Так как (), то

Пример 3. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

С помощью онлайн калькулятора вычисляем : . Тогда решение можно записать так:


определение, формула, таблица, график, свойства

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Обратная тригонометрическая функция: Арккосинус (arccos)

  • Определение
  • График арккосинуса
  • Свойства арккосинуса
  • Таблица арккосинусов

Определение

Арккосинус (arccos) – это обратная тригонометрическая функция.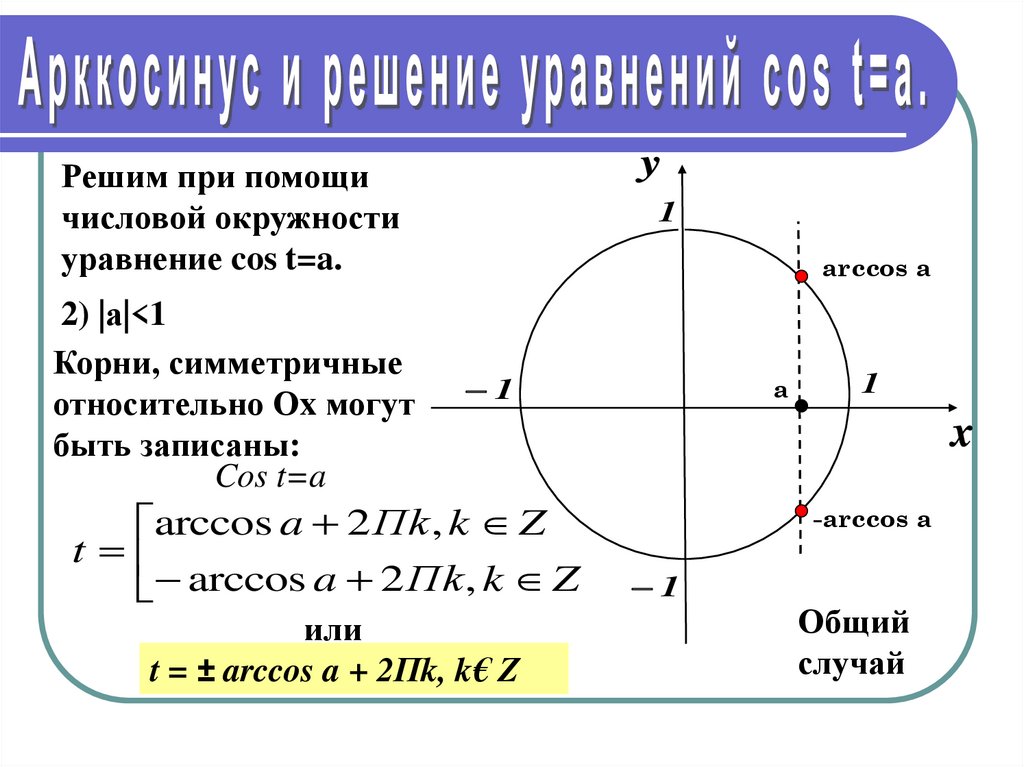

Арккосинус x определяется как функция, обратная к косинусу x, при -1≤x≤1.

Если косинус угла у равен х (cos y = x), значит арккосинус x равняется y:

arccos x = cos-1 x = y

Примечание: cos-1x означает обратный косинус, а не косинус в степени -1.

Например:

arccos 1 = cos-1 1 = 0° (0 рад)

График арккосинуса

Функция арккосинуса пишется как y = arccos (x). График в общем виде выглядит следующим образом:

Свойства арккосинуса

Ниже в табличном виде представлены основные свойства арккосинуса с формулами.

СвойствоФормула
Косинус
арккосинуса		cos( arccos x ) = x
Арккосинус
косинуса		arccos( cos x ) = x + 2kπ,
где k∈ℤ (k — целое число)
Арккосинус
отрицательного числа		arccos(-x) = π — arccos x = 180° — arccos x
Дополнительные углыarccos x = π/2 — arcsin x = 90° — arcsin x
Сумма
арккосинусов		 ru/wp-content/uploads/2020/02/arccos-summa-exc.png" class="stbSkipLazy aligncenter size-full" width="550" height="1166" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arccos-summa-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arccos-summa-exc.png" class="stbSkipLazy aligncenter size-full" width="550" height="1166" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arccos-summa-exc.png" />»>
Разность
арккосинусов		 ru/wp-content/uploads/2020/02/arccos-raznost-exc.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arccos-raznost-exc.png" class="stbSkipLazy aligncenter size-full" width="510" height="1052" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arccos-raznost-exc.png" />»>
Арккосинус
синуса		 5)π</span></nobr>»>arccos( sin x ) = —x — (2k+0.5)π
Синус
арккосинуса
Тангенс
арккосинуса		 ru/wp-content/uploads/2020/02/arccos-exc-2.png" class="stbSkipLazy aligncenter size-full" width="200" height="402" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arccos-exc-2.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arccos-exc-2.png" class="stbSkipLazy aligncenter size-full" width="200" height="402" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arccos-exc-2.png" />»>
Производная
арккосинуса		 ru/wp-content/uploads/2020/02/arccos-exc-3.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2020/02/arccos-exc-3.png" class="stbSkipLazy aligncenter size-full" width="270" height="560" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arccos-exc-3.png" />»>
Неопределенный
интеграл арккосинуса		 ru/wp-content/uploads/2020/02/arccos-exc-4.png" class="stbSkipLazy aligncenter size-full" width="310" height="630" data-full="https://microexcel.ru/wp-content/uploads/2020/02/arccos-exc-4.png" />»>

microexcel.ru

Таблица арккосинусов

xarccos x (рад)
arccos x (°)
-1π180°
-√3/2		5π/6150°
-√2/23π/4135°
-1/2		2π/3120°
0π/290°
1/2π/360°
√2/2π/445°
√3/2π/630°
100°

microexcel.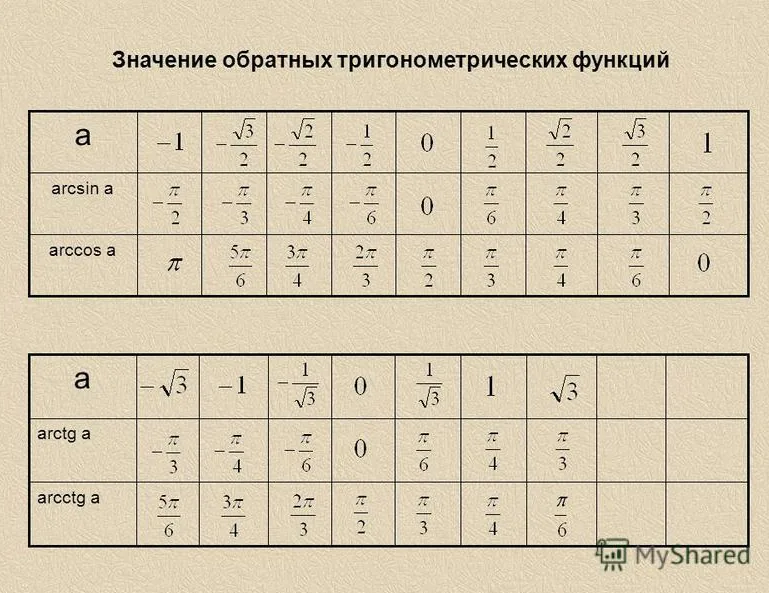 ru

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Калькулятор арккосинуса онлайн | Тригонометрия

Если у вас есть значение, полученное из косинуса, но вы хотите узнать исходный угол, вам следует применить функцию арккосинуса . Чтобы избежать каких-либо расчетов вручную, мы разработали онлайн-инструмент таким образом, что вам нужно ввести значение, которое у вас есть, которое должно быть между -1 и 1.

Затем нажмите кнопку расчета, чтобы получить угол и возможные эквиваленты для этого результата, вы также можете выбрать, хотите ли вы видеть его в градусах или радианах. Выбор ваш.

Разделы статей

  • Что такое аркокозен?
  • Производная арккосинуса
  • Интеграл аркокосинуса
  • Вычисление арккосинуса в Excel
  • Таблица функций Arccos
  • Аркокозен в Matlab

Что такое аркокозен?

Как объяснялось выше, арккосинус является обратной функцией косинуса . Применяя arccos, мы можем получить начальный угол, что мы, безусловно, будем часто использовать в задачах тригонометрии.

Формула arccos представлена ​​следующим образом:

arccos( x ) = cos -1 ( x )

Используя , мы хотим вычислить арккосинус 0, например, имеем:

arccos( 0 ) = cos -1 ( 0 ) = 90 градусов.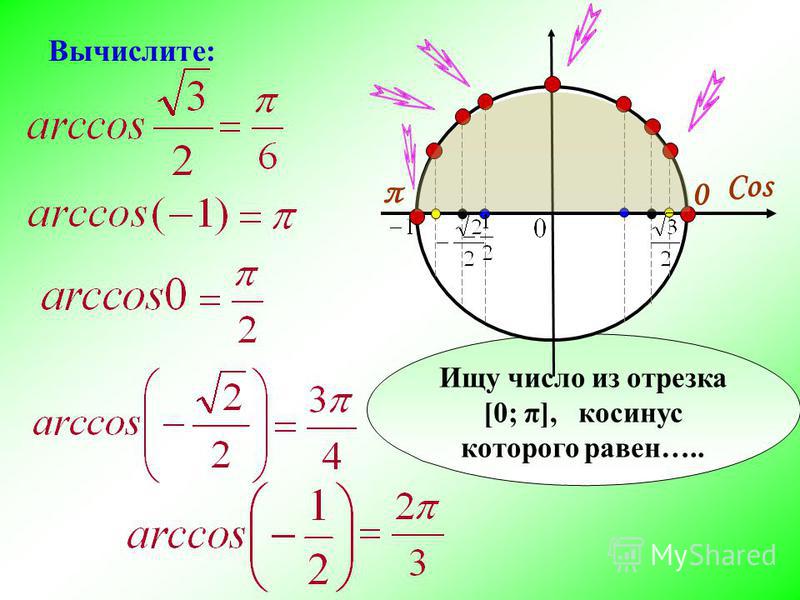

Производная арккосинуса

Производная арккосинуса функции равна производной функции, деленной на квадратный корень из единицы минус квадрат самой функции, все с знак минус перед .

Интеграл аркокозена

Чтобы составить интеграл функции арккосина , необходимо использовать интегрирование по частям следующим образом:

Чтобы окончательно получить следующий результат:

Если вы хотите, вы можете использовать Excel для вычисления арккосинуса значения в пределах диапазона функции, т. е. между -1 и 1.

При использовании Функция Excel ACOS вы автоматически получите угол, эквивалентный этому значению, через его арккосинус. Давайте посмотрим, как он используется в каждом случае для отображения результата в градусах или радианах.

Результат в радианах

По умолчанию, когда применяет арккосинус в Excel , мы получаем результат в радианах. Если это то, что вы ищете, просто введите следующую формулу в ячейку электронной таблицы:

=ACOS(A1)

Результат в градусах

Если вам нужно получить значение угла в градусах, Excel также позволяет вложить вторую функцию, чтобы при применении арккосинуса мы получали результат в градусах вместо в радианах. Для этого необходимо использовать следующую формулу:

=ГРАДУСЫ(ACOS(A1))

Помните, что A1 соответствует координатам ячейки, в которой находится значение y (между -1 и 1). Вы можете изменить эти координаты, чтобы адаптировать их к координатам вашей электронной таблицы.

Если у вас есть сомнения, рекомендуем посмотреть видео над этими строками, в котором мы демонстрируем, как использовать функцию ACOS в Excel для вычисления арккосинуса .

Таблица функций Arccos

Ниже мы собрали некоторые из них. другие.

y x=Arccos(y)  
Марки Радианы
-1 180° π
-0,8660254 150° 5π/6
-0,7071068 135° 3π/4
-0,5 120° 2π/3
0 90° π/2
0,5 60° π/3
0,7071068 45° π/4
0,8660254 30° π/6
1 0° 0

Аркокосин в Matlab

Если вам нужно вычислить арккосинус в Matlab для задания класса или любой другой задачи, вот как решить упражнение.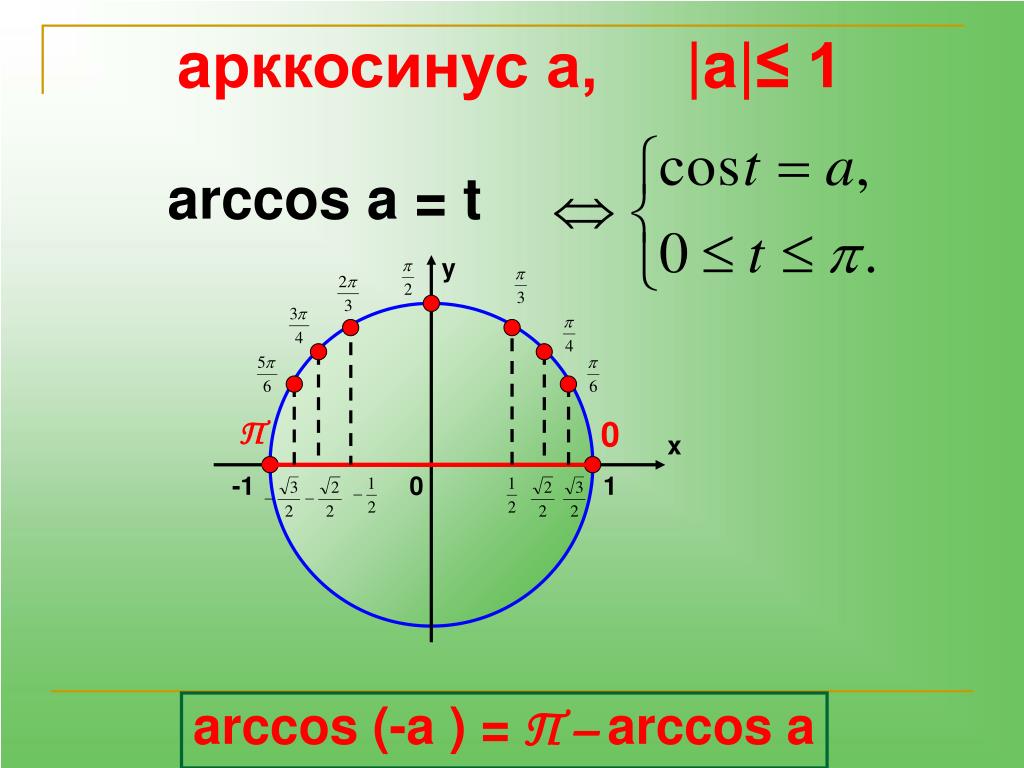

Если вы хотите рассчитать арккосинус и получить результат в радианах, это синтаксис функции Matlab:

acos(x)

Если вы хотите получить arccos в Matlab с результатом в градусах, то вы должны использовать это формула:

acosd(x)

Мы оставляем вам эту ссылку, по которой вы можете увидеть дополнительную информацию для Matlab и в которой они показывают вам с примерами, как рассчитать acos(x) или даже представить его на графике .

Начо

Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.

  • Аркотангенс
  • Калькулятор аркокозена
  • Калькулятор тригонометрии
  • Расчет аркосинуса онлайн
  • Косеканс 92)*2
    Он имеет множество функций, которые вы можете ввести (см. ниже)

    числа/изображения/decimal.js, числа/изображения/calc.js

    Примеры

    • Введите 12+2*3 (=18)
    • Выберите «градусы», введите cos(45) (=0,7071067811865476)
    • Введите 2/кв.(2) (=1,414213562373095)

    Ссылка на функцию

    Функция вернет NaN (не число), когда вы вводите недопустимые записи, такие как sqrt (−1)

    .

    Операторы

    9
      + Оператор сложения
      — Оператор вычитания
      * Оператор умножения
      / Оператор отделения
    Оператор степени/экспоненты/индекса
      () Скобки

    Функции

      кв Квадратный корень из значения или выражения.
      грех синус значения или выражения
      потому что косинус значения или выражения
      желтовато-коричневый тангенс значения или выражения
      как арксинус (арксинус) значения или выражения
      акос арккосинус (arccos) значения или выражения
      атан арктангенс (арктангенс) значения или выражения
      синх Гиперболический арксинус (арксинус) значения или выражения
      кош Гиперболический арккосинус (arccos) значения или выражения
      танх Гиперболический арктангенс (арктангенс) значения или выражения
      эксп e (константа Эйлера), возведенная в степень значения или выражения
      пер. Натуральный логарифм значения или выражения
      журнал Логарифм по основанию 10 значения или выражения
      абс Абсолютное значение (расстояние от нуля) значения или выражения
      град перевести радианы в градусы
      рад перевести градусы в радианы
      знак -1 для значений меньше 0, иначе 1
      круглый округлить до ближайшего целого числа
      этаж Возвращает наибольшее (ближайшее к положительной бесконечности) значение, которое не больше аргумента и равно математическому целому числу.
      потолок Возвращает наименьшее (ближайшее к отрицательной бесконечности) значение, которое не меньше аргумента и равно математическому целому числу.

    Leave a Reply

    Ваш адрес email не будет опубликован. Обязательные поля помечены *