Опубликовано Показываю 3 способа как быстро построить прямой угол на местности имея любую веревку | Строю для себя
Добрый день, уважаемые гости и подписчики канала «Строю для себя»!
Ниже описаны 3 приема восстановления перпендикуляра или построения прямого угла на местности к любой прямой линии. Данные мероприятия очень важны в строительстве при построении осей на плане и при сооружении обноски для дальнейшего возведения фундаментов или стен.
Имея только отрезок любой веревки, шнурки или троса, пользуясь данными способами — вы сможете совершенно точно построить перпендикуляр.
Итак, способ №1: Равнобедренный треугольник
Определяем точку на прямой линии, к которой будем строить перпендикуляр (для наглядности — я в эту точку воткнул шампур 🙂
Отмечаем по обе стороны от него две равноудаленные точки (с помощью веревки это очень просто сделать). Теперь мы имеем три точки, которые находятся на одной прямой линии и два равных отрезка между ними (на рисунке ниже — 3 шампура).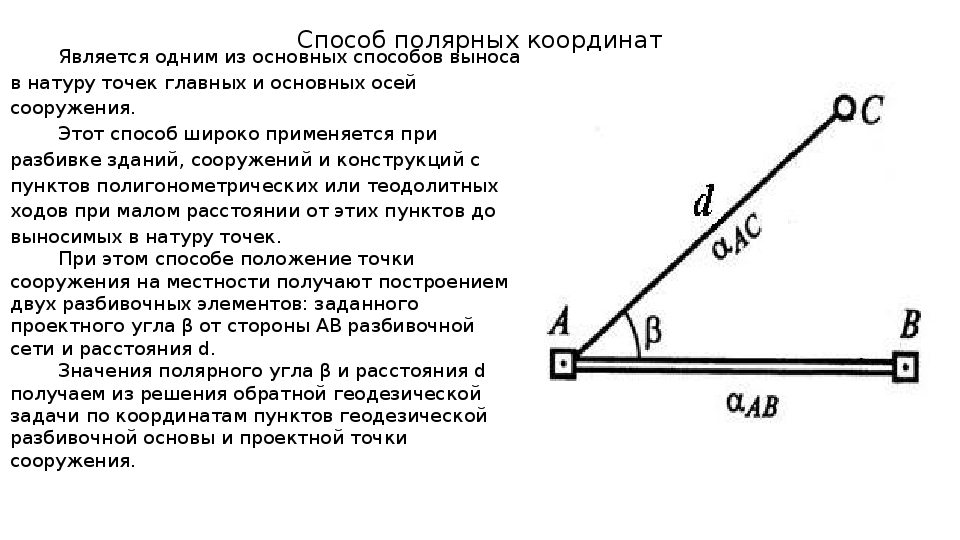
Затем, нам достаточно определить середину веревки произвольной длины (В своем случае, для удобства, я на противоположных концах сделал петли, накинул их на колышек (шампур) и натянул веревку, тем самым разделил ее на две равные части).
Теперь, концы веревки совмещаем с двумя крайними точками и натягиваем ее за найденную середину.
Перпендикуляр готов (Свойство равнобедренного треугольника, высота которого делит основание на два равных отрезка)
Способ №2: Пересечение двух дуг
Данный способ выручает, когда у вас есть только короткая веревка. Как и в предыдущем способе, нам требуется опять же построить три точки на одной прямой, где две крайние равноудалены от центральной.
Теперь, подобно циркулю, из каждой крайней точки рисуем дуги одинакового радиуса. Точка пересечения двух дуг и будет давать нам перпендикуляр к прямой.
Схематично, это выглядит так (точка О является точкой пересечения дуг):
Способ №3: Теорема Пифагора
Наверное, это самый используемый способ, в котором применяются равные отрезки в соотношении 3:4:5.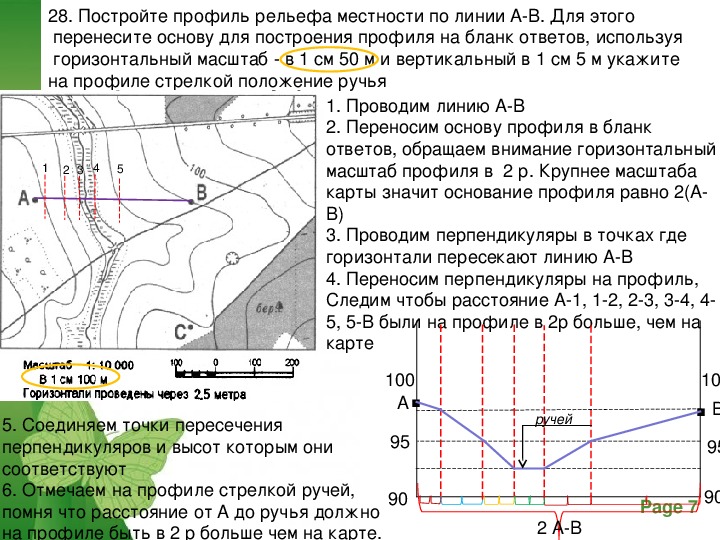
Данные отрезки могут измеряться в сантиметрах, метрах, километрах или любой произвольной длины, которую мы и будем использовать.
Для наглядности, я сделал на одной веревке 13 узлов с равными расстояниями друг от друга.
Теперь, достаточно просто туго растянуть веревку за вершины, которые отделяются между собой 3, 4 и 5 отрезками. Опять же, использую шампуры :-)))
Прямой угол построен!
На этом всё, спасибо за терпение :-)))
Если Вам было интересно, ставьте палец вверх и подписывайтесь на мой канал! Впереди много интересных тем!
Знания по геометрии на жизненных примерах и чего не хватает детям в школе?
Зная тригонометрию, можно не бегать по крыше с рулеткой
Какие деревья сажают, чтобы не откачивать яму?
Как определить высоту объекта на расстоянии?
Как рассчитать двутавр для перекрытия на прогиб и нагрузку?
Как измерить ширину реки с одного берега?
Как проверить прямой угол без угольника
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные
конструкции, требующие прямого угла в 90 градусов.
Обыкновенный угольник не может позволить проверить или
разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или
проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:
a²+b²=c²
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза.
Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную.
А следовательно можем
размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол.
На стенах (на одной высоте) или на полу отмечаем на обоих
стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно
больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250
см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат
(умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 —
это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра
должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали —
проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же,
не на всех мобильных устройствах калькуляторы умеют извлекать его.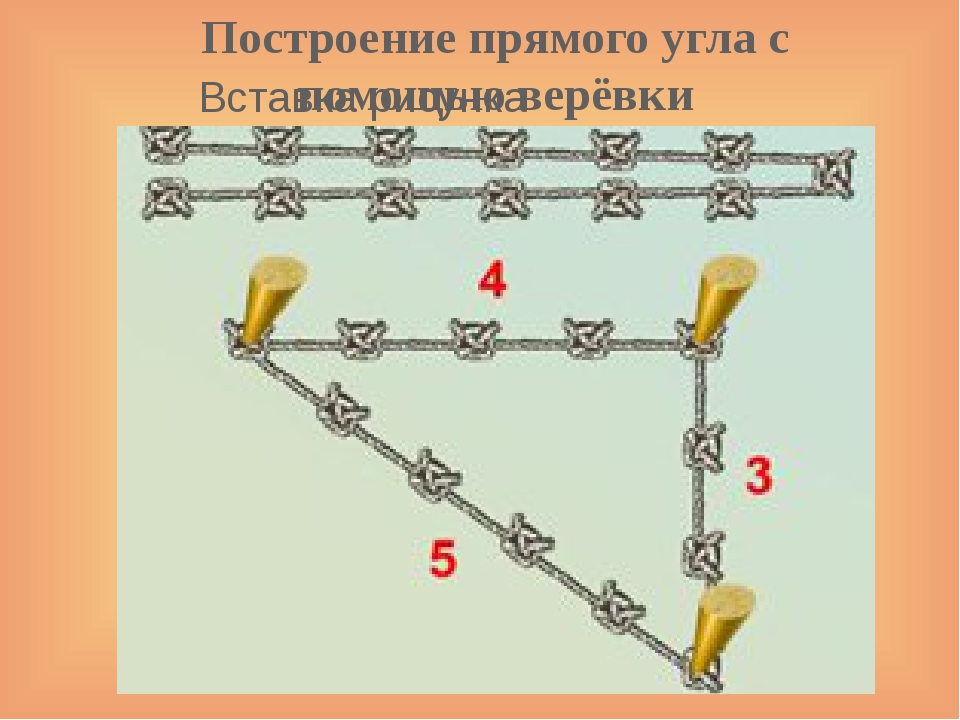
Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое
нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из
понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см.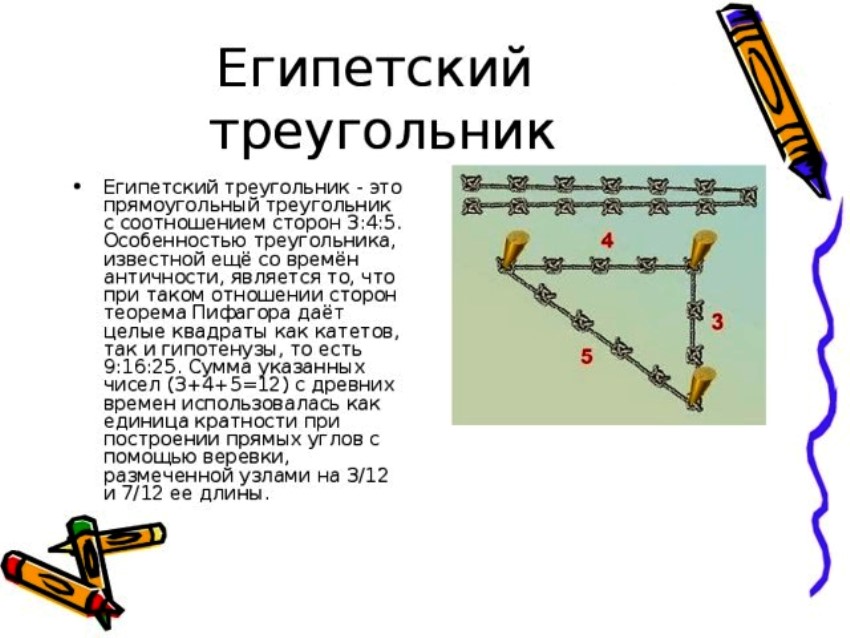
в несколько миллиметров
не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся
последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см.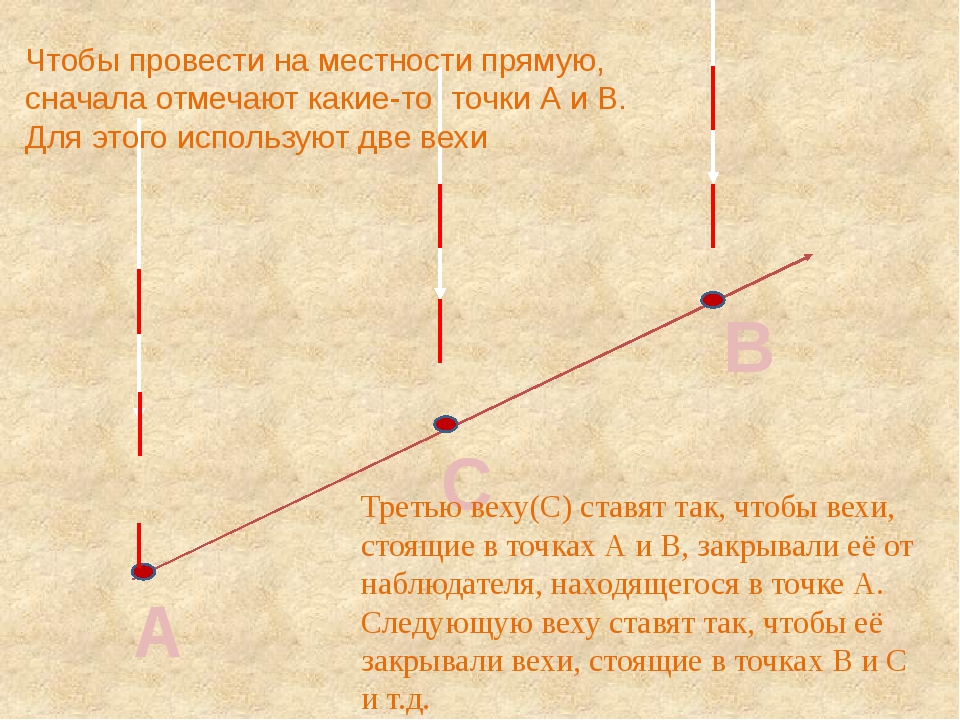
нужно умножать на
количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных
фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные
или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается
прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить
45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим
два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм
вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
Оцените публикацию: Оценка: 4.3 (113 голосов)Смотрите также другие статьи
Построение прямых углов на местности
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Построение прямых углов на местности
На практике часто приходится строить прямые углы на местности.
Простейший прибор, который служит для этого, — это экер. Экер состоит из двух брусков расположенных под прямым углом, и закрепленных на треножнике (Рис. 1). На краях брусков вбивают гвозди так, что прямые, которые проходят через них перпендикулярны друг другу. Отвес служит для точной установки экера в нужное место на местности.
Пример: Чтобы построить прямой угол с заданной стороной ОА, треножник с экером устанавливают в том месте, где должна располагаться вершина прямого угла (в нашем случае точка 
Затем необходимо установить один из брусков так, чтобы его направление совпадало с направлением заданной стороны (в нашем случае OA), совмещение этих направлений можно осуществить с помощью вехи, установленной в точке А. Далее по направлению второго бруска провешивают прямую линию (в нашем случае ОВ). Получаем прямой угол АОВ на местности (Рис.2).
Существуют и более совершенные приборы для построения прямых углов, так, например, в геодезии используют теодолит.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Длина отрезка
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Смежные углы
Вертикальные углы
Перпендикулярные прямые
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.
com, 2021
Пользовательское соглашение
Copyright
Как высчитать угол 90 градусов рулеткой
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов.
Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин.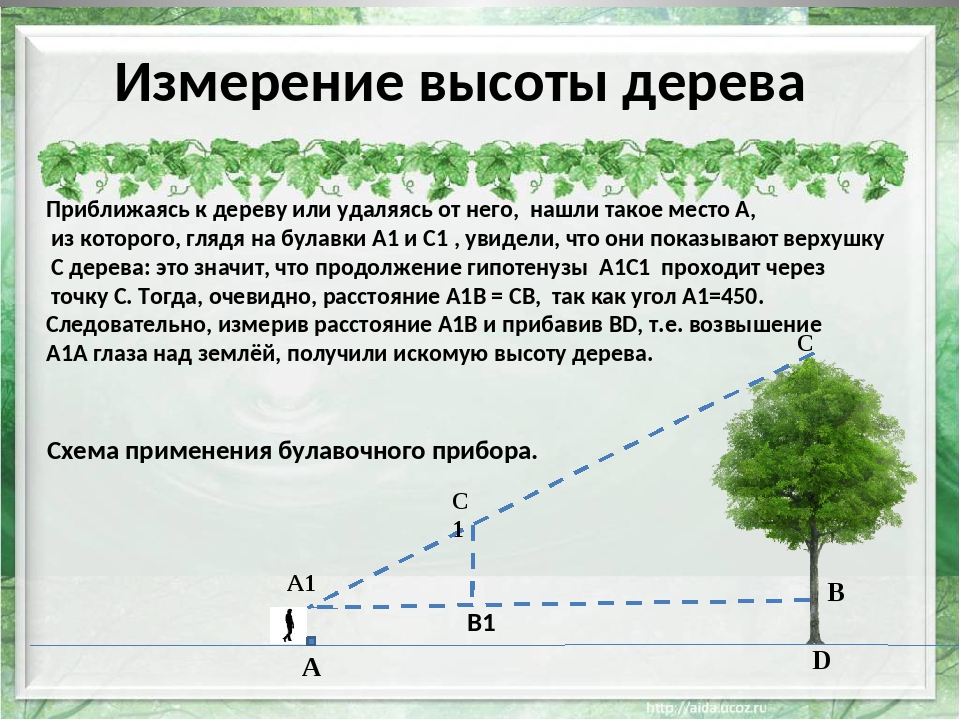
Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см.
Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое.
Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
При ремонте, строительстве или самостоятельном изготовлении мебели часто бывает необходимо проверить или построить прямой угол. В любом случае, очень важна точность измерения, но если стороны угла равны нескольким метрам, то это сложно будет сделать с помощью угольника.
Сегодня мы рассмотрим несколько универсальных методов замера прямого угла с помощью рулетки.
Проверить прямой угол поможет известная каждому со школьных времен теорема Пифагора. Вспомним определение: ”В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов” ( a 2 + b 2 = с 2 ), где a и b – катеты, а с – гипотенуза. Подставив в формулу известные нам две величины, получим неизвестную третью.
А теперь вернемся к нашим замерам и применим теорему на практике.
Для того, чтобы проверить угол, отмечаем на обеих стенах произвольные отрезки, желательно отмерять их побольше, чтобы удобнее было отмерять диагональ между ними. После того, как вы отметили эти отрезки, возведите длину каждого в квадрат и сложите. Из полученного результата извлеките квадратный корень (для удобства можно воспользоваться калькулятором). Теперь замеряем рулеткой длину диагонали между двумя отрезками, она должна совпадать с полученным результатом.
Если в результате измерения получилось другое число, то угол не равен 90 градусов.
Также не стоит забывать и о такой геометрической фигуре, как египетский треугольник – прямоугольник с длинами сторон 3, 4, 5, причем совершенно не важно в каких величинах, ведь между катетами длиной 3 и 4 угол, равный ровно 90 градусов. Давайте проверим?
a 2 + b 2 = (3 2 + 4 2 ) = (9 + 16) = 25; √25 = 5.
Как проверить угол с помощью египетского треугольника?
Отмерьте на одной стене отрезок длиной 3 метра, а на другой – отрезок длиной 4 метра. Теперь измеряем расстояние между двумя этими отметками точно так же, как в способе с теоремой Пифагора. Если получившийся результат кратен 5, то в том, что полученный угол равен 90 градусов, можно не сомневаться.
Как отмерить угол, используя рулеткуМожно самостоятельно смастерить угольник для замера углов:
- Соединяем две рейки одна перпендикулярно другой.
- Измеряем на одной рейке 60 см, на другой 80, лишнее обрезаем.
- Прибиваем третью рейку к одной отметке.
- Измеряем гипотенузу, прибиваем рейку ко второй метке.
- Еще раз проверяем размеры и при необходимости фиксируем ещё в нескольких местах.
- Обрезаем лишние концы.
Как видите, знание нескольких простых школьных теорем может помочь и в строительстве, и в ремонте. Зная несколько простых хитростей, вы всегда с легкостью можете создать или проверить прямой угол.
Строительная рулетка для электрика является таким же обязательным инструментом, как и индикатор напряжения. Даже у тех профессионалов, которые имеют в комплекте инструмента осепостроители и лазерные дальномеры, непременно в подсумке всегда присутствует обыкновенная рулетка.
Без нее не обойтись ни при разметке трасс электропроводки, ни при монтаже подрозетников.
Однако далеко не каждый знаком со всеми секретами и дополнительными возможностями при использовании строительной рулетки.
У нее оказывается очень много скрытых способностей, которые помогут вам заменить сразу несколько инструментов и значительно сэкономить время на ремонт.
Кстати, один из важных советов, для тех кто пользуется китайскими дешевыми рулетками заключается в следующем — если у вас именно такой экземпляр, то старайтесь все замеры делать одной рулеткой.
Один и тот же размер при измерении разными рулетками может не совпадать.
Один знакомый измерял расстояние стен в доме китайским инструментом, а в магазине при покупке материалов воспользовался их рулеткой. В итоге, дома очень был удивлен результатом покупки.
Подвижный зацеп сегодня встречается почти на каждой рулетке. И эта штука вовсе не для того, чтобы удобно спину почесать 🙂
Новички вообще нередко думают, что это какой-то брак. Какая в итоге будет точность, если один из ключевых элементов болтается и не закреплен надежно? Некоторые даже умудряются его заклепать сразу же после покупки.
Оказывается, что подвижный зацеп это необходимость, без которой вообще не возможна нормальная работа.
Объясняется это тем, что измерения рулеткой можно производить двумя способами:
- от предмета
Когда вы измеряете расстояние от предмета, зацеп выполняет роль нулевой точки. При измерении с захватом предмета, зацеп выдвигается на свою толщину. Тем самым нулевая отметка снова совпадает с краем предмета.
Поэтому не стоит сматывать строительную рулетку с эффектным щелчком в конце, тем самым вы только сократите срок ее службы.
Еще во многих моделях лента рулетки в самом начале на расстоянии 2,5см имеет отверстие. Сделано оно не просто так, а опять же чтобы облегчить вашу работу в одиночку.
Когда не за что закрепиться зацепом или неудобно им пользоваться из-за косой поверхности, простым шилом или гвоздиком через отверстие намертво закрепляете ленту и растягиваете ее на любую длину.
Воспользовавшись таким отверстием в рулетке вам не придется применять подобные захваты как на фото ниже. А всю работу по разметке можно легко проделывать без напарника.
Как вы понимаете при замерах в углах, серединой ленты рулетки очень трудно залезть непосредственно в угол. Также неудобно делать точные измерения в дверном или оконном проеме.
Поэтому в том случае когда нужно замерить проем, используйте корпус как продолжение рулетки.
На внешней стороне самой рулетки указан размер корпуса, который и нужно прибавить к показаниям ленты при измерении.
Если такого размера на корпус не нанесено, никто вам не мешает самостоятельно его измерить и написать в любом удобном месте.
Есть еще способ сделать подобные замеры с применением малярной ленты. Наклеиваете на поверхность кусочек ленты и производите два измерения в противоположных направлениях.
При этом карандашом в качестве метки лучше ставить галочки, а не простые черточки. Они будут визуально точнее показывать отметку. Тогда как черточка может быть нарисована криво, что и вызовет погрешность.
Проделав два измерения нужно сложить результаты и получите точный размер.
На многих зацепах рулетка имеет небольшое отверстие. Этим отверстием удобно зацепиться за шуруп или гвоздь. После этого зацеп уже никуда не соскочит.
Особенно это полезно, когда вы в одиночку проводите измерения на больших расстояниях. Погрешность измерения при этом будет не более 1-2мм, так как центр шурупа находится практически на нулевой отметке ленты.
Еще при помощи этого разъема в зацепе очень удобно рисовать окружности. Не нужно при себе иметь ни циркуля, ни транспортира.
В некоторых моделях зацепы выполняют магнитными. Помимо прямого их назначения, такими зацепами удобно поднимать упавшие предметы не слезая со стремянки.
Если применить небольшую доработку к дешевой рулетке, то из одного инструмента получается отличное приспособление для разметки.
Берете ножку циркуля, которая применяется с простыми карандашами, и закрепляете ее на внешней стороне рулетки.
Эту конструкцию можно сделать съемной, или вообще приспособить под отдельную рулетку.
Таким устройством очень удобно делать различные отметки или пользоваться им как рейсмусом.
А при использовании шурупа легко рисуются окружности нужного диаметра.
Если вы работаете с гипсокартоном или другой поверхностью, которую можно безопасно поцарапать, то рулетку стоит переделать под еще одну возможность. Надфилем на зацепе делаете зазубрины.
После чего с помощью этого зацепа легко делаются отметки на поверхности. При этом уже даже не обязательно чтобы под рукой был карандаш.
Внешнюю часть рулетки легко превратить в мини напоминалку или поверхность для записей. Берете малярную ленту и наклеиваете сбоку рулетки.
Если нет под рукой малярки, то можно писать прямо на самом корпусе.
Правда для этого, сначала надо пройтись по поверхности наждачкой нулевкой.
Так вы сделаете ее несколько бархатной, после чего надписи будут наноситься горазд легче.
Писать конечно нужно карандашом, после чего все это легко стирается резинкой.
С помощью строительной рулетки очень легко разделить любое число с точность до миллиметра пополам, не прибегая к услугам калькулятора.
Берете размер на рулетке, к примеру 116см — и сложив ленту пополам совмещаете с ним нулевую отметку, там где верхний зацеп.
Ровно в месте перегиба и будет требуемый результат — 58см.
Этим же способом можно не только делить, но и отнимать. Например общая длина стенки у вас 2м 11см, а распредкоробка находится от первого края на расстоянии в 1м 38см. Вам нужно быстро узнать сколько остается от этой распредкоробки до другого края стены, чтобы отмерить кабель канал.
Вытягиваете ленту на 2м 11см и складываете ее пополам.
Затем ищете отметку в 1м 38см. Как раз напротив нее, на второй половине ленты, и будет показано нужное вам расстояние — 73см.
Используя обыкновенную ленту рулетки можно легко разделить рабочую поверхность или заготовку на требуемое количество равных частей. Данный метод подходит в первую очередь для больших поверхностей — для труб или кабель каналов уже не сработает.
Как вы поступаете обычно? Замеряете общую длину или ширину, затем делаете вычисления и делите расстояние на нужное количество частей. После чего вновь линейкой или рулеткой отмеряете на поверхности эти части.
Оказывается все это можно проделать без калькулятора и даже без вычислений. Берете на рулетке число, которое больше чем ширина заготовки, и при этом кратно той величине, на которое вы хотите разделить расстояние.
Например ширина доски 17см, а вам ее нужно разделить на четыре равные части. Сдвигаете рулетку по диагонали до ближайшей отметки в 20см. После чего легко делите эти 20см на 4 и отмечаете метки на расстояниях 5см, 10см, 15см, 20см.
В итоге вы всего одним движением рулетки разделили поверхность на нужное количество частей.
Захотели поделить на 6 частей — ничего сложного. Можно сдвинуть диагональ до 30см и проделать то же самое.
Еще рулеткой на круглой трубе можно точно отмерить поперечный срез. Для этого плотно прижимаете по периметру трубы ленту, совместив концы. Если совместили ровно, никак иначе как под углом в 90 градусов она не ляжет.
Чем шире лента рулетки, тем предпочтительней. Проделать такой же фокус можно и с простым листком бумаги.
Когда невозможно измерить диаметр трубы или заготовки с торца, опять поможет строительная рулетка и геометрия. Обхватываете трубу лентой и измеряете ее окружность. После чего полученный результат нужно разделить на число Пи = 3,14. Это и будет необходимый диаметр.
Еще раз применив знания геометрии, строительной рулеткой без угольников и других инструментов можно проверить точность прямого угла. Как вы знаете из школьного курса — сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
Берете любую поверхность где должен быть прямой угол, например две стены комнаты. Отмеряете рулеткой в одну сторону 30см, а в другую 40см и ставите метки. Если угол действительно прямой и строители не накосячили, то соединив эти две метки по гипотенузе, вы должны получить на рулетке расстояние ровно в 50см.
Такой метод применим к любым поверхностям и изделиям. Главное что вам нужно соблюдать при измерении — это пропорции 3 -4 -5.
Если вы еще не приобрели себе рулетку, подобрать необходимую модель и ознакомиться с текущими ценами на них можно здесь.
Полезная геометрия | Наука и жизнь
В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.Вешаем зеркало
Вы решили повесить в прихожей зеркало. Тут же возникает вопрос: какой минимальной высоты должно быть зеркало, чтобы человек среднего роста мог видеть себя в нём целиком? И ещё: имеет ли при этом значение размер помещения, где будет висеть зеркало? Решение. Предмет и его отражение симметричны относительно плоскости зеркала. Построим в нём изображение человека (рис. 1): АВ — человек, А1В1 — его изображение, точка С — глаз, DE — зеркало. Из рисунка видно, что минимальная высота зеркала приблизительно равна половине роста человека, считая от уровня глаз. При этом высота Е нижнего края зеркала от пола должна быть вдвое меньше расстояния от пола до глаз. Легко понять, что, на каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нём с головы до ног, значит, размер помещения значения не имеет.Завариваем чай
Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше? Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d2).Выдерживаем прямые углы
Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»? Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строи-тельный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.Строим прямой угол на земле
Известен старинный способ постро-ения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ? Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 5. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.Проверяем перпендикулярность стен
Как проверить, перпендикулярны ли друг другу соседние стены в комнате, воспользовавшись верёвкой с узелками из предыдущей задачи? Решение. Если предположить, что стены в комнате вертикальны, а пол горизонтален, то проверку проводят так. От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы (рис. 6). Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный тре-угольник со сторонами 3, 4, 5 — прямоугольный.Отмеряем нужный объём
Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам? Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна (рис. 7). Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно (рис. 8). А можно ли геометрическим способом узнать объём бутылки? Конечно! Для этого надо заполнить бутылку водой чуть меньше чем наполовину (рис. 9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объём бутылки равен сумме найденных объёмов. Для точности можно учесть толщину стенок бутылки.Укрепляем калитку
Прямоугольная калитка (рис. 10, слева) со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать. Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.Выбираем табурет
Если вы решили предыдущую задачу, то без труда определите, на какой табурет (рис. 11) можно сесть без риска оказаться на полу. Решение. Безопасный табурет изображён на правой картинке, так как его сиденье и ножки образуют треугольник.Исправляем ошибку кроя
Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку? Решение. Для исправления ошибки вы можете разрезать один из треугольников, например так, как показано на рис. 12, а затем сложить из него нужный треугольник.Находим середину
Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня? Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести (рис. 13).Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
Разметка под фундамент своими руками
В данной статье опишем процесс разметки участка под фундамент своими руками.
План статьи:
Общие правила для разметки фундамента
Построение прямоугольного фундамента (т.Пифагора)
Построение прямоугольного фундамента (метод паутина)
Разметка под столбчатый фундамент
Разметка под ленточный фундамент
Разметка под плитный фундамент
Общие правила для любого фундамента
Выбираем точку отсчета. Первую сторону нашего фундамента нужно привязать к какому-нибудь объекту нашего участка.
Пример. Сделаем так, чтобы наш фундамент (дом) был параллелен одной из сторон забора. Следовательно, первую бечевку натягиваем равноудалено от этой стороны забора на нужное нам расстояние.
Построение прямого угла (90⁰). В качестве примера будем рассматривать прямоугольный фундамент, в котором все углы максимально близки к 90⁰.
Существует несколько способов как это сделать. Мы рассмотрим 2 основных. © www.gvozdem.ru
Способ 1. Правило золотого треугольника
Для построения прямого угла будем применять теорему Пифагора.
Формула
Чтобы не углубляться в геометрию попробуем описать проще. Чтобы между двумя отрезками a и b сделать угол в 90⁰ нужно сложить длины этих отрезков и вывести корень из этой суммы. Получившиеся число будет являться длинной нашей диагонали соединяющей наши отрезки. Очень просто расчет сделать с помощью калькулятора.
Обычно при разметке фундамента берут размеры сторон, чтобы при выведении из корня получалось целое число. Пример: 3х4х5; 6х8х10.
Если у вас есть рулетка, то в целом проблем не возникнет, если вы будете брать отрезки отличные от общеиспользуемых. Например: 3х3х4,24; 2х2х2,83; 4х6х7,21
Если измерения мы производили в метрах, то значения получаются очень даже понятными: 4м24см; 2м83см; 7м21см.
Калькулятор
Также стоит отметить, что измерения можно производить в любых системах измерения длины главное использовать известное нам соотношение сторон: 3х4х5 метра, 3х4х5 сантиметра и т.п. То есть, если даже у вас нет инструмента для измерения длины, то можно взять, например, рейку (длина рейки не имеет значения) и померить ей (3 рейки х 4 рейки х 5 реек).
Теперь давайте посмотрим как это применить на практике.
Инструкция по разметке прямоугольного фундамента
Способ 1. Правила золотого треугольника (т.Пифагора)
Рассмотрим на примере построение прямоугольного фундамента с размерами 6х8м с помощью золотого треугольника (т.Пифагора).
1. Размечаем первую сторону фундамента. Это самая простая часть в построении нашего прямоугольника. Главное, что нужно помнить. Если хотим чтобы наш фундамент (дом) был параллелен одной из сторон забора либо другого объекта на участке или за его пределами, то первую линию нашего фундамента делаем равноудаленной от выбранного нами объекта. Данную процедуру мы описывали выше. Для размещения первой бечевки можно использовать колушки, прочно закрепленные в грунте, но в идеальном варианте для данной цели использовать обноску. Ее и будем использовать. Расстояние между обносками для данной стороны сделаем 14м: между обносками и будущими углами по 3м и 8м под фундамент.
2. Натягиваем вторую бечевку максимально перпендикулярно первой. Идеально перпендикулярно на практике натянуть сложно, поэтому на рисунке мы также отобразили ее не много отклоненной.
3. Скрепляем обе бечевки в точке пересечения. Скрепить можно скобкой либо скотчем. Главное чтобы надежно.
4. Приступаем к формированию прямого угла с применением теоремы Пифагора. Будем строить прямоугольный треугольник с катетами 3 на 4 метра и гипотенузой 5 метров. Для начала отмеряем на первой бечевке 4 метра от места пересечения бечевок, а на второй 3 метра. Ставим отметки на шнурке с помощью скотча (прищепка и т.п.).
5. Соединяем рулеткой обе отметки. Один конец рулетки фиксируем у отметки в 4 метра и ведем в сторону отметки в 3 метра на другой бечевке.
6. Если у нас прямоугольный треугольник, то обе отметки должны сойтись при расстоянии в 5 метров. В нашем случае отметки не сошлись. Поэтому перемещаем бечевку в нашем случае вправо до того момента когда отметка на 3 м совпадет с делением рулетки на 5 м.
7. В итоге у нас получился прямоугольный треугольник с углом в 90⁰ между двумя бечевками.
8. Больше отметки нам не нужны и их можно убрать.
9. Приступаем к построению прямоугольника. Отмеряем на обеих бечевках длины сторон нашего фундамента 6 и 8 метров соответственно. Ставим отметки на бечевках.
10. Натягиваем третью бечевку максимально перпендикулярно к первой бечевке. Скрепляем обе бечевки на отметке в 8 м.
11. Натягиваем четвертую бечевку максимально перпендикулярно ко второй бечевке. Скрепляем обе бечевки на отметки в 6 метров.
12. Делаем отметки на третьей бечевке 6 метров и на четвертой 8 метров.
13. Чтобы получить четырехугольник с прямыми углами в нашем случае необходимо, чтобы обе отметки на третьей и четвертой бечевках совпали. Для этого перемещаем обе бечевки до момента соединения отметок.
14. В итоге, если все правильно измерили, то у нас должен получиться правильный прямоугольник. Давайте проверим, получился ли он с помощью измерения диагоналей.
15. Измеряем длины диагоналей. Если они одинаковые, как в нашем случае, мы имеем правильный прямоугольник. Диагонали имеют одинаковую длину и в равнобедренной трапеции. Но у нас известен один угол в 90⁰, а в равнобедренной трапеции таких углов нет.
16. Готовая разметка прямоугольного фундамента с применением теоремы Пифагора. © www.gvozdem.ru
Способ 2. Паутина
Очень простой способ сделать разметку в виде прямоугольника с углами в 90⁰. Самое главное что нам понадобится — это бечевка, которая не растягивается, и точность ваших измерений с помощью рулетки.
1. Нарезаем куски бечевки, которые нам понадобятся для формирования разметки. В данном примере мы строим фундамент со сторонами 6 на 8 метров. Также для правильного построения прямоугольника нам понадобятся равные диагонали, которые для прямоугольника 6 на 8 метров будут равны 10 метрам (т.Пифагора описана выше). Также нужно взять запас длины бечевок на крепление.
2. Соединяем нашу «паутину» как на рисунке. Скрепляем стороны с диагоналями в 4 местах по углам. Сами диагонали в точке пересечения скреплять не нужно.
3. Натягиваем первую бечевку (точки 1,2). Крепить ее будем с помощью колышков. Главное чтобы колышки крепко держались в земле и при натяжении нашей конструкции их не увело. Этот важный момент нужно учесть.
4. Натягиваем угол 3. Главное условие чтобы бечевка 1-3 и диагональ 2-3 не провисали и были максимально натянуты. После фиксации с помощь колышка в точке 3 мы имеем угол в точке 1 в 90⁰.
5. Натягиваем угол 4 и устанавливаем колышек. Следим, чтобы бечевка в точках 2-4, 3-4 и диагональ 1-4 не провисали и были максимально натянуты.
6. Если соблюдены все условия, то в результате у нас должен получиться прямоугольник с углами максимально близкими 90⁰.
Разметка под фундамент дома
Разметка под столбчатый фундамент
Делаем двухъярусную обноску. Нижний ярус – это уровень столбов.
Верхний ярус обноски – уровень ростверка.
Подробную инструкцию читаем в статье: Разметка под столбчатый фундамент с ростверком
Разметка под ленточный фундамент
Создаем прямоугольник для внешнего контура применяя т.Пифагора. Затем отступаем на величину, равную ширине ленты и делаем внутренний контур.
Разметка под плитный фундамент
Самой простой способ разметки. Строим прямоугольник по размерам фундамента применяя теорему Пифагора для нахождения прямого угла. © www.gvozdem.ru
От автора
В данной статье мы рассмотрели, как произвести разметку под фундамент своими руками с построением прямоугольника с углами в 90⁰. В целом ничего сложно в разметке нет. Цена вопроса – это стоимость бечевки, доски для обноски (эконом вариант — колышки) и умение пользоваться рулеткой.
Похожие статьи:
Как на местности построить прямой угол. Как быстро и точно разметить большой участок земли под фундамент сельского дачного дома.
Привязка зданий и сооружений к местности, разметка дома
Начиная изучение геометрии, на первом же уроке рассказывают, что геометрия с греческого переводится как измерение земли. А когда однажды приходится что-то строить или ремонтировать, и появляется необходимость мерить землю в прямом смысле этого слова, оказывается, что этого-то в школе и не преподавали! Потому что рисовать план дома на бумаге – это одно, а объяснять экскаваторщику, где и сколько копать, стоя на поросшем травой пустыре – совсем другое.Содержание1. Построение прямого угла на местности.2. Определение высоты и глубины на местности, высотные отметки.
Но не святые горшки лепят, после изучения информации далее, вы сумеете и выполнить разбивку котлована будущего здания, и осуществить привязку к местности сооружения, существующего только на бумаге, определить высоты, построить горизонтальную линию, при этом используя самые простые инструменты.
Построение прямого угла на местности
Начнем с самого важного – построения прямого угла на местности. Сделать это несложно, а из инструментария нужна только десятиметровая рулетка, четыре колышка и моток капронового шнура.
Определяем линию, от которой будем строить прямой угол. К примеру, это стена будущего здания. Забиваем два колышка и натягиваем между ними шнур. Расстояние между колышками берем произвольное, но несколько больше четырех метров.
Колышек А будет вершиной нашего угла, а натянутый шнур – одной из сторон. Отмеряем от колышка А вдоль шнура четыре метра и забиваем колышек С.
Теперь нам понадобятся помощники. Один из них держит начало, или ноль, рулетки на колышке А, второй – на колышке С держит отметку 8 метров. Вы берете ленту рулетки на отметке 3 м и натягиваете ее так, чтобы образовался треугольник, одним из катетов которого будет натянутый шнур, вторым катетом – отрезок рулетки от ноля до трех, а гипотенузой – отрезок от трех до восьми метров. Рулетку стараемся держать ближе к поверхности земли – так, чтобы все отрезки по возможности лежали в одной плоскости.
И отрезок между нулем и тройкой (на рисунке синий цвет), и отрезок ленты между тройкой и восьмеркой метровыми отметками (красный) должны быть одинаково хорошо натянуты. Вбиваем колышек В точно в том месте, куда пришлась отметка три метра. Как это все выглядит, видно на рисунке.
Угол САВ будет равен 90 градусам, что и требовалось. Теперь, чтобы построить на местности любой прямоугольник, достаточно отложить длину и ширину на сторонах нашего угла, построить еще один прямой угол.
После построения прямоугольника, для проверки, измерьте его диагонали. Они не должны разниться больше чем на два – три сантиметра при размерах прямоугольника порядка пятнадцати метров.
Определение высоты и глубины на местности, высотные отметки
Теперь узнаем, как определить на местности высоту или глубину. Чтобы дать на местности высотную отметку, в строительстве используют прибор, называемый нивелиром. Но нивелир стоит недешево, да и научиться им пользоваться – дело не пяти минут. Но существует приспособление, точностью не уступающее самым дорогим приборам, а стоимостью равное нескольким батонам хлеба. Называется это чудо техники – гидроуровень. С его помощью можно на расстоянии пятнадцать метров поставить две точки на одинаковую высоту с точностью до двух миллиметров. Принцип гидроуровня основан на законе сообщающихся сосудов, а представляет он собой, в самом простом случае, прозрачную силиконовую трубку диаметром 8 мм, заполненную водой.
К примеру, вам необходимо выполнить бетонный фундамент здания, и, естественно, он должен быть по возможности горизонтальным.
В первую очередь нам нужно определить базовую отметку высоты. Если она не задана в проекте, то назначаем ее произвольно, согласуясь с рельефом, и вбиваем на ней гвоздь. Трубку гидроуровня элементарно затыкаете пальцем, чтобы не вылилась вода; ваш помощник остается возле первого – базового – гвоздя, а вы идете к следующему углу.
Помощник удерживает свой конец уровня вертикально, так чтобы поверхность столбика воды совпала с гвоздем. Вы свой подводите к месту, на котором необходимо указать отметку. Двигая трубку вверх-вниз, помощник добивается совпадения поверхности воды с гвоздем. Ждете, пока вода успокоится, и делаете отметку на опалубке по линии обреза столбика воды. На рисунке это показано достаточно наглядно. В полученную отметку вбиваете второй гвоздь. Так повторяете нужное количество раз. Натянув на вбитые гвозди прочную нить или леску, вы получите строго горизонтальные линии.
Освоив вышеуказанные приемы, комбинируя их, вы сможете осуществлять разбивку на местности весьма сложных конструкций, а также проверку качества их выполнения. Читайте так же о том, как работать тахеометром и нивелиром.
Задавайте вопросы в комментариях ниже либо по почте. Подписывайтесь на новостную рассылку. Успехов вам, и добра вашей семье!chonemuzhik.ru
Как построить прямой угол на земле при помощи простейших инструментов?
Это — древнейшая геометрическая задача.
Пошаговая инструкция
1й способ. — С помощью «золотого», или «египетского», треугольника. Стороны этого треугольника имеют соотношение сторон 3:4:5, а угол равен строго 90град. Этим качеством широко пользовались древние египтяне и другие пракультуры.
Илл.1. Построение Золотого, или египетского треугольника
- Изготавливаем три мерки (или веревочных циркуля – веревка на двух гвоздях или колышках) с длинами 3; 4; 5 метров. Древние в качестве единиц измерения часто пользовались способом завязывания узелков с равными расстояниями между ними. Единица длины — «узелок».
- Вбиваем в точке О колышек, цепляем на него мерку «R3 — 3 узелка».
- Протягиваем веревку вдоль известной границы – в сторону предполагаемой точки А.
- В момент натяжения на линии границы – точка А, вбиваем колышек.
- Затем — снова от точки О, протягиваем мерку R4 – вдоль второй границы. Колышек пока не вбиваем.
- После этого натягиваем мерку R5 – от А до В.
- В месте пересечения мерок R2 и R3 вбиваем колышек. – Это искомая точка В – третья вершина золотого треугольника, со сторонами 3;4;5 и с прямым углом в точке О.
2й способ. С помощью циркуля.
Циркуль может быть веревочный или в виде шагомера. См: …простейший землемерный инструмент
Наш циркуль-шагомер имеет шаг в 1 метр.
Илл.2. Циркуль-шагомер
Построение – также по Илл.1.
- От точки отсчета – точки О – угла соседа, проводим отрезок произвольной длины — но больше, чем радиус циркуля = 1м – в каждую сторону от центра (отрезок АВ).
- Ставим ногу циркуля в точку О.
- Проводим окружность с радиусом (шагом циркуля) = 1м. Достаточно провести короткие дуги – сантиметров по 10-20, в местах пересечения с отмеченным отрезком (через точки А и В.). Этим действием мы нашли равноудаленные точки от центра — А и В. Величина удаления от центра здесь не имеет значения. Можно эти точки просто отметить рулеткой.
- Далее нужно провести дуги с центрами в точках А и В, но несколько (произвольно) большего радиуса, чем R=1м. Можно перенастроить наш циркуль на больший радиус, если он имеет регулируемый шаг. Но для такой небольшой текущей задачи не хотелось бы его «дергать». Или когда регулировки нет. Можно сделать за полминуты веревочный циркуль.
- Ставим первый гвоздь (или ножку циркуля с радиусом больше, чем 1м) поочередно в точки А и В. И проводим вторым гвоздем — в натянутом состоянии веревки, две дуги — так чтобы они пересеклись друг с дружкой. Можно в двух точках: C и D, но достаточно одной – C. И снова хватит коротких засечек на пересечении в точке С.
- Проводим прямую (отрезок) через точки С и D.
- Все! Полученный отрезок, или прямая, — есть точное направление на север :). Простите, — на прямой угол.
- На рисунке показаны два случая несоответствия границы по участку соседа. На Илл.3а приведен случай, когда забор соседа уходит от нужного направления в ущерб себе. На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С.
- Поставьте на углу О колышек, а в точке C — временный колышек, и протяните от С шнур до задней границы участка. – Так, чтобы шнур едва касался колышка О. Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.
Илл.3. Построение прямого угла – от угла соседа, с помощью циркуля-шагомера и веревочного циркуля
Если у Вас есть циркуль-шагомер, то можно и вовсе обойтись без веревочного. Веревочный в предыдущем примере мы применили для проведения дуг большего радиуса, чем у шагомера. Большего потому, что эти дуги должны где-нибудь пересечься. Для того чтобы дуги можно было провести шагомером с тем же радиусом – 1м с гарантией их пересечения, надо чтобы точки А и В находились внутри окружности c R =1м.
- Отмерьте тогда эти равноудаленные точки рулеткой — в разные стороны от центра, но обязательно по линии АВ (линии забора соседа). Чем точки А и В будут ближе к центру – тем дальше от него направляющие точки: C и D, и тем точнее измерения. На рисунке это расстояние принято равным около четверти радиуса шагомера = 260мм.
Илл.4. Построение прямого угла с помощью циркуля-шагомера и рулетки
- Не менее актуальна эта схема действий и при построении любого прямоугольника, в частности — контура прямоугольного фундамента. Вы получите его идеальным. Его диагонали, конечно, нужно проверить, но разве не уменьшаются усилия? – По сравнению, когда диагонали, углы и стороны контура фундамента двигают туда-сюда, пока углы не сойдутся..
Собственно, мы решили геометрическую задачу на земле. Для того чтобы Ваши действия были более уверенными на участке, потренируйтесь на бумаге – с помощью обычного циркуля. Что ничем в принципе не отличается.
www.remotvet.ru
Как построить прямой угол на местности – линейка без прямых углов
Соблюдайте правило прямого угла
Важную информацию о взаимоотношениях людей дает не только расстояние между ними, но и то, под каким углом они стоят или сидят по отношению друг к другу. Оптимальный вариант – это расположение друг к другу под углом 90 градусов.
Правило прямого угла
Мысленно нарисуйте прямоугольный треугольник и представьте, что вы с собеседником стоите на его катетах лицом в центр треугольника. Это открытая позиция. Вы повернуты друг к другу, но перед вами остается свободное пространство для «маневра». Общаясь и постепенно узнавая друг друга, вы сможете доверительно развернуться уже лицом к лицу.
Этот прием всем мужчинам рекомендую использовать при знакомстве с женщиной! Вы должны подойти к ней не лицом к лицу, а сбоку, чтобы между вами образовался угол в 90 градусов. Затем, в процессе беседы, вы можете постепенно разворачивать корпус, чтобы оказаться лицом к лицу, и при этом уменьшать дистанцию между вами. Но только постепенно! Если вы поторопитесь, женщина воспримет это как наглое домогательство. А если будете терпеливы – у вас появится хороший шанс пригласить ее на свидание!
Объяснить действие правила прямого угла проще всего на конкретном примере.
…
Представьте себе, что вы идете по улице, и вдруг к вам обращается человек с просьбой показать, например, какой-то дом. Вы останавливаетесь, чтобы подсказать правильное направление. Куда будет развернут ваш корпус: по направлению движения или к остановившему вас человеку? Правильно: в ту сторону, куда вы и направлялись!
А теперь другой вариант. Снова вы идете по улице и вас окликают, но это – о боже, какая встреча! – ваш старый приятель. Вы останавливаетесь, чтобы поздороваться, перекинуться парой слов и бежать дальше по своим делам. Теперь в какую сторону будет развернут ваш корпус? Конечно же, к приятелю!
В первом случае вы не разворачиваетесь полностью к человеку, потому что он не знаком вам. Ваше подсознание, основная задача которого – биологическая защита, знает, что положение боком по отношению к другому человеку уменьшает площадь поражения при возможном нападении.
Если же мы доверяем собеседнику и хотим с ним общаться, мы неосознанно поворачиваемся к нему – лицом к лицу. Потому что подсознание уверено: угрозы нападения нет.
Так что, если вы хотите найти общий язык с незнакомым собеседником, используйте правило прямого угла – треугольную диспозицию. И почаще обращайте внимание на то, как расположены ваши тела во время общения. Когда вы начинаете доверять друг другу, вы автоматически поворачиваетесь друг к другу лицом к лицу.
Добавлю еще одну маленькую хитрость. Если вы хотите убедить человека в чем-либо, стойте с левой стороны от него – там, где сердце. Доказано, что левая сторона более восприимчива к информации. Неслучайно цыганки на улице, когда подходят погадать, стараются встать с левой стороны, берут левую руку и тихим голосом нашептывают в левое ухо свои предсказания.
Поступайте так же – и будет вам счастье, к гадалке не ходи!
Следите за сигналами собеседника
Вспомните: иногда, общаясь с человеком, вы чувствуете, что он находится будто не с вами, не здесь. Вроде бы человек внимательно слушает вас, кивает головой, улыбается… Но вы ощущаете, что ваши слова пролетают мимо!
Внимание! Посмотрите на расположение тела вашего собеседника. Вы обязательно увидите, что либо поворот корпуса, либо носок ноги вашего партнера указывают в противоположную от вас сторону. Чаще всего к выходу из помещения, в котором вы общаетесь. Или направлены на другого человека, если вы общаетесь втроем.
Знайте: поворот корпуса и направление носка ноги всегда указывает на настоящее направление мыслей вашего собеседника!
Негативные сигналы
Если, проводя переговоры, вы вдруг заметили, что ваш собеседник откинулся назад, чуть отвернул корпус от вас, закинул ногу на ногу и остался в этом положении, срочно меняйте тактику поведения и общения!
Вы ошибаетесь, если думаете, что он расслабился и внимательно вас слушает. Ничуть! Наоборот, вы ему абсолютно неинтересны! Подобное положение тела является закрытым. Оно означает, что ваш собеседник закрылся от вас, удалился в мир своих мыслей.
Такие негативные сигналы могут означать для вас следующее:
• ваш собеседник услышал от вас нечто такое, что ему не понравилось;
• он понял, что ваша идея не представляет для него интереса;
• он уже принял решение отказать вам, не принимать ваше предложение.
Чтобы вновь заинтересовать вашего собеседника, рекомендую протянуть что-нибудь ему в руки. Таким образом он будет вынужден сменить позу, а вы должны использовать этот момент и сменить тактику ведения переговоров!
На что нужно обратить внимание? Во-первых, чтобы удержать внимание партнера, ваши движения и позы должны быть открытыми. Это значит, что ни в коем случае, никогда и ни при каких обстоятельствах, общаясь с людьми, вы не должны скрещивать руки и ноги. Это признак негативного или оборонительного отношения.
Ваша задача – научиться использовать положительные, открытые жесты для успешного общения с другими людьми. И, соответственно, избавиться от жестов закрытых, несущих отрицательную, негативную окраску. Используя открытые жесты, вы будете чувствовать себя более уютно в обществе людей и будете выглядеть более привлекательными для них.
Поза активного слушателя
Если вы хотите быть убедительными и одновременно внимательными к партнеру, обязательно освойте позу «активного слушателя». С ее помощью вы продемонстрируете свою заинтересованность в собеседнике!
Поставьте ноги прямо, параллельно друг другу. Корпус слегка подайте вперед, не откидывайтесь назад. Представьте, что вы слушаете увлекательную историю. Настолько интересную, что вы боитесь упустить даже слово. Поэтому не только ваше тело наклоняется вперед, но и голова слегка подается вперед и немного наклоняется вбок.
Потренируйтесь сперва на своих знакомых, чтобы ваши движения выглядели естественно. А оттачивать мастерство можно на совещаниях, собраниях и деловых встречах!
Концентрируйтесь на позитиве!
Чтобы все описанные выше приемы действовали наиболее эффективно, они должны выглядеть естественными.
Привязка зданий и сооружений к местности, разметка дома
Для этого ваше тело должно реагировать идеально в соответствии с вашими замыслами.
Как этого добиться? Самое простое – вспомнить такое состояние, когда вы чувствовали себя наиболее комфортно. Например, припомните, когда последний раз вы общались с близкими друзьями. Или сидели у камина на кресле-качалке под клетчатым пледом, с интересной книжкой в руках и мурлыкающей кошкой на коленях.
Заметили? Ваши губы расплываются в улыбке, взгляд смягчается, ладони раскрываются… Уверяю вас: при этом зрачки ваших глаз расширяются, а тело автоматически поворачивается к источнику тепла и уюта, будь то близкий человек или любимая кошка.
Это состояние нужно запомнить! И ощущение комфорта и уюта использовать при общении с незнакомым для вас человеком. Просто мысленно представьте, что этот человек – ваш друг, тот самый источник тепла и уюта. Вы очень рады его видеть! Ничего больше не требуется: ваше тело автоматически настроится на нужный лад.
Воспоминания о приятных переживаниях общения запускают цепную реакцию: от подсознательного смягчения взгляда до поворота тела. И все это происходит само собой!
Более того, когда вы ведете себя так, будто только что встреченный и пока незнакомый вам человек необычайно вам нравится, вы и в самом деле начинаете проникаться к нему искренней симпатией!
Это одно из правил психологии.
Когда мы верим, что нравимся другому человеку и что он нравится нам – наше поведение делает эти предположения реальностью. И то же самое происходит, когда мы верим, что не нравимся окружающим – это становится правдой!
Как говорил Генри Форд: «Верите ли вы, что не можете, или верите, что можете – вы правы в обоих случаях».
Практика третьего шага
Запомните основные правила!
Обязательно зафиксируйте в памяти основные правила третьего шага. Чтобы лучше их запомнить, рекомендую записать правила на бумаге. Записав, вы точно сможете их запомнить! Запомнив, будете использовать в жизни. А используя эти правила, вы измените не только свое поведение, но и поведение своих собеседников и партнеров!
Напомню, правила простые: сохраняйте дистанцию, используйте треугольную диспозицию, стойте с левой стороны от собеседника и используйте при разговоре открытые жесты.
Наблюдайте за людьми
Поставьте себе задачу каждый день хотя бы 15 минут наблюдать за поведением людей при разговоре. Оценивайте расположение их тел по отношению друг к другу во время разговора, делайте выводы, набирайтесь опыта!
Шаг четвертый. Покажите ваши руки!
stroyvolga.ru
Как точно разметить прямой угол на местности, не имея транспортира?
Как точно разметить прямой угол на местности, не имея транспортира?
В этом случае для построения прямого угла применяется всем известная формула Пифагора — в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Еще такое построение называют quot;египетским треугольникомquot;, так как по такому же принципу строились углы пирамид. Натяните строительный шнур по главному фасаду одной из сторон будущего строения. Эта линия свое положение НЕ меняет. На шнуре, в точке где будет угол постройки привяжите еще один шнур и отойдите с ним в сторону, образуя другую, перпендикулярную сторону строения.На первом шнуре от точки, образующей угол отмерьте 4 метра. От этой же точки, но по другому шнуру отмерьте 3 метра. На совершенно отдельном шнуре зафиксируйте длину (расстояние) 5 метров (можно привязать яркие тесемки). Далее работают 2 человека. Один человек крайнюю точку пятиметрового шнура держит на шнуре главного фасада в точке 4 метра. Другой человекпостарается 5-и метровый шнур дотянуть до точки 3 м на другом шнуре.Вторая сторона на момент построения будет подвижной.Подтяните или отодвиньте боковую сторону так, чтобы крайние точки 5-иметрового и 3-х метрового шнура соединились. А угол между шнуром/линией главного фасада и линией бокового фасада у вас будет прямым, то есть 90 градусов. А по теореме это выглядит так — 4 (16) + 3 (9) = 5 (25) 25 = 25
Ну, если говоря quot;на местностиquot;, Вы предполагаете начертить прямой угол прямо на земле, к примеру размечая границы какого-то участка или фундамента будущего дома, то можно воспользоваться тремя колышками и шпагатом или вервкой, длинна которой кратна 12 метрам.
Говорят, этот метод был известен ещ в древнем Египте, а в его основе так называемое правило quot;золотого сеченияquot;.
quot;Золотое сечениеquot; — это треугольник со сторонами, длинны которых соотносятся, как 3:4:5
Вот так, более подробно, использование этого метода на практике описывается в интернете:
Как правило строили когда делают прямые углы меряют диагонали полученного прямоугольника. Если нужно сделать что-то маленькое, то можно этот прямой угол обвести по прямоугольному предмету. Самый простой способ это произвести замер диагоналей. Можно и с помощью веревки, смотрите какой вариант вам больше подходит.
Возьмите три брусочка (рейки, линейки, металлические полоски, какие-нибудь жесткие дюралевые элементы для строительства). Сделайте в них по два отверстия диаметром 4-6 мм. Расстояния между центрами отверстий должны относиться друг к другу как 3:4:5, (например 60 см, 80 см и 100 см, или 15 см, 20 см, 25 см). Скрепите брусочки винтами (болтами) в треугольник. Получится прямоугольный треугольник с прямым углом между короткими сторонами (катетами). Чем длиннее стороны треугольников тем точнее будет прямой угол. Но, слишком длинные брусочки могут оказаться кривыми, или прогнуться в процессе изготовления или эксплуатации.
Другой вариант: берете три кусочка мягкой проволоки, с тем же соотношением длин, например 3 4 и 5 м, реально где-то на 10-20 см длиннее. На концах проволоки делаете кольца. Вбиваете в землю два колышка (кусочки труб), допустим, сначала на расстоянии ровно 3 м, накидываете кольца на колышки и сделав петлю где-нибудь в средней части проволоки quot;скруткойquot; выбираете излишек длины, чтобы проволока натянулась как можно прямее между колышками. Точно так же натягиваете другую проволоку на колышки с расстоянием между ними 4 м, и третью — с расстоянием 5 м. Теперь, в вершине требующегося прямого угла вбиваете один колышек. На него накидываете концы 3-х и 4-ж метровых проволок. Другие концы этих проволок продеваете в другие колышки, которые держат в руках Ваши помощники. кольца третьей проволоки (5 м) тоже продеваете в эти колышки. Затем помощники расходятся по требуемым направлениям и подбирают положения колышков, которые у них в руках (удерживая их строго вертикально) так, чтобы все три проволоки были натянуты. Когда такое положение достигнуто, угол будет близок к прямому.
Можно и другие соотношения, лишь бы между ними соблюдалась теорема Пифагора, например 5, 12 и 13, или 7,24 и 25.
Отсутствие транспортира вполне компенсирует теодолит.
Ну и не забываем что диагонали прямоугольника равны между собой.
info-4all.ru
Полезная геометрия | Наука и жизнь
В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.Вешаем зеркало
Вы решили повесить в прихожей зеркало. Тут же возникает вопрос: какой минимальной высоты должно быть зеркало, чтобы человек среднего роста мог видеть себя в нём целиком? И ещё: имеет ли при этом значение размер помещения, где будет висеть зеркало? Решение. Предмет и его отражение симметричны относительно плоскости зеркала. Построим в нём изображение человека (рис. 1): АВ — человек, А1В1 — его изображение, точка С — глаз, DE — зеркало. Из рисунка видно, что минимальная высота зеркала приблизительно равна половине роста человека, считая от уровня глаз. При этом высота Е нижнего края зеркала от пола должна быть вдвое меньше расстояния от пола до глаз. Легко понять, что, на каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нём с головы до ног, значит, размер помещения значения не имеет.Завариваем чай
Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше? Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d2).Выдерживаем прямые углы
Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»? Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строи-тельный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.Строим прямой угол на земле
Известен старинный способ постро-ения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ? Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 5. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.Проверяем перпендикулярность стен
Как проверить, перпендикулярны ли друг другу соседние стены в комнате, воспользовавшись верёвкой с узелками из предыдущей задачи? Решение. Если предположить, что стены в комнате вертикальны, а пол горизонтален, то проверку проводят так. От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы (рис. 6). Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный тре-угольник со сторонами 3, 4, 5 — прямоугольный.Отмеряем нужный объём
Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам? Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна (рис. 7). Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно (рис. 8). А можно ли геометрическим способом узнать объём бутылки? Конечно! Для этого надо заполнить бутылку водой чуть меньше чем наполовину (рис. 9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объём бутылки равен сумме найденных объёмов. Для точности можно учесть толщину стенок бутылки.Укрепляем калитку
Прямоугольная калитка (рис. 10, слева) со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать. Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.Выбираем табурет
Если вы решили предыдущую задачу, то без труда определите, на какой табурет (рис. 11) можно сесть без риска оказаться на полу. Решение. Безопасный табурет изображён на правой картинке, так как его сиденье и ножки образуют треугольник.Исправляем ошибку кроя
Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку? Решение. Для исправления ошибки вы можете разрезать один из треугольников, например так, как показано на рис. 12, а затем сложить из него нужный треугольник.Находим середину
Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня? Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести (рис. 13).www.nkj.ru
Как быстро и точно разметить большой участок земли под фундамент сельского дачного дома.
Мы живем в «прямоугольном» мире, в Декартовой системе координат. Все стройматериалы также выпускаются в виде прямоугольных заготовок. От доски до рулонов утеплителя. От кирпичей, до бетонных плит перекрытия. Только сыпучие материалы меряются ведрами, мешками, кубометрами (кстати, тоже прямоугольными…).
Поэтому крайне важно при разметке большого участка земли под фундамент выдержать эту прямоугольность. Хотя сделать это самодеятельному строителю бывает не всегда легко. Но приходится.
Хотя, если знать основополагающие принципы разметки и знать некоторые приемы, сделать это можно и самостоятельно, и даже в одиночку.
Принцип первый: Диагонали у прямоугольника — равны. Если длины диагоналей не равны — значит это НЕ прямоугольник, а что то иное. Ромб, параллелограмм, или вообще фигура не поддающаяся классификации, просто четырехугольник.
Есть однако и исключение. Диагонали равны и у равнобедренной трапеции! Диагонали у нее одинаковые, но она — не прямоугольник! Это тоже полезно знать, и не радоваться раньше времени, добившись равности диагоналей.
Поэтому необходимо применять
Принцип второй: Для гарантированного построения прямого угла надо построить т.н. «египетский» или «золотой» треугольник. Такой треугольник, согласно многократно доказанной теореме Пифагора, имеет стороны 3, 4, и 5 единиц. Т.е. катеты длиной по 3 и 4 единицы, а гипотенуза равна 5 единицам. Такой треугольник ВСЕГДА прямоугольный. Несмотря на то, что бы вы не подразумевали под «единицами» — метры, сантиметры, длину какой то палочки, удавов или попугаев. Главное, что бы единицы для измерения катетов и гипотенузы были одни и те же.
Эти два принципа — необходимы и достаточны для того, что бы правильно, и с достаточной для строительства точностью разметить участок под фундамент дома или что вам надо.
Итак, переходим к практическим упражнениям на местности.
Для этого нам потребуется рулетка (желательно длиной больше диагонали, что бы не пользоваться узелками на веревочках). И прочный и длинный шнурок (веревочка). Шнурка должно быть много. Весьма полезно иметь несколько тугих прищепок, что бы не возиться с колышками.
Кстати, прежде чем приступать к разметке и вообще к проектированию, неплохо бы определиться с типом строения, из чего будут стены и т.д. Дело в том, что материалы выпускаются определенных размеров. И бывает весьма обидно, когда впоследствии при постройке, вам, например, придется аккуратно отпиливать от каждого куска пенопласта «лишних 5 сантиметров». И так — 170 раз подряд… Может проще было делать каркас сразу под имеющиеся в продаже материалы?
Т.е. поинтересуйтесь, а каких ЭТО (из чего вы будете строить дом и отделывать его) бывает типо-размеров? Весьма полезно и с экономической точки зрения — отходов не будет. Ну почти не будет…
После того, как с размерами вы определились, размечают ПЕРВУЮ стену. Неважно какую, фасад, боковую или заднюю. Ее же ориентируют в нужном вам направлении. Причем длину этой стены никак не учитывают, а берут с запасом, минимум по полметра — метру от предполагаемых углов. Там забивают колышки и туго натягивают шнурок. Т.е. мы разметили не саму стену, а только ее НАПРАВЛЕНИЕ и примерное месторасположение.
Для чего это делается? Дело в том, что в дальнейшем вам ведь придется вынимать грунт для устройства фундамента. Если мы вобьем колышек сразу в место предполагаемого угла фундамента, то при выемке грунта колышек попросту упадет.
Кстати, вместо колышков удобнее использовать 1-2 х метровую доску, к которой прибиты два колышка. Тогда в боковой торец доски можно вбивать гвозди в любом месте и очень оперативно двигать шнуров влево — вправо. Таким образом можно разметить фундамент просто идеально, с точностью до миллиметров. Такой способ разметки называется «обноска» и работать с ней значительно удобнее, чем с колышками.
Когда мы натягиваем первый шнурок и намечаем место первой стены, у нас появляется «печка», от которой мы будем плясать.
Вот теперь пришло время определиться с местом, где будет угол фундамента. Вешаем на это место прищепку на шнурок (или забиваем колышек) и отмечаем длину стены. Теперь у нас есть уже целых два угла.
А вот тут начинается самое интересное.
Точно такую же обноску мы делаем и для другой стены, перпендикулярной первой.
На первом шнурке мы отмеряем 3 единицы ( кстати, чем единицы длиннее , тем точнее будет прямой угол). Например, ровно 3 метра. И вешаем в этом месте прищепку.
От места пересечения шнурков (желательно что бы они были почти на одной высоте), отмеряем 4 единицы ( ровно 4 метра в данном случае) и тоже вешаем прищепку.
Измеряем расстояние между 2-мя прищепками (с помощью рулетки и помощника). Оно должно быть равно ровно (!!!) 5 метров. Разумеется, с первого раза вы вряд ли получите такой результат. Если он МЕНЬШЕ, это значит, что угол более острый, чем 90 градусов. Если БОЛЬШЕ 5-ти метров — значит угол больше 90 градусов. В этом случае необходимо сдвинуть один конец второго шнурка в ту или иную сторону. После этого снова отмерить 3 единицы от перекрестка шнурков по первому шнурку и 4 единицы по второму. И снова измерить гипотенузу…
Такие перемещения и измерения делаются несколько раз и в конце концов вы получаете желаемый результат — гипотенуза треугольника равна 5 метрам, и стены у нас (вернее их разметка) расположены строго перпендикулярно.
Теперь мы можем отмерить длину второй стены и повесить прищепку там (или забить колышек. Это будет уже 3-й угол дома. И у нас уже появилась диагональ. (А мы помним, что нам важна не ее абсолютная длина, а равенство диагоналей. )
Поэтому найти место для 4-го угла — дело техники. Устроив обноску надо просто найти место пересечения третьего и четвертого шнурка при условии равенства длин противоположных стен.
Ну вот и готова ВНЕШНЯЯ обноска фундамента. Если фундамент — плита, этого достаточно. А если фундамент ленточный — устраиваю внутреннюю обноску так же как и первую, с учетом ширины ленты фундамента. Разумеется сделать ее гораздо проще, чем внешнюю.
Этот способ разметки фундамента проверен веками.. А в те времена не было калькуляторов и сельские строители понятия не имели о квадратных корнях.
Поэтому считаю нужным рассказать, как я размечал свой фундамент. Напомню, его внешний размер у меня 15 х 12 метров. Диагональ, соответственно 19.21 метр
Рассчитав все на бумаге, я купил нужное количество шнурка и попросту отмерил весь периметр фундамента. А затем, наметив «углы» я перевязал его крест накрест абсолютно равными диагоналями.
Т.е. я сразу пошел от желаемого результата…
Выйдя на местность, я вбил первый колышек в желаемом месте и сориентировал первую стенку. Соответственно вбил колышек в месте второго угла.
Ну а дальше было дело техники. Взял колышек и натянув «паутину» так, что бы была натянута одновременно и «стенка» и диагональ, я нашел место третьего угла. Ну и точно так же — место для четвертого. Вся процедура не заняла и 30 минут. Причем размечал ее фундамент в одиночку.
А выносную обноску я устроил уже сверху фактически размеченного фундамента. После этого убрал свою «паутину», что бы она не мешала работать.
dom.delaysam.ru
Разбивка на местности. Обноска.[Razbivka-na-mestnosti-Obnoska] | Мой загородный дом
Поскольку здания и сооружения на местности имеют прямые углы, попробуем построить такой угол на местности. Нам понадобится: три штыря из проволоки, диаметром 6-8 мм и длиной 40 см, а так же полипропиленовый шпагат- около 15 метров.
Отрежем два куска шпагата – 4м и 5 м.Выберем исходную точку на участке, где у нас планируется один из углов будущего сооружения. Возьмём один штырь, привяжем к нему оба куска шпагата и воткнём штырь в нашу исходную точку. Это и будет вершина первого прямого угла.
Затем рулеткой отмеряем на длинном куске шпагата ровно 4 м.На этом месте привязываем ещё один штырь.
Теперь на коротком куске шпагата отмеряем ровно 3 м и, точно так же, привязываем третий штырь.
У нас получилось, что один штырь воткнут в исходной точке, и к нему привязаны 2 отрезка шпагата- 3 и 4 м со штырями на концах. Берём третий отрезок шпагата и привязываем его к одному из не воткнутых в землю штырей. От штыря по этому отрезку отмеряем ровно 5 м и завязываем на этой отметке узелок.
Получился простейший, но довольно точный инструмент для построения прямых углов на местности.
Как им пользоваться? Воткнём в землю второй штырь. Обычно это штырь с четырёхметровым отрезком шпагата. Ориентируем его так, как пойдет длинная стена нашего будущего сооружения. Далее, совмещаем место 5и метровой отметки и место третьего штыря, как показано на рисунке 1.
Получился прямой угол на местности.
Таким же образом строим весь прямоугольник будущего сооружения. Теперь правим его диагональю.
Допустим, наше сооружение имеет размер по осям 6м на 8 м.Рассчитаем размер диагонали Д.
Д=6*6+8*8=36+64=100
Извлекаем корень квадратный из 100, получим 10 м
Берём отрезок шпагата чуть более 10м и двумя узелками отметим 10 м. Проверим диагонали, как показано на рисунке 2.
Если диагонали не попадают в углы, переставим штыри. Таким образом, мы вынесли план будущего сооружения в осях.
Выполнение обноски
myzagdom.ru
Как расположить под прямым углом в строительстве
Выложить точные прямые углы на строительных проектах, таких как фундаменты под навесы, настилы или террасы , легко, если вы используете геометрию.
Согласно теореме Пифагора, квадрат двух сторон треугольника, примыкающих к прямому углу (катеты), равен квадрату третьей стороны (гипотенузы). Математически это выражается как a² + b² = c².
Для использования умножьте длину каждого катета треугольника на себя, затем сложите две суммы вместе, чтобы найти длину гипотенузы, когда угол равен 90 °.
Самый простой способ сделать это — использовать метод 3-4-5:
- Отмерьте 3 фута от угла, который вы хотите сделать 90 ° в одном направлении.
- Отмерьте 4 фута от угла, который вы хотите сделать 90 ° в другом направлении.
- Измерьте поперек двух точек и отрегулируйте угол так, чтобы расстояние на третьей стороне треугольника составляло 5 футов.
Вы также можете использовать числа, кратные 3-4-5, в том же соотношении (например, 6, 8, 10) для образования больших или меньших прямых углов.
Посмотрите это видео, чтобы узнать больше.
Дополнительная литература
ВИДЕО ТРАНСКРИПТ
Джо Труини: Вы, возможно, не думали, что когда-нибудь дойдете до использования геометрии средней школы, но если вам когда-либо приходилось выкладывать линии идеально квадратными, под углом угол, вот шанс его использовать.
Если это такой большой проект, как этот, где мы расширяем внутренний дворик, квадрат обрамления был бы слишком маленьким; это было бы недостаточно точно. Итак, мы собираемся использовать теорему Пифагора, основанную на соотношении три, четыре, пять.
Итак, вдоль одной линии я измерил и отметил три фута, а вдоль пересекающейся линии я сделал то же самое, только на четырех футах. А теперь, чтобы применить теорему на практике, вы просто измеряете поперек двух линий и перемещаете кол, внутрь или наружу, пока пятиметровая отметка не совпадет с отметкой, сделанной вами на этой линии. Потом можно вбивать ставку.
И он не будет идеально выровнен в первый раз, но вы можете перемещать ставку внутрь или наружу, из стороны в сторону, как вам нужно.
И это работает — здесь я сделал это на трех, четырех и пяти футах. Но вы можете использовать любое из этих соотношений, например, шесть, восемь или 10. Чем крупнее проект, тем больше числа, тем точнее он будет.
Получение квадрата с треугольником 3: 4: 5
Этот пост может быть немного математическим ботаником, но иногда в строительстве математический ботаник — это тот, кто делает разницу между падением здания и тем, которое длится сто лет. Старые дома заброшены…] Читать далее Пост «Получение квадрата с треугольником 3: 4: 5» первым появился в блоге Craftsman.
Известно, что в старых домах отсутствуют прямые углы. С годами они менялись и оседали, и все не ровно и не ровно. Но я научу вас, как это исправить.
Признаюсь, математика не была моим лучшим предметом в школе. Я гораздо более наглядный человек, и страница, полная цифр, никак не влияет на мое художественное чутье. Но был один курс математики, который имел для меня некоторый смысл.Геометрия. При строительстве и реконструкции геометрия может быть вашим лучшим другом. (Прошу прощения, если это начинает звучать как особенное после школы.)
Вы помните теорему Пифагора? ? Я тоже. Но треугольник 3: 4: 5 для непрофессионала заменяет теорему Пифагора. Треугольник 3: 4: 5 — лучший из известных мне способов определить с абсолютной уверенностью, что угол составляет 90 градусов. Это правило гласит, что если одна сторона треугольника имеет размер 3, а соседняя сторона — 4, то диагональ между этими двумя точками должна иметь размер 5, чтобы он был прямоугольным.Еще не запутались?Это может быть 3 мм, 3 дюйма, 3 фута или 3 мили. Неважно, какую единицу измерения вы используете, пока вы придерживаетесь соотношения 3: 4: 5. И вы также можете использовать кратные 3: 4: 5, например 6: 8: 10 или 9:12:15. Используйте то, что хотите, хотя 3: 4: 5 легче всего запомнить.
Строите колоду, обрамляете стену, кладете плитку? Почти каждый строительный объект в какой-то момент требует прямых углов. А с треугольником 3: 4: 5 вы можете найти свои прямые углы без каких-либо сложных вычислений.
Выберите одну ногу вашего проекта и отмерьте 3 фута от угла. Отметьте на доске отметку в 3 фута. Теперь измерьте соседнюю доску от того же угла до 4 футов и поставьте там отметку. Затем измерьте расстояние между двумя отметками. Если это 5 футов, то у вас идеально квадратный угол. Поздравляю! Если размер меньше 5 футов, угол слишком мал (<90 градусов) и его необходимо немного увеличить. Если он больше 5 футов, угол слишком большой (> 90 градусов) и его необходимо немного закрыть.
Этот удобный трюк убережет вас от серьезных ошибок в будущем. Я знаю, что это самый полезный математический элемент, кроме 1 + 1 = 2, и я использую его почти каждую неделю. Надеюсь, теперь вам не придется гадать, правильны ли ваши проекты. Используя треугольник 3: 4: 5, вы можете знать наверняка.
Какие еще полезные математические приемы вы используете в строительстве, о которых мы могли не знать?
Как построить угол 90 градусов с помощью циркуля и линейки или линейки
На этой странице мы покажем, как построить (нарисовать) угол в 90 градусов с помощью циркуля и линейки или линейки.Есть разные способы сделать это, но в этой конструкции мы используем свойство Теорема Фалеса. Создаем круг, в котором вершина искомого прямого угла — это точка на окружности. Теорема Фалеса гласит, что любой диаметр круга подает под прямым углом к любой точке окружности.
Пошаговые инструкции для печати
Вышеупомянутая анимация доступна как распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.
Объяснение метода
Фактически это та же конструкция, что и при построении перпендикуляра в конечной точке луча. Другой способ сделать это —Проба
Эта конструкция работает с использованием теоремы Фалеса. Он создает круг, где вершина нужного прямого угла является точкой на окружности.
| Аргумент | Причина | |
|---|---|---|
| 1 | Отрезок AB равен диаметру центра окружности D | AB — прямая линия, проходящая через центр. |
| 2 | Угол ACB имеет размер 90 °. | Диаметр окружности всегда образует угол 90 ° с любой точкой (C) на окружности. См. Теорему Фалеса. |
— Q.E.D
Попробуйте сами
Щелкните здесь, чтобы распечатать рабочий лист, содержащий две проблемы, которые можно попробовать. Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатная продукция не защищена авторскими правами.Другие конструкции, страницы на сайте
Строки
Уголки
Треугольники
Правые треугольники
Центры треугольника
Окружности, дуги и эллипсы
Полигоны
Неевклидовы конструкции
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
ручных инструментов — Как сделать квадрат без квадрата?
Я только начинаю работать с деревом, и, поскольку у меня еще нет проекта, который я хотел бы завершить, я заинтересован в создании многих инструментов, которые я бы использовал в процессе обучения (молотки, квадраты , маркер и т. д.).
Так я учусь работать с деревом, а потом и с металлом. Это хороший способ. Строительство квадратов — это красивый маленький проект.
Так как же сделать квадрат без квадрата?
Вы правы в том, что на первый взгляд здесь возникает проблема курицы и яйца.
Можно сделать точный квадрат, не имея точного квадрата для его проверки, но вам нужны вещи, которые должны быть прямым .
Предположим, вы можете получить два куска дерева, у которых есть хотя бы одна плоская прямая сторона. Это будут внешние стороны вашего квадрата. Одним из кусочков нарисуйте прямую горизонтальную линию на чем-нибудь плоском.
Временно соедините две части вместе так, чтобы они все еще могли вращаться относительно друг друга — например, проденьте в них один винт, один дюбель или что-то еще. Сделайте их как можно более квадратными. Затем поместите одну сторону вдоль линии, которую вы только что нарисовали, с квадратом, расположенным как буква L, и используйте новый квадрат, чтобы нарисовать перпендикулярную линию. Теперь переверните все это на так, чтобы теперь это была обратная L, и попытайтесь провести точно такую же перпендикулярную линию.Если квадрат получился точным, перпендикуляры совпадут. Если это не так, вы можете оценить, насколько далеко от квадрата находится ваш квадрат, отрегулируйте его и попробуйте снова.
Продолжайте делать это, пока не получите что-то настолько близкое к квадрату, насколько вы хотите, и вставьте еще один фиксатор в квадрат, чтобы он больше не мог вращаться, и эй, у вас есть точный квадрат, построенный только из точного прямая линия.
Теперь, конечно, возникает вопрос: «Как мне построить точную прямую линию?» Но это другой вопрос.
Как они были первоначально изготовлены, если точность должна быть правильной, но современные методы измерения и производства недоступны.
Вы не говорите, как далеко вы хотите уйти в историю. Способы, которыми древние египтяне добивались квадратной формы строительных блоков, сильно отличаются от способов, которыми средневековые плотники строили квадратные здания, и они сильно отличаются от методов, используемых для создания квадратных точных станков во время промышленной революции.Уточните свой вопрос, если вас интересует история создания инструмента.
Я смотрел много видео Пола Селлерса на YouTube, и они меня подстегнули.
woodgears.ca — тоже хороший сайт для такого рода вещей; там есть видео о том, как сделать свои собственные пробные квадраты, обрамлять квадраты и так далее.
Как найти углы прямоугольного треугольника
Обновлено 3 ноября 2020 г.
Крис Дезил
Сложите значения трех углов в любом треугольнике, и вы получите 180 градусов.Если у вас прямоугольный треугольник, один из его углов по определению равен 90 градусам. Это означает, что сумма двух других углов должна составлять 90 градусов, и если вы знаете один из них, вы можете сразу найти другой. Но как найти углы, если вы тоже не знаете? Ответ заключается в том, чтобы полагаться на другое важное свойство треугольника — длину его сторон. Они связаны с величиной углов.
TL; DR (слишком длинный; не читал)
Найдите углы в прямоугольном треугольнике, вычислив их синус, косинус или тангенс, которые являются функциями длин сторон треугольника.
Синус, косинус и тангенс
Когда вы выбираете, какой из двух углов (ø) в прямоугольном треугольнике вы хотите найти, вы устанавливаете три стороны по отношению к нему. Линия, которая касается угла и продолжается до угла 90 градусов, называется стороной , прилегающей к , а сторона, противоположная углу, — стороной , противоположной стороне . Гипотенуза всегда находится на стороне, противоположной прямому углу. Основываясь на этих определениях, математики используют три соотношения, которые определяют угол в терминах длин сторон:
Синус (sin) — это отношение противоположной стороны к гипотенузе:
\ sin ø = \ frac {\ text {напротив}} {\ text {hypotenuse}}
Косинус (cos) — это отношение смежной стороны к гипотенузе:
\ cos ø = \ frac {\ text {смежный} } {\ text {hypotenuse}}
Касательная (tan) — это отношение противоположной стороны к смежной стороне:
\ tan ø = \ frac {\ text {противоположный}} {\ text {смежный }}
Каждое отношение каждой пары линий соответствует определенному углу, и эти отношения сведены в таблицу вместе с углами, которые они определяют.Если вы можете измерить длину хотя бы двух сторон прямоугольного треугольника, все, что вам нужно сделать, это вычислить синус, косинус или тангенс угла и использовать таблицу, чтобы найти его.
Лестница у стены
Одно из наиболее известных практических применений этих принципов — лестница, опирающаяся на вертикальную стену. Величины углов, которые лестница образует с землей и стеной, имеют решающее значение. Если угол относительно стены слишком мал, лестница упадет назад, а если угол на земле слишком мал, лестница соскользнет.Поскольку угол между стеной и землей составляет 90 градусов, вы можете рассчитать два угла, которые образует лестница, используя синус, косинус или тангенс, и таким образом вы можете предотвратить несчастный случай.
Лестница образует гипотенузу прямоугольного треугольника.
Это расстояние является соседней стороной при определении угла лестницы относительно земли.
Используйте таблицы косинусов, чтобы найти угол между лестницей и землей. Вычислите отношение соседней стороны к гипотенузе, а затем найдите это отношение в таблице косинусов, чтобы найти соответствующий угол.
Рассчитайте угол между лестницей и стеной, вычтя найденный угол из 90. В качестве альтернативы вы можете найти значение этого угла с помощью таблицы синусов.
Пример
20-футовая лестница упирается в стенку дома, а расстояние от основания лестницы до фундамента составляет 12 футов. Каковы углы лестницы относительно земли и дома?
Вычислите косинус угла между лестницей и землей.Это
\ frac {12} {20} = 0,6
Используя таблицу косинусов (или научный калькулятор), вы обнаружите, что угол составляет почти точно 53 градуса. Это делает угол лестницы относительно стены
90 — 53 = 36 \ text {градусы}
Точное измерение углов и расстояний до модели
Что отличает прочную конструкцию и дизайн от M.C. Оптическая иллюзия Эшера? Точные измерения.
В SketchUp инструменты «Рулетка», «Транспортир» и поле «Измерения» позволяют точно моделировать:
Помимо этих инструментов, вы также можете объединить советы из этой статьи с небольшой математикой, чтобы точно оценить высоту здания.
Измерение расстояния
Инструмент «Рулетка» может измерять расстояние, создавать направляющие или отображать координаты по оси x. Вот где вы найдете рулетку в интерфейсе SketchUp:
- Панель инструментов «Начало работы»
- Строительный инструмент
- Панель инструментов большого набора инструментов
- Меню инструментов в строке меню
- Палитра инструментов (macOS)
Совет: Выбрав инструмент «Рулетка», вы можете сразу увидеть длину линии или площадь лица.Наведите курсор рулетки на линию или грань, и вы увидите расстояние или площадь в поле «Измерения».
Чтобы измерить геометрию или установить направляющую линию, выполните следующие действия:
Примечание: Хорошее правило, которое следует запомнить; Вы будете использовать конечные точки для создания направляющих , точек , вы можете создать направляющие , линии , используя средние точки, линии или грани.
- Выберите инструмент Рулетка () или нажмите кнопку T .
Примечание. По умолчанию инструмент «Рулетка» настроен на создание направляющих линий и направляющих точек во время измерения.В режиме создания направляющих рядом с курсором рулетки появляется знак плюса (). Если вы хотите просто измерить между двумя точками без создания направляющей, вы можете нажать Ctrl (Microsoft Windows) или Option (macOS). В этом режиме значок «плюс» рядом с инструментом «Измерить» исчезает. Этот режим будет действовать до тех пор, пока вы не переключите инструменты. - Щелкните начальную точку измерения. Если вам нужно выбрать конечную или среднюю точку, механизм вывода SketchUp поможет вам найти ее. Чтобы создать направляющую линию, щелкните линию, которая должна быть параллельна вашей направляющей линии.
- Переместите курсор в направлении, которое вы хотите измерить. Когда вы перемещаете мышь, временная линия измерительной ленты со стрелками на каждом конце тянется от вашей начальной точки, как показано на рисунке. Совет: Вот несколько советов, которые помогут вам перемещать курсор рулетки в трехмерном пространстве:
- Линия измерительной ленты меняет цвет в соответствии с цветами оси, когда она параллельна любой оси. На рисунке вы видите измерительную ленту, выровненную по красной оси.
- Нажмите и удерживайте кнопку направления во время измерения, чтобы заблокировать ось.Стрелка вверх блокирует синюю ось, стрелка влево блокирует зеленую ось, а стрелка вправо блокирует красную ось.
- В поле «Измерения» динамически отображается длина вашей измерительной ленты.
- Нажмите Esc , если вам нужно начать все сначала.
- (необязательно) Чтобы создать направляющую линию, нажмите Ctrl (Microsoft Windows) или Option (macOS). Рядом с курсором рулетки () появится знак плюса.
- Щелкните в конечной точке измерения. Расстояние от начальной точки отображается в поле «Измерения». Если вы нажали Ctrl на предыдущем шаге, направляющая линия появится в виде пунктирной линии, которая проникает в бесконечное трехмерное пространство (по крайней мере, в вашей модели). На следующем рисунке указатели отмечают расстояние 3 фута от внутренних стен. (См. Раздел Добавление текста в модель для получения информации о маркировке расстояний в вашей модели.)
- (Необязательно) Чтобы переместить направляющую линию на точное расстояние от начальной точки, введите число и единицу измерения, а затем нажмите . Введите .
Совет: При измерении от конечной точки и создании направляющей SketchUp создает направляющую точку, как показано на рисунке. Направляющая точка — это конечная пунктирная линия, а направляющая линия — бесконечная.
Измерение угла
Измерьте угол, если вы хотите продублировать этот угол в другом месте модели или создать планы, например, для проекта деревообработки. Чтобы измерить угол или создать наклонные направляющие линии, используйте инструмент Транспортир.
Инструмент Транспортир () находится в нескольких частях интерфейса SketchUp:
- Строительный инструмент
- Панель инструментов большого набора инструментов
- Меню инструментов
- Палитра инструментов (macOS)
На видео вы увидите, как измерять углы и устанавливать направляющие с помощью инструмента Транспортир. Чтобы узнать, как пройти через этот процесс, прочтите оставшуюся часть этого раздела.
Чтобы измерить угол и создать наклонную направляющую линию, выполните следующие действия:
- Выберите инструмент Транспортир ().Курсор изменится на транспортир. Центральная точка зафиксирована на курсоре.
- Щелкните, чтобы задать вершину угла, который нужно измерить. (См. Выноску 1 на рисунке.) Если вам нужно заблокировать ориентацию, нажмите и удерживайте клавишу Shift перед тем, как щелкнуть.
Совет: Когда вы нажимаете и удерживаете клавишу Shift, чтобы заблокировать / ограничить плоскость вращения, вы можете нажать Alt (Microsoft Windows> или Command (macOS), чтобы освободить транспортир от предполагаемой плоскости. Угол транспортира будет остается углом исходной плоскости, но теперь вы можете перемещать транспортир, чтобы вывести другую геометрию.
- Щелкните в том месте, где начинается угол, который вы хотите измерить. (См. Выноску 2 на рисунке.)
Совет: Вы можете щелкнуть и перетащить от вершины к первой точке, чтобы определить ось вращения. Это особенно полезно, если вам нужно вращать по оси, которая не находится в красной, зеленой или синей плоскостях. Нажмите Esc в любой момент, чтобы начать все заново.
- Переместите курсор, чтобы измерить угол. (См. Выноску 3 на рисунке.) Совет: Вот несколько советов, которые помогут вам найти измерение прямого угла:
- При перемещении курсора угол динамически отображается в поле «Измерения».
- Когда курсор находится близко к транспортиру, угол привязывается к делениям транспортира, которые показывают приращение 15 градусов. Когда ваш курсор находится дальше от центра транспортира, вы можете измерить угол более точными измерениями.
- Щелкните, чтобы установить наклонную направляющую линию.
- (Необязательно) Введите значение и нажмите Введите , чтобы изменить угол направляющей линии (относительно начальной линии). Вы можете ввести десятичное значение, например 34.1 , или наклон, например 1: 6 . Измените это значение сколько угодно раз, пока не сделаете другой выбор или не выберете другую команду.
Примечание. SketchUp может обрабатывать до 0,1 градуса угловой точности.
Редактирование направляющих линий
Чтобы изменить ориентацию направляющей линии или направляющей точки, вы можете переместить или повернуть ее. Подробности см. В разделах «Перемещение объектов вокруг» и «Переворачивание и вращение».
Примечание: Вы не можете изменить размер направляющей линии, потому что направляющие линии бесконечны по длине.
Скрытие и стирание направляющих линий
Направляющие обычно создаются как временное вспомогательное средство для построения части вашей модели. Сохранение слишком большого количества направляющих линий в вашей модели может снизить точность вывода SketchUp и производительность отображения, поэтому вы можете скрыть направляющие линии во время работы или удалить все направляющие линии после завершения 3D-модели.
Чтобы скрыть направляющие линии, вы можете использовать один из следующих методов:
- С помощью инструмента Select () выберите одну или несколько направляющих, а затем выберите Edit> Hide .
- Щелкните контекстным щелчком выбранную направляющую или направляющие и выберите Hide из появившегося меню, как показано на рисунке.
Чтобы снова сделать скрытые направляющие видимыми, выберите Правка> Показать и выберите параметр в подменю «Показать».
Удаление направляющих линий полностью удаляет их и больше никогда не будет. Вот несколько способов удалить направляющие линии:
- С помощью инструмента Select () выберите одну или несколько направляющих, а затем выберите Edit> Delete .
- Щелкните руководство и выберите Стереть в появившемся меню.
- Щелкните направляющую линию с помощью инструмента Eraser ().
- Выберите Правка> Удалить направляющие , чтобы удалить все направляющие в текущем контексте.
Точная оценка высоты здания
Если вы не знаете высоту существующего здания, которое пытаетесь смоделировать, вот несколько методов, которые вы можете использовать, чтобы сделать обоснованное предположение:
- Подсчитать повторяющиеся единицы.
- Сделать снимок с объектом известной высоты
- Использовать тригонометрию.
Когда вы будете готовы выдавить контуры здания до нужной высоты, убедитесь, что вы находитесь в представлении ISO, выбрав Камера> Стандартные виды> ISO . Затем используйте инструмент Push / Pull (), чтобы выдавить здание в 3D и ввести точную высоту здания.
Метод 1. Подсчет повторяющихся единиц
Часто здания строятся из кирпича, блоков или других модульных строительных материалов.Измерьте высоту одного блока, подсчитайте общее количество блоков на фасаде и умножьте его, чтобы получить приблизительную общую высоту.
Этот метод также работает для всех уровней здания. Если вы можете измерить один уровень на фасаде вашего здания, вы можете умножить его на общее количество уровней, чтобы получить приблизительное общее измерение.
Способ 2. Сделайте снимок объекта известной высоты
Когда вы делаете снимок здания, которое планируете смоделировать, включите на снимок что-нибудь (или кого-нибудь), высота которого вам известна.
Совет: Вот несколько советов по оценке высоты здания с помощью этого метода:- Метрная палка или человек работает хорошо.
- Для точности разместите «известное количество» как можно ближе к зданию.
- Сделайте снимок как можно дальше, чтобы минимизировать вертикальное искажение.
Вы можете использовать программу редактирования фотографий, чтобы оценить высоту вашего здания на основе объекта (или человека), который вы включили в фотографию.
Метод 3. Используйте простую тригонометрию
С помощью нескольких простых измерений можно с некоторой точностью оценить высоту. Взгляните на рисунок ниже. Все, что вам нужно знать:
- Ваше расстояние от дома
- Высота ваших глаз
- Угол между землей и верхом здания
Используйте эту формулу для расчета высоты здания:
Высота = (загар (угол) x расстояние) + высота глаз
Например, при расстоянии до здания 25 метров, угле 37 градусов и высоте глаз 1.75 метров, формула будет такой:
Высота = коричневый (37) x 25 м + 1,75 м
= 0,75355 x 25 м + 1,75 м
= 20,6 м
Примечание: На вашем калькуляторе кнопка загара вычисляет тангенс угла.
Краткий справочник измерительной коробки
В этом разделе вы найдете таблицы, в которых перечислены все значения, которые принимает поле «Измерения», в зависимости от того, какой инструмент вы используете. Помните, что после использования инструмента вы можете просто ввести значение и нажать Введите .Вам не нужно нажимать на поле «Измерения». Кроме того, пока вы не внесете еще одно изменение в свою модель или не выберете другой инструмент, вы можете продолжать вводить значения, которые изменяют ваше действие.
Указание единиц измерения
В следующей таблице показано, как указать единицы измерения. Если вы не укажете единицу измерения, SketchUp будет использовать единицы из вашего шаблона. Чтобы просмотреть или изменить единицы измерения по умолчанию, выберите Окно > Информация о модели и выберите Единицы на боковой панели слева.
| Установка | Как это указать | Пример |
|---|---|---|
| дюймов | Номер+ « | »10 дюймов |
| футов | Номер+ ’ | 10 ’ |
| Миллиметры | Номер+ | мм10 мм |
| Сантиметры | Номер+ см | 10 см |
| Метры | Номер+ м | 10 мес. |
Создание массивов
Массив выстраивает геометрию в линию (линейный массив , ) или вокруг точки (радиальный массив , ).Вы создаете массив, когда копируете геометрию с помощью инструмента «Перемещение» или инструмента «Повернуть». В следующей таблице перечислены все модификаторы, которые вы можете использовать при создании массивов.
| Тип массива | Как это указать | Пример | Шаг |
|---|---|---|---|
| Внешний | Номер+ x | 3x | Равное расстояние как у оригинала, так и у исходной копии |
| Внешний | Номер+ * | 3 * | Равное расстояние как у оригинала, так и у исходной копии |
| Внутренний | Номер+ / | 3/ | Равное расстояние между оригиналом и исходной копией |
Ввод значений измерений для конкретного инструмента
Сразу после использования инструмента вы можете ввести точные значения, которые появятся в поле «Измерения».Значения, которые вы можете ввести, зависят от инструмента.
Примечание: Точный формат разделителя списка может отличаться в зависимости от региональных настроек вашего компьютера. Для европейских пользователей символ разделителя списка может быть точкой с запятой вместо запятой.
Следующие ссылки указывают на статью, в которой описаны допустимые значения и модификаторы для каждого инструмента:
Поворачивая путь майя под прямым углом
Великая пирамида майя Кукулькан «Эль-Кастильо», вид с платформы Орлов и Ягуаров, Чичен-Ица, Мексика.
Как построить прямой угол, если у вас нет способа измерить углы? Один очень хитрый способ исходит от народа майя. Классический период майя длился примерно с 250 по 900 год нашей эры. За это время майя построили сотни городов на территории, простирающейся от нынешней южной Мексики через полуостров Юкатан до западного Гондураса и Сальвадора, включая те, что сейчас являются Гватемалой и Белизом. Мы узнали о трюке с прямым углом от Кристофера Пауэлла из Исследовательского центра майя.
На лекции во время ознакомительной поездки MAA 2011 Пауэлл объяснил, что слышал об этой технике от мастера-строителя, который изучил ее, будучи учеником шамана. Вы начинаете с шнура, на котором есть восемь узлов, и делите его на семь равных отрезков с узлом на каждом конце. На каждом узле есть петли для привязки к земле.
Поскольку узлы расположены равномерно, когда узлы 1 и 4 удерживаются вместе и шнур натянут, образуется равносторонний треугольник с внутренними углами 60 °.Затем узел 6 соединяется с узлом 3, и шнур туго натягивается, в результате чего образуется еще один равносторонний треугольник, образованный узлами 4, 5 и 6. Наконец, узел 8 соединяется с узлом 5, образуя третий равносторонний треугольник (и все вместе — половину шестиугольника). . Если провести луч (или веревку) от узла 1 до узла 2, а другой луч — от узла 1 до узла 7, полученный угол будет прямым (60 ° + 30 °). На анимации ниже (созданной Джоном К. Д. Диамантопулосом) показано, как образуется прямой угол.
Джон К.Д. Диамантопулос также создал следующее видео с участием студентов-добровольцев, чтобы продемонстрировать способ майя формировать прямой угол. См. Здесь подробные инструкции о том, как воссоздать упражнение с учащимися.
Об этой статье
Эта статья впервые появилась в книге Convergence , опубликованной Математической ассоциацией Америки, чтобы помочь учителям преподавать математику с использованием истории математики. Щелкните здесь, чтобы увидеть все ресурсы, относящиеся к геометрии майя, опубликованные на Convergence .
Джон К. Д. Диамантопулос — профессор кафедры математики и информатики Северо-Восточного государственного университета в Талекуа, штат Оклахома. Он был очень активен в MAA, как на уровне секции, так и на национальном уровне. Его математические интересы включают обыкновенные дифференциальные уравнения, математическое образование и историю математики. Диамантопулос также очень активен в своей церкви, работая волонтером в компьютерной продукции / презентациях и в любой области, требующей внимания.
Синтия Дж.