Как сложить число и корень – Как сложить корень и число 🚩 y равен корень из x 🚩 Математика

Как сложить корень и число

Арифметическим корнем n-й степени из действительного числа a называют такое неотрицательное число x, n-я степень которого равна числу a. Т.е. (√n) a =x, x^n = a. Существуют различные способы сложения арифметического корня и рационального числа. Здесь для большей наглядности будут рассмотрены корни второй степени (или квадратные корни), объяснения будут дополнены примерами с вычислением корней других степеней.

Пусть задано выражения вида a + √b. Первое, что нужно сделать, — это определить, не является ли число b полным квадратом. Т.е. попробовать найти такое число c, что c^2 = b. В этом случае вы извлекаете квадратный корень из числа b, получаете число c и складываете его с числом a: a + √b = a + √(c^2) = a + с. Если вы имеете дело не с квадратным корнем, а с корнем n-й степени, то для полного извлечения числа b из под знака корня необходимо, чтобы это число было n-й степенью некоторого числа. Например, число 81 извлечется из под квадратного корня: √81 = 9. Также оно извлечется из под знака корня четвертой степени: (√4) 81 = 3.

Обратите внимание на следующие примеры.

• 7 + √25 = 7 + √(5^2) = 7 + 5 = 12. Здесь под знаком квадратного корня стоит число 25, которое является полным квадратом числа 5.

• 7 + (√3)27 = 7 + (√3) (3^3) = 7 + 3 = 10. Здесь был извлечен кубический корень из числа 27, которое является кубом числа 3.

• 7 + √(4/9) = 7 + √( (2/3)^2 ) = 7 + 2/3 = 23/3. Для извлечения корня из дроби необходимо извлечь корень из числителя и из знаменателя.

Если число b под знаком корня не является полным квадратом, то попробуйте разложить его на множители и вынести множитель, являющийся полным квадратом, из под знака корня. Т.е. пусть число b имеет вид b = c^2 * d. Тогда √b = √(c^2 * d) = c * √d. Или же число b может содержать в себе квадраты двух чисел, т.е. b = c^2 * d^2 * e * f . Тогда √b = √(c^2 * d^2 * e * f)= c * d * √(e * f).

Примеры вынесения множителя из под знака корня:

• 3 + √18 = 3 + √(3^2 * 2) = 3 + 3√2 = 3 * (1 + √2).

• 3 + √(7 / 4) = 3 + √ (7 / 2^2) = 3 + √7 / 2 = (6 + √7) / 2. В данном примере был вынесен полный квадрат из знаменателя дроби.

• 3 + (√4)240 = 3 + (√4) (2^4 * 3 * 5) = 3 + 2 *(√4) 15. Здесь получилось вынести 2 в четвертой степени из под знака корня четвертой степени.

И наконец, если вам необходимо получить приблизительный результат (в случае, если подкоренное выражение не является полным квадратом), воспользуйтесь калькулятором для вычисления значения корня. Например, 6 + √7 ≈ 6 + 2,6458 = 8,6458.

completerepair.ru

Как складывать корни и числа стоящие под корнем?

Для того чтобы дать ответ на этот вопрос- разберем понятие «корень»

Математики такой вот странный «народ».. если придумывают какое то математическое действие — то сразу же придумывают к этому действию обратное
например
сложение — вычитание
умножение — деление

вот и придумав Возведение в степень — появилось обратное действие 
Извлечение корня.. 
если перейти на цифры то

теперь как работать с математическими выражениями которые содержат Корни

как уже говорилось Корень- это математической действие, а значит 
√6 означает что есть число 6 и мы должны выполнить еще одно математическое действие- Извлечь корень (найти такое число, которое в квадрате даст число 6)

что можно делать с числами, стоящими под знаком корень? 
тут все просто: Корень- домик. Если в домике есть жильцы то они Внутри домика могут делать что хотят

и так далее

Могут ли числа выходить из домика? Да.. могут.. но только при одном условии: ЕСЛИ между ними стоит УМНОЖЕНИЕ

НО

ТАК делать нельзя

теперь как складывать корни.. 
Если в «домиках сидят одинаковые числа- значит это ОДИНАКОВЫЕ домики и мы считаем сколько таких домиков
ПРИМЕР

т.е. Домиков с жильцом =5 всего 3. А остальных домиков по одному. И их складывать нельзя
читаем так: домик с 5 + домик с 2 + 2 домика с 5 — домик 4 =3 домика с 5+ домик с 2- домик 4 ( а это =2, т.к. 2²=4)

Если в выражении есть число без домика и отдельно домик= то это совсем разные числа.. как коровы и зайцы… и их складывать (вычитать) нельзя

 
просто выражение и его ни как уже не упростить

 

Оцени ответ

pomogajka.com

Как сложить квадратный корень и обычное число. Снова в школу

Квадратным корнем из числа X называется число A , которое в процессе умножения самого на себя (A * A ) может дать число

X .
Т.е. A * A = A 2 = X , и √X = A .

Над квадратными корнями (√x ), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y ).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.

Шаг 1. Извлечение квадратных корней

Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9 . Первое число 4 является квадратом числа

2 . Второе число 9 является квадратом числа 3 . Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5 .
Все, пример решен. Но так просто бывает далеко не всегда.

Шаг 2. Вынесение множителя числа из-под корня

Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54 .

Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .

В числе 24 мы имеем множитель 4 , его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9 .

Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .

Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.

Шаг 3. Сокращение знаменателя

Рассмотрим следующую ситуацию: сумма двух квадратных корней — это знаменатель дроби, например, A / (√a + √b)

.
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b .

Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a — b .

Аналогично, если в знаменателе имеется разность корней: √a — √b , числитель и знаменатель дроби умножаем на выражение √a + √b .

Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .

Пример сложного сокращения знаменателя

Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.

Для примера берём дробь: 12 / (√2 + √3 + √5) .
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5 .

Получаем:

12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.

Шаг 4. Вычисление приблизительного значения на калькуляторе

Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.

Пример вычисления приблизительного значения

Необходимо вычислить приблизительное значение данного выражения √7 + √5 .

В итоге получаем:

√7 + √5 ≈ 2,65 + 2,24 = 4,89 .

Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.

Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результат

electriclub.ru

Квадратный корень. Подробная теория с примерами.

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Для начала почитай комментарии внизу этой статьи, чтобы понять насколько крутой материал ты сейчас читаешь! )

А теперь давай попробуем разобраться, что это за понятие такое «квадратный корень».

К примеру, перед нами уравнение  .

Какое решение у данного уравнения? Какие числа можно возвести в квадрат и получить при этом  ?

Вспомнив таблицу умножения, ты легко дашь ответ:   и   (ведь при перемножении двух отрицательных чисел получается число положительное)!

Для упрощения математики ввели специальное понятие квадратного корня

и присвоили ему специальный символ  

Давай разберемся с корнем до конца…

СОДЕРЖАНИЕ

---

 

Введение понятия арифметического квадратного корня​

Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа   называется такое неотрицательное число, квадрат которого равен  .  .

А почему же число   должно быть обязательно неотрицательным?

Например, чему равен  ?

Так-так, попробуем подобрать. Может, три? Проверим:  , а не  .

Может,  ? Опять же, проверяем:  .

Ну что же, не подбирается?

Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число!

Это надо запомнить: число или выражение под знаком корня должно быть неотрицательным!

 

Однако ты наверняка уже заметил, что в определении сказано, что «квадратным корнем из числа   называется такое неотрицательное число, квадрат которого равен  ».

А в самом начале мы разбирали пример  , подбирали числа, которые можно возвести в квадрат и получить при этом  , ответом были   и  , а тут говорится про какое-то «неотрицательное число»!

Такое замечание вполне уместно. Здесь необходимо просто разграничить понятия квадратных уравнений и арифметического квадратного корня из числа.

К примеру,   не равносильно выражению  .

Из   следует, что

 , то есть   или  ;   (не помнишь почему так? Почитай тему «Модуль числа»!)

А из   следует, что  .

Конечно, это очень путает, но это необходимо запомнить, что знаки являются результатом решения уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.

В наше квадратное уравнение подходит как  , так и  .

Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.

Итак, вкратце на примере, нужно ли ставить «плюс-минус» (этот наглядный пример привёл наш читатель Игорь, спасибо ему за это):

Пусть есть две ситуации:

1)  

2)  

В первом случае у нас квадратное уравнение и его решением будет   (уже видно отличие от второго случая) и далее получаем два корня  

Во втором случае у нас НЕТ квадратного уравнения, просто х равен корню из числа и в этом случае ответ всегда «одно неотрицательное число», то есть 8.

А теперь попробуй решить такое уравнение  .

Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?

Начнем с самого начала – с нуля:   – не подходит.

Двигаемся дальше  ;   – меньше трех, тоже отметаем.

А что если  ? Проверим:   – тоже не подходит, т.к. это больше трех.

С отрицательными числами получится такая же история.

И что же теперь делать? Неужели перебор нам ничего не дал?

Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между   и  , а также между   и  .

Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.

И что дальше?

Давай построим график функции   и отметим на нем решения.

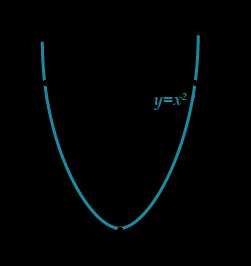
Попробуем обмануть систему и получить ответ с помощью калькулятора! Извлечем корень из  , делов-то!

Ой-ой-ой, выходит, что   Такое число никогда не кончается.

Как же такое запомнить, ведь на экзамене калькулятора не будет!?

Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение.   и   уже сами по себе ответы.

Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.

Рассмотрим еще один пример для закрепления. Разберем такую задачку: тебе необходимо пересечь по диагонали квадратное поле со стороной   км, сколько км тебе предстоит пройти?

Самое очевидное здесь рассмотреть отдельно треугольник и воспользоваться теоремой Пифагора:  .

Таким образом,  .

Так чему же здесь равно искомое расстояние?

Очевидно, что расстояние не может быть отрицательным, получаем, что  . Корень из двух приблизительно равен  , но, как мы заметили раньше,   -уже является полноценным ответом.

Извлечение корней

Чтобы решение примеров с корнями не вызывало проблем, необходимо их видеть и узнавать.

Для этого необходимо знать, по меньшей мере, квадраты чисел от   до  , а также уметь их распознавать.

То есть, тебе необходимо знать, что   в квадрате равно  , а также, наоборот, что   – это   в квадрате.

Первое время в извлечении корня тебе поможет эта таблица.

Как только ты прорешаешь достаточное количество примеров, то надобность в ней автоматически отпадет.

Попробуй самостоятельно извлечь квадратный корень в следующих выражениях:

1.  ;
2.  ;
3.  ;
4.  ;

Ответы:

1.  
2.  
3.  
4.  

 

Ну как, получилось? Теперь давай посмотрим такие примеры:

1.  ;
2.  ;
3.  .

Ответы:

 

1.  ;
2.  ;
3.  .

 

 

 Свойства арифметического квадратного корня

Теперь ты знаешь, как извлекать корни и пришло время узнать о свойствах арифметического квадратного корня. Их всего 3:

• умножение;
• деление;
• возведение в степень.

Их ну просто очень легко запомнить с помощью этой таблицы и, конечно же, тренировки:

Свойство	Пример
Корень произведения равен произведению корней:
Корень из дроби — это корень из числителя и корень из знаменателя:  , если
Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение:  , при

 

Попробуем решить по несколько примеров на каждое свойство!

 

Умножение корней

Взглянул еще раз на табличку… И, поехали!

Начнем с простенького:

 

 

 

Минуууточку.   это  , а это значит, что мы можем записать вот так:

 

 

Усвоил? Вот тебе следующий:

 

 

Корни из получившихся чисел ровно не извлекаются? Не беда – вот тебе такие примеры:

 

 

 

А что, если множителей не два, а больше? То же самое! Формула умножения корней работает с любым количеством множителей:

 

 

Теперь полностью самостоятельно:

1.  
2.  
3.  

 

Ответы: Молодец! Согласись, все очень легко, главное знать таблицу умножения!

1.  ;
2.  ;
3.  .

 

Деление корней

С умножением корней разобрались, теперь приступим к свойству деления.

Напомню, что формула в общем виде выглядит так:

 , если  .

А значит это, что корень из частного равен частному корней.

 

Ну что, давай разбираться на примерах:

 

 

Вот и вся наука. А вот такой пример:

 

Все не так гладко, как в первом примере, но, как видишь, ничего сложного нет.

 

А что, если попадется такое выражение:

 

Надо просто применить формулу в обратном направлении:

 

 

А вот такой примерчик:

 

 

Еще ты можешь встретить такое выражение:

 

 

Все то же самое, только здесь надо вспомнить, как переводить дроби (если не помнишь, загляни в тему дроби и возвращайся!). Вспомнил? Теперь решаем!

 

Уверена, что ты со всем, всем справился, теперь попробуем возводить корни в степени.

 

Возведение в степень

А что же будет, если квадратный корень возвести в квадрат? Все просто, вспомним смысл квадратного корня из числа   – это число, квадратный корень которого равен  .

Так вот, если мы возводим число, квадратный корень которого равен  , в квадрат, то что получаем?

Ну, конечно,  !

Рассмотрим на примерах:

 
 

 

 

Все просто, правда? А если корень будет в другой степени? Ничего страшного!

Придерживайся той же логики и помни свойства и возможные действия со степенями.

Забыл?

Почитай теорию по теме «Степень и ее свойства» и тебе все станет предельно ясно.

Вот, к примеру, такое выражение:

 

В этом примере степень четная, а если она будет нечетная? Опять же, примени свойства степени и разложи все на множители:

 

С этим вроде все ясно, а как извлечь корень из числа в степени? Вот, к примеру, такое:

 

Довольно просто, правда? А если степень больше двух? Следуем той же логике, используя свойства степеней:

 
 

Ну как, все понятно? Тогда реши самостоятельно примеры:

1.  
2.  
3.  

А вот и ответы:

 

1.  
2.  
3.  

 

Внесение под знак корня

Что мы только не научились делать с корнями! Осталось только потренироваться вносить число под знак корня!

Это совсем легко! 

 

 

Допустим, у нас записано число  

Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из  !

 

Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:

 
Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно! Только надо помнить, что вносить под знак квадратного корня мы можем только положительные числа.

Реши самостоятельно вот этот пример —  
Справился? Давай смотреть, что у тебя должно получиться:

 

 

Молодец! У тебя получилось внести число под знак корня! Перейдем к не менее важному – рассмотрим, как сравнивать числа, содержащие квадратный корень!

 

Сравнение корней

Зачем нам учиться сравнивать числа, содержащие квадратный корень?

Очень просто. Часто, в больших и длиииинных выражениях, встречающихся на экзамене, мы получаем иррациональный ответ (помнишь, что это такое? Мы с тобой сегодня об этом уже говорили!)

Полученные ответы нам необходимо расположить на координатной прямой, например, чтобы определить, какой интервал подходит для решения уравнения. И вот здесь возникает загвоздка: калькулятора на экзамене нет, а без него как представить какое число больше, а какое меньше? То-то и оно!

Например, определи, что больше:   или  ?

Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня?

Тогда вперед:

 

 

 

Ну и, очевидно, что чем больше число под знаком корня, тем больше сам корень!

Т.е. если  , значит,  .

Отсюда твердо делаем вывод, что  . И никто не убедит нас в обратном!

 

Извлечение корней из больших чисел

До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!

 

Можно было пойти по иному пути и разложить на другие множители:

 

Что дальше? А дальше раскладываем на множители до самого конца:

 

Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.

Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:

 

Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:

А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):

 

 

Разве это конец? Не останавливаемся на полпути!

 

На простые множители разложили. Что дальше? А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:

 

Вот и все, не так все и страшно, правда?

 

Получилось  ? Молодец, все верно!

А теперь попробуй вот такой пример решить:

 

А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться. Но нам он, конечно, по зубам.

 

Ну что, начнем раскладывать   на множители? Сразу заметим, что можно поделить число на   (вспоминаем признаки делимости):

 

А теперь, попробуй сам (опять же, без калькулятора!):

 

Ну что, получилось  ? Молодец, все верно!

 

Подведем итоги

1. Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа   называется такое неотрицательное число, квадрат которого равен  .
    .
2. Если мы просто извлекаем квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.
3. Свойства арифметического корня:

   Свойство	Пример
   Корень произведения равен произведению корней , если
   Корень из дроби — это корень из числителя и корень из знаменателя. , если
   Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение , при

4. При сравнении квадратных корней необходимо помнить, что чем больше число под знаком корня, тем больше сам корень.

 

Как тебе квадратный корень? Все понятно?

Мы постарались объяснить тебе без воды все что нужно знать на экзамене про квадратный корень.

Теперь твоя очередь. Напиши нам сложная это для тебя тема или нет.

Узнал ты что-то новое или все было и так ясно.

Пиши в комментариях и удачи на экзаменах!

 

Получить доступ к учебнику YouClever без ограничений можно кликнув по этой ссылке:

 ПОЛУЧИТЬ ДОСТУП К УЧЕБНИКУ YOUCLEVER!

 

 

youclever.org

Как складывать квадратные корни

Квадратным корнем из числа X называется число A, которое в процессе умножения самого на себя (A * A) может дать число X. 
Т.е. A * A = A² = X, и √X = A.

Над квадратными корнями (√x), как и над другими числами, можно выполнять такие арифметические операции, как вычитание и сложение. Для вычитания и сложения корней их нужно соединить посредством знаков, соответствующих этим действиям (например √x — √y).
А потом привести корни к их простейшей форме — если между ними окажутся подобные, необходимо сделать приведение. Оно заключается в том, что берутся коэффициенты подобных членов со знаками соответствующих членов, далее заключаются в скобки и выводится общий корень за скобками множителя. Коэффициент, который мы получили, упрощается по обычным правилам.

Шаг 1. Извлечение квадратных корней

Во-первых, для сложения квадратных корней сначала нужно эти корни извлечь. Это можно будет сделать в том случае, если числа под знаком корня будут полными квадратами. Для примера возьмем заданное выражение √4 + √9. Первое число 4 является квадратом числа 2. Второе число 9 является квадратом числа 3. Таким образом, можно получить следующее равенство: √4 + √9 = 2 + 3 = 5. 
Все, пример решен. Но так просто бывает далеко не всегда.

Шаг 2. Вынесение множителя числа из-под корня

Если полных квадратов нет под знаком корня, можно попробовать вынести множитель числа из-под знака корня. Для примера возьмём выражение √24 + √54.

Раскладываем числа на множители:
24 = 2 * 2 * 2 * 3,
54 = 2 * 3 * 3 * 3.

В числе 24 мы имеем множитель 4, его можно вынести из-под знака квадратного корня. В числе 54 мы имеем множитель 9.

Получаем равенство:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6.

Рассматривая данный пример, мы получаем вынос множителя из-под знака корня, тем самым упрощая заданное выражение.

Шаг 3. Сокращение знаменателя

Рассмотрим следующую ситуацию: сумма двух квадратных корней – это знаменатель дроби, например, A / (√a + √b).
Теперь перед нами стоит задача «избавиться от иррациональности в знаменателе».
Воспользуемся следующим способом: умножаем числитель и знаменатель дроби на выражение √a — √b.

Формулу сокращённого умножения мы теперь получаем в знаменателе:
(√a + √b) * (√a — √b) = a – b.

Аналогично, если в знаменателе имеется разность корней: √a — √b, числитель и знаменатель дроби умножаем на выражение √a + √b.

Возьмём для примера дробь:
4 / (√3 + √5) = 4 * (√3 — √5) / ( (√3 + √5) * (√3 — √5) ) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3).

Пример сложного сокращения знаменателя

Теперь будем рассматривать достаточно сложный пример избавления от иррациональности в знаменателе.

Для примера берём дробь: 12 / (√2 + √3 + √5).
Нужно взять её числитель и знаменатель и перемножить на выражение √2 + √3 — √5.

Получаем:

12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.

Шаг 4. Вычисление приблизительного значения на калькуляторе

Если вам требуется только приблизительное значение, это можно сделать на калькуляторе путём подсчёта значения квадратных корней. Отдельно для каждого числа вычисляется значение и записывается с необходимой точностью, которая определяется количеством знаков после запятой. Далее совершаются все требуемые операции, как с обычными числами.

Пример вычисления приблизительного значения

Необходимо вычислить приблизительное значение данного выражения √7 + √5.

В итоге получаем:

√7 + √5 ≈ 2,65 + 2,24 = 4,89.

Обратите внимание: ни при каких условиях не следует производить сложение квадратных корней, как простых чисел, это совершенно недопустимо. То есть, если сложить квадратный корень из пяти и из трёх, у нас не может получиться квадратный корень из восьми.

Полезный совет: если вы решили разложить число на множители, для того, чтобы вывести квадрат из-под знака корня, вам необходимо сделать обратную проверку, то есть перемножить все множители, которые получились в результате вычислений, и в конечном результате этого математического расчёта должно получиться число, которое нам было задано первоначально.

imdiv.com

Правило сложения корней формулы. Как складывать и вычитать квадратные корни

Содержимое:

В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется слева над знаком корня. Выражение, стоящее под знаком корня, называется подкоренным выражением. Сложение корней похоже на сложение членов алгебраического выражения, то есть требует определения подобных корней.

Шаги

Часть 1 Определение корней

1. 1 Обозначение корней. Выражение под знаком корня (√) означает, что из этого выражения необходимо извлечь корень определенной степени.
   • Корень обозначают знаком √.
   • Показатель (степень) корня пишется слева над знаком корня. Например, кубический корень из 27 записывается так: 3 √(27)
   • Если показатель (степень) корня отсутствует, то показатель считается равным 2, то есть это квадратный корень (или корень второй степени).
   • Число, записанное перед знаком корня, называется множителем (то есть это число умножается на корень), например 5√(2)
   • Если множителя перед корнем нет, то он равен 1 (напомним, что любое число, умноженное на 1, равняется самому себе).
   • Если вы впервые работаете с корнями, сделайте соответствующие пометки над множителем и показателем корня, чтобы не запутаться и лучше понять их назначение.
2. 2 Запомните, какие корни можно складывать, а какие нельзя. Также, как нельзя складывать разные члены выражения, например, 2а + 2b ≠ 4ab, вы не можете складывать разные корни.
   • Нельзя складывать корни с разными подкоренными выражениями, например, √(2) + √(3) ≠ √(5). Но вы можете сложить числа, стоящие под одним корнем, например, √(2 + 3) = √(5) (квадратный корень из 2 примерно равен 1,414, квадратный корень из 3 примерно равен 1,732, а квадратный корень из 5 примерно равен 2,236).
   • Нельзя складывать корни с одинаковыми подкоренными выражениями, но разными показателями, например, √(64) + 3 √(64) (эта сумма не равна 5 √(64), так как квадратный корень из 64 равен 8, кубический корень из 64 равен 4, 8 + 4 = 12, что гораздо больше, чем корень пятой степени из 64, который примерно равен 2,297).

Часть 2 Упрощение и сложение корней

1. 1 Определите и сгруппируйте подобные корни. Подобные корни – корни, у которых одинаковые показатели и одинаковые подкоренные выражения. Например, рассмотрим выражение:
   2√(3) + 3 √(81) + 2√(50) + √(32) + 6√(3)
   • Во-первых, перепишите выражение так, чтобы корни с одинаковым показателем располагались последовательно.
     2√(3) + 2√(50) + √(32) + 6√(3) + 3 √(81)
   • Затем перепишите выражение так, чтобы корни с одинаковым показателем и с одинаковым подкоренным выражением располагались последовательно.
     2√(50) + √(32) + 2√(3) + 6√(3) + 3 √(81)
2. 2 Упростите корни. Для этого разложите (где возможно) подкоренные выражения на два множителя, один из которых вынесите из-под корня. В этом случае вынесенное число и множитель корня перемножаются.
   • В приведенном выше примере разложите число 50 на 2*25, а число 32 – на 2*16. Из 25 и 16 можно извлечь квадратные корни (соответственно 5 и 4) и вынести 5 и 4 из-под корня, соответственно умножив их на множители 2 и 1. Таким образом, вы получите упрощенное выражение: 10√(2) + 4√(2) + 2√(3) + 6√(3) + 3 √(81)
   • Число 81 можно разложить на множители 3*27, а из числа 27 можно извлечь кубический корень, равный 3. Это число 3 можно вынести из-под корня. Таким образом, вы получите еще более упрощенное выражение: 10√(2) + 4√(2) + 2√(3)+ 6√(3) + 3 3 √(3)
3. 3 Сложите множители подобных корней. В нашем примере есть подобные квадратные корни из 2 (их можно сложить) и подобные квадратные корни из 3 (их тоже можно сложить). У кубического корня из 3 подобных корней нет.
   • 10√(2) + 4√(2) = 14√(2).
   • 2√(3)+ 6√(3) = 8√(3).
   • Окончательное упрощенное выражение: 14√(2) + 8√(3) + 3 3 √(3)

• Не существует общепринятых правил порядка записи корней в выражении. Потому вы можете записывать корни в порядке возрастания их показателей и в порядке возрастания подкоренных выражений.

В математике корни могут быть квадратными, кубическими или иметь любой другой показатель (степень), который пишется с

electriclub.ru

Как складывать и вычитать квадратные корни

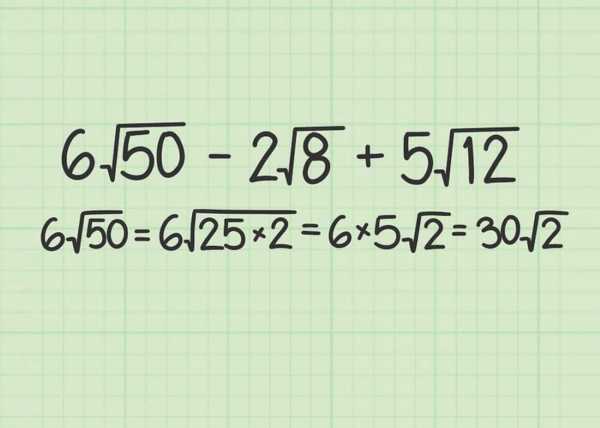
Сейчас в школьной программе происходит, что-то не совсем понятно. Одно радует, что в математике все остается неизменной. Работа с корнями, а именно складывание и вычитание не очень сложное действие. Но у некоторых учеников вызывают определенные трудности.

И в этой статье мы разберем правила, как складывать и вычитать квадратные корни.

Вычитать и складывать квадратные корни можно если срабатывает условие, что у этих корней имеются одинаковые подкоренные выражения. Другими словами, мы можем проводить действия с 2√3 и 4√3, а не с 2√3 и 2√7. Но можно провести действия по упрощению подкоренного выражения, чтобы потом привести их к корням, которые будут иметь одинаковые подкоренные выражения. И только после этого уже начать складывать или вычитать.  

Теория складывания и вычитания квадратных корней

Сам принцип очень простой. И составит из трех действий. Нужно упростить подкоренной выражение. Найти получившиеся одинаковые подкоренные выражения и сложить или вычесть корни.

Как упростить подкоренное выражение

Для этого нужно разложить подкоренное число, что бы состояло из двух множителей. Главное условие. Одно из этих чисел должно быть квадратным числом (пример: 25 или 9). После этого действия мы извлекаем корень из данного квадратного числа. И записываем это число перед нашим корнем, а под корнем у нас остается второй множитель.

Например, 6√50 — 2√8 + 5√12

6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Тут мы раскладываем 50 на два множителя 25 и 2. Потом из 25 мы извлекаем квадратный корень (получаем число 5) и выносим его из под корня. Далее 5 умножаем на 6 и получаем 30√2

2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. В данном примеры мы 8 раскладываем на два числа 4 и 2. Из 4 извлекаем корень и выносим получившееся число за корень и умножаем его на то число которое было уже за корнем.

5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Тут мы, как и раньше число под корнем раскладываем на два числа 4 и 3. Из 4-х извлекаем корень. Получившееся число выносим за корень и перемножаем его на то число которое было за корнем.  

В итоге мы преобразовали уравнение 6√50 — 2√8 + 5√12 в такой вид 30√2 — 4√2 + 10√3

Подчеркиваем корни у которых одинаковы подкоренные выражения

В нашем примере 30√2 — 4√2 + 10√3 мы выделяем 30√2 и 4√2 Так, как у этих чисел одинаковое подкоренное число 2.
Если в Вашем примере несколько одинаковых подкоренных выражений. Подчеркивайте одинаковые из них разными линиями.

Складываем или вычитаем наши корни

Теперь складываем или вычитаем числа которые имеют одинаковые подкоренные выражения. А то, что под корнем мы оставляем неизменным. Смысл в том, чтобы показать сколько всего корней с определенными подкоренными выражениями есть в заданном уравнении.

В нашем примере 30√2 — 4√2 + 10√3 мы от 30 отнимаем 4 и получаем 26√2

Ответ в нашем примере будет такой. 26√2 + 10√3

Sabibon — самое интересное в интернете

sabibon.info