Калькулятор дробей и чисел: Калькулятор рациональных выражений

Калькулятор Дробей — Mathcracker.Com

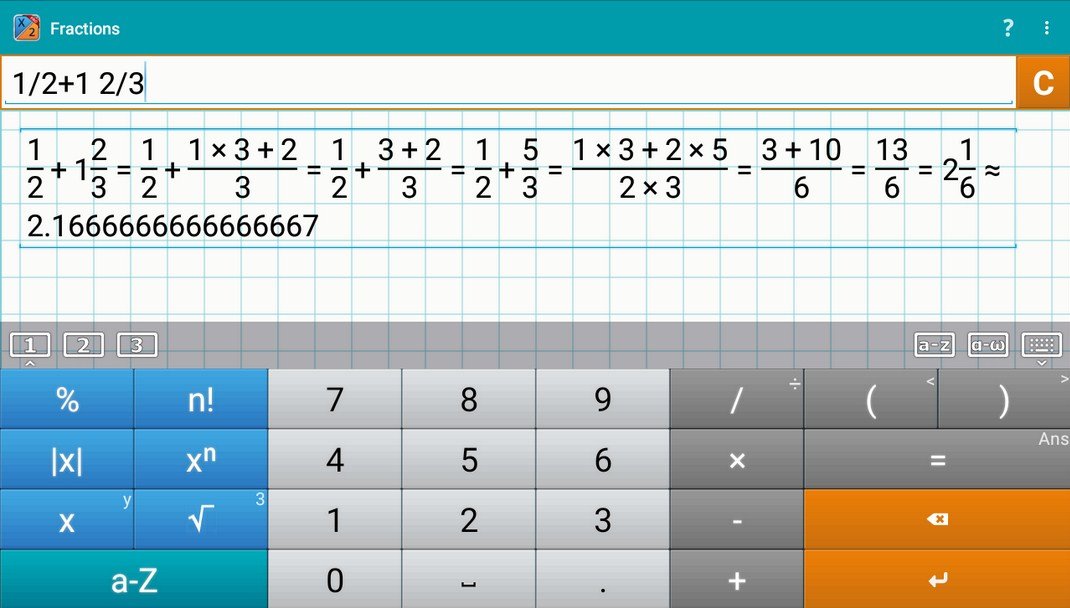
Инструкции: Используйте этот дробный калькулятор для вычисления любой операции с дробями или расчета, который вы предоставите, показывая все шаги. Пожалуйста, введите дробное вычисление, которое вы хотите выполнить, в поле формы ниже.

Подробнее об этом дробном калькуляторе

Этот калькулятор позволит вам сложение дробей , умножение дробей ,

деление дробей , и т. д., и любую допустимую операцию с дробями, показывая все шаги. Вам необходимо предоставить правильное выражение с дробями. Это может быть что-то простое, как «1/2 + 1/3», или что-то более сложное, как ‘(1/3+1/4)(1/5+1/6)’.

Как только вы введете правильное выражение, включающее дробь, вам останется только нажать кнопку «Вычислить», и вам будут представлены все этапы вычислений.

Алгебра дробей включает в себя преобразование дробей, такое как использование общего знаменателя, и использование основных арифметических правил. В целом, процесс вычисления может быть трудоемким, хотя его можно выполнять систематически, без особых проблем.

Как складывать дроби?

Сложение дробей — один из самых важных и основных навыков, который вы будете использовать при вычислении операций с дробями. Обычно нужно начинать с нахождения общего знаменателя, но часто для сложения дробей используется следующая формула:

\[\displaystyle \frac{a}{b} + \frac{c}{d} = \displaystyle \frac{ad + cb}{bd} \]

Каковы этапы сложения дробей?

• Шаг 1: Определите числитель и знаменатель первой и второй дроби
• Шаг 2: Предположим, что a и b — числитель и знаменатель первой дроби, а c и d — числитель и знаменатель второй дроби
• Шаг 3: Используйте формулу сложения: Полученная дробь имеет числитель ad + cb, а знаменатель — bd

Вычитание дробей — это просто производная от суммы дробей: Чтобы вычесть две дроби, нужно просто умножить вторую на -1, а затем прибавить ее к первой

.

Как умножить дроби?

Вторым краеугольным камнем для проведения общих дробных вычислений является умножение дробей. В этом случае нет необходимости находить общий знаменатель, вы просто перемножаете числители и знаменатели вместе:

\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]

Каковы этапы умножения дробей?

• Шаг 1: Определите числитель и знаменатель первой и второй дроби
• Шаг 2: Предположим, что a и b — числитель и знаменатель первой дроби, а c и d — числитель и знаменатель второй дроби
• Шаг 3: Используйте формулу сложения: Полученная дробь имеет числитель ad + cb, а знаменатель — bd

Подобно тому, как это произошло со сложением и вычитанием, деление дробей просто вытекает из умножения дробей: Чтобы разделить две дроби, нужно просто умножить первую на обратная дробь

второй (обратная дробь получается путем замены числителя на знаменатель в дроби).

Зачем нужно вычислять дроби?

Дроби — один из краеугольных камней алгебры и любого общего курса алгебраическое выражение для вычисления . Дроби являются простыми операндами, но их можно объединить в более сложные понятия, используя такие операции, как сумма, умножение и т.д., а затем, используя функции, мы можем построить еще более сложные выражения.

Центр всего алгебраического калькулятора начинается с мощности основных чисел дробей.

Пример: вычисление суммы дробей

Вычислите следующее: \(\frac{1}{3} + \frac{5}{4} — \frac{5}{6}\)

Решение:

Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\).

Получается следующий расчет:

\( \displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\)

Amplifying in order to get the common denominator 12

\( = \,\,\)

\(\displaystyle \frac{1}{3}\cdot\frac{4}{4}+\frac{5}{4}\cdot\frac{3}{3}-\frac{5}{6}\cdot\frac{2}{2}\)

Finding a common denominator: 12

\( = \,\,\)

\(\displaystyle \frac{1\cdot 4+5\cdot 3-5\cdot 2}{12}\)

Expanding each term: \(4+5 \times 3-5 \times 2 = 4+15-10\)

\( = \,\,\)

\(\displaystyle \frac{4+15-10}{12}\)

Adding each term

\( = \,\,\)

\(\displaystyle \frac{9}{12}\)

We can factor out 3 for both the numerator and denominator.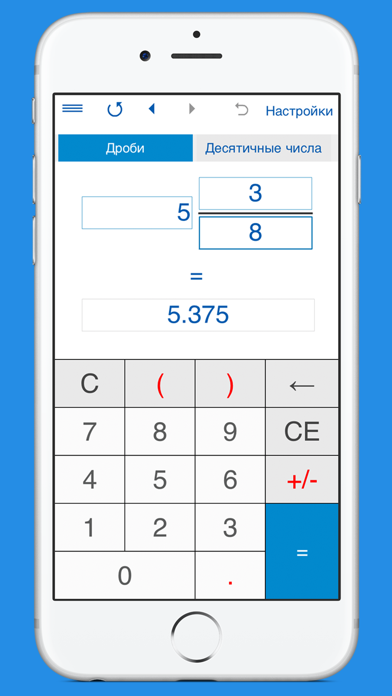

\( = \,\,\)

\(\displaystyle \frac{3\cdot 3}{3\cdot 4}\)

Now we cancel 3 out from the numerator and denominator.

\( = \,\,\)

\(\displaystyle \frac{3}{4}\)

чем завершается расчет.

Пример: еще одно вычисление дробей

Рассчитайте \( \left(\frac{2}{3} \times \frac{6}{5} \right)+ \frac{2}{5} \).

Решение:

Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \left(\frac{2}{3}\cdot\frac{6}{5}\right)+\frac{2}{5}\).

Получается следующий расчет:

\( \displaystyle \left(\frac{2}{3} \times \frac{6}{5} \right)+ \frac{2}{5} \)

We can multiply the terms in the top and bottom as in \(\displaystyle\frac{ 2}{ 3} \times \frac{ 6}{ 5}= \frac{ 2 \times 6}{ 3 \times 5} \)

\( = \,\,\)

\(\displaystyle \frac{2\cdot 6}{3\cdot 5}+\frac{2}{5}\)

We can factor out the term \(\displaystyle 3\) in the numerator and denominator in \(\displaystyle \frac{ 2 \times 6}{ 3 \times 5}\)

\( = \,\,\)

\(\displaystyle \frac{2\cdot 2}{5}+\frac{2}{5}\)

After canceling out the common factors

\( = \,\,\)

\(\displaystyle \frac{4}{5}+\frac{2}{5}\)

We use the common denominator: 5

\( = \,\,\)

\(\displaystyle \frac{4+2}{5}\)

Adding each term

\( = \,\,\)

\(\displaystyle \frac{6}{5}\)

чем завершается расчет.

Другие полезные дробные калькуляторы

Вычисления с дробями имеют решающее значение в алгебре. Другие полезные операции включают упрощение дроби путем снижения до самых низких условий. Кроме того, вы можете перевести дробь в проценты или же дробь до десятичной так как между ними существует интимная связь.

Также вас может заинтересовать калькулятор смешанных дробей в зависимости от условий обучения.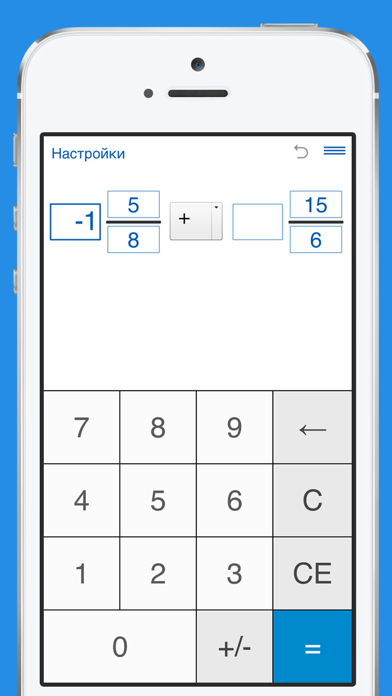 В более элементарных условиях смешанные числа рассматриваются как важные объекты, в то время как в более продвинутых условиях смешанные числа просто представляются в их дробной нотации.

Сравнение обыкновенных дробей. Онлайн калькулятор

• Сравнение дробей с одинаковыми знаменателями
• Сравнение дробей с одинаковыми числителями
• Сравнение дробей с разными знаменателями и числителями
• Сравнение дроби с натуральным числом
• Равенство дробей
• Онлайн калькулятор сравнения дробей

Сравнить две дроби — значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.

Сравнение дробей с одинаковыми знаменателями

Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.

Пример. Дробь    больше чем дробь  ,  потому что доли в обеих дробях одинаковы, но в первой дроби их больше, чем во второй.

Если изобразим единицу отрезком и разделим его на 8 долей, то легко увидеть, что дробь    больше  :

Сравнение дробей с одинаковыми числителями

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.

Пример. Дробь    больше чем дробь  ,  потому что число долей в обеих дробях одинаково, но в первой дроби доли крупнее, чем во второй.

Изобразим две единицы в виде кругов, один разделим на  4  доли, второй на  6  долей. Теперь можно увидеть, что дробь    больше  :

Сравнение дробей с разными знаменателями и числителями

Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Пример. Сравните дроби:    и  .

Решение: приводим данные дроби к общему знаменателю:

Теперь сравниваем их по правилу сравнения дробей, у которых одинаковые знаменатели. Так как  , значит  .

Приведём ещё один способ сравнения дробей с разными знаменателями и числителями. Рассмотрим сначала числовой пример.

Пример. Сравним дроби    и  .

Решение: приводим данные дроби к общему знаменателю:

Решая данный пример можно заметить, что, после приведения дробей к общему знаменателю, задача сравнения свелась фактически к сравнению произведений

2 · 7    и    4 · 3.

Так как  2 · 7 = 14,  а  4 · 3 = 12,  то

2 · 7 > 4 · 3.

Значит,  .

Теперь решим эту же задачу в общем виде, используя буквенную запись.

Пример. Пусть даны дроби    и  ,  где  a  и  c  — нуль или натуральные числа,  b  и  d  — натуральные числа. Приведём дроби к общему знаменателю:

Следовательно:

1. если  a · d > c · b,  то   
2. если  a · d < c · b,  то   
3. если  a · d = c · b,  то   

Таким образом мы получили следующее правило сравнения обыкновенных дробей:

Чтобы сравнить две обыкновенные дроби, можно числитель одной дроби умножить на знаменатель другой и полученные произведения сравнить.

Это правило называется перекрёстным правилом сравнения дробей.

Сравнение дроби с натуральным числом

Любая правильная дробь меньше любого натурального числа.

Пример.

Сравнение неправильной дроби с натуральным числом сводится к сравнению двух дробей.

Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби со знаменателем  1,  затем их можно сравнить одним из двух способов: используя перекрёстное правило, либо привести дроби к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Пример. Сравните дробь    с числом  5.

Решение: представим число  5  в виде дроби со знаменателем  1:

Приводим дроби к общему знаменателю:

Сравниваем числители, так как  11 < 15,  то  ,  значит,  .

Равенство дробей

Две обыкновенные дроби считаются равными, если равны их числители и знаменатели или если они выражают одну и ту же часть единицы.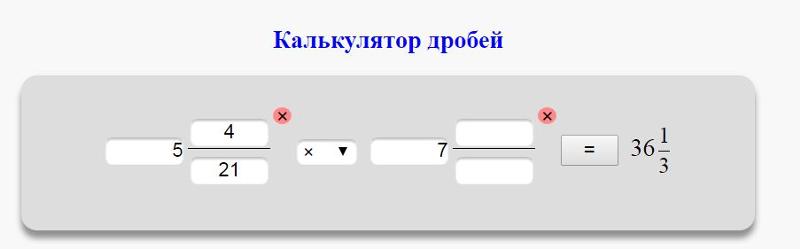

Пример.

Онлайн калькулятор сравнения дробей

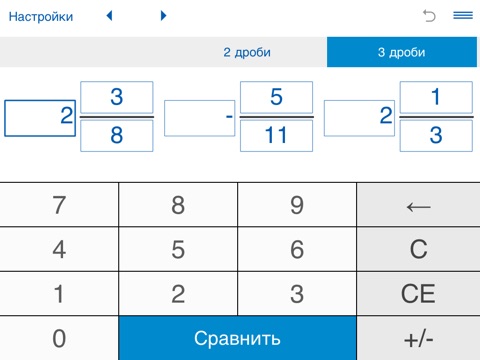
Данный калькулятор поможет вам сравнить обыкновенные дроби. Просто введите две дроби и нажмите кнопку Сравнить.

Калькулятор смешанных чисел

Этот калькулятор выполняет основные и расширенные операции со смешанными числами, дробями, целыми и десятичными дробями. Смешанные числа также называют смешанными дробями. Смешанное число — это целое число и правильная дробь, то есть одна и три четверти. Калькулятор оценивает выражение или решает уравнение с пошаговой информацией о ходе вычислений. Решите задачи с двумя и более дробями смешанных чисел в одном выражении.

Что такое смешанное число?

Смешанное число — это целое число и дробь acb, значение которого равно сумме этого целого числа и дроби. Например, мы пишем две и четыре пятых как 254​. Его значение: 254​=2+54​=510​+54​=514​. Смешанное число является исключением: отсутствующий операнд между целым числом и дробью является не умножением, а сложением: 254​​=2⋅ 54​. Отрицательное смешанное число — знак минус также применяется к дробному числу −254​=−(254​)=−(2+54​)=−514​. Смешанное число иногда называют смешанной дробью. Обычно смешанное число содержит натуральное число и правильную дробь, а его значением является неправильная дробь, то есть такая, у которой числитель больше знаменателя.

Как представить смешанное число?

Мы можем представить смешанные числа на примере тортов. У нас есть три лепешки, и мы разделили каждую на пять частей. Таким образом, мы получили 3 * 5 = 15 кусочков торта. Цельный, когда мы едим, остается 14 кусочков, что составляет 254 торта. Когда мы съедаем два куска, остается 253 торта.

Примеры:

• сумма двух смешанных чисел: 1 3/4 + 2 3/8
• сложение трех смешанных чисел: 1 3/8 + 6 11/13 + 5 7/8
• сложение двух смешанных чисел числа: 2 1/2 + 4 2/3
• вычитание двух смешанных чисел: 7 1/2 — 5 3/4
• умножение смешанных чисел: 3 3/4 * 2 2/5
• сравнение смешанных чисел: 3 1/4 2 1/3
• замена неправильного дробь в смешанном числе: 9/4
• Что такое 3/4 как смешанное число: 3/4
• вычитание смешанного числа и дроби: 1 3/5 — 5/6
• суммирование смешанного числа и неправильной дроби: 1 3/5 + 11/5

Смешанное число в текстовых задачах:

• Какое 5
  Какое смешанное число эквивалентно 2,68? A:2 и 6 восьмых B:2 и 68 десятых C:2 и 6 больше 68
• Mixed2improper
  Запишите смешанное число в виде неправильной дроби: 166 2/3
• Расчет Петра
  Петр написал следующее: 7 1/4 — 3 3/4 = 4 2/4 = 4 1/2 . Верен ли расчет Петра? Используя слова (математический словарь) и числа, чтобы объяснить, почему он прав или неправ.
• Смешанные числа в неправильные
  Измените данные смешанные числа на неправильные дроби: пять и четыре на девять (5 4/9)
• Пироги
  Миссис Моника печет пироги. Она всегда разрезает каждый пирог на восемь частей. На прилавке осталось 13 ломтиков. Запишите количество пирожков на прилавке в виде смешанного числа и в виде неправильной дроби.
• Преобразовать 4
  Преобразовать 2 7/10 в неправильную дробь.
• Преобразовать 5
  Преобразовать в смешанное число и упростить: 83/6
• Миссис Джонс
  Миссис Джонс печет пироги. Она всегда разрезает каждый пирог на восемь частей. На прилавке осталось 13 ломтиков. Запишите количество пирогов на прилавке в виде смешанного числа.
• Zailene 2
  Zailene имеет 8 2/3 стакана муки. Она использовала 5 1/2 стакана муки. Сколько чашек муки осталось ей?
• Вычесть смешанный
  Найди разницу. Пять и две трети минус два с половиной равно какому числу? A. три и одна шестая B. три и две трети C. три с половиной D. три и пять шестых
• Сколько 3
  Насколько 1⅝ больше, чем 4⅚?

другие математические задачи »

Калькулятор дробей — Вычисление дробей

Вычисление дробей — это специальный калькулятор для умножения, деления, сложения и вычитания двух или более дробей и целых чисел. Он может обрабатывать несколько дробей и целых чисел одновременно. Затем он отображает пошаговые решения любой операции, которую он обработал. Иногда мало кто назовет его решателем дробей, в то время как другие могут сказать, что это калькулятор смешанных чисел или калькулятор смешанных дробей. Это онлайн-калькулятор с кнопкой дроби. На данный момент он может вычислять до десяти дробей и смешанных чисел. Это полезно для всех учащихся всех классов. Его можно использовать в качестве справочника для всех учителей математики и даже для тех специалистов, которые часто используют дроби на работе или дома.

Упрощение

Backspace

Целые числа

Числители

Знаменатели

---

Как использовать?

Этот калькулятор был разработан для удобства использования.

• Сложение двух дробей

1. Нажмите любую цифру из кнопок числителя.
2. Нажмите любую цифру из кнопок знаменателя.
3. Нажмите кнопку добавления (+) .
4. Нажмите любую цифру из кнопок числителя для второй дроби.
5. Нажмите любую цифру из кнопок знаменателя для второй дроби.
6. Нажмите кнопку, равную (=) , чтобы рассчитать ответ. Ответ и решение будут отображаться выше.

Добавление трех или более дробей

1. Повторите шаги, описанные выше, за исключением последнего шага.
2. Нажмите кнопку добавления (+) .
3. Нажмите любую цифру из кнопок числителя для третьей дроби.
4. Нажмите любую цифру из кнопок знаменателя для третьей дроби.
5. Нажмите кнопку равно (=) , чтобы вычислить ответ, или нажмите кнопку добавления (+) , чтобы добавить другие дроби.
6. Тот же процесс будет использован для четвертой, пятой или любого количества фракций. Просто нажмите кнопку равно (=) для вычисления.

Вычитание двух, трех и более дробей

• Следуйте инструкциям по сложению дробей, но вместо нажатия кнопки добавления (+) нажмите кнопку вычитания (-) .

Умножение и деление двух, трех и более дробей

• Следуйте инструкциям по сложению дробей, но вместо нажатия кнопки добавления (+) нажмите кнопку умножения (x) для умножения и деления (÷) кнопку для разделение.

Сложение, вычитание, умножение и деление смешанных чисел

Важно помнить, что при работе со смешанными числами при использовании этого калькулятора никогда не забывайте вводить целые числа. Кнопки целых чисел в калькуляторе больше, чем кнопки числителя и знаменателя.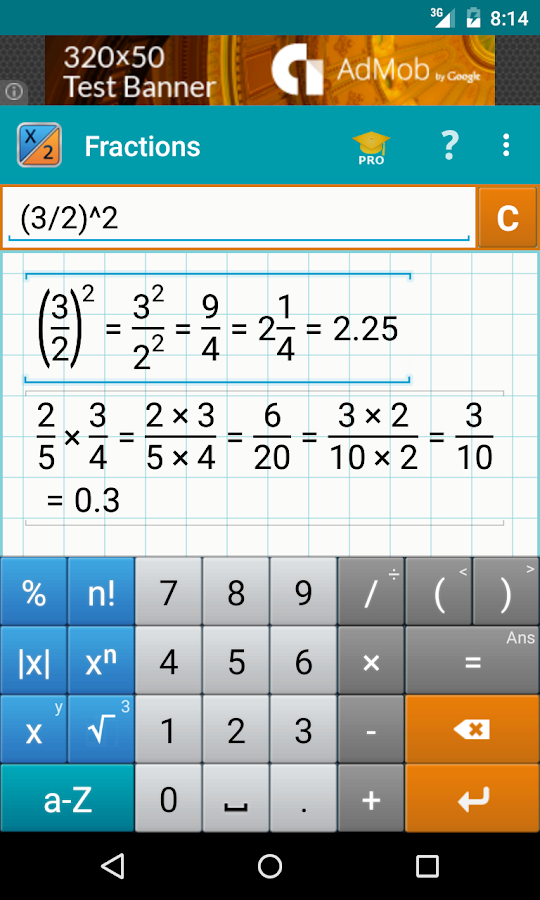 Вам нужно только сначала нажать кнопку целого числа, а затем дробь, после чего вы можете перейти к любой операции, которую хотите.

Операции с дробями, целыми числами и смешанными числами

1. Нажмите кнопку целого числа, если ваша дробь состоит из целого числа, или вы можете напрямую нажать кнопку числителя, если вам не нужно целое число. Вы не можете нажать кнопку знаменателя, если вы не нажали целое число или кнопку знаменателя. Это означает, что вам нужно сначала нажать кнопку целого числа или числителя. После нажатия кнопки числителя вы больше не можете нажимать кнопку целого числа. Вы можете нажать кнопку целого числа еще раз только в том случае, если вы удалите числитель, нажав кнопку возврата. Нули не должны быть нажаты первыми. Нули будут нажаты после нажатия ненулевых чисел.
2. Нажмите кнопку знаменателя для вашего знаменателя. После нажатия вы не можете снова нажать кнопку целого числа или числителя. Вы можете нажать кнопку числителя только в том случае, если вы удалите знаменатель, нажав кнопку возврата.
3. Выберите любую операцию.
4. Нажмите кнопку Равно , если вы закончили с дробью. Решение будет отображаться выше.
5. Нажмите Backspace , если вы хотите удалить по одному номеру за раз.
6. Нажмите AC кнопка для очистки уравнения дроби.
7. На данный момент этот калькулятор ограничен только 10 дробями.

---

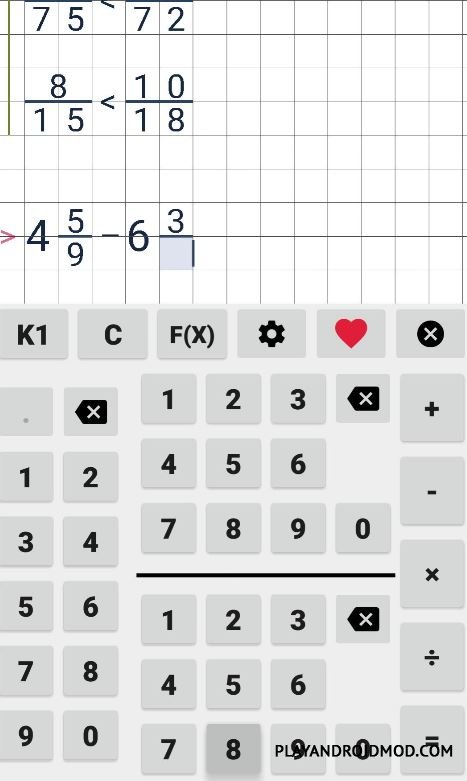
Расчет дробей на мобильных телефонах Android

Выпущен наш калькулятор дробей для мобильных телефонов Android. Он может обрабатывать базовые и сложные операции с дробями и может отображать решение как методом перекрестного умножения, так и методом LCD (наименьший общий знаменатель). Вы можете получить его из магазина Google Play.

Как был выполнен расчет?

Иногда возникают сомнения в том, как выполняются вычисления при использовании нескольких операций. Используя нотацию MDAS, умножение и деление имеют такой же приоритет, но выше, чем сложение и вычитание. Сложение и вычитание имеют одинаковый приоритет. Сначала обрабатывается более высокий приоритет. Это всегда было правилом, и оно соблюдалось повсеместно. При одинаковом приоритете операция выполняется слева направо.

---

Калькулятор дроби целых чисел

Fraction Calc также является калькулятором целочисленных дробей, потому что он может работать со многими целыми числами. Работа с целыми числами означает, что вам придется больше учиться и делать дополнительные шаги, преобразовывая целые числа в формат, подходящий для математических операций. Выполнение математических операций с целыми числами означает, что вам нужно выполнить дополнительные действия, чтобы получить правильный ответ. Это означает дополнительную энергию и нагрузку для людей, которые оказались в ситуации, когда им нужно решать целые числа и дроби. Вот почему некоторые люди ищут калькулятор дробей и целых чисел не только с целью предоставления простых решений сложных задач, но и для экономии времени и энергии. Экономия времени и энергии на определенной задаче означает, что вы получаете дополнительные ресурсы для выполнения еще более важной задачи, которая была бы очень полезной.

---

3 Калькулятор дробей

В большинстве случаев в любой математической арифметике используются только две дроби. Очень редко в какой-либо операции участвуют 3 фракции. Но если это ваш случай, то вам очень повезло, что вы нашли этот инструмент. Вы можете легко использовать этот инструмент в качестве калькулятора 3-х дробей, потому что он может абсолютно решить эту проблему. Это основная цель этого инструмента. Некоторые люди никогда не слышали об этом инструменте, поэтому они специально искали калькулятор с тремя дробями. Но теперь, когда его инструмент создан, я думаю, у них больше нет времени беспокоиться.

---

Калькулятор кратных дробей

Большинство созданных калькуляторов имеют ограниченные возможности до такой степени, что могут вычислять только две дроби за раз. Но Fraction Calc может даже больше. Он может решить до 10 целых чисел или дробей вместе взятых. Вот почему многие называют его калькулятором кратных дробей. Это очень специализированный калькулятор с целыми числами. С комбинацией целого числа и дроби трудно иметь дело, но с этим калькулятором кратных дробей вычисления становятся проще. Сложение смешанных чисел, преобразование дробей в целые числа, умножение дробей на целые числа, вычитание смешанных чисел и умножение смешанных дробей — вот некоторые из процессов, которые может выполнять этот калькулятор.

---

Преимущества и недостатки использования калькулятора дробей.

• Преимущества:

1. Прост в использовании.
2. Экономит больше времени и энергии.
3. Нет необходимости в ручном вычислении.
4. Вычисленный результат точен и точен.

Недостатки:

1. Это может затруднить вычисление дробей.
2. Вы будете очень зависеть от него в будущем.
3. Вы можете забыть правила вычисления.

---

Правила работы с дробями

• Сложение и вычитание дробей

Сложение и вычитание дробей выполняются по одним и тем же правилам. Они должны иметь одинаковые знаменатели для выполнения выбранной операции. Вы можете сложить или вычесть две дроби, если у них один и тот же знаменатель, если нет; вы должны создать общий знаменатель, прежде чем складывать или вычитать их.

Подобные дроби — это дроби, имеющие одинаковые знаменатели. Чтобы сложить дроби с одинаковым знаменателем, добавьте его числитель. Например, 2/5 + 1/5 = 3/5.

Дроби, имеющие разные знаменатели, не похожи на дроби. Чтобы сложить разные дроби, нужно привести их к общему знаменателю. Самый простой способ сделать это — использовать метод бабочки. Чтобы выполнить метод бабочки, выполните следующие действия.

1. Умножьте числитель первой дроби на знаменатель второй дроби. Результатом будет первый числитель дроби.
2. Умножьте знаменатель первой дроби на знаменатель второй дроби. Результатом будет новый знаменатель первой дроби.
3. Умножьте числитель второй дроби на знаменатель первой дроби. Результатом будет новый числитель второй дроби.
4. Умножьте знаменатель второй дроби на знаменатель первой дроби. Результат теперь является новым знаменателем второй дроби.

Например: 2/3 + 3/5.

1. 2 х 5 = 10.
2. 3 х 5 = 15.
3. 3 х 3 = 9.
4. 5 х 3 = 15.

Новая фракция: 10/15 и 9/15.
15/10 + 15/9 = 15/19.
Новая дробь 19/15.

Чтобы вычесть дроби с одинаковым знаменателем, просто вычтите числитель второй дроби из числителя первой дроби. Пример: 4/6 – 3/6 = 1/6.

Для дробей с разными знаменателями приведите их к одному знаменателю, используя метод бабочки, а затем выполните вычитание после того, как у них будет одинаковый знаменатель.

Умножение и деление дробей

Правило умножения двух дробей простое. Умножьте числитель первой дроби на числитель второй дроби и умножьте знаменатель первой дроби на знаменатель второй дроби. Пример: 2/3 х 1/5 = 2/15.

Чтобы разделить две дроби, вы должны сначала инвертировать вторую дробь, а затем начать умножать две дроби. Пример: 2/3 разделить на 1/5 = 2/3 x 5/1 = 10/3.

Как заменить неправильную дробь смешанным числом

Когда вы сокращаете неправильную дробь до наименьшего члена, вам нужно преобразовать ее в смешанное число. Это делается делением числителя на знаменатель. Частное будет целым числом. Остаток будет новым числителем, а знаменатель останется прежним.

Как превратить смешанное число в неправильную дробь

При делении или умножении смешанных чисел вам нужно, чтобы оно превратилось в неправильную дробь. Это делается путем умножения целого числа на знаменатель, а затем добавления текущего числителя. Результатом будет новый числитель, а знаменатель останется прежним.

Сравнение дробей

Для дробей с одинаковыми знаменателями дробь с наибольшим числителем является большей, чем дробь с меньшим числителем.
Для дробей с одинаковыми числителями дробь с наибольшим знаменателем меньше дроби с меньшим знаменателем.

Упрощение дробей

Из темы выше мы уже знаем, что есть равнозначные дроби-дроби, одинаковые по значению, даже если у них разные числители и знаменатели. Упрощение дроби означает использование наименьшего числителя и знаменателя, но одного и того же значения. Дробь имеет простейшую форму, когда нет общего множителя для числителя и знаменателя. Например, вместо использования 7/14 мы можем использовать ½, что является самой простой формой.

Наибольший общий делитель

Наибольший общий делитель — это наибольшее число, используемое для деления числителя и знаменателя для получения простейшей формы дроби. Например, для дроби 12/30 наибольшее число, на которое можно разделить как числитель, так и знаменатель, равно 6. Разделив его на 6, вы получите его простейшую форму — 2/5.

---

Факты о дробях

Дроби являются частями целого. Например, один торт на пятерых детей. Итак, торт делится на пять частей. Каждый ребенок получит одну часть торта. Дробь будет 1/5. Каждый ребенок получит 1/5 торта.

Дробь состоит из двух частей. Верхняя половина называется числителем. Нижняя половина называется знаменателем. Числитель — это часть целого, где она используется или с которой в настоящее время имеют дело.

Существуют три типа дробей: правильная дробь, неправильная дробь и смешанные числа.

Правильная дробь — это дробь, числитель которой всегда меньше знаменателя.

Неправильная дробь – это дробь, числитель которой больше или равен знаменателю.

Смешанное число представляет собой целое число плюс дробь.

Равные дроби — это дроби, которые имеют разные числители и знаменатели, но имеют одинаковое значение, например 1/2, 2/4, 7/14, 8/16, 10/20, 20/40 и 50/100.

---

Как был создан расчет дробей?

Когда я был студентом, у меня был предмет по математике. Одна из тем была о дроби. Хотя эта тема сложна, меня очень удивило, почему трудно определить, правильное решение или нет. Вы должны просмотреть его несколько раз, чтобы убедиться, что ваше решение является правильным. Это произошло не только у меня. Я узнал, что большинство студентов испытывали то же самое.