Калькулятор с иксами: Решение уравнений бесплатно · Калькулятор Онлайн

Калькулятор Решения Для X — Mathcracker.Com

Решатели Алгебра

Инструкции: Используйте этот пошаговый калькулятор, чтобы найти x из предложенного вами линейного уравнения. Введите допустимое линейное уравнение в поле ниже.

Подробнее об этом калькуляторе решения для x

Традиционно вам нужно решать уравнения, и наиболее распространенная настройка — это решение уравнений, когда есть только одна переменная.

Но также может быть случай, когда вы хотите решить уравнение, когда присутствует более одной переменной. В этом случае вы говорите, что решаете для этой переменной, а не для любой другой присутствующей переменной.

Случай с линейное уравнение , с двумя переменными \(x\) и \(y\) — это один из самых простых случаев, когда вы можете решить для одной из переменных, в данном случае \(x\).

Как использовать этот решатель x

Это очень просто:

Шаг 1: Первое, что вам нужно сделать, это ввести линейное уравнение, например «2x — 3y = 3» или что-то вроде «x — 2y = 4».

Шаг 2: Если предоставлено действительное линейное уравнение, калькулятор попытается найти значение x и, если возможно, решит для x, показывая все шаги.

Шаг 3: Конечным результатом является выражение x как функции y, если это возможно, или вывод об отсутствии решения для x.

Как вы решаете для x?

Идея проста: вам нужно манипулировать уравнением, используя алгебраически допустимые шаги, чтобы получить только \(x\) на одной стороне уравнения. В общем случае это не всегда просто, но это для линейных уравнений.

Например, у вас может быть уравнение \(2x + 3y = 2\), вам нужно поместить \(x\) целиком в левую часть, поэтому вы вычитаете \(3y\) из обеих частей уравнения, что дает эффект отмены \(3y\) в левой части и включения \(-3y\) в правой части уравнения.

Вот что происходит, когда мы говорим «мы передаем \(3y\) на другую сторону со знаком минус».

Этот метод «передачи термина на другую сторону с измененным знаком» — это способ перемещать переменные, чтобы найти желаемую переменную.

Как решить для x с шагами

Чтобы получить шаги для решения \(y\) для заданного линейного уравнения, вам просто нужно ввести уравнение в соответствующем поле. Все, что требуется, это чтобы предоставленное линейное уравнение было верным.

Вместо этого вас может заинтересовать \(y\), и в этом случае вы можете использовать это решить для y калькулятор если вы хотите найти \(y\) вместо \(x\), если это то, что вам нужно.

Пример: Решение для x:

Найдите \(x\) для данного уравнения \(2x + 3y = 2\).

Отвечать:

Нам было предложено следующее уравнение:

\[\displaystyle 2x+4y=4\]

Помещая \(x\) в левую часть и \(y\) и константу в правую часть, мы получаем

\[\displaystyle 2x = -4y +4\]

Теперь, находя \(x\), получаем следующее

\[\displaystyle x=-\frac{4}{2}y+\frac{4}{2}\]

и упрощая все термины, которые нуждаются в упрощении, окончательно получаем следующее

\[\displaystyle x=-2y+2\]

решить для х калькулятор Решение For x Calculator Линейные Уравнения Решите Линейные Уравнения Решение для калькулятора переменных

Онлайн калькулятор: Кубическое уравнение

УчебаМатематикаАлгебра

Решение кубического уравнения по формуле Виета. Создан по запросу пользователя.

Сегодня выполняем запрос пользователя Решение кубического уравнения.
Канонический вид кубического уравнения:

Решать кубическое уравнение мы будем по формуле Виета.
Формула Виета — способ решения кубического уравнения вида

Соответственно, чтобы привести к этому виду оригинальное уравнение первым шагом все введенные коэффициенты делятся на коэффициент а:

Калькулятор ниже, а описание формулы Виета — под ним

Кубическое уравнение

коэффициент а

коэффициент b

коэффициент c

коэффициент d

Детали

Точность вычисления

Знаков после запятой: 2

Кстати сказать, на других сайтах почему-то для решения кубических уравнений используют формулу Кардано, однако я согласен с Википедией в том, что формула Виета более удобна для практического применения. Так что почему везде формула Кардано — непонятно, разве что лень людям Гиперболические функции и Обратные гиперболические функции реализовывать. Ну мне не лень было.

Итак, формула Виета (из Википедии)

Обратите внимание, что по представлению формулы Виета а — второй коэффициент, а коэффициент перед x³ всегда считается равным 1. Калькулятор позволяет ввести а как коэффициент перед х³, но сразу же на него и делит уравнение, чтобы получить 1

Вычисляем:

Вычисляем:

Если S > 0, то вычисляем:

и имеем три действительных корня:

Если S < 0, то заменяем тригонометрические функции гиперболическими. Здесь возможны три случая в зависимости от Q

Q > 0:

(действительный корень)

(пара комплексных корней)

Q < 0:

(действительный корень)

(пара комплексных корней)

Q = 0:

(действительный корень)

(пара комплексных корней)

Если S = 0, то уравнение вырождено и имеет меньше 3 различных решений (второй корень кратности 2):

По этим формулам калькулятор и работает. Решает вроде правильно, хотя решения с мнимой частью не проверял. Если что, пишите.

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Уравнение прямой по двум точкам
• • Решение квадратного уравнения
• • Уравнения прямой, проходящей через две точки в трехмерном пространстве
• • Решение уравнения 4-й степени
• • Решение системы двух уравнений первой степени с двумя неизвестными
• • Раздел: Алгебра ( 46 калькуляторов )

 #математика #уравнение Алгебра кубическое уравнение Математика уравнение формула Виета

 PLANETCALC, Кубическое уравнение

Timur2022-06-28 08:32:23

Калькулятор решения для x — MathCracker.com

Решатели Алгебра

Инструкции: Используйте этот пошаговый калькулятор, чтобы найти x из предложенного вами линейного уравнения. Пожалуйста, введите допустимое линейное уравнение в поле предоставлено ниже.

Подробнее об этом калькуляторе решения для x

Традиционно вам приходится решать уравнения, и чаще всего приходится решать уравнения, когда есть только одна переменная.

Но также может быть случай, когда вы хотите решить уравнение, когда присутствует более одной переменной. В таком случае, вы говорите, что решаете для этой переменной, в отличие от решения для любой другой присутствующей переменной.

Случай линейного уравнения с двумя переменными \(x\) и \(y\) является одним из самые простые случаи, которые вы можете иметь, в которых вы можете найти одну из переменных, \(x\) в этом случае.

Как использовать этот решатель x

Это очень просто:

Шаг 1: Первое, что вам нужно сделать, это ввести линейное уравнение, например, «2x — 3y = 3» или что-то вроде «x — 2y = 4»

Шаг 2: Одно верное линейное уравнение, калькулятор попытается найти значение x и, если возможно, решит для x, показывая все шаги

Шаг 3: Окончательный результат: выражение x как функции y, если это возможно, или прийти к выводу, что для x нет решения

Как вы решаете для X?

Идея проста: вам нужно манипулировать уравнением, используя алгебраически корректные шаги, чтобы получить \(x\) только с одной стороны уравнения. В общем случае это не всегда просто, но это для линейных уравнений.

Например, у вас может быть уравнение \(2x + 3y = 2\), вам нужно, чтобы \(x\) помещался один в левой части, поэтому вы вычитаете \(3y\) из обеих частей уравнения, что приводит к отмене \(3y\) с левой стороны и появлению \(-3y\) с правой стороны уравнения.

Вот что происходит, когда мы говорим «переходим \(3y\) на другую сторону со знаком минус».

Этот метод «передачи термина на другую сторону с измененным знаком» представляет собой способ перемещения переменных, чтобы решить для искомой переменной.

Как решить для x с помощью шагов

Чтобы получить шаги для решения для \(y\) для данного линейного уравнения, вам просто нужно ввести уравнение в соответствующем поле. Все это требуется, чтобы представленное линейное уравнение было действительным.

Вместо этого вас может заинтересовать \(y\), и в этом случае вы можете использовать это решение для калькулятора y если вы хотите найти \(y\) вместо \(x\), если это то, что вам нужно.

Пример: Решение для x:

Найдите \(x\) для данного уравнения \(2x + 3y = 2\).

Ответ:

Мы получили следующее уравнение:

\[\displaystyle 2x+4y=4\]

Положив \(x\) в левую часть, а \(y\) и константу в правую, получим

\[\displaystyle 2x = -4y +4\]

Теперь, решая \(x\), получаем следующее

\[\displaystyle x=-\frac{4}{2}y+\frac{4}{2}\]

и упрощая все термины, которые нуждаются в упрощении, окончательно получаем следующее

\[\displaystyle х=-2у+2\]

Решить для x калькулятор Решение For x Calculator Линейные уравнения Решите линейные уравнения Решение для калькулятора переменных

Математика для iPad в App Store

Описание

Бесплатный калькулятор №1 для iPad, iPhone и Apple Watch с 200 000 загрузок.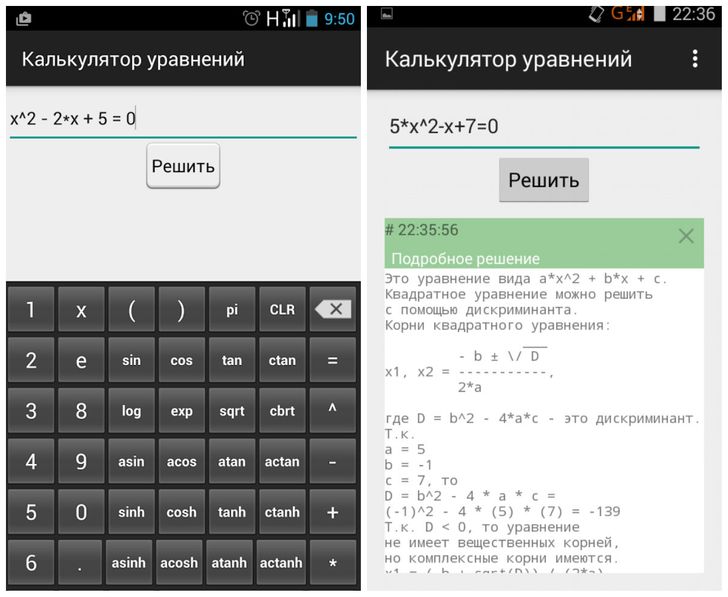

Калькулятор — бесплатное приложение с расширенными функциями, которое повышает вашу продуктивность!
Загрузите сейчас и присоединяйтесь к клубу пользователей, впечатленных продуктом!

ПОЧЕМУ ВАМ ПОНРАВИТСЯ КАЛЬКУЛЯТОР
• Простой и простой в использовании калькулятор
• История расчетов: сохранение, копирование и обмен
• Редактировать уравнение
• Последний расчет в памяти
• Темный режим
• Поддержка Apple Watch
• Перетаскивание
• Разделенный вид

РЕДАКТИРОВАНИЕ УРАВНЕНИЯ ВО ВРЕМЯ РАСЧЕТА
Вы можете редактировать числа в любое время в процессе расчета.

ТЕМНЫЙ РЕЖИМ
Переключитесь в темный режим и наслаждайтесь дизайном! Темный режим защищает глаза от ярких цветов, экономит заряд батареи и помогает лучше сфокусироваться.

ПОДЕЛИТЕСЬ СВОИМИ РАСЧЕТАМИ
Получили отличный результат при расчете? Экономьте время и отправляйте сообщения своим контактам быстро и просто, поделившись с калькулятором.

МЫ ЖДЕМ ОБРАТНОЙ СВЯЗИ
Мы всегда ценим ваши отзывы. Продолжайте делиться своим опытом, ошибками и идеями по адресу [email protected]

Нравится калькулятор и хотите больше возможностей? Пожалуйста, подарите нам немного любви, поставив 5-звездочный обзор, чтобы мы могли продолжать обновлять замечательные новые функции!

НАЧНИТЕ РАСЧЕТЫ СЕГОДНЯ

29 марта 2022 г.

Версия 1.38

— Исправлены мелкие ошибки и улучшена производительность.

Было бы здорово услышать ваши отзывы по адресу [email protected]

Рейтинги и обзоры

5,7 тыс. оценок

Идеальная замена известкового

Теперь, когда у ipad нет калькулятора по умолчанию, это идеальная замена. Калькулятор, который прост, быстр, хорошо выглядит (со светлой и темной опцией) и….. Без рекламы!!!!!!!!!!! Чуть не забыл — и бесплатно. ИДЕАЛЬНЫЙ!!!!!!! Каждый должен получить это, если им не нужны более научные варианты или реклама.

За 10 лет я, наверное, написал только 3 отзыва. Я просто не беру или не имею на это времени, но это нужно было сделать. С ооочень большим количеством доступных опций (приложений), но все же так сложно быстро и легко найти то, что вам действительно нужно и/или нужно, другие должны знать, это одно из тех приложений, которые вы хотите установить и сохранить!!!!

Спасибо за вдохновение! Мы делаем все возможное, чтобы сделать его лучше.

Отличный калькулятор ПОЧТИ, но поддержка???

Я наслаждался этим калькулятором до сегодняшнего дня. Случайно нажал «С». К счастью, есть История! НО… Я не могу понять, как легко использовать историю для восстановления длинного расчета. Я могу перепечатать каждый элемент снова, но для этого не нужна история! Я легко «скопирую уравнение целиком», но не могу найти способ «вставить» уравнение. ТАК… вернулся в App Store (потому что в приложении нет явной ПОМОЩИ) и нажал на поддержку. Это привело меня к рекламе, отзывам и подключению к Facebook. Никакой помощи, которую я мог видеть. Поскольку у меня больше нет Facebook из соображений безопасности, я не мог видеть, есть ли там ПОМОЩЬ.
Поскольку я выбрал это приложение главным образом из-за его возможностей по истории, я, к сожалению, разочарован. Я надеюсь, что кто-то там может помочь мне понять это. Когда вы устали от кажущихся бесконечными математических вычислений, легко хотя бы на время забыть, как использовать простое в остальном приложение. Несмотря на это, должен быть легкодоступный и очевидный раздел справки для ответов на вопросы. Это, на мой взгляд, сделало бы этот калькулятор идеальным!
Пожалуйста, помогите!

Спасибо за отзыв! Мы учтем ваши предложения. Существует способ скопировать уравнение и вставить его снаружи (например, некоторые заметки и т. д.). В настоящее время в приложении нет функций для вставки, но вы всегда можете редактировать уравнение во время расчета.

Окончательно! Правильный калькулятор!

Я перепробовал все приложения-калькуляторы. Этот правильно понял! Я хотел базовый, с цифрами в правильном положении и с возможностью просмотра истории. Успешно справился! Реклама не раздражает, но я посмотрю, есть ли платная версия по разумной цене. Что-то хорошее добавить было бы больше выбора цвета. Приложение по-прежнему стоит 5 звезд, как оно есть.

Спасибо за отзыв! Мы очень рады, что вам нравится приложение, оставайтесь с нами, чтобы получить больше 💕

Разработчик Otrofy Inc. указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.

Данные, используемые для отслеживания вас

Следующие данные могут использоваться для отслеживания вас в приложениях и на веб-сайтах, принадлежащих другим компаниям:

Данные, не связанные с вами

Могут быть собраны следующие данные, но они не связаны с вашей личностью:

Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше

Информация

Продавец

Отрофи Инк.

Размер

59,4 МБ

Категория

Финансы

Возрастной рейтинг

4+

Авторское право

© Otrofy Inc.