Опубликовано Сложение двоичных чисел онлайн
Назначение сервиса. Онлайн-калькулятор предназначен для сложения двоичных чисел в прямом, обратном и дополнительном кодах.- Решение онлайн
- Видеоинструкция
- Также решают
Число №1
Число №2
Числа представлены в 102 системе счисления.Операция с числами СложениеВычитание Для дробных чисел использовать 2345678 знака после запятой.
Действие производить в: Прямом кодеОбратном кодеДополнительном кодеПодробнее.
Вместе с этим калькулятором также используют следующие:
Перевод чисел в двоичную, шестнадцатеричную, десятичную, восьмеричную системы счисления
Умножение двоичных чисел
Формат представления чисел с плавающей запятой
Пример №1.
Решение. Представим число 133.54 в нормализованном экспоненциальном виде:
1.3354*102 = 1.3354*exp102
Число 1.3354*exp102 состоит из двух частей: мантиссы M=1.3354 и экспоненты exp10=2
Если мантисса находится в диапазоне 1 ≤ M Представление числа в денормализованном экспоненциальном виде.
Если мантисса находится в диапазоне 0,1 ≤ M Представим число в денормализованном экспоненциальном виде: 0.13354*exp103
Пример №2. Представить двоичное число 101.102 в нормализованном виде, записать в 32-битом стандарте IEEE754.
Таблица истинности
Вычисление пределов
Арифметика в двоичной системе счисления
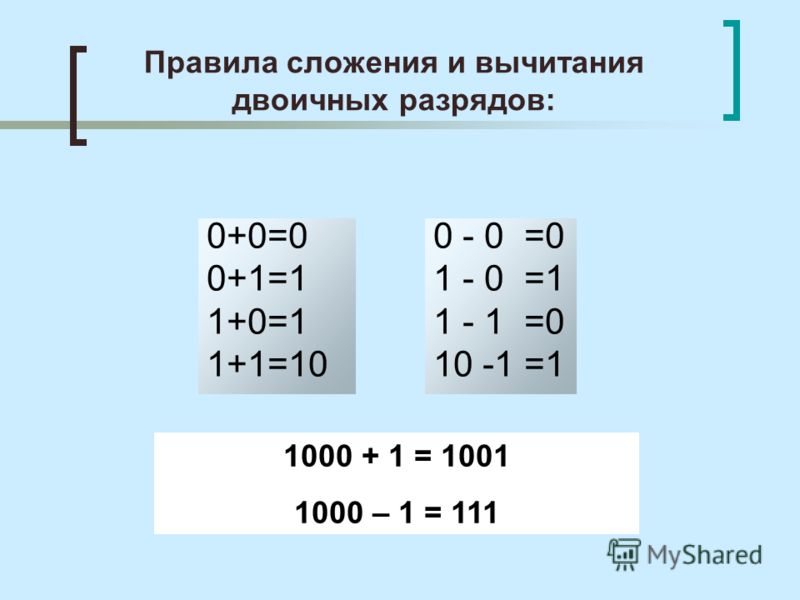
Арифметические действия в двоичной системе выполняются так же, как и в десятичной. Но, если в десятичной системе счисления перенос и заём осуществляется по десять единиц, то в двоичной — по две единицы.
В таблице представлены правила сложения и вычитания в двоичной системе счисления.
- При сложении в двоичной системе системе счисления двух единиц в данном разряде будет 0 и появится перенос единицы в старший разряд.
- При вычитании из нуля единицы производится заём единицы из старшего разряда, где есть 1. Единица, занятая в этом разряде, даёт две единицы в разряде, где вычисляется действие, а также по единице, во всех промежуточных разрядах.
| Сложение
0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10 |
Вычитание
0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 10 – 1 = 1 |
Сложение чисел с учетом их знаков на машине представляет собой последовательность следующих действий:
- преобразование исходных чисел в указанный код;
- поразрядное сложение кодов;
- анализ полученного результата.
При выполнении операции в дополнительном (модифицированном дополнительном) коде если в результате сложения в знаковом разряде возникает единица переноса, она отбрасывается.
Операция вычитания в ЭВМ выполняется через сложение по правилу: Х-У=Х+(-У). Дальнейшие действия выполняются также как и для операции сложения.
Пример №1.
Дано: х=0,110001; y= -0,001001, сложить в обратном модифицированном коде.
Пример №2. Решить примеры на вычитание двоичных чисел, используя метод дополнения до 1 и циклического переноса.
а) 11 — 10.
Решение.
Представим числа 112 и -102 в обратном коде.
Обратный код для положительного числа совпадает с прямым кодом.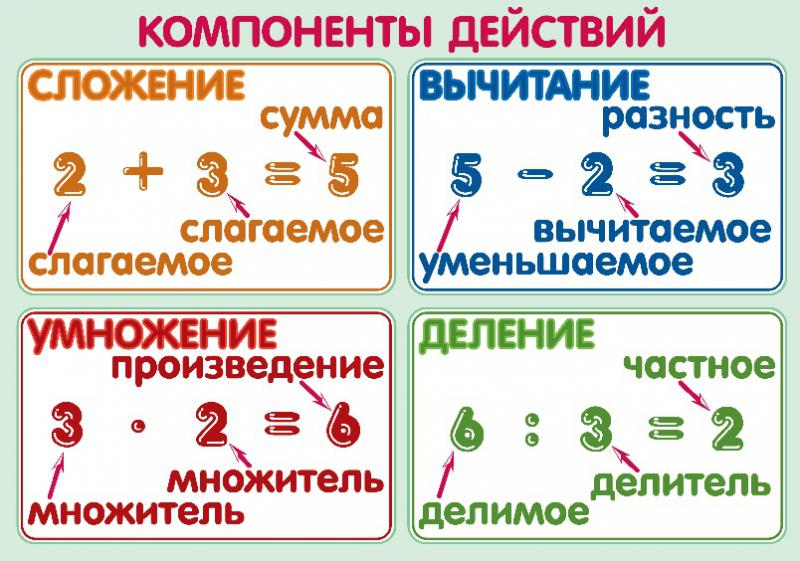
Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 0000011 имеет обратный код 0,0000011
Двоичное число 0000010 имеет обратный код 1,1111101
Сложим числа 00000011 и 11111101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 |
В 1-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 2-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 |
В 2-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 3-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 |
В 3-ом разряде возникло переполнение (1 + 1 = 10).
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 |
В 4-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 5-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
В 5-ом разряде возникло переполнение (1 + 1 = 10).
Поэтому записываем 0, а 1 переносим на 6-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
В 6-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 7-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В 7-ом разряде возникло переполнение (1 + 1 = 10).
Поэтому записываем 0, а 1 переносим на 8-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Возник перенос из знакового разряда.
Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Результат сложения: 00000001. Переведем в десятичное представление. Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000001 = 27*0 + 26*0 + 25*0 + 24*0 + 23*0 + 22*0 + 21*0 + 20*1 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 1 = 1
Результат сложения (в десятичном представлении): 1
б) 111-010
Представим числа 1112 и -0102 в обратном коде.
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 0000111 имеет обратный код 0,0000111
Двоичное число 0000010 имеет обратный код 1,1111101
Сложим числа 00000111 и 11111101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 |
В 1-ом разряде возникло переполнение (1 + 1 = 10).
Поэтому записываем 0, а 1 переносим на 2-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 |
В 2-ом разряде возникло переполнение (1 + 1 + 1 = 11). Поэтому записываем 1, а 1 переносим на 3-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | |||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 |
В 3-ом разряде возникло переполнение (1 + 1 = 10).
Поэтому записываем 0, а 1 переносим на 4-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 |
В 4-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 5-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 |
В 5-ом разряде возникло переполнение (1 + 1 = 10).
Поэтому записываем 0, а 1 переносим на 6-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 |
В 6-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 7-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
В 7-ом разряде возникло переполнение (1 + 1 = 10).
Поэтому записываем 0, а 1 переносим на 8-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Возник перенос из знакового разряда.
Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
Результат сложения: 00000101
Получили число 00000101. Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000101 = 27*0 + 26*0 + 25*0 + 24*0 + 23*0 + 22*1 + 21*0 + 20*1 = 0 + 0 + 0 + 0 + 0 + 4 + 0 + 1 = 5
Результат сложения (в десятичном представлении): 5
Сложение двоичных вещественных чисел с плавающей запятой
В компьютере любое число может быть представлено в формате с плавающей точкой.
Формат с плавающей точкой показан на рисунке:
Например, число 10101 в формате с плавающей точкой можно записать так:
В компьютерах используется нормализованная форма записи числа, в которой положение запятой всегда задается перед значащей цифрой мантиссы, т.е. выполняется условие:
b-1≤|M|<b0=1
Нормализованное число — это число, у которого после запятой идет значащая цифра (т.е. 1 в двоичной системе счисления). Пример нормализации:
0,00101*2100=0,101*210
111,1001*210=0,111001*2101
0,01101*2-11=0,1101*2-100
11,1011*2-101=0,11011*2-11
При сложении чисел с плавающей точкой выравнивание порядков выполняют в сторону большего порядка:
Алгоритм сложения чисел с плавающей точкой:
- Выравнивание порядков;
- Сложение мантисс в дополнительном модифицированном коде;
- Нормализация результата.
Пример №4.
A=0,1011*210, B=0,0001*211
1. Выравнивание порядков;
A=0,01011*211, B=0,0001*211
2. Сложение мантисс в дополнительном модифицированном коде;
MAдоп.мод.=00,01011
MBдоп.мод.=00,0001
00,01011
+ 00,00010
=
00,01101
A+B=0,01101*211
3. Нормализация результата.
A+B=0,1101*210
Пример №3. Записать десятичное число в двоично-десятичной системе счисления и сложить два числа в двоичной системе счисления.
Калькулятор вероятностного закона сложения — MathCracker.com
Вероятность Решатели Статистика
Инструкции: Используйте этот калькулятор закона сложения для вычисления вероятности \(\Pr(A \cup B)\).
Пожалуйста, укажите вероятности \(\Pr(A)\), \(\Pr(B)\) и \(\Pr(A \cap B)\) в форме ниже:
Укажите значение \(\Pr(A)\) =
Укажите значение \(\Pr(B)\) =
Укажите значение \(\Pr(A \cap B)\) =
Закон сложения — одна из самых основных теорем теории вероятностей. Он принимает очень четкую форму при изображении на диаграмме Венна: идея состоит в том, что, когда мы подсчитываем вероятности для A или B, когда мы складываем \(\Pr(A)\) и \(\Pr(B)\), бывает, что мы считаем дважды ту часть, которая соответствует \(\Pr(A \cap B)\).
Следовательно, Закон сложения принимает следующую форму:
\[\Pr(A \cup B) = \Pr(A) + \Pr(B) — \Pr(A \cap B) \]
Обратите внимание, что, переставляя приведенное выше выражение, мы попадаем в одну версию закона умножения для вероятностей.
\[\Pr(A \cap B) = \Pr(A) + \Pr(B) — \Pr(A \cup B) \]
Калькулятор закона сложения Закон сложения вероятностей Калькулятор вероятностей Правило вероятности сложения Калькулятор статистики Статистический решатель
Калькулятор сложений
Автор: Доминика Смялек, доктор медицинских наук, кандидат наук
Отзыв: Доминик Черня, доктор наук, и Джек Боуотер
Последнее обновление: 09 января 2023 г.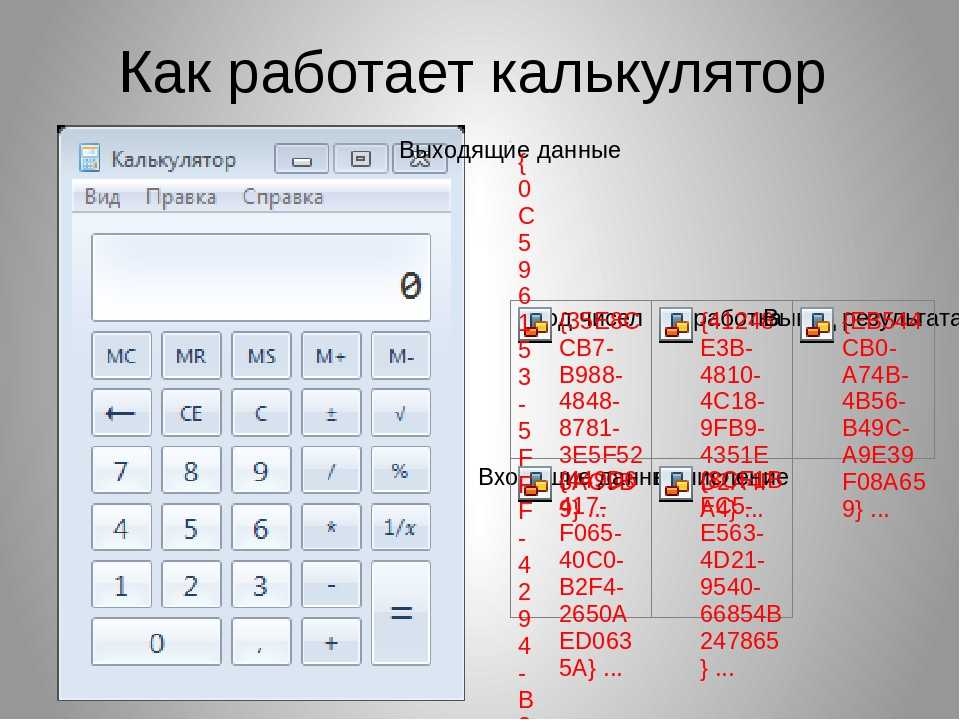
Вам когда-нибудь приходилось складывать два действительно больших числа, а под рукой не было удобного калькулятора? С этим 9Калькулятор сложения 0019, вы всегда сможете легко сложить два числа , будь они положительными или отрицательными, большими или маленькими. В приведенной ниже статье мы объясним, как работает наш калькулятор суммирования, и предоставим вам раздел, чтобы вы могли ознакомиться с определением сложения.
Если вы хотите округлить полученное число, будь то десятичное число или просто слишком большое, тогда наш калькулятор округления может оказаться именно тем инструментом, который вам нужен!
Математика определения сложения — что такое сложение?
Суммирование, также называемое сложением, представляет собой процесс вычисления суммы двух (или более) слагаемых. Что такое дополнение? Те числа, которые складываются вместе, называются слагаемыми , которые в нашем калькуляторе отмечены как A и B .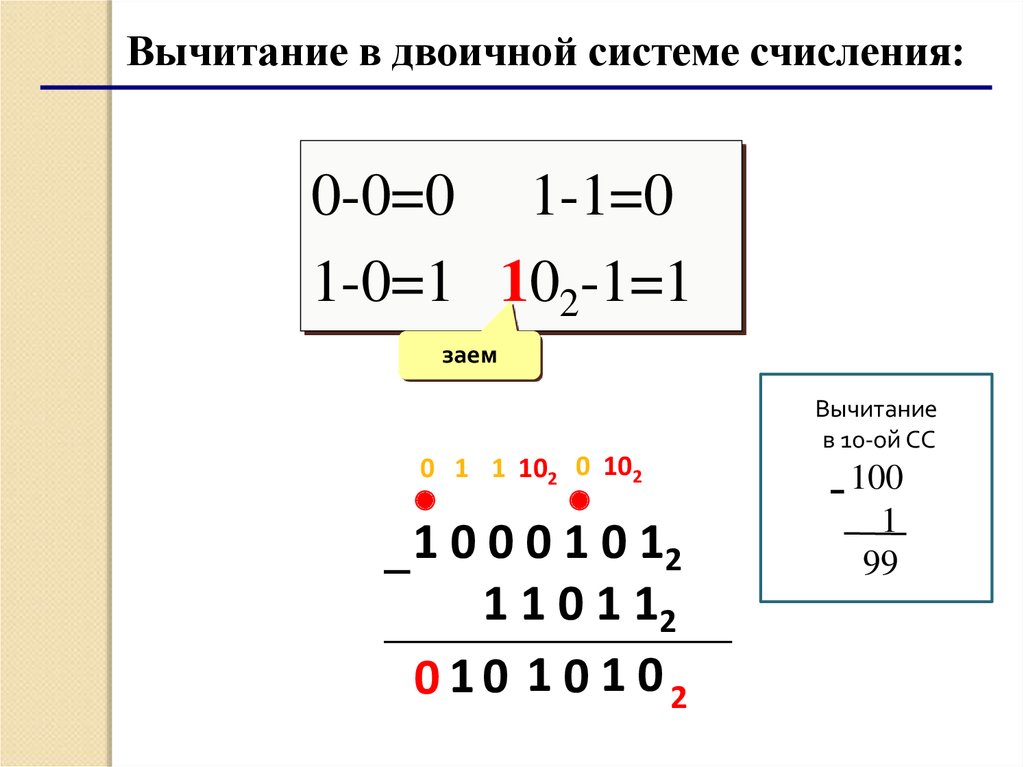
Результат этого процесса называется суммой , в этом калькуляторе сложения известен как C .
Сложение — одна из четырех основных арифметических операций, наряду с:
- Вычитание;
- Умножение; и
- отдел.
Символ сложения — плюс (➕), и мы помещаем его между двумя слагаемыми. Есть обозначения, в которых это неверно: проверьте наш конвертер польских обозначений!
Сложение имеет два свойства: коммутативность и ассоциативность.
Коммутативность означает, что вы можете поменять местами слагаемые без изменения результата уравнения, A + B = B + A .
Ассоциативность , с другой стороны, становится важным, когда мы пытаемся сложить более двух чисел. Это означает, что не имеет значения, прибавляете ли вы первое число ко второму, а затем третье или третье ко второму, а затем к первому. Результат не изменится, A + (B + C) = (A + B) + C .
Если вы продолжаете добавлять +1, имя процесса будет , считая . Кроме того, хорошо понимать, что вы можете добавить 0, хотя это вычисление не меняет результат. В случае, если уравнение требует добавления отрицательных чисел, вычтите отрицательное значение из исходной цифры: A + (-B) = A - B
🙋 Хотите научиться решать сложные математические задачи, включающие более одной арифметической операции? Проверьте наш калькулятор распределительной собственности.
Добавить номера — не так просто?
Звучит тривиально. Таким образом, математика сложения дает вам такое простое определение, как вы думали, — добавьте число к другому, и вы получите результат. Однако, поскольку ты здесь, мы оба знаем, что это может быть не так просто. Иногда цифры огромные. Другой вариант заключается в том, что они отрицательные или, может быть, дроби. Во всех этих ситуациях наш калькулятор работает безотказно и дает правильный ответ. Сложение также полезно при нахождении делимости числа с помощью калькулятора суммы цифр.
Самые ранние обнаруженные данные свидетельствуют о том, что сложение использовалось между 20 000 и 18 000 лет до нашей эры. К счастью, теперь, когда у вас есть наш калькулятор сложения, вам больше не нужно делать это вручную!
Калькулятор суммирования — как он складывает числа?
Это просто и интуитивно понятно. Заполните первое поле добавления (A) и второе поле добавления (B). Калькулятор сделает все остальное за вас и выдаст вам сумму (C).
A + B = C
Все может немного усложниться, если, например, у вас есть двоичное число или дробь. Если это дробь, то есть решение. Вы можете либо переключить его на десятичный вид, либо воспользоваться нашим калькулятором сложения дробей.
Расширенное применение свойства суммирования можно найти в постулате сложения сегментов, который включает в себя нахождение длины сегмента, когда 3 точки лежат на одной прямой.
Калькулятор сложения на практике
Итак, давайте попрактикуемся на примере.
Представьте, что одно из ваших слагаемых равно A = 32948, а другое B = 2938546.
32948 + 2938546 = 2 971 494
Что произойдет, если B отрицательно?
32948 + -2938546 = -2 905 598
И все! 🎉
Dominika śmiałek, MD, кандидат PhD
A +B = C
Первое число (A)
Второе число (B)
Результат
Сумма (C)
Проверьте 63 аналогичные раскаты.
Абсолютное изменениеАбсолютное значениеАссоциативное свойство… Еще 60
Калькулятор сложения коэффициентов | iCalculator™
Калькулятор коэффициентов от iCalculator позволяет складывать два коэффициента вместе. Математический процесс сложения двух отношений или более двух отношений вместе называется сложением отношений. Этот калькулятор сложения коэффициентов автоматически рассчитает сумму двух коэффициентов, эквивалентного целого числа и эквивалентной дроби, как часть расчетов коэффициента. Каждый шаг расчета коэффициента отображается так, что вы можете проверить свои собственные расчеты сложения коэффициента вместе с калькулятором.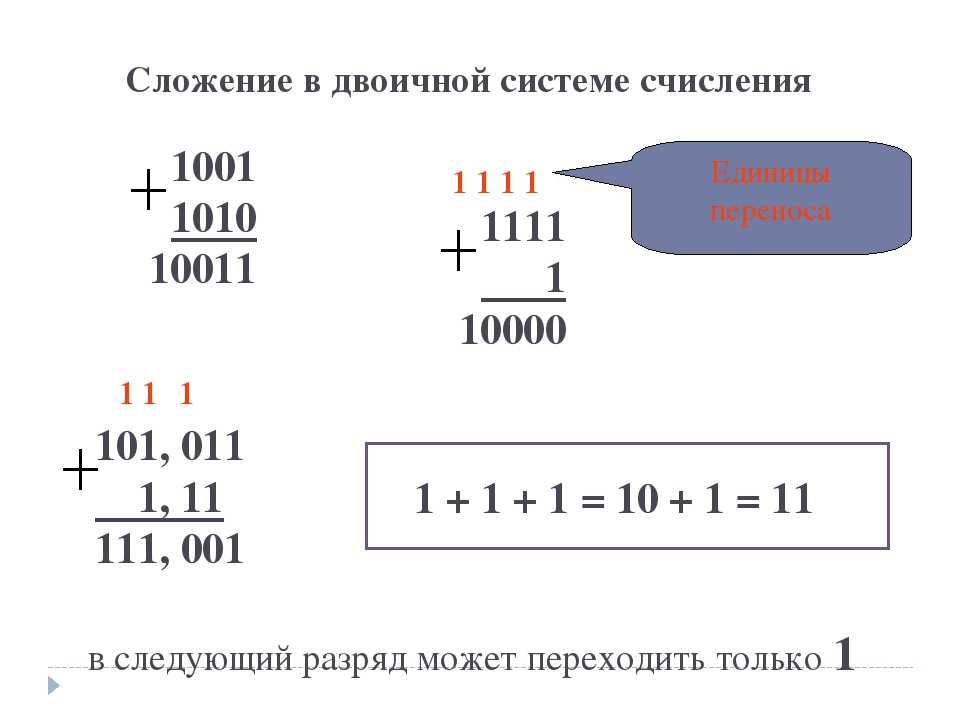
| Calculator Precision (Decimal Places)0123456789101112131415 |
| Ratio a Numerator ( a n ) : Ratio a Denominator ( a d ) |
| : |
| + |
| : |
★ ★ ★ ★ ★ [ 204 Голоса ] 3 3 3 3 Что такое Ratios?
С точки зрения математики, отношение — это относительная величина, которая выражается двумя или более числами, разделенными двоеточием, например, соотношение двух чисел записывается как 3:4 или отношение с более чем двумя числами, давайте использовать четыре Например, соотношение чисел записывается как 6:2:9:45, где каждое число отделяется двоеточием.
Как рассчитать коэффициенты?
В следующих примерах показано, как выполнять математические операции с отношениями.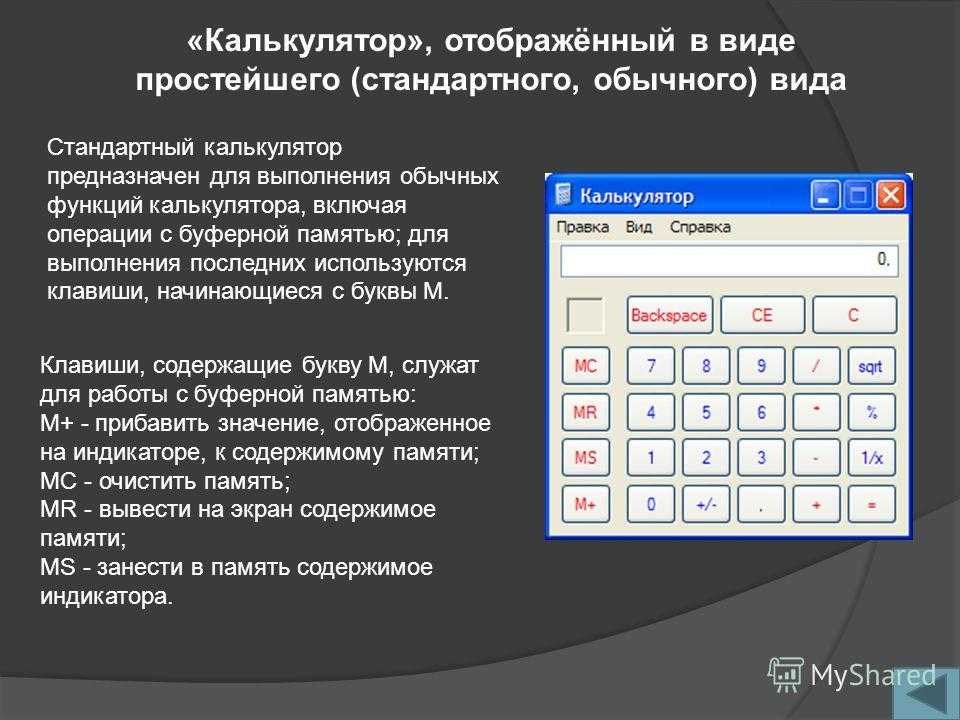
Как складывать отношения
Хитрость при сложении отношений заключается в том, чтобы следить за числом справа от двоеточия (:), это число называется знаменателем отношения . Когда знаменатель обоих отношений один и тот же, сложение отношения просто. Вы просто добавляете числа слева от двоеточия (это число называется числителем отношения ).
Коэффициент сложения Пример 1: 1:3 + 1:3 = 2:3 Легко, а?
Теперь сложение отношений становится немного (но только немного) более сложным, когда знаменатели (число справа от двоеточия) складываемых отношений не совпадают. Существует простое правило при сложении коэффициентов: номиналы всегда должны быть одинаковыми, в математических терминах это называется общим знаменателем , поскольку все знаменатели имеют одно и то же «общее» значение.
Итак, вы пытаетесь сложить отношение с разными знаменателями, и вам нужен общий знаменатель, как вы его получите? Если вы работаете с двумя отношениями, вы можете найти общий знаменатель, просто перемножив знаменатели:
Пример сложения отношения 2 Шаг 1: 2:5 + 3:4, наши два знаменателя равны 5 и 4.
Пример расчета отношения 2 Шаг 2: 5 x 4 = 20 Общий знаменатель.
Понял? Большой. Теперь, чтобы сделать наши исходные коэффициенты эквивалентными коэффициентами . Примечание: вы можете узнать больше об эквивалентных коэффициентах и о том, как рассчитать эквивалентные коэффициенты здесь.
Эквивалентное отношение — это соотношение одного и того же значения, записанное в другом формате, например, 1:2 равно 2:4 и 5:10.
Чтобы сделать наши соотношения эквивалентными, мы должны выполнить то же действие с верхним числом (числителем), что и с нижним числом (знаменатель)
Пример расчета отношения 2 Шаг 3: 5 x 3 = 15 Мы умножаем 3 на 5 так же, как ранее умножали 4 на 5.
Расчет соотношения Пример 2 Шаг 4: 15:20 эквивалентно соотношению 3:4.
Затем мы повторяем упражнение для нашего другого отношения
Пример расчета отношения 2 Шаг 5: 4 x 2 = 8 Мы умножаем 2 на 4, как ранее умножали 5 на 4.