Решение десятичных уравнений онлайн калькулятор
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Линейное уравнение с десятичными дробями решается точно так же, как и множество других уравнений, однако их решение нужно начинать с сокращения уравнения и избавления от десятичных дробей.
Так же читайте нашу статью «Решить дифференциальное уравнение онлайн»
Допустим, дано уравнение следующего вида:
\[2,4(6 — 3x) + 4,3 = 1,7 — 5,2x\]
Данное уравнение можно решить двумя разными способами.
Способ № 1:
Решение начинаем с упрощения уравнения с помощью открытия скобок, а поскольку перед скобками у нас стоит число, то умножаем это число на каждый член в скобках:
\[14,4 — 7,2x + 4,3 = 1,7 — 5,2x\]
Сейчас наше уравнение имеет линейный вид, благодаря чему мы производим перенос неизвестных в одну сторону, целый числе в другую:
\[ — 7,2x + 5,2x = 1,7 — 14,4 — 4,3\]
Делим 2 части на число перед \[x :\]
\[ — 2x = — 17\]
Ответ: \[x = 8,5. \]
\]
Способ № 2:
В этом способе умножим левую и правую части на 10:
\[2,4(6 — 3x) + 4,3 = 1,7 — 5,2x\]
\[24(6 — 3x) + 43 = 17 — 52x\]
Это линейное уравнение, которое решается по аналогии с 1 способом:
\[144 — 72x + 43 = 17 — 52x\]
\[ — 72x + 52x = 17 — 144 — 43\]
\[ — 20x = — 170\]
Ответ: \[x = 8,5.\]
Где можно решить десятичные уравнения онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher.
Решение уравнений с десятичными дробями
1. «Решение уравнений с десятичными дробями» 5 класс
2. Реши уравнение:
К. 4х = 0,22+0,26;Т. 5х = 8,17+2,48;
З. 6х = 3,9*8;
Х. 7х-4х = 0,96;
А. х+2х = 21,42;
С. 2х+5х = 42,7;
Н. 12х-3х = 41,4.
0,12
7,14
5,2
7,14
0,32
6,1
2,13
7,14
4,6
3. Прогулка в лес
Вы бывали летом в лесу?Прогулка по лесу – это так приятно,
а наблюдательному человеку ещё и
интересно!
4. «На опушке леса»
5. Сформулируйте правила нахождения неизвестных компонентов в уравнении.
Как найти неизвестноеКак умножить десятичную
дробь на 0,1; 0,01; 0,001?
8. Сформулируйте правило умножения десятичных дробей.
Что надо сделать приумножении на десятичную
дробь, если в произведении
меньше цифр, чем надо
отделить запятой?
«Собери грибы в лукошко»
Лес – это кладовая, щедро отдающая свои дары.

11. Поставьте запятые в произведении
2,31 ∙ 5,4 = 12474;,
2,31 ∙ 0,54 = 12474;
,
23,1 ∙ 5,4 = 12474;
,
0,231 ∙ 54 = 12474;
,
0,231 ∙ 0,54 =0, 12474.
проверить
12. «Молчанка»
6,7 ∙ 8,4 + 6,7 ∙ 1,643,2
12,37 ∙ 4,185 – 12,37 ∙ 3,185
67
6,1 ∙ 3,4 + 6,1 ∙ 2,6
36,6
9,1 ∙ 0,387 – 9,1 ∙ 0,287
12,37
0,5 ∙ 43,2 ∙ 2
6,2711
1,25 ∙ 3,27 ∙ 8
4,516
62,711 : 10
0,91
451,6 ∙ 0,01
32,7
13. «В гостях у Старичка – лесовичка»
-А у меня для вас задание припасено.Если выполните его, то смело заходите
в глубь леса!
14. «Привал»
0,3 · 2,253,03 ∙ 0,01
1,05 ∙ 5,27
2,8 ∙ 6,28
4,2 ∙ 6,3
7,3 ∙ 4
17,3 · 12,25
1,103 · 2,65
20,3 · 0,2
0,0003 ∙ 1,2
10,5 ∙ 4,2
3 · 2,2
15. «На лесной полянке» Лес – это источник радости и здоровья.
Хвоя сосныВы можете
158,6
Зверобой
16,362
Земляника
лесная
Медуница
лекарственная
2,08
Крапива
0,74
Подорожник
1,44
1,08
Узнай, какое растение леса — клад витаминов.
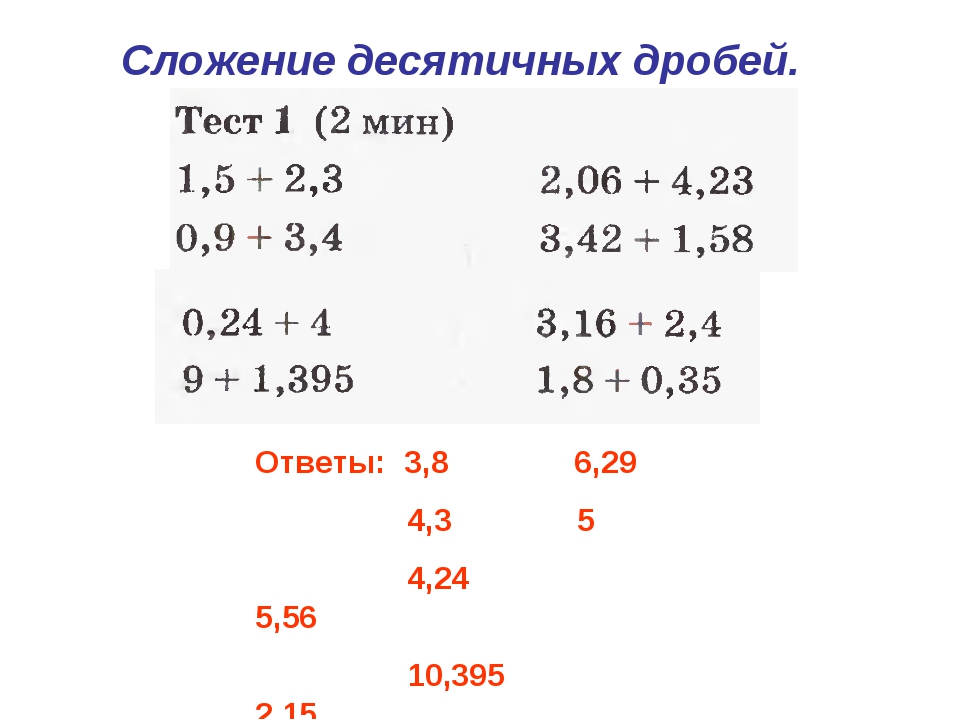
Для этого найди корень уравнения:
(х + 2,4) : 0,8 = 5,6
Узнай, какое растение леса — клад витаминов.
Для этого найди корень уравнения:
(х + 2,4) : 0,8 = 5,6
Плоды растения издревле употребляются человеком
в пищу. Водный настой листьев земляники лесной
применяются в качестве мочегонного средства при
мочекаменной и желчнокаменной болезнях. Их
употребление также назначается при диабете и
малокровии. Плоды применяют как витаминное
средство.
Это зелье ты не тронь:
Жжется больно, как огонь.
Ответь на вопрос, решив уравнение.
(3,5 — х) : 2,3 = 1,2
19. О каком растении говорится в загадке? Это зелье ты не тронь: Жжется больно, как огонь. Ответь на вопрос, решив уравнение.
(3,5 — х) : 2,3 = 1,2Крапива используется в народной медицине для
лечения многих болезней, применяется при
различных кровотечениях, почечнокаменной,
желчекаменной болезни, удушье, болезнях печени и
желчных путей, отеках, заболеваниях сердца,
туберкулезе, бронхиальной астме,
бронхитах, аллергиях.
 Наружно крапиву
Наружно крапивуиспользуют при открытых ранах,
кровотечениях, кожных заболеваниях, для
укрепления и роста волос.
Если ты порезал ногу, не рыдай и не реви.
Вот растенье на подмогу. Ты скорей его зови!
Что это за растение? Правильное решение уравнения
поможет ответить на этот вопрос.
х : 4,8 + 3,6 = 3,9
21. Если ты порезал ногу, не рыдай и не реви. Вот растенье на подмогу. Ты скорей его зови! Что это за растение? Правильное решение
уравненияпоможет ответить на этот вопрос.
х : 4,8 + 3,6 = 3,9
Настой из листьев подорожника обладает
отхаркивающим свойством, благодаря чему и
используется при лечении бронхитов, бронхиальной
астмы, туберкулеза легких. Сок свежих листьев
подорожника эффективен в лечении язвенной
болезни желудка и двенадцатиперстной кишки,
хронических гастритов. А водный настой
свежих листьев способствует быстрому
очищению и лечению ран, порезов,
кожных язв, нарывов и фурункулов.

Назови растение, имеющее репутацию лекарства от
100 болезней.
Реши уравнение и узнай ответ.
х : 2,7 — 5,16 = 0,9
Назови растение, имеющее репутацию лекарства от
100 болезней.
Реши уравнение и узнай ответ.
х : 2,7 — 5,16 = 0,9
Зверобой применяют для лечения многих
недугов: в качестве антисептического средства,
для смазывания десен и полосканий, при
анемии, при лечении пролежней, аллергии, ран,
язв, сыпи, при болезнях мочевого пузыря,
желудочно-кишечного тракта, болезнях почек,
гриппе, слабости сердца, простудных
заболеваниях, туберкулезе, для лечения мастита,
желтухи, кашля, желудочных и легочных
заболеваний, мигрени, при язве желудка,
головной боли, нервных болезнях, повышенной
кислотности желудочного сока.
24. «Заветная тропинка»
Чтобы выйти из леса и вернутьсядомой, вы должны проявить
самостоятельность, показать волю и
упорство.
25. Итог урока
Домашнее задание:1 уровень: № 1476, № 1482,
2 уровень: № 1475, № 1513;
Решение квадратных уравнений онлайн
С помощю этого онлайн калькулятора можно найти решение (корни) квадратного уравнения. Дается подробное решение с пояснениями. Для нахождения решений квадратного уравнения введите коэффициенты уравнения и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Корни квадратного уравнения − теория примеры и решения
Квадратным уравнением называется уравнение следующего вида:
где x−переменная, а a, b, c некоторые числа (a≠0). Числа a, b, c называются коэффициентами квадратного уравнения. Коэффицинт c называется свободным членом.
Числа a, b, c называются коэффициентами квадратного уравнения. Коэффицинт c называется свободным членом.
Если a=1, то квадратное уравнение называется приведенным. Заметим, что любое квадратное уравнение можно привести к приведенному виду, разделив обе части уравнения на
Если в квадратном уравнении (1) один из коэффициентов b, c равен нулю или оба коэффициента b, c равны нулю, то квадратное уравнение называется неполным.
Рассмотрим разные виды неполных квадратных уравнений.
1. При b=0 имеем:
Для решения этого уравнения свободный член перенесем в правую часть уравнения:
Решая последнее уравнение относительно x получим корни квадратного уравнения (3):
Если , то квадратное уравнение не имеет действительных корней.
2. При c=0 имеем:
Разложим левую часть последнего уравнения на множители:
Из (4) следует x=0 или ax+b=0. Следовательно имеем следующие решения:
Следовательно имеем следующие решения:
3. При b=0, c=0 имеем:
и, следовательно
Рассмотрим, далее, алгоритм решения квадратных уравнений общего вида (1). Разделим обе части уравнения на a:
Сделаем эквивалентные преобразования уравнения (5):
Легко догадаться, что первые три слагаемые уравнения (6) образуют квадрат следующей суммы:
Тогда
Обозначим
D− называется дискриминантом квадратного уравнения (1). Так как a≠0, то 4a2>0. Знак правой части уравнения (7) определяется знаком дискриминанта D.
Учитывая (8) запишем (7) в следующем виде:
При решении последнего уравнения возможны следующие варианты:
1. При D>0, имеем
Таким образом, при D>0, квадратное уравнение (1) имеет две корни:
2.При D=0, имеем
То есть, при D=0 квадратное уравнение (1) имеет единственный корень:
3.
Пример 1. Решить квадратное уравнение
| . | (10) |
Решение. Запишем коэффициенты квадратного уравнения (10):
Вычислим дискриминант квадратного уравнения:
| . |
Дискриминант положительное число. Следовательно квадратное уравнение (10) имеет два решения.
Найдем решение квадратного уравнения используя следующую формулу:
| . | (11) |
Подставляя значения коэффициентов a, b, c, D в (11), получим:
| , |
| . |
Ответ:
Пример 2. Решить следующее квадратное уравнение:
| . | (12) |
Решение. Запишем коэффициенты квадратного уравнения (12):
Вычислим дискриминант квадратного уравнения:
. |
Дискриминант равен нулю. Следовательно квадратное уравнение (12) имеет единственное решение. Найдем решение квадратного уравнения используя следующую формулу:
| . | (13) |
Подставляя значения коэффициентов a, b, c, D в (13), получим:
| , |
Ответ:
| . |
Пример 3. Решить следующее квадратное уравнение:
| . | (14) |
Решение. Запишем коэффициенты квадратного уравнения (14):
Вычислим дискриминант квадратного уравнения:
| . |
Дискриминант отрицательное число. Следовательно квадратное уравнение (14) не имеет действительных корней.
Ответ: Квадратное уравнение не имеет действительных корней.
№ | Этапы урока | Деятельность учителя | Деятельность ученика | |
1. | Организационный этап. | Приветствие детей. | Дети, приступившие к обучению, поднимают ладошку . Каждому ребёнку даётся по 2-3 секунды для приветствия. | |
2. | Постановка цели и задач урока. Мотивация учебной деятельности учащихся. Задачи: Организовать самоопределение детей к деятельности на уроке. эмоциональный настрой. | — Вступительное слово: Ребята, вы отлично поработали с заданиями на сайте Учи.ру. Команда сайта отметила вашу активность грамотами. Надеюсь, что сегодня мы с таким же боевым настроем будем систематизировать полученные знания. Объявляет тему урока. Мы сегодня будем работать командами. Команда девочек , команда мальчиков Каждый ученик, правильно ответивший на вопрос будет в чате получать цветок своей команды. | Кто готов к уроку, поднимите | |
3. | Первичное закрепление в знакомой ситуации (типовые) | Спрашивает, как можно объяснить правила вычисления десятичных дробей. Спрашивает, кому из учащихся нужно ещё раз повторить данные темы. Если возникают вопросы, повторяет на примере данную тему. | Комментируют Предполагаемый правильный ответ: Если записать десятичные дроби «в столбик» так, что запятая окажется под запятой, то будет выполняться поразрядное сложение чисел. Что для наглядности можно написать незначащие нули после запятой в одном из чисел, чтобы уровнять в числа количество знаков после запятой. Главное, чтобы при записи в столбик запятая оказалась под запятой. Комментируют Предполагаемый правильный ответ: Если при умножении на 10,100,1000 запятая переносится вправо на столько цифр, сколько нулей. При делении влево…. Комментируют. Предполагаемый правильный ответ: Напоминает, что при умножении в столбик запись чисел производится, не обращая внимания на запятые. После вычисления, влево отсчитывается столько цифр, сколько цифр всего после запятой. | |
Предлагает учащимся выполнить задание, чтобы систематизировать знания по темам «Действия с десятичными дробями» и «Решение уравнений». Команда Ромашка выполняет задания первого столбика, команда Колокольчик, задания второго столбика. Заполняет таблицу. | Выполняют задание учителя. Когда закончили работу, поднимают ладошку. Отвечают те, кому учитель даёт слово. | |||
4. | Контрольнооценочный этап | Изучает результаты выполнения теста учащимися, при необходимости даѐт дополнительные комментарии к выполненным заданиям. Вопрос 1 Поочерёдно даёт слово учащимся, поднявшим Заполняет таблицу. Если ученик даёт неправильный ответ, предлагает вспомнить и объяснить правило умножения, сложения, или вычитания дробей. Вопрос 2 Спрашивает, кто из учащихся согласен с этим предложением. Вопрос 3 Спрашивает, что интересного заметили в предложенных заданиях. Вопрос 4 Просит объяснить, ссылаясь на определения – «уравнения», «числовые выражения» Вопрос 5 Спрашивает каким способом пользовались,умножая на 11. | Изучают результаты проверки теста и комментарии к выполненным заданиям. Разбираются с допущенными ошибками. Все, кроме 12 и 6 заданий, уравнения Предполагаемый правильный ответ: Уравнение — это равенство, содержащее букву, значение которой надо найти. Числовое выражение – это любая запись из чисел, знаков арифметических действий и скобок. Одному ученику предоставляется возможность написать на доске и объяснить способ умножения на 11. | |
Зарядка для глаз. | Глазами следят за движениями воздушных шариков. | |||
5. | Творческое применение и добывание знаний в новой ситуации (проблемные задания) | Предлагает применить полученные знания по теме «Действия с десятичными дробями» при решении задач с помощью уравнений. Просит записать задачу так, чтобы учащиеся смогли ответить на вопросы после того, как текст задачи будет убран с экрана. 1. Предлагает ученикам кратко записать условие задачи, в виде схемы в тетради. 2. Предлагает поиск пути решения задачи и составление плана её решения. 3.Предлагает сделать проверку, обращает внимание на подчёркнутые числа в презентации. Просит поделиться своими соображениями учеников. | Отвечают на вопросы учителя. Выполняют краткую запись. Проверяют краткую запись по презентации. Предполагаемый правильный ответ: Поскольку одна из нужных нам величин для решения задачи неизвестна. Решаем задачу с помощью уравнения. Поочерёдно объясняют ход составления уравнения к задаче. Составленное уравнение один ученик пишет на доске. Решают уравнение в тетради. Один ученик у доски. Проверяют по презентации. Предполагаемый правильный ответ: Четыре одинаковых слагаемых можем заменит умножением. | |
Физкультминутка | Выполняют физкультминутку, повторяя движения мультипликационных героев. | |||
6. | Закрепление материала | Предлагает самостоятельно записать краткую запись задачи, составить уравнение и решить в тетради. Учитель записывает решение задачи под диктовку учащихся на доске, | Учащиеся, по одному, комментируют решение задачи, обращая внимание на правила сложения, умножения десятичных дробей. | |
7 | Рефлексия (подведение итогов занятия) | Оценка работы учащихся. Выставление оценок. Подведение итогов соревнования между командами Ромашка и Колокольчик. Просит выслать фото классной работы на почту или в ватсап. Обращается к учащимся: Наш урок подходит к концу. Скажите, вы не изменили своего мнения, по поводу отгадки кроссворда в начале урока? Подумайте о том, как всѐ происходило, что ты узнал и что ещѐ предстоит узнать? Сегодня я узнал(а)… На этом уроке мне было интересно… Сегодня я научился(научилась)… Мне ещѐ предстоит научиться… Тяжело ли было работать дистанционно? Когда интереснее на уроках? Примечание: Детям можно рекомендовать задание в учи ру «Решение текстовых . | Ученики, поднимают ладошку. Высказывают своё мнение. |
|
Номер задания КИМ |
Тема |
Просмотр видео-уроков |
|
1-5 |
Задачи практического содержания |
Экспресс подготовка от учи.ру: Смотреть Разбор задач ОГЭ (деление на типы) №1-№5 по ссылкам: 1 2 3 4 |
|
6 |
Вычисление значений выражений (оптимальное решение, не повышающее вероятность ошибки): обыкновенные и десятичные дроби |
Экспресс подготовка от учи. Смотреть |
|
7 |
Расположение чисел на координатной прямой: 1) Уметь сравнивать дроби (обыкновенные и десятичные) 2) При данных значениях переменных сравнивать с 0 их комбинацию (произведение, частное, сумму, разность, возведение в степень) |
Экспресс подготовка от учи.ру: Смотреть |
|
8 |
Вычисление значений выражений: 1) Степени с целым показателем и их свойства 2) Арифметический квадратный корень |
Экспресс подготовка от учи.ру: Смотреть |
|
9 |
Решение уравнений: 1) Линейные уравнения 2) Квадратные уравнения |
Экспресс подготовка от учи. Смотреть |
|
10 |
Теория вероятности, статистические характеристики |
Экспресс подготовка: Смотреть |
|
11 |
Графики функций (все виды функций): 1) Какой функции какая формула соответствует 2) Какому графику какая формула соответствует 3) Свойства функций |
Экспресс подготовка от учи.ру: Смотреть |
|
12 |
Задачи на прогрессии: 1) Арифметическая прогрессия 2) Геометрическая прогрессия |
Экспресс подготовка от учи.ру: Смотреть |
|
13 |
Преобразование выражений и нахождение их значений: 1) Выполнять разложение многочлена на множители различными способами 2) Выполнять совместные действия с алгебраическими дробями |
Экспресс подготовка от учи.ру: Смотреть |
|
14 |
Выражение переменной из формулы и отыскание значения этой переменной |
Экспресс подготовка от учи.ру: Смотреть |
|
15 |
Решение неравенств, выбрать промежуток, соответствующий заданному неравенству: 1) Линейные неравенства 2) Системы линейных неравенств 3) Квадратные неравенства |
Экспресс подготовка от учи.ру: Смотреть |
|
16 |
Простейшие задачи на нахождение градусных мер углов, длин отрезков |
Основные 8 типов задач с рассмотрением примеров каждого вида: Смотреть Общая подготовка №16 без классификации: Смотреть |
|
17 |
Простейшие задачи на нахождение элементов окружности |
Экспресс подготовка к ОГЭ: Смотреть |
|
18 |
Задачи на нахождение площади фигуры, изображенной на рисунке |
Задания на клетчатой бумаге, экспресс подготовка: Смотреть |
|
19 |
Задачи на нахождение тригонометрической функции от острого угла |
Рассмотрение 8 под тем, экспресс подготовка: Смотреть Все задания №19 из банка ФИПИ: Смотреть |
|
20 |
Определить истинность геометрических утверждений |
Рассмотрение типовых заданий: Смотреть |
|
21
|
Решение уравнений и систем уравнений: 1. Системы уравнений 2. Уравнения с заменой переменных 3. Уравнения высоких порядков (3, 4, 5, … степеней) 4. Неравенства 5. Прочее (не относящиеся ни к одному из видов) |
Экспресс подготовка от учи.ру: Смотреть и продолжение: Смотреть
|
|
22
|
Задачи на составление уравнений |
1. Задачи на движение. Экспресс подготовка от учи.ру: Смотреть 2. продолжение, задачи на проценты, сплавы, смеси: Смотреть |
|
23
|
Задачи на построение графиков |
Экспресс подготовка от Учи. Ру Смотреть Все задания №23 из ОГЭ (урок длится 4 часа): Смотреть |
|
24
|
Задачи на нахождение длин отрезков, градусных мер углов (геометрическая задача на нахождение неизвестной величины) |
Экспресс подготовка от учи.ру: Смотреть
|
|
25
|
Разные задачи на доказательство повышенного уровня сложности |
Рассмотрение доказательства типовых задач: Задача 1 типа: Смотреть Задача 2 типа: Смотреть Задача 3 типа: Смотреть Задача 4 типа: Смотреть Задача 5 типа: Смотреть Задача 6 типа: Смотреть |
|
26
|
Разные задачи по геометрии высокого уровня сложности. Комбинированные задачи вида: четырехугольник вписанный, или описанный около окружности; Нахождение расстояния от точки до прямой в четырехугольниках и т.д. |
Рассмотрение решения типовых задач: Задача 1 типа: Смотреть Задача 2 типа: Смотреть Задача 3 типа: Смотреть |
Десятичные дроби. Решение уравнений (презентация)
Урок-сказа ДЕСЯТИЧНЫЕ ДРОБИ. РЕШЕНИЕ УРАВНЕНИЙ
Денисова Светлана Ивановна
учитель математики
МОУ «Средняя школа №1»
г. Кимры Тверской области
В некотором царстве, в некотором государстве
Жил-был Иван-царевич
И было у него три сестры
АННА
МАРЬЯ
ОЛЬГА
Отдал Иван-царевич сестер своих замуж за царей
медного царства
серебряного царства
золотого царства
Целый год жил без сестер, и сделалась ему скучно. Решил он проведать сестриц
и отправился в путь дорогу
По дороге повстречал Елену Прекрасную
Они полюбили друг друга, но злой Кощей Бессмертный похитил Елену
Иван –царевич взял верных воинов и поехал выручать свою любимую
Вышли они к реке, а там огромный камень закрыл дорогу на мост
(y — 0,371)+ 5,44= 27,7
(0,127 + m) – 9,8= 3,2
(x + 0,379) – 1,97=1,83
Если их правильно решить, то камень повернется и освободит дорогу
Долго ехали они по лесу, пока дорога не привела их к избушке Бабы-Яги
2,4 – 3x = 0,21 (2)
2,5x + 0,8x = 99 (2)
5x – 7,35 = 0,3 (3)
7,2y – 0,3y = 27,6 (3)
Она долго враждовала с Кощеем и согласилась помочь Ивану-царевичу, но только в том случае, если его воины решат шесть уравнений
5,8y – 2,7y = 62 (1)
0,65 + 2x = 5,9 (1)
Прощаясь с Иваном-царевичем, Баба Яга рассказала ему о силе уравнения.
Коль нужно тебе какой запор отпереть или закрыть накрепко, произнеси вслух корни уравнения. Мигом исполнится.
Черный ворон подслушал этот разговор и рассказал обо всем Кощею.
Кощей подстерег Ивана –царевича и его воинов, схватил их и бросил в глубокое подземелье. Замкнул на шесть замков.
3,5 😡 – 2 = 1,5 (1)
(x – 0,5) * 5 =0,4 * 2 – 0,3 * 2 (1)
y: 0,2 + 0,35 = 3,6 (2)
(0,3 + x) * 4 = 0,3 * 3 + 0,7 * 3 (2)
m : 0,12 * 0,2 = 7,2 (3)
(0,7 + x) * 5 = 0,8 * 5 + 0,6 * 5 (3)
Иван-царевич произнес «волшебные слова», назвал корни всех уравнений. Двери подземелья открылись. Стали воины перед воротами Кощеева дворца
y + 0,0015 : 0,001 = 1,5
Ворота открылись Елена Прекрасная была освобождена и в тот же день сыграли свадьбу
После этого Иван-царевич вместе с Еленой прекрасной проведали его сестриц, приехали домой и стали жить –поживать и добра наживать
Конец сказки
Mathematica & Wolfram Language for Math Students—Fast Intro
Можно проводить факторизацию или раскрывать алгебраические выражения:
(Используйте CTRL+6 для ввода степени.5 == 0, x]| Out[2]= |
Функция Reduce сводит системы неравенств к простой форме:
(Наберите <= для ввода символа≤.)| In[1]:= | ⨯Reduce[{0 < x < 2, 1 <= x <= 4}, x] |
| Out[1]= |
Упрощенная форма может состоять из нескольких интервалов:
| In[2]:= | ⨯Reduce[(x - 1) (x - 2) (x - 3) (x - 4) > 0, x] |
| Out[2]= |
Функция NumberLinePlot — это удобный способ визуализации этих результатов:
| In[3]:= | ⨯NumberLinePlot[x < 1 || 2 < x < 3 || x > 4, {x, -10, 10}] |
| Out[3]= |
Большое число уравнений и формул доступно через естественную форму ввода:
| In[1]:= | Xquadratic equation |
| Out[1]= |
Справочная информация: Полиномиальные уравнения »
Справочная информация: Решение уравнений »
Hands–on Start to
Wolfram Mathematica »
Полная документация »
Demonstrations Project »
Калькулятор решения линейных уравнений
Онлайн-калькулятор решателя для линейных уравнений вида
\ (a x = b \), \ (a x + b = c x + d \) и \ (a (b x + c) = d (e x + f) \)
.
\ (a, b, c, d, e \; \ text {и} f \) — это коэффициенты, которые могут быть целыми, дробными или десятичными числами, вводимыми в калькулятор.
Калькулятор отображает уравнение и решение уравнения, если таковое имеется. При отображении уравнения десятичные числа сначала преобразуются в уменьшенные дроби.
Пример:
0,1 = 1/10
0,2 = 2/10 = 1/5
Этот калькулятор представляет собой самообучающийся инструмент, который поможет вам попрактиковаться в решении линейных уравнений с коэффициентами, которые могут быть целыми, десятичными и / или дробными значениями перечисленных выше типов. Вы можете задавать столько вопросов с ответами, сколько хотите, пока не овладеете навыками решения этих уравнений.
Калькулятор Решатель линейных уравнений вида: \ (a x = b \)
Введите a и b, а затем решите уравнение на бумаге.Когда закончите, нажмите «Решить». Отображаются уравнение и его решение. Проверьте свой ответ.
Коэффициенты \ (a \) и \ (b \) могут быть целым числом, например -2, дробью, например 3/4, или десятичным числом, например 0,1.
Обратите внимание на , что десятичные числа, если они есть, сначала преобразуются в уменьшенные дроби в отображаемых уравнениях.
Уравнение
Результат:
$ х = $
Калькулятор Решатель линейных уравнений вида: \ (a x + b = c x + d \)
Решите данное уравнение на бумаге, затем введите значения для \ (a, b, c \) и \ (d \), затем нажмите «Решить».Отображаются уравнение и его решение.
Коэффициенты a, b, c и d могут быть целыми числами, например -4, дробью scuh как -1/2 или десятичным числом, например 1,1.
Обратите внимание на , что десятичные числа, если они есть, сначала преобразуются в уменьшенные дроби в отображаемых уравнениях.
Уравнение
Результат:
$ х = $
Калькулятор Решатель линейных уравнений вида: \ (a (b x + c) = d (e x + f) \)
Введите \ (a, b, c, d, e \) и \ (f \), а затем решите уравнение на бумаге.Когда закончите, нажмите «Решить». Отображаются уравнение и его решение. Проверьте свой ответ.
Любой из коэффициентов \ (a, b, c, d, e \) и \ (f \) может быть целым числом, например -7, дробью, например -5/4, или десятичным числом, например 0,2.
Обратите внимание на , что десятичные числа, если они есть, сначала преобразуются в уменьшенные дроби в отображаемых уравнениях.
Уравнение
Результат:
$ х = $
Дополнительные ссылки и ссылки
Вопросы по решению линейных уравненийЕдинственные линейные уравнения с круглыми скобками с использованием закона распределения
Математические калькуляторы и решатели
| Автор | Сообщение | ||||||
|---|---|---|---|---|---|---|---|
| gockd Зарегистрировано: 18.05.2003 |
| ||||||
| Наверх | |||||||
| AllejHat Зарегистрирован: 16.07.2003 |
| ||||||
| Наверх | |||||||
| Vnode Зарегистрировано: 27.09.2001 |
| ||||||
| Наверх | |||||||
| SanG Зарегистрировано: 31.08.2001 |
| ||||||
| Наверх | |||||||
Двоичный калькулятор
Используйте следующие калькуляторы для выполнения сложения, вычитания, умножения или деления двух двоичных значений, а также для преобразования двоичных значений в десятичные значения и наоборот.
Двоичное вычисление — сложение, вычитание, умножение или деление
Преобразовать двоичное значение в десятичное
Преобразовать десятичное значение в двоичное
Калькулятор RelatedHex | Калькулятор IP-подсети
Двоичная система счисления — это система счисления, которая функционирует практически идентично десятичной системе счисления, с которой люди, вероятно, более знакомы. В то время как в десятичной системе счисления используется число 10 в качестве основы, в двоичной системе используется 2. Кроме того, хотя в десятичной системе используются цифры от 0 до 9, в двоичной системе используются только 0 и 1, и каждая цифра называется битом. .Помимо этих различий, такие операции, как сложение, вычитание, умножение и деление, все вычисляются по тем же правилам, что и десятичная система.
Почти все современные технологии и компьютеры используют двоичную систему из-за простоты ее реализации в цифровых схемах с использованием логических вентилей. Намного проще разработать оборудование, которое должно определять только два состояния: включено и выключено (или истина / ложь, присутствует / отсутствует и т. Д.). Использование десятичной системы требует оборудования, которое может определять 10 состояний для цифр от 0 до 9, что является более сложным.
Ниже приведены некоторые типичные преобразования между двоичными и десятичными значениями:
Двоичное / десятичное преобразование
| Десятичный | Двоичный |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
Работа с двоичным кодом может сначала показаться запутанной, Понимание того, что каждое двоичное разрядное значение представляет 2 n , так же, как каждое десятичное место представляет 10 n , должно помочь уточнить.Возьмем, к примеру, число 8. В десятичной системе счисления 8 находится в первом десятичном разряде слева от десятичной точки, что означает 10 0 место. По сути это означает:
8 × 10 0 = 8 × 1 = 8
Используя число 18 для сравнения:
(1 × 10 1 ) + (8 × 10 0 ) = 10 + 8 = 18
В двоичном формате 8 представлено как 1000. При чтении справа налево первый 0 представляет 2 0 , второй 2 1 , третий 2 2 и четвертый 2 3 ; точно так же, как десятичная система, за исключением того, что основание 2, а не 10.Поскольку 2 3 = 8, в его позиции вводится 1, что дает 1000. Используя 18 или 10010 в качестве примера:
18 = 16 + 2 = 2 4 + 2 1
10010 = (1 × 2 4 ) + (0 × 2 3 ) + (0 × 2 2 ) + (1 × 2 1 ) + (0 × 2 0 ) = 18
Пошаговый процесс преобразования десятичной системы в двоичную:
- Найдите наибольшую степень двойки, лежащую в пределах данного числа
- Вычтите это значение из данного числа
- Найдите наибольшую степень двойки в остатке, найденном на шаге 2
- Повторяйте до тех пор, пока не останется остаток
- Введите 1 для каждого найденного двоичного разряда и 0 для остальных
Снова используя цель 18 в качестве примера, ниже представлен другой способ визуализировать это:
| 2 n | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Экземпляры в пределах 18 | 1 | 1 0 | 0 | 1 | 0 |
| Цель: 18 | 18-16 = 2 | → | 2-2 = 0 | ||
Преобразование из двоичной системы в десятичную проще .Определите все значения разряда, где встречается 1, и найдите сумму значений.
Пример: 10111 = (1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (1 × 2 1 ) + (1 × 2 0 ) = 23
Отсюда: 16 + 4 + 2 + 1 = 23.
Сложение двоичных файлов
Двоичное сложение следует тем же правилам, что и сложение в десятичной системе, за исключением того, что вместо переноса 1, когда добавленные значения равны 10, перенос происходит, когда результат сложения равен 2.Обратитесь к примеру ниже для пояснения.
Обратите внимание, что в двоичной системе счисления:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, переносится 1, т. Е. 10
Пример:
| 1 0 | 1 1 | 1 1 | 1 0 | 1 | ||
| + | 1 | 0 | 1 | 1 | 1 | |
| = | 1 | 0 | 0 | 1 | 0 | 0 |
Единственная реальная разница между двоичным и десятичным сложением состоит в том, что значение 2 в двоичная система эквивалентна 10 в десятичной системе.Обратите внимание, что единицы с надстрочным индексом представляют собой перенесенные цифры. Распространенная ошибка, на которую следует обратить внимание при выполнении двоичного сложения, — это случай, когда 1 + 1 = 0 также имеет 1, перенесенную из предыдущего столбца вправо. Тогда значение внизу должно быть 1 из перенесенного на 1, а не 0. Это можно увидеть в третьем столбце справа в приведенном выше примере.
Двоичное вычитание
Подобно двоичному сложению, есть небольшая разница между двоичным и десятичным вычитанием, за исключением тех, которые возникают из-за использования только цифр 0 и 1.Заимствование происходит в любом случае, когда вычитаемое число больше, чем число, из которого оно вычитается. При бинарном вычитании заимствование необходимо только тогда, когда 1 вычитается из 0. Когда это происходит, 0 в столбце заимствования по существу становится «2» (изменение 0-1 на 2-1 = 1), в то время как уменьшение 1 в столбце, из которого заимствуется, на 1. Если следующий столбец также равен 0, заимствование должно происходить из каждого последующего столбца, пока столбец со значением 1 не может быть уменьшен до 0.Обратитесь к примеру ниже для пояснения.
Обратите внимание, что в двоичной системе счисления:
- 0 — 0 = 0
0-1 = 1, заимствовать 1, в результате чего -1 переносится на
1 — 0 = 1
1-1 = 0
EX1:
| -1 1 | 2 0 | 1 | 1 | 1 | ||
| — | 0 | 1 | 1 | 0 | 1 | |
| = | 0 | 1 | 0 | 1 | 0 | |
EX2:
| -1 1 | 2-1 0 | 0 | ||
| — | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Обратите внимание, что отображаемые верхние индексы — это изменения, которые происходят с каждым битом при заимствовании.Столбец заимствования по существу получает 2 от заимствования, а столбец, из которого заимствовано, уменьшается на 1.
Двоичное умножение
Двоичное умножение, возможно, проще, чем его десятичный аналог. Поскольку используются только значения 0 и 1, результаты, которые необходимо добавить, либо те же, что и для первого члена, либо 0. Обратите внимание, что в каждой последующей строке необходимо добавить заполнитель 0, а значение сдвинуть влево, как в десятичном умножении. Сложность двоичного умножения возникает из-за утомительного двоичного сложения, зависящего от количества битов в каждом члене.Обратитесь к примеру ниже для пояснения.
Обратите внимание, что в двоичной системе счисления:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
Пример:
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 0 | 1 | 1 | 1 | ||||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Как видно из приведенного выше примера, процесс двоичного умножения такой же, как и при десятичном умножении.Обратите внимание, что заполнитель 0 написан во второй строке. Обычно заполнитель 0 визуально не присутствует при десятичном умножении. Хотя то же самое можно сделать и в этом примере (с предполагаемым заполнителем 0, а не явным), он включен в этот пример, потому что 0 актуален для любого двоичного калькулятора сложения / вычитания, подобного тому, который представлен на этой странице. Без отображения 0 было бы возможно совершить ошибку, исключив 0 при добавлении двоичных значений, показанных выше.Еще раз обратите внимание, что в двоичной системе любой 0 справа от 1 имеет значение, а любой 0 слева от последней единицы в значении — нет.
EX:
- 1 0 1 0 1 1 0 0
= 0 0 1 0 1 0 1 1 0 0
≠ 1 0 1 0 1 1 0 0 0 0
Бинарный отдел
Процесс двоичного деления аналогичен длинному делению в десятичной системе счисления. Дивиденд по-прежнему делится на делитель таким же образом, с единственной существенной разницей, заключающейся в использовании двоичного, а не десятичного вычитания.Обратите внимание, что хорошее понимание двоичного вычитания важно для проведения двоичного деления. Обратитесь к примеру ниже, а также к разделу двоичного вычитания для пояснения.
Калькулятор и счетчик значащих цифр
Если вы найдете этот калькулятор полезным, поделитесь им с друзьями.
Что такое значащие цифры?
Значимые цифры, или для краткости сигинжи, — это значащие цифры в числе. Часто начальные или конечные нули можно удалить, и число останется таким же точным (например, 004 означает то же, что и 4).)
В нашем калькуляторе также есть счетчик, показывающий количество значащих цифр для любого расчета.
Сколько значащих цифр в …?
Вот несколько примеров расчета значимых цифр:
- 7 имеет 1 значащую цифру (7).
- 73 имеет 2 значащие цифры (7 и 3).
- 100 имеет 1 значащую цифру (1).
- 673 имеет 3 значащие цифры (6, 7 и 3).
- 673,52 имеет 5 значащих цифр (6, 3, 7, 5 и 2).
- 0,0637 имеет 3 значащих цифры (6, 3 и 7).
- 30.00 имеет 4 значащих цифры (3, 0, 0 и 0) и 2 десятичных знака.
- 0,0025 имеет 2 значащих цифры (2 и 5) и 4 десятичных знака.
Как считать значащие цифры
Вот правила, которые вам нужно знать для определения значащих цифр.
Все нижеприведенные цифры являются значащими…
- Любая цифра, отличная от 0, всегда значащая
- 0 имеет значение, когда находится между другими цифрами, например 205 или 3.604 (потому что, очевидно, 205 — это не то же самое, что 25)
- Если есть десятичная точка, то любые завершающие нули являются значащими цифрами (например, 90,7500). На первый взгляд эти конечные нули могут показаться ненужными, но они подтверждают точность числа. 90,75 вполне может быть 90,7511 с округлением до двух знаков после запятой. Таким образом, 90.7500 подтверждает, что он полностью точен до четырех знаков после запятой.
И это незначительные цифры…
- Начальные нули перед ненулевой цифрой не являются значащими цифрами (00200 совпадает с 200, а 007 совпадает с 7, поэтому ведущие нули не имеют значения.Они не уточняют число). Этот принцип может сбивать с толку, но ведущие нули все равно не являются значащими цифрами, даже если они идут после десятичной точки. 0,01 кг винограда — это не то же самое, что 1 кг винограда, поэтому ведущие нули могут показаться значительный. Однако 0,01 кг также можно выразить как 10 г. Это та же ценность. Таким образом, ведущие нули не считаются значащими цифрами; это первая часть, которая важна. Конечно, если ноль находится между двумя значащие цифры (например,грамм. 2.303), то ноль имеет значение, в соответствии с правилом (2), объясненным выше.
- Завершающие нули не имеют значения, если десятичная точка не используется. Если есть десятичная точка, то, согласно правилу (3), объясненному выше, любые завершающие нули считаются значащими цифрами.
Подробнее о том, как вычислять и считать значащие числа, вы можете узнать в нашей статье о правилах для значащих чисел.
Другие математические калькуляторы
Ознакомьтесь с математическими калькуляторами на сайте калькулятора, чтобы получить помощь в преобразовании десятичных дробей в дроби и вычислении дробей.
десятичные дроби
Делить на десятичные дроби немного сложно. В наши дни большинство учителей не возражают, если вы воспользуетесь калькулятором. Но хорошо знать, как сделать это самому, и вам всегда нужно уметь оценивать ответ, чтобы вы могли убедиться, что ответ калькулятора разумный.
Напомним, что в задаче Икс ÷ y знак равно z , также написано
y z Икс
Икс называется дивиденд , y это делитель , а также z это частное .
Шаг 1: Оцените ответ округление . Вы будете использовать эту оценку, чтобы проверить свой ответ позже.
Шаг 2: Если делитель не целое число, переместите десятичный разряд п места справа, чтобы превратить его в целое число. Затем переместите десятичный знак в делимом на такое же количество разрядов вправо (при необходимости добавив несколько дополнительных нулей).
Шаг 3: Делить как обычно.Если делитель не входит равномерно, добавьте нули справа от дивиденда и продолжайте делить, пока не получите 0 остаток или пока не появится повторяющийся узор.
Шаг 4: Поместите десятичную запятую в частное прямо над тем местом, где теперь десятичная запятая в делимом.
Шаг 5: Сравните свой ответ со своей оценкой, чтобы увидеть, является ли он разумным.
Пример:
Делить.
0,45 ÷ 3,6
Шаг 1: Поскольку делитель больше делимого, мы получим ответ меньше, чем 1 . С 0,45 примерно в десять раз меньше 3,6 , мы ожидаем ответа, близкого к 0,1 .
Шаг 2: Делитель не является целым числом, поэтому переместите десятичную запятую на одну позицию вправо, чтобы сделать ее целым числом. Также переместите десятичную запятую в делимом на одну позицию вправо.
36 4.5
Шаг 3: Делите нормально, добавляя дополнительные нули справа от 4.5 когда вы закончите.
36 125 4.500 3 6 _ 90 72 _ 180 180 _ 0
Шаг 4: Поместите десятичную точку в частном непосредственно над десятичной точкой в делимом.
36 0,125 4.500 3 6 _ 90 72 _ 180 180 _ 0
Мы получили 0.125 .
Шаг 5: Сравните с вашей первоначальной оценкой. 0,125 близко к 0,1 , так что у нас все хорошо!
Иногда проще решить задачу десятичного деления с помощью мысленной математики. Это хорошая стратегия, когда вы видите, что, перемещая десятичные точки, вы можете превратить проблему в ту, на которую вы запомнили ответ.
Пример:
Делить.
0,42 ÷ 70
Мы знаем это 42 ÷ 7 знак равно 6 .
Если дивиденд является уменьшился с коэффициентом 10 , то коэффициент также уменьшится в 10 .
42 ÷ 7 знак равно 6 4.2 ÷ 7 знак равно 0.6 0,42 ÷ 7 знак равно 0,06
И если делитель является выросла с коэффициентом 10 , то коэффициент уменьшится в 10 .
0,42 ÷ 70 знак равно 0,006
Итак, ответ 0,006 .
Калькулятор стандартной формы(конвертер): Standard Notation Calc.
Калькулятор стандартной формы используется для преобразования чисел в стандартную форму путем помещения десятичного значения в число. Он преобразует длинное число в легко читаемую стандартную форму.
Это калькулятор записи в стандартной форме, который берет число от пользователя и преобразует его в стандартную форму.
В этом содержании мы объясним, что такое стандартная форма, как использовать наш калькулятор стандартной формы, а также как вычислить стандартную форму.
Как пользоваться калькулятором стандартной формы?
Чтобы использовать этот калькулятор стандартной нотации , выполните следующие действия:
- Введите число в данное поле ввода.
- Нажмите кнопку Рассчитать , чтобы увидеть результат.
- Вы можете сбросить значения с помощью Reset
Этот калькулятор формул стандартной формы мгновенно покажет вам преобразованную стандартную форму данного числа. Вы также можете использовать наш калькулятор экспоненциальной записи и конвертер экспоненциальной записи для вычисления научных обозначений.
Что такое стандартная форма?
Если вам интересно, что такое стандартная форма в математике , , вы попали в нужное место.
Стандартная форма используется для уменьшения трудности чтения очень больших или очень маленьких чисел. Стандартная форма числа — это любое число от 1,0 до 10,0, умноженное на степень 10, например, 1,2 × 10 2
Для демонстрации стандартной формы взгляните на следующие примеры:
Число: 85500000000000
Стандартная форма: 8,55 × 10 13
Номер: 0,000458912
Стандартная форма: 4,58 × 10 -4
Как писать в стандартной форме?
Вы можете использовать наш калькулятор преобразования в стандартную форму для расчета стандартной формы любого числа.Однако мы объясним, как преобразовать число в стандартную форму вручную. Чтобы преобразовать число в стандартную форму, выполните следующие действия:
- Запишите число.
- Определите десятичную точку в числе. Если в данном числе нет десятичной точки, считается, что оно находится справа от числа после последней цифры.
- После определения десятичной точки переместите десятичную дробь на первую ненулевую цифру в числе.
4.Подсчитайте общее количество цифр, на которое вы переместили десятичную точку. Умножьте это число на 10 и увеличьте степень 10 с общим количеством перемещенных десятичных цифр. Если десятичная дробь перемещается справа налево, степень будет положительной, а если десятичная дробь перемещается слева направо, степень будет отрицательной.
Пример:
Преобразование 0,0009 в стандартную форму.
Решение:
Следуйте инструкциям, чтобы найти стандартную форму данного числа.
Шаг 1 : Запишите номер.
0,0009
Шаг 2 : Определите десятичную точку в числе. Вы можете видеть, что десятичная точка находится после 4 цифр слева.
Шаг 3 : После определения десятичной точки переместите десятичную дробь на первую ненулевую цифру числа .
Это превратится в 9. Поскольку после 9 нет ненулевой цифры, нам не нужно записывать десятичную точку после 9.
Шаг 4 : Подсчитайте общее количество цифр, на которое вы переместили десятичную точку. Мы переместили десятичную запятую на 4 позиции дальше. Умножьте это число на 10 и увеличьте степень 10 с общим количеством перемещенных десятичных цифр. Поскольку мы переместили десятичную точку слева направо, степень будет отрицательной.
9 × 10 -4
Итак, стандартная форма числа 0,0009 — 9 × 10 -4 . 4 Стандартное приложение «Калькулятор» на iPhone в последнее время получило немало прессы из-за своего жеста «проведите пальцем для удаления», но оно давно стало рабочей лошадкой на iPhone — фактически, оно существует с момента запуска самой первой модели Apple в 2007 году. С годами внешний вид калькулятора несколько изменился, но его основные функции остались прежними: помочь вам быстро складывать, вычитать и возводить в квадрат суммы и числа. Вот как вы можете использовать некоторые из основных функций приложения «Калькулятор» и некоторые из его скрытых жемчужин. Вы можете получить доступ к приложению «Калькулятор» на iPhone четырьмя способами: с помощью значка приложения «Калькулятор», Siri, панели поиска или Центра управления. Для всего, от ремонта и улучшения дома до разделения счета за обед, вы можете перейти к калькулятору одним касанием. VPN-предложения: пожизненная лицензия за 16 долларов, ежемесячные планы за 1 доллар и более Нажмите кнопку Calculator внизу, вторая справа. Интересный факт: вы также можете сильно нажать (3D Touch, iPhone 6s или новее) на значок калькулятора, если хотите скопировать последний расчет из приложения. Чтобы запустить приложение «Калькулятор» с главного экрана, вы можете выполнить одно из трех действий: Когда вы впервые открываете приложение «Калькулятор», вам предоставляется базовый интерфейс калькулятора: виртуальная клавиатура с 10 цифрами (0–9) с элементами управления десятичными знаками, очисткой уравнения, добавлением положительности или отрицательности к числу, поворотом числа на процент, деление, умножение, вычитание, сложение и вычисление уравнения. Случайно набрал 8, когда хотел нажать 9? Это легко исправить. Примечание. Это работает только для цифровой клавиатуры (0-9) и кнопки десятичной точки; если вы случайно нажмете любую из кнопок математических операций, вы не сможете использовать этот жест. Если вы ошиблись, проведите по экрану влево на черном дисплее, чтобы стереть самое последнее число или десятичную точку. Введите свой второй номер. Нажмите кнопку Рассчитать. Это число и есть сумма ваших чаевых. Приложение «Калькулятор» также имеет несколько скрытый режим научного калькулятора. Чтобы получить к нему доступ, поверните свой iPhone из портретного в альбомный режим; пока кнопка Rotation Lock отключена, экран калькулятора должен сместиться в альбомную ориентацию с новыми кнопками для квадратных корней, экспоненциальных уравнений, логарифмических уравнений, тригонометрии и т. д. Спойлер: Я не собираюсь объяснять, как использовать научный калькулятор для вычисления конкретных уравнений. Если вы хотите узнать больше о сложных математических уравнениях, я предлагаю посетить Академию Хана или вашу местную библиотеку, или написать по электронной почте вашим старым учителям математики. Встроенное приложение «Калькулятор» для iPhone довольно хорошо с точки зрения основ, но если вы ищете подробные варианты, которые предоставят вам сохраненные прошлые уравнения, подготовку налогов, конвертацию валюты и многое другое, вам может потребоваться стороннее приложение. Есть вопросы о приложении «Калькулятор»? Дайте нам знать об этом в комментариях. Как использовать приложение «Калькулятор» на iPhone
Как запустить приложение «Калькулятор»
Как запустить приложение «Калькулятор» из Центра управления
Как запустить приложение «Калькулятор» с главного экрана, Siri или панели поиска
Как пользоваться приложением «Калькулятор»
Как отменить ошибочное число
Как складывать, вычитать, умножать или делить в приложении «Калькулятор»
Как рассчитать чаевые в приложении «Калькулятор»
Как пользоваться научным калькулятором
Альтернативные варианты калькулятора
Вопросы?


 В конце урока мы посмотрим, у какой команды букет получился более пышным.
В конце урока мы посмотрим, у какой команды букет получился более пышным.





 задач»
задач» ру:
ру: ру:
ру: