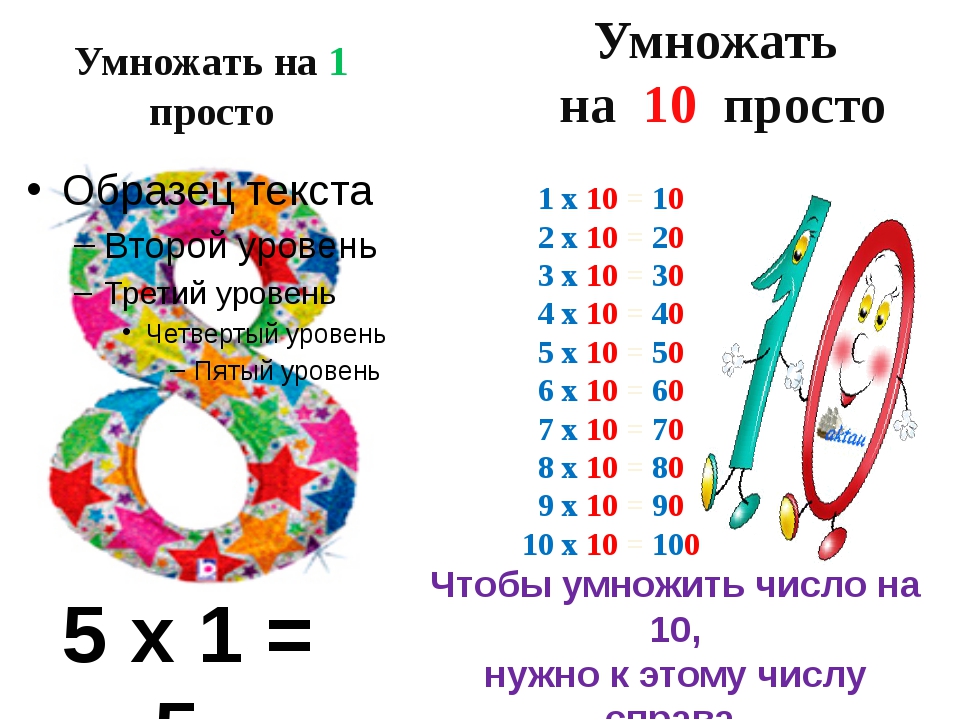
Умножение на пальцах (на 6, 7, 8, 10) | МатЬиматика
Как помочь ребёнку быстро и легко запомнить таблицу умножения? Используйте «пальцулятор».
1. Держите руки так, чтобы ладони были повернуты к телу, а пальцы располагались друг напротив друга. Каждый палец снова будет соответствовать числу. Мизинцы соответствуют числу шесть, безымянные пальцы – числу семь, средние пальцы – числу восемь, указательные пальцы – числу девять, а большие пальцы соответствуют числу десять.
2. Соприкоснитесь пальцами, которые соответствуют нужным числам. Например, чтобы решить пример 7×6, коснитесь левым безымянным пальцем правого мизинца. Пальцы левой руки будут соответствовать числу с левой стороны от знака умножения, а пальцы правой руки – числу с правой стороны от знака умножения. Не забывайте, что каждый палец соответствует своему числу, а в данном примере безымянный палец соответствует числу семь, а мизинец – числу шесть. Следовательно, вам нужно соприкоснуться этими пальцами, чтобы решить данный пример.
Возможно, что вам потребуется неудобно выгнуть кисть!
Еще один пример: если вам нужно умножить 9×7, то коснитесь левым указательным пальцем правого безымянного пальца.
3. Сложите пальцы, которые соприкасаются, а также пальцы под ними. Теперь вам нужно посчитать соприкасающиеся пальцы и те пальцы, что находятся ниже. Они соответствуют десяткам. В нашем примере считаем безымянный палец на левой руке, мизинец на левой руке и мизинец на правой руке. Каждый из пальцев учитывается как число 10. В нашем случае получаем сумму 30.
4. Умножьте оставшиеся пальцы. Далее сложите число пальцев на каждой руке, за исключением соприкасающихся пальцев. Сначала подсчитайте количество пальцев на левой руке, которые находятся выше соприкасающихся пальцев – в данном случае это 3. Затем сосчитайте количество пальцев на правой руке выше соприкасающихся пальцев – в данном случае это 4. 3×4 = 12.
5. Сложите два числа вместе, чтобы узнать ответ. В данном примере необходимо сложить 30 и 12, чтобы в итоге получить 42.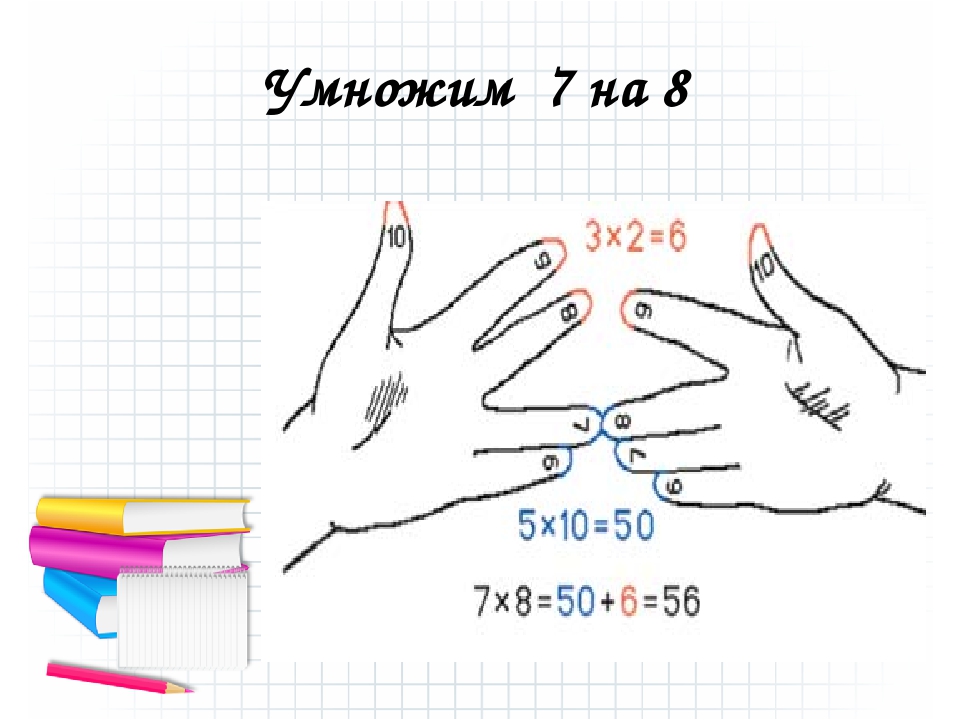 Правильно, 7×6 = 42!
Правильно, 7×6 = 42!
6. Умножайте на 10, используя такой же способ. Например, если вы хотите решить пример 10×7, то сначала прикоснитесь левым большим пальцем к правому безымянному пальцу. Подсчитайте количество пальцев ниже соприкасающихся пальцев, включая соприкасающиеся пальцы. У вас получится сумма 7, что соответствует числу 70. Затем сосчитайте количество пальцев выше соприкасающихся пальцев на правой и левой руке. У вас получится 0 слева и 3 справа. Теперь умножьте 3×0, что равно 0, а для получения ответа сложите 70 и 0. Правильно, 10×7 = 70!
7. Используйте этот способ, чтобы умножать на шесть, семь, восемь и десять. Как умножить 8 на 8 с помощью пальцев? А как насчет 7 на 10?
Таблица умножения на 6, 7, 8, 9. Математика, 3 класс: уроки, тесты, задания.
Вход Вход Регистрация Начало Новости ТОПы Учебные заведения Предметы Проверочные работы Обновления Переменка Поиск по сайту Отправить отзыв-
Умножение на 6 (таблица)
-
Умножение на 7 (таблица)
-
Умножение на 8 (таблица)
-
Умножение на 9 (таблица)
никакого гадания, только теория чисел / Хабр
В данной статье речь пойдёт о таких понятиях теории чисел, как цифровой корень и ведический квадрат.
Данная статья ничего не говорит о нумерологии, кроме того, что это псевдонаучная концепция.
Цель данной статьи: показать математические закономерности вокруг вычисления цифрового корня и его связь с циклическими числами.
Введение
Несколько дней назад я решил написать незатейливую статью про нумерологическое сложение. Моей целью было показать, что даже такая незамысловатая операция может иметь большое количество интересных закономерностей. Многие из этих закономерностей я нашёл ещё в школьное время, когда скучал на уроках географии. При внимательном рассмотрении я нашёл больше закономерностей, чем ожидал, и это привело меня назад к моей любимой теме full reptend prime.
После я внимательно изучил то, что нашёл, узнал, что многие из этих понятий уже существуют, и решил переписать статью заново, чтобы опираться на общеизвестные понятия. Помимо известных понятий я добавил собственные визуализации, чтобы сделать чтение немного более увлекательным.
Сумма цифр и цифровой корень
 Операция выполняется до тех пор, пока вычисленное значение не становится меньше заданной системы счисления, т.е. до тех пор, пока оно не равняется одной-единственной цифре.
Операция выполняется до тех пор, пока вычисленное значение не становится меньше заданной системы счисления, т.е. до тех пор, пока оно не равняется одной-единственной цифре. Аддитивная стойкость натурального числа — это количество итераций, на которых нужно применить операцию суммы цифр, для того чтобы получить цифровой корень.
Пример: Цифровая сумма числа 142857 равна 1 + 4 + 2 + 8 + 5 + 7 = 27
Цифровая сумма числа 27 равна 2 + 7 = 9
Как следствие, цифровой корень числа 142857 = 9, аддитивная стойкость 142857 = 2.
Код для вычисления цифрового корня в произвольной системе счисления на языке Python:
def digitalRootRecurrent(number, base):
digitSum = 0
while number > 0:
digitSum += number % base
number //= base
if digitSum >= base:
digitSum = digitalRootRecurrent(digitSum, base)
return digitSumПрименение цифровой суммы
Цифровые суммы применялись при расчёте контрольных сумм для проверки арифметических операций ранних компьютеров. Ранее, в эпоху ручного счета, Фрэнсис Исидор Эджуорт предложил использовать суммы 50 цифр, взятых из математических таблиц логарифмов, в качестве формы генерации случайных чисел; если предположить, что каждая цифра случайна, то по центральной предельной теореме эти цифровые суммы будут иметь случайное распределение, близкое к гауссову распределению.
Ранее, в эпоху ручного счета, Фрэнсис Исидор Эджуорт предложил использовать суммы 50 цифр, взятых из математических таблиц логарифмов, в качестве формы генерации случайных чисел; если предположить, что каждая цифра случайна, то по центральной предельной теореме эти цифровые суммы будут иметь случайное распределение, близкое к гауссову распределению.
Цифровая сумма двоичного представления числа известна как вес Хэмминга или численность населения. Алгоритмы выполнения этой операции были изучены, и она была включена в качестве встроенной операции в некоторые компьютерные архитектуры и некоторые языки программирования. Эти операции используются в вычислительных приложениях, включая криптографию, теорию кодирования и компьютерные шахматы.
Улучшение алгоритма вычисления цифрового корня
При расчёте цифрового корня можно воспользоваться небольшой хитростью: если значение не равно нулю, и не равно основанию системы счисления — 1, можно получить значение цифрового корня просто операцией взятия остатка от деления на основание системы счисления — 1.
Модифицированный код:
def digitalRoot(number, base):
if number == 0:
return 0
dR = number % (base - 1)
if dR == 0:
dR = base - 1
return dRСвойства цифрового корня
Операция сложения
Сделаем небольшую таблицу, для того чтобы изучить закономерности, каким образом вычисляется цифровой корень суммы двух чисел:
Таблица для анализа операции цифрового корня суммы двух чисел.Код для построения таблицы суммы:
firstTermRangeStart = 2
firstTermRangeEnd = 8
secondTermRangeStart = 1
secondTermRangeEnd = 9
base = 10
for j in range(firstTermRangeStart, firstTermRangeEnd + 1):
print()
for i in range(secondTermRangeStart, secondTermRangeEnd + 1):
if i % (secondTermRangeEnd + 1) == 0:
print()
print('dr(',j,'+', i, ') =', digitalRoot(j + i, base), ' ', end='')Как можно увидеть, цифровой корень суммы чисел равен цифровому корню суммы цифровых корней этих чисел:
Операция вычитания
Формула похожа на предыдущую, однако совпадает не полностью.
Приведем контрпример: 455 — 123 = 332.
Как можно отметить, выражение 4 — 6 не даёт в результате 8, потому формулу сложения нужно модифицировать, чтобы она работала для операции вычитания:
Операция умножения
Выведем вариацию таблицы умножения, для того чтобы исследовать эту операцию:
Расчет цифрового корня от двух множителейКод для вывода таблицы умножения:
firstTermRangeStart = 1
firstTermRangeEnd = 8
secondTermRangeStart = 1
secondTermRangeEnd = 9
base = 10
for i in range(secondTermRangeStart, secondTermRangeEnd + 1):
print()
for j in range(firstTermRangeStart, firstTermRangeEnd + 1):
print('dr(',j,'*', i, ') =', digitalRoot(i * j, base), ' ', end='') Запишем значения для каждого множителя:
1) [1, 2, 3, 4, 5, 6, 7, 8, 9]
2) [2, 4, 6, 8, 1, 3, 5, 7, 9]
3) [3, 6, 9, 3, 6, 9, 3, 6, 9]
4) [4, 8, 3, 7, 2, 6, 1, 5, 9]
5) [5, 1, 6, 2, 7, 3, 8, 4, 9]
6) [6, 3, 9, 6, 3, 9, 6, 3, 9]
7) [7, 5, 3, 1, 8, 6, 4, 2, 9]
8) [8, 7, 6, 5, 4, 3, 2, 1, 9]
9) [9, 9, 9, 9, 9, 9, 9, 9, 9]
Можно увидеть, что последовательности разбиваются на пары 1 и 8, 2 и 7, 3 и 6, 4 и 5.
Также отметим, что при умножении на основание системы счисления -1 цифровой корень будет равен основанию системы счисления — 1. При умножении на 1 значение цифрового корня второго множителя сохраняется.
Визуализация последовательностей:
Последовательности для множителей 1, 2, 3, 4. Они же являются зеркальными для 8, 7, 6, 5.Последовательности можно рассмотреть как множество всех возможных замкнутых фигур с количеством точек, равным основанию системы счисления — 1, начиная с правильного n-угольника. Исключением является множитель, который не является взаимно простым с основанием системы счисления — 1, в данном случае это 3 и 6.
Для нахождения последовательности любой линии можно записать формулу:
Если записать эти значения как множество пересечений всех множителей, мы получим в результате ведический квадрат.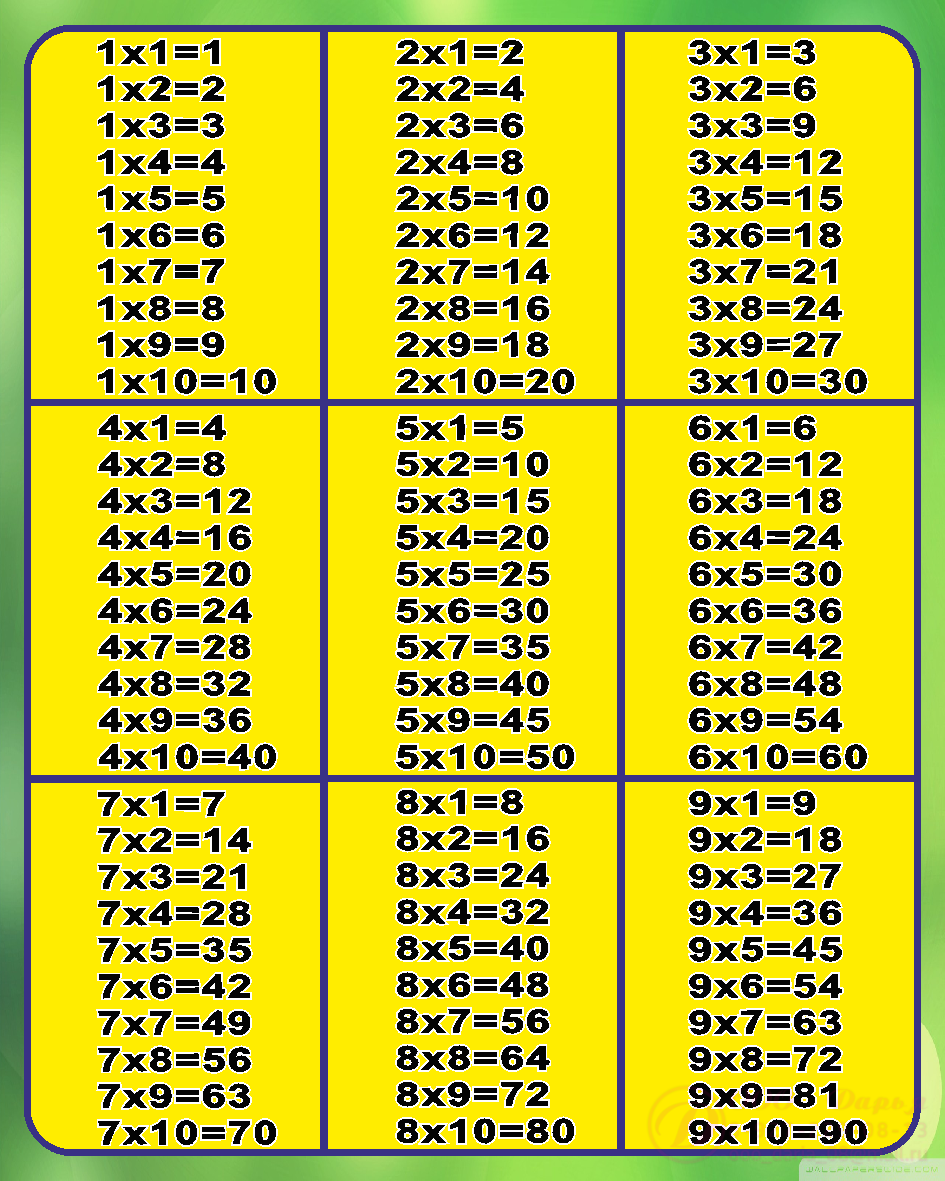
Подмножество данного ведического квадрата формирует собой латинский квадрат. Чтобы получить его, нужно вычеркнуть элементы, равные основанию системы счисления — 1.
Приведение ведического квадрата к латинскому квадрату в десятичной системе счисления.В результате мы получим:
Подмножество ведического квадрата, составляющее латинский квадрат в десятичной системе счисления.Если переставить некоторые из его строчек местами, мы получим последовательность циклических чисел. О том, каким образом должны быть осуществлены перестановки строчек, будет рассказано ниже при исследовании других операций с цифровым корнем.
Ниже приведена ещё одна картинка ведических квадратов для систем счисления 100 и 1000. Белым отмечены самые большие значения клеток — соответствующие основанию системы счисления — 1, черным — самые маленькие, соответствующие 1.
Теперь вернемся к произведению. Цифровой корень произведения одиночных цифр в заданной системе счисления вычисляется при помощи соответствующего ведического квадрата.
Цифровой корень произведения одиночных цифр в заданной системе счисления вычисляется при помощи соответствующего ведического квадрата.
Для вычисления цифрового корня произведения двух чисел, которые содержат больше одной цифры, для начала нужно вычислить цифровой корень каждой из этих цифр, и после этого воспользоваться ведической площадью.
Операция деления
Рассмотрим те числа, которые дают при делении непериодические дроби, это 2, 5, 4, 8.
Для того чтобы быть уверенными, что мы не допускаем ошибок, воспользуемся уже выведенными правилами и умножим результат деления на 1000; так как цифровой корень 1000 равен 1, то произведение будет иметь тот же самый цифровой корень.
Таблица деления для делителей, которые взаимно просты с десятичной системой счисления.base = 10
divisors = [2, 4, 5, 8]
for j in divisors:
print()
for i in range(1, base):
value = (digitalRoot(int((i / j) * (base ** 3)), base))
print('dr(',i, '/', j, ') =', value, ' ', end='') Тут бросаются в глаза несколько закономерностей. Число 9 не только при умножении, но и при делении приводит к значению цифрового корня, равному 9. Интересное происходит также с числами 3 и 6, эти числа как при умножении, так и при делении дают абсолютно одинаковые значения цифрового корня.
Число 9 не только при умножении, но и при делении приводит к значению цифрового корня, равному 9. Интересное происходит также с числами 3 и 6, эти числа как при умножении, так и при делении дают абсолютно одинаковые значения цифрового корня.
Запишем в таблицу череду делений:
2) [5, 1, 6, 2, 7, 3, 8, 4, 9] — Эта последовательность встречалась в множителе 5
4) [7, 5, 3, 1, 8, 6, 4, 2, 9] — Эта последовательность встречалась в множителе 7
5) [2, 4, 6, 8, 1, 3, 5, 7, 9] — Эта последовательность встречалась в множителе 2
8) [8, 7, 6, 5, 4, 3, 2, 1, 9] — Эта последовательность встречалась в множителе 8
Операция деления для цифрового корня определена только для делителей, которые не являются взаимно простыми с основанием системы счисления.
Операция возведения в степень
Таблица возведения в степень:
Таблица возведения в степень в десятичной системе счисления.base = 10
.
for i in range(2, base - 2):
print()
for j in range(1, base - 1):
print('dr(', j ,'^', i, ') =', digitalRoot(i ** j, base), ' ', end='') Здесь мы можем наблюдать цикличность. n + 1, где p — это простое число, а n — натуральное.
n + 1, где p — это простое число, а n — натуральное.
Рассмотрим систему счисления 8, череда его значений будет равна [1, 3, 2, 6, 4, 5]. Именно такие же остатки от деления мы получаем при делении числа в десятичной системе счисления.
Деление 1 на 7 в столбик. Здесь мы можем наблюдать остатки от деления [1, 3, 2, 6, 4, 5]. Последовательность полученная при возведении в степень, в восьмеричной системе счисления.Это свойство связано с тем, что вычисление цифрового корня можно осуществить при помощи альтернативной формулы расчета цифрового корня:
Ещё визуализации
Приведём ниже визуализации для операции возведения в степень для разных систем счисления, все они будут связанны с паттернами, образующимися в рациональных дробях 1/P, где P — это full reptend prime.
Остатки от деления, найденные в 6 системе счисления, связанные с числом 5.Остатки от деления, найденные в 10 системе счисления, связанные с квадратом числа 3.Остатки от деления, найденные в 12 системе счисления, связанные с числом 11. Остатки от деления, найденные в 14 системе счисления, связанные с числом 13.Остатки от деления, найденные в 18 системе счисления, связанные с числом 17.Остатки от деления, найденные в 20 системе счисления, связанные с числом 19.Остатки от деления, найденные в 26 системе счисления, связанные с квадратом числа 5.Остатки от деления, найденные в 28 системе счисления, связанные с кубом числа 3.
Остатки от деления, найденные в 14 системе счисления, связанные с числом 13.Остатки от деления, найденные в 18 системе счисления, связанные с числом 17.Остатки от деления, найденные в 20 системе счисления, связанные с числом 19.Остатки от деления, найденные в 26 системе счисления, связанные с квадратом числа 5.Остатки от деления, найденные в 28 системе счисления, связанные с кубом числа 3.Теперь приведём несколько картинок из ведических квадратов, принцип их формирования очень прост, потому ограничимся небольшим количеством:
Замкнутая фигура из 6 системы счисления, связана с числом 5.Замкнутые фигуры из 8 системы счисления, связанные с числом 7.Замкнутые фигуры из 12 системы счисления, связанные с числом 11.Образование циклических чисел при помощи ведической площади и остатков от деления
После того как мы получили латинский квадрат из ведического квадрата, пронумеруем его строки последовательно:
Пронумерованный латинский квадрат.Теперь мы можем переставить строки на основании череды остатков от деления, таким образом мы получим последовательность циклических чисел.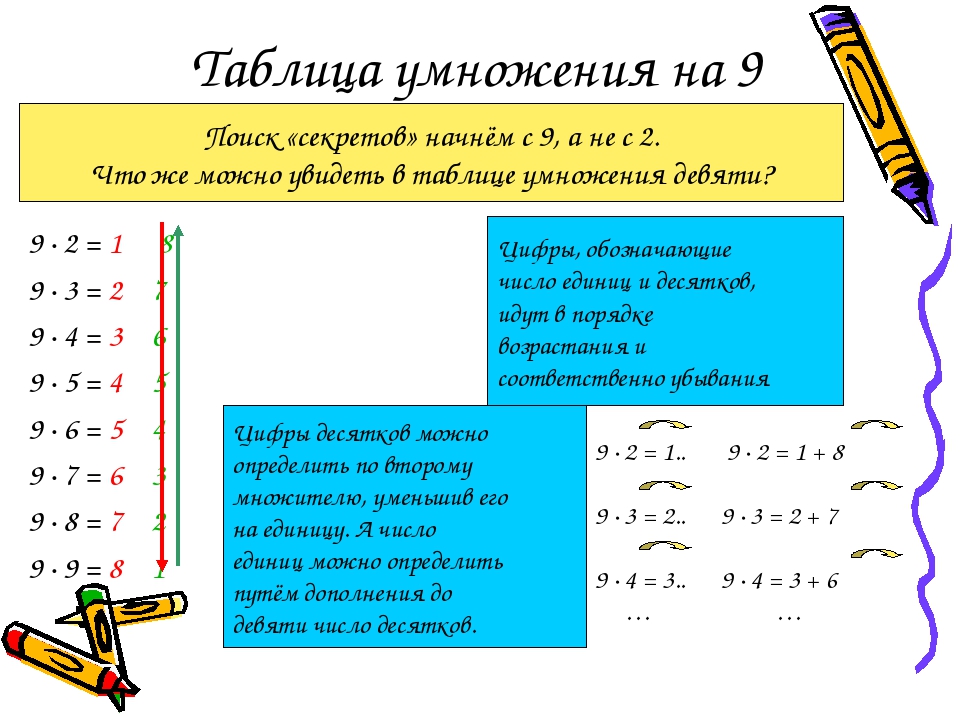 Напомню, остатки от деления были равны [1, 3, 2, 6, 4, 5]. В результате у нас получится следующая картина:
Напомню, остатки от деления были равны [1, 3, 2, 6, 4, 5]. В результате у нас получится следующая картина:
Как можно наблюдать, первый столбец теперь представляет собой циклическое число 142857.
Выводы
Несмотря на плохую репутацию нумерологии, операции суммы цифр и цифрового корня имеют пусть не широкое, но всё же практическое применение.
Например, с помощью цифрового корня можно сформировать множество замкнутых n-вершинных звезд, многие из которых очень любят современные рок\метал группы 🙂
Пентаграмма — в представлении не нуждается 🙂 Уроборос тут не случайно, о нем в следующей статье!Tool предпочитают 8 систему счисления, связанную с простым числом 7.Slipknot тяготеют к десятеричной системе счисления, связанной с квадратом числа 3.Как можно видеть, многие метал группы тоже любят теорию чисел!
Но лично я для своей метал группы решил выбрать анимированный логотип, составленный из одновременной визуализации периодических дробей, образованных из 90 рациональных дробей 1/91. .90/91:
.90/91:
Если у кого-то есть дополнительная информация об описанных выше понятиях, пожалуйста присылайте её в комментарии, я буду очень благодарен!
Надеюсь, что вам было интересно, большое спасибо за внимание!
Intel представила восьмиядерные Tiger Lake-H — лучшие мобильные процессоры для геймеров
Компания Intel расширила семейство мобильных процессоров Core 11-го поколения, добавив в него новых представителей H-серии, рассчитанных на применение в мощных игровых и рабочих ноутбуках. В число новинок входят 10 моделей CPU, известных ранее под кодовым именем Tiger Lake-H, — они имеют до восьми вычислительных ядер, увеличенное число линий PCIe 4.0 и высокие тактовые частоты, которые доходят до 5,0 ГГц у флагмана.
Сегодняшним анонсом Intel существенно поднимает планку производительности мобильных систем. Новые модели процессоров Core 11-го поколения используют микроархитектуру Willow Cove с показателем IPC на 19 % выше, чем у предшественников, и производятся по современному техпроцессу Intel SuperFin с нормами 10 нм. При этом их отличие от вышедших ранее представителей семейства Tiger Lake заключается в том, что они предлагают пользователям удвоенное до восьми количество вычислительных ядер, работающих на относительно высоких частотах. Это позволяет применять такие процессоры как в высокопроизводительных игровых ноутбуках, так и в мобильных рабочих станциях.
При этом их отличие от вышедших ранее представителей семейства Tiger Lake заключается в том, что они предлагают пользователям удвоенное до восьми количество вычислительных ядер, работающих на относительно высоких частотах. Это позволяет применять такие процессоры как в высокопроизводительных игровых ноутбуках, так и в мобильных рабочих станциях.
Полупроводниковый кристалл Tiger Lake-H
Старшая модель в новом семействе представлена восьмиядерным процессором Core i9-11980HK, имеющим максимальную частоту в турборежиме 5,0 ГГц и максимально допустимую частоту при нагрузке на все ядра 4,5 ГГц. Кроме того, этот процессор, несмотря на мобильное предназначение, поддерживает разгон: он позволяет менять коэффициенты умножения и напряжения. Помимо Core i9-11980HK, в семейство входят восьмиядерники Core i9-11900H (максимальная частота 4,9 ГГц) и Core i7-11800H (частота до 4,6 ГГц), а также шестиядерники Core i5-11400H (частота до 4,5 ГГц) и Core i5-11260H (до 4,4 ГГц).
Увеличение в Tiger Lake-H числа вычислительных ядер потребовало от производителя урезать интегрированное графическое ядро Intel Xe. Оно в новых CPU располагает лишь 32 исполнительными устройствами, и поэтому графика в Tiger Lake-H относится к классу UHD Graphics, а не Iris Xe. Но её возможностей достаточно как для аппаратного ускорения кодирования/декодирования видео, так и для работы с алгоритмами машинного обучения.
Оно в новых CPU располагает лишь 32 исполнительными устройствами, и поэтому графика в Tiger Lake-H относится к классу UHD Graphics, а не Iris Xe. Но её возможностей достаточно как для аппаратного ускорения кодирования/декодирования видео, так и для работы с алгоритмами машинного обучения.
Зато в Tiger Lake-H появилась поддержка 20 линий PCIe 4.0 на стороне процессора — подобно десктопным Rocket Lake. Это позволяет устанавливать в ноутбуки на базе новых процессоров высокопроизводительную мобильную графику серии GeForce RTX 3000 и быстрейшие потребительские SSD. Также конфигурация мобильных систем на базе Tiger Lake-H может включать память вплоть до DDR4-3200, порты Thunderbolt 4 со скоростью до 40 Гбит/с и Wi-Fi 6E.
Сама Intel говорит о процессорах Tiger Lake-H не иначе как о самых быстрых CPU для игровых ноутбуков. По данным компании, Core i9-11980HK превосходит Core i9-10980HK поколения Comet Lake-H в играх (в аналогичной конфигурации с графикой GeForce RTX 3080) в среднем на 12 %.
Более того, преимущество Core i9-11980HK над субфлагманским мобильным процессором конкурента, Ryzen 9 5900HX, достигает в среднем 19 % (с графикой GeForce RTX 3080).
Помимо перечисленных моделей процессоров Core 11-го поколения Intel также представила три мобильные модификации vPro, ориентированные на бизнес-применения: восьмиядерные Core i9-11950H и Core i7-11850H, а также шестиядерную — Core i5-11500H. Это процессоры отличаются поддержкой набора технологий vPro и Trusted Execution Technology, а также являются частью программы Intel SIPP. И наконец, в семействе Tiger Lake-H выпущено два мобильных профессиональных процессора Xeon W-11955M и Xeon W-11855M с восемью и шестью ядрами соответственно, поддерживающие ко всему прочему память с ECC.
Предполагается, что старшие модели новых Tiger Lake-H найдут применение в ноутбуках верхнего уровня с 15-17-дюймовым дисплеем с высокой частотой обновления, а также с толщиной корпуса менее 20 мм. Такие компьютеры, оснащённые дискретными видеоускорителями последнего поколения, должны «потянуть» средние и даже высокие настройки качества в играх в разрешении 4K. Кроме того, средние модели Tiger Lake-H могут попадать и в более простые мобильные компьютеры, рассчитанные на гейминг в разрешении 1080p. Intel обещает, что на базе новых Tiger Lake-H в течение года будет выпущено до 80 различных дизайнов ноутбуков, а более миллиона 10-нм восьмиядерных мобильных чипов уже отгружено партнёрам. Таким образом, продажи мобильных систем с восьмиядерными Intel Core 11-го поколения начнутся в самое ближайшее время.
Кроме того, средние модели Tiger Lake-H могут попадать и в более простые мобильные компьютеры, рассчитанные на гейминг в разрешении 1080p. Intel обещает, что на базе новых Tiger Lake-H в течение года будет выпущено до 80 различных дизайнов ноутбуков, а более миллиона 10-нм восьмиядерных мобильных чипов уже отгружено партнёрам. Таким образом, продажи мобильных систем с восьмиядерными Intel Core 11-го поколения начнутся в самое ближайшее время.
Если вы заметили ошибку — выделите ее мышью и нажмите CTRL+ENTER.
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т. е.е., для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
е.е., для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью. Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, т. Е. 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной запятой . , и они автоматически конвертируются в дроби — то есть 1,45 .
Двоеточие : и косая черта / являются символом деления. Может использоваться для деления смешанных чисел 1 2/3: 4 3/8 или может использоваться для записи сложных дробей i. 1/2
1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное дробное: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам для порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Дроби в задачах со словами:
следующие математические задачи »
Таблица 7 раз — Математика с мамой
Что такое 7-кратная таблица?
Таблица умножения семерок составлена путем суммирования семерок.
- 1 × 7 = 7
- 2 × 7 = 14.
- 3 × 7 = 21
- 4 × 7 = 28
- 5 × 7 = 35
- 6 × 7 = 42
- 7 × 7 = 49
- 8 × 7 = 56
- 9 × 7 = 63
- 10 × 7 = 70
- 11 × 7 = 77
- 12 × 7 = 84
Таблица умножения на 7 обычно считается одной из самых сложных для запоминания таблиц умножения.
При обучении таблице умножения на 7 полезно уже запомнить другие таблицы умножения, чтобы их можно было использовать для изучения этой.
Рекомендуется, чтобы таблица умножения на 7 умножалась последней из всех таблиц умножения. Однако это не означает, что другие таблицы умножения должны быть идеальными, прежде чем их можно будет представить. Совместное использование всех таблиц умножения может помочь укрепить их.
Как запомнить 7-кратную таблицу
Чтобы запомнить таблицу умножения на 7, начните с изучения 1 × 7 = 7, 10 × 7 = 70 и 11 × 7 = 77.Эти ответы находятся в других таблицах умножения, которые легче всего запомнить. Затем мы можем вспомнить 2 × 7 = 14, удвоив 7, и 4 × 7 = 28, снова удвоив этот ответ.
Есть уловка, чтобы запомнить 3, 6, 9 и 12 умножить на 7, то есть цифры в этих ответах в сумме дают 3, 6, 9 и 12.
Наконец, выучите 5, 7 и 8 раз 7. Мы можем помнить, что 5 × 7 = 35 — единственный ответ, который заканчивается на 5, 8 × 7 = 56 содержит цифры 5, 6, 7 и 8. 7 × 7 = 49 можно найти, прибавив 7 к 6 × 7 = 42.
Теперь мы рассмотрим некоторые из этих приемов с таблицей умножения на 7 более подробно.
Мы рассмотрим таблицу 7 умножений в том порядке, в котором их лучше всего выучить.
Вот самые простые ответы в таблице умножения на семь.
1 × 7 = 7, потому что умножение числа на 1 не меняет числа.
Умножение 7 на 1 равно 7.
Следующее простое умножение из таблицы умножения на 7: 10 × 7 = 70.
Помните, что для умножения цифры на 10 мы просто ставим ноль в конце цифры.
Мы ставим 0 в конце после 7, чтобы получить 70. 10 × 7 = 70.
Умножить одну цифру на 11 легко, потому что мы просто повторяем цифру.
11 × 7 = 77. Мы просто повторяем 7, так что оно написано дважды.
После изучения 1 × 7 = 7, 10 × 7 = 70 и 11 × 7 = 77, следующие самые простые для изучения — это 2 × 7 и 4 × 7.
Умножение на 2 означает удвоение числа. Удвоить легко, потому что мы просто добавляем число к самому себе.
7 + 7 = 14 и, значит, 2 × 7 = 14.
4 × 7 в два раза больше, чем 2 × 7.
Это означает, что мы можем найти ответ на 4 × 7, удвоив ответ до 2 × 7.
14 + 14 = 28 и, следовательно, 4 × 7 = 28.
Следующее простое умножение, которое нужно запомнить в таблице умножения на 7, — это числа, кратные 3. Это потому, что у нас есть трюк с таблицей умножения на 7 для этих чисел.
У нас есть:
3 × 7 = 21
6 × 7 = 42
9 × 7 = 63
12 × 7 = 84
Мы можем запомнить эти ответы, потому что цифры в каждом ответе добавляют к числу, которое мы умножили на 7.
3 × 7 = 21 и 2 + 1 = 3
6 × 7 = 42 и 4 + 2 = 6
9 × 7 = 63 и 6 + 3 = 9
12 × 7 = 84 и 8 + 4 = 12
Вот 3 × 7 = 21.
Вот 6 × 7 = 42.
Вот 9 × 7 = 63.
Вот 12 × 7 = 84.
Мы также можем вычислить 12 × 7, умножив 7 на 10 и на 2, а затем сложив два результата вместе.
10 × 7 = 70 и 2 × 7 = 14.
70 + 14 = 84 и, значит, 12 × 7 = 84.
Есть еще 3 таблицы умножения, которые нужно выучить в таблице умножения на 7.
5 × 7 = 35 — следующее простое для изучения число, потому что это единственное число в таблице умножения на 7, которое заканчивается на 5.
Мы можем легко умножить число на 5, умножив его на 10 и разделив пополам.
10 × 7 = 70, а половина 7 — 35.
Следующее, что легче всего запомнить, — это 8 × 7 = 56.
Мы можем помнить это, потому что вопрос и ответ содержат цифры 5, 6, 7 и 8.
Мы просто должны помнить, что цифры 5, 6, 7 и 8 находятся в неправильном порядке при умножении.
Наконец, самая сложная таблица умножения, которую нужно запомнить, — это 7 × 7 = 49.
Поскольку таблица умножения на 7 является одной из самых сложных для запоминания, 7 × 7 = 49 часто запоминается наименее хорошо из всех таблиц умножения.
Лучший способ вычислить 7 × 7 = 49 — это запомнить 6 × 7 = 42 и просто добавить к этому еще 7.
2 + 7 = 9 и поэтому 42 + 7 = 49.
При обучении таблице умножения на 7 рекомендуется часто пересматривать 7 × 7 = 49 и 8 × 7 = 56. Поскольку для этих двух таблиц умножения не так много уловок с таблицей быстрого умножения, лучше всего изучить эти две таблицы с помощью повторение и умножение настольных игр, пока вы не научитесь бегло говорить.
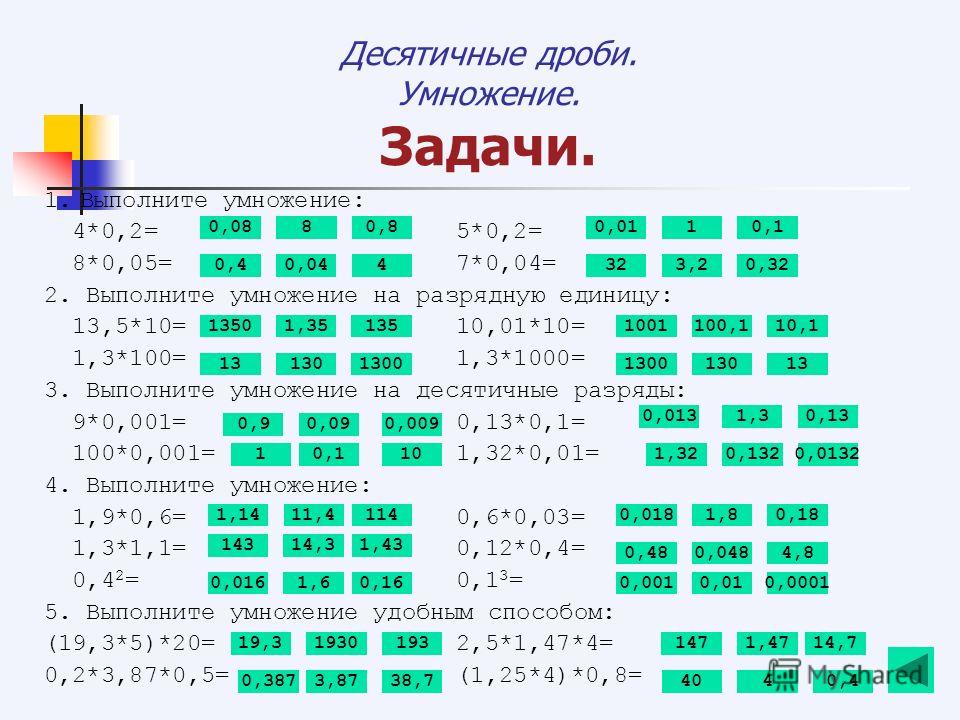
Это полный урок с инструкциями и упражнениями для четвертого класса по умножению на целые десятки и сотни.В уроке объясняется, как работает ярлык, а также объясняется, почему он работает. Он содержит множество упражнений для студентов, в том числе словесную задачу.
1. Умножить.
2. А теперь попробуйте! Умножьте на 20 и 200.
3.Попробуй сам! Заполните.
4. Сарай Марка имеет размеры 20 на 15 футов. Какова его площадь? Напишите число
приговор. А = __________________________________ 5.
Напишите числовое предложение и найдите А = __________________________________ 6.Марку сказали, что ему нужно четыре грузовика гравия, чтобы покрыть подъездную дорожку.
7. Умножить.
8. Умножение.
Напишите числовое предложение для каждого вопроса. 9.В одном часе ______ минут. Сколько минуты в 24 часах? 10. В одном часе ______ минут, а в одном в минуте ______ секунд. Сколько секунд в часе? 11. Эд зарабатывает 30 долларов в час. а. Сколько он будет зарабатывать за 8-часовой рабочий день? г. г. Сколько дней ему нужно будет работать, чтобы заработать больше 1000 долларов? 12. Найдите недостающий фактор. Думайте «задом наперед»! Сколько нулей тебе нужно?
Этот урок взят из книги Марии Миллер «Math Mammoth Multiplication 2», размещенной на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер. | |||
Дж в 7 раз больше, чем 6
Адриан К.
спросил • 04.06.20 Артуро О.
ответил • 06. 06.20
06.20
Опытный учитель физики Репетиторство по физике
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчасВыберите эксперта и познакомьтесь онлайн. Никаких пакетов или подписок, платите только за необходимое время.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А Á Â Ã Ä Å Æ Ç È É Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô х ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊
Умножение 7-значных чисел на 6-значные числа (A)
Добро пожаловать в Рабочий лист по математике умножения 7-значных на 6-значные числа (A) со страницы рабочих листов для длинного умножения на сайте Math-Drills. com. Этот математический лист был создан 2016-08-31 и был просмотрен 10 раз на этой неделе и 31 раз в этом месяце. Его можно распечатать, загрузить или сохранить и использовать в вашем классе, домашней школе или другой образовательной среде, чтобы помочь кому-то выучить математику.
com. Этот математический лист был создан 2016-08-31 и был просмотрен 10 раз на этой неделе и 31 раз в этом месяце. Его можно распечатать, загрузить или сохранить и использовать в вашем классе, домашней школе или другой образовательной среде, чтобы помочь кому-то выучить математику.
Учителя могут использовать рабочие листы по математике в качестве тестов, практических заданий или учебных пособий (например, при групповой работе, на строительных лесах или в учебном центре). Родители могут работать со своими детьми, чтобы дать им дополнительную практику, помочь им освоить новые математические навыки или сохранить свои навыки свежими во время школьных каникул. Студенты могут использовать рабочие листы по математике для овладения математическими навыками на практике, в учебной группе или для взаимного обучения.
Используйте кнопки ниже, чтобы распечатать, открыть или загрузить PDF-версию таблицы «Умножение 7-значных чисел на 6-значные числа» (A) . Размер файла PDF составляет 25099 байт. Показаны изображения для предварительного просмотра первой и второй (если есть одна) страниц. Если существует больше версий этого рабочего листа, другие версии будут доступны под изображениями для предварительного просмотра.Для более того, используйте строку поиска для поиска некоторых или всех этих ключевых слов: math, multiplication, long, multiply, product, 7-значный, 6-значный .
Размер файла PDF составляет 25099 байт. Показаны изображения для предварительного просмотра первой и второй (если есть одна) страниц. Если существует больше версий этого рабочего листа, другие версии будут доступны под изображениями для предварительного просмотра.Для более того, используйте строку поиска для поиска некоторых или всех этих ключевых слов: math, multiplication, long, multiply, product, 7-значный, 6-значный .
Кнопка Печать запускает диалоговое окно печати вашего браузера. Кнопка Открыть откроет весь PDF-файл в новой вкладке вашего браузера. Кнопка Teacher инициирует загрузку полного файла PDF, включая вопросы и ответы (если таковые имеются). Если присутствует кнопка Student , будет инициирована загрузка только страниц с вопросами.Дополнительные параметры могут быть доступны, щелкнув кнопку правой кнопкой мыши (или удерживая нажатой кнопку на сенсорном экране). Я не вижу кнопок!
Умножение 7-значных на 6-значные числа (A) Рабочий лист по математике, страница 1 Умножение 7-значного числа на 6-значные числа (A) Рабочий лист по математике, страница 2Другие версии:
Более длинные листы для умножения
Упрощение / Умножение радикалов | Purplemath
Purplemath
При упрощении у вас не всегда будут только числа внутри радикала; вам также придется работать с переменными. Переменные в аргументе радикала упрощаются так же, как и обычные числа. Вы учитываете вещи, и все, что у вас есть, можно вынести «вперед».
Переменные в аргументе радикала упрощаются так же, как и обычные числа. Вы учитываете вещи, и все, что у вас есть, можно вынести «вперед».
Упростить
Я уже знаю, что 16 — это 4 2 , поэтому я знаю, что выберу 4 из радикала. Затем, глядя на переменную часть, я вижу, что у меня есть две пары x , поэтому я могу вынуть по одной x из каждой пары.Тогда:
MathHelp.com
Как видите, упрощение радикалов, содержащих переменные, работает точно так же, как упрощение радикалов, содержащих только числа. Мы разлагаем на множители, находим квадраты (или, что то же самое, находим факторы, встречающиеся в парах), а затем вытаскиваем одну копию того, что было возведено в квадрат (или того, что мы нашли пару).
Мы разлагаем на множители, находим квадраты (или, что то же самое, находим факторы, встречающиеся в парах), а затем вытаскиваем одну копию того, что было возведено в квадрат (или того, что мы нашли пару).
Упростить
Глядя на числовую часть подкоренного выражения, я вижу, что 12 — это произведение 3 и 4, поэтому у меня есть пара двоек (так что я могу взять 2 впереди), но оставшуюся 3 (которая останется позади внутри радикала).
Глядя на переменную часть, у меня есть две пары и ; У меня есть три пары b , одна b осталась; и у меня есть одна пара c , еще одна c осталась. Таким образом, корень упрощается как:
Вы привыкли ставить сначала числа в алгебраическом выражении, а затем любые переменные. Но для радикальных выражений любые переменные вне радикала должны идти перед радикалом, как показано выше. Всегда помещайте все , которые вы извлекаете из радикала , перед этим радикалом (если что-то осталось внутри).
Всегда помещайте все , которые вы извлекаете из радикала , перед этим радикалом (если что-то осталось внутри).
Упростить
Записывать полную факторизацию было бы утомительно, поэтому я просто воспользуюсь тем, что знаю о полномочиях. 20 множителей равны 4 × 5, причем 4 — это полный квадрат. r 18 имеет девять пар r ; s непарный; и t 21 имеет десять пар t , и одна t осталась.Тогда:
Технический момент: ваш учебник может посоветовать вам «предполагать, что все переменные положительны» при упрощении. Почему? Потому что квадратный корень из квадрата отрицательного числа равен , а не исходному числу.
Например, вы можете начать с –2, возвести его в квадрат, чтобы получить +4, а затем извлечь квадратный корень из +4 (который равен , определяемому как как положительный корень из ), чтобы получить +2. Вы подключили отрицательный результат, а в итоге получили положительный результат.
Вы подключили отрицательный результат, а в итоге получили положительный результат.
Мы применяем процесс, в результате которого мы получаем одно и то же числовое значение, но оно всегда положительное (или, по крайней мере, неотрицательное). Звучит знакомо? Должно: так работает абсолютное значение: | –2 | = +2. Извлечение квадратного корня из квадрата фактически является техническим определением абсолютной величины.
Но эта техническая особенность может вызвать трудности, если вы работаете со значениями неизвестного знака; то есть с переменными.| –2 | +2, но какой знак | x |? Вы не можете знать, потому что вы не знаете самого знака x — если они не указывают, что вы должны «предполагать, что все переменные положительные» или, по крайней мере, неотрицательные (что означает «положительный или ноль»).
Умножение Квадратные корни
Первое, что вы научитесь делать с квадратными корнями, — это «упрощать» термины, которые складывают или умножают корни.
Упростить умноженные радикалы довольно просто и мало чем отличается от уже сделанных нами упрощений. Мы используем тот факт, что продукт двух радикалов совпадает с радикалом продукта, и наоборот.
Запишите как произведение двух радикалов:
Поскольку 6 множителей равны 2 × 3, я могу разделить этот радикал на произведение двух радикалов, используя факторизацию.(Да, я мог бы также разложить на множители как 1 × 6, но они, вероятно, ожидают разложения на простые множители.)
Да, эта манипуляция была довольно упрощенной и не очень полезной, но она показывает, как мы можем манипулировать радикалами. И использование этой манипуляции для работы в другом направлении может оказаться весьма полезным. Например:
Упростите, написав не более одного радикала:
При умножении радикалов, как в этом упражнении, обычно не ставят символ «умножение» между радикалами. Умножение понимается как «сопоставление», так что технически больше ничего не требуется.
Умножение понимается как «сопоставление», так что технически больше ничего не требуется.
Чтобы сделать это упрощение, я сначала умножу два радикала вместе. Это даст мне 2 × 8 = 16 внутри радикала, который, как я знаю, является полным квадратом.
Между прочим, я мог бы сначала упростить каждый радикал, затем умножить, а затем сделать еще одно упрощение.Работа была бы немного дольше, но результат был бы тот же:
sqrt [2] × sqrt [8] = sqrt [2] × sqrt [4] sqrt [2]
= sqrt [2] × 2 sqrt [2]
= 2 × sqrt [2] sqrt [2]
= 2 и умножить на 2 = 4
Упростите, написав не более одного радикала:
Ни один из радикалов, которые они мне дали, не содержит квадратов, так что я не могу ничего вынести вперед — пока.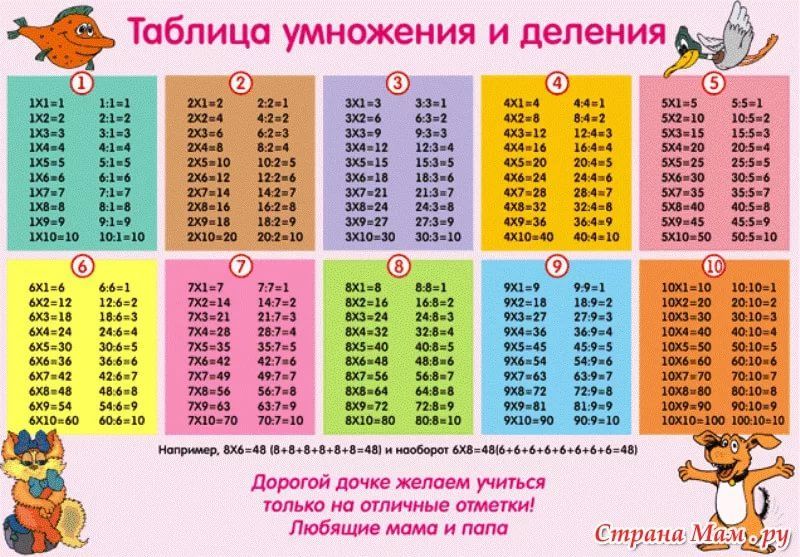 Что произойдет, если я умножу их вместе?
Что произойдет, если я умножу их вместе?
Упростите, написав не более одного радикала:
В таком виде радикалов ничего не упрощается. Однако, как только я умножу их вместе в один радикал, я получу то, что смогу вынуть, потому что:
6 × 15 × 10 = 2 × 3 × 5 × 2 × 5
= 2 × 3 × 2 × 5 × 5 × 3
Итак, я смогу взять 2, 3 и 5:
Процесс работает таким же образом, когда включены переменные:
Упростите, написав не более одного радикала:
Четверка в первом корне — это квадрат, поэтому я смогу извлечь квадратный корень 2 спереди; Я застряну с 5 внутри радикала. Умножив переменные части двух радикалов вместе, я получу x 4 , что является квадратом x 2 , поэтому я смогу взять x 2 спереди. , тоже.
Умножив переменные части двух радикалов вместе, я получу x 4 , что является квадратом x 2 , поэтому я смогу взять x 2 спереди. , тоже.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении произведений радикалов. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
/ p>(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/radicals2.htm
Что такое длинное умножение? — Определение, факты и примеры
Длинное умножение Длинное умножение — это метод умножения двух чисел, которые сложно перемножить.
Например, мы можем легко найти произведение 55 × 20, умножив 55 на 2, а затем добавив 0 в самом правом месте ответа.
55 × 2 = 110 и 55 × 20 = 1100.
Но зачастую найти продукт не так просто. В такие моменты мы используем длинный метод умножения.
Шаги для умножения с использованием длинного умноженияУмножение 2-значных чисел на 2-значные числа
Умножим 47 на 63, используя метод длинного умножения.
1. Напишите два числа одно под другим в соответствии с местами их цифр. Напишите большее число сверху и знак умножения слева. Нарисуйте линию под числами.
2. Умножьте единичную цифру верхнего числа на единичную цифру нижнего числа.
Напишите продукт, как показано.
3. Умножьте цифру десятков верхнего числа на цифру единиц нижнего числа.
Это наш первый частичный продукт, который мы получили, умножив верхнее число на единичную цифру нижнего числа.
4. Напишите 0 под цифрой единиц, как показано. Это потому, что теперь мы будем умножать цифры верхнего числа на цифру десятков нижнего числа. Следовательно, мы пишем 0 вместо единиц.
5. Умножьте цифру единиц верхнего числа на цифру десятков нижнего числа.
6. Умножьте цифру десятков верхнего числа на разряд десятков нижнего числа.
Это второй частичный продукт, полученный при умножении верхнего числа на разряд десятков нижнего числа.
7. Добавьте два неполных продукта.
В методе длинного умножения число наверху называется множимым. Число, на которое оно умножается, то есть нижнее число, называется множителем.
Итак, в задаче с длинным делением будет:
Мы используем тот же метод для умножения чисел, превышающих 2-значные.
На рисунке ниже показан метод длинного деления для умножения 357 на 23
Интересный факт:
|


 1000 × 250 = _______
1000 × 250 = _______
 200 × 25
200 × 25
 200 × 12 = ______
200 × 12 = ______ 20 × 90 = _________
20 × 90 = _________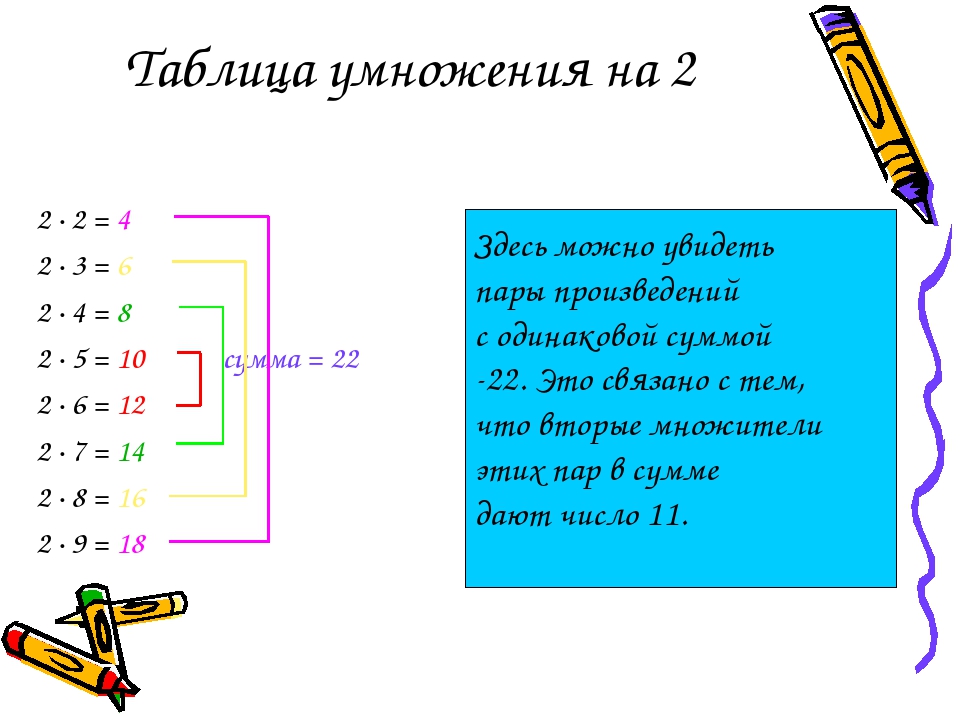 Сколько он будет зарабатывать за 40-часовую рабочую неделю?
Сколько он будет зарабатывать за 40-часовую рабочую неделю? разбивая умножение на более мелкие части.Он написал 40 как
разбивая умножение на более мелкие части.Он написал 40 как