Тригонометрические выражения онлайн калькулятор: Тригонометрический калькулятор | Microsoft Math Solver

Триг-Калькулятор — Mathcracker.Com

Инструкции: Используйте тригонометрический калькулятор для вычисления и оценки любого тригонометрического выражения, которое вы предоставите. Пожалуйста, введите тригонометрическое выражение, которое вы хотите вычислить, или тригонометрическую функцию, которую вы хотите проанализировать, в поле формы ниже.

Подробнее об этом триг-калькуляторе

Этот триггерный калькулятор позволит вам оценить любое тригонометрическое выражение, которое вы предоставите. Убедитесь, что вы предоставили любое допустимое тригонометрическое выражение, это может быть что-то прямое, например cos(pi/2), или что-то не полностью упрощенное, например sin(1/3*pi+3/4*pi).

Вы также можете задать триггерную функцию типа sin(1/3*pi x +3/4*pi + x), и калькулятор проанализирует и, если возможно, выдаст соответствующий период, частоту и т.д., вместе с его график .

После ввода правильного тригонометрического выражения достаточно нажать кнопку «Вычислить», и все этапы вычисления будут показаны.

тригонометрические выражения весьма необходимы, особенно когда вы решение треугольников .

Обычно любой тригонометрический расчет просто свести к вычислению нескольких заметных углов для косинус и синус .

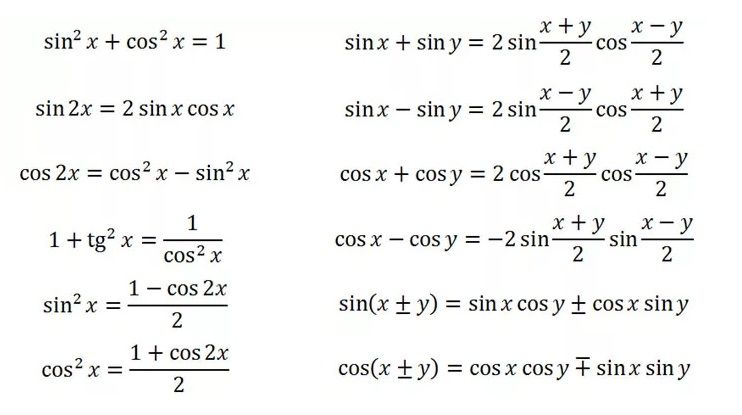
Как выполнять тригонометрические расчеты?

Вычисление тригонометрии может быть очень общей и широкой задачей, которая может иметь конкретные стратегии, которые работают лучше всего в зависимости от конкретного тригонометрического вычисления, которое вам нужно сделать, и от того, какие тригонометрические функции задействованы, но есть некоторые общие стратегии, которые могут послужить вам хорошую службу.

Каковы этапы вычисления тригонометрии

• Шаг 1: Четко определите тригонометрическое выражение, которое вы хотите вычислить, и упростите числа и дроби настолько, насколько это возможно. Например, если у вас есть cos(1+1/2), вы сначала заметите, что 1+1/2 = 3/2, поэтому вам нужно фактически cos(3/2)
• Шаг 2: После того как возможные дроби и простые числа сгруппированы и, по возможности, оперируют ими, определите, существуют ли триггерные функции, отличные от синуса и косинуса. Если они есть, выразите все в терминах синуса и косинуса
• Шаг 3: Теперь пройдитесь по всем частям, которые теперь включают только синус и косинус , и оценить, есть ли заметные углы, кратные или дольные π
• Шаг 4: Непосредственно оцените эти выражения с помощью заметных углы которые можно упростить. Те, которые не могут быть упрощены напрямую (если таковые имеются), оставляют как есть, или дают приближенное ( округлённое значение ) из них

Принято оставлять их такими, какие они есть выражения которые не имеют известных простых упрощений. Например, cos(1/4) не имеет простого сокращения, поэтому его обычно оставляют как есть. Но, например, cos(π/3) = 1/2, поэтому такие простые редукции, очевидно, выполняются

Тригонометрический калькулятор с шагами

Преимущество этот калькулятор заключается в том, что он покажет вам все соответствующие этапы процесса. Процесс прост: он заключается в следующем упрощение выражений в которых используются только числа, дроби и общие числовые выражения с прямой оценкой.

Затем, и только затем вы должны приступить к вычислению тригонометрии, чтобы максимально прояснить ситуацию, прежде чем приступать к вычислению тригонометрии.

Преимущества использования приложения тригонометрического калькулятора

Вы можете подумать: о, хорошо, я довольно хорошо знаю свои триггерные функции для основных заметных углов, поэтому мне не нужно приложение триггерного калькулятора. Это вполне может быть так, хотя вы можете немного колебаться, когда вам предложат что-то вроде \(\sin\left(\displaystyle\frac{345}{11}\pi\right)\).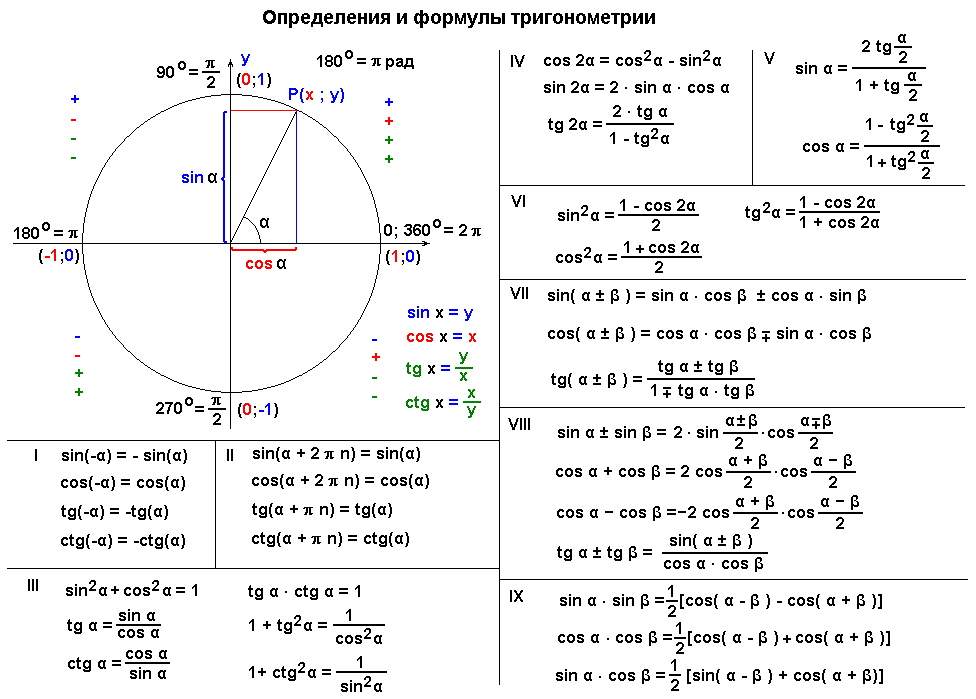 … Можете ли вы упростить это? Является ли это заметным углом?

Это действительно хорошо — пытаться решать задачи вручную, тренируя свою тригонометрическую память, но приложение триггерного калькулятора может помочь вам, по крайней мере, проверить свои ответы.

Пример: вычисление тригонометрии

Вычислите триггерное выражение: \(\sin\left(\frac{5}{4}\pi\right)\)

Отвечать: Необходимо вычислить следующее тригонометрическое выражение:

\[ \sin\left(\frac{5\pi}{4}\right)\]

Рассматривая данное тригонометрическое выражение, мы можем найти один примечательный угол, который равен \(\sin\left(\frac{5\pi{}}{4}\right)\).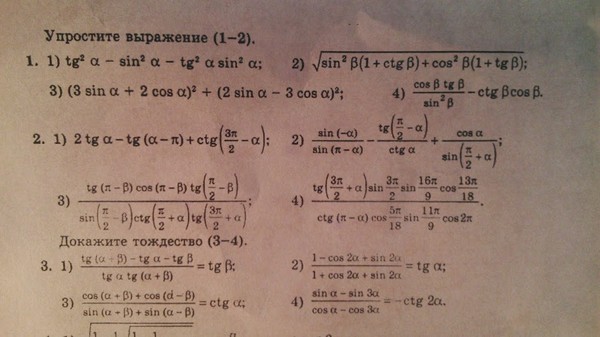

▹ Для угла \(\frac{5\pi{}}{4}\) графически получаем:

Приведенное тригонометрическое выражение может быть упрощено как:

\( \displaystyle \sin\left(\frac{5\pi{}}{4}\right)\)

Evaluating the trigonometric expression at the notable angle \(\displaystyle\frac{5\pi{}}{4}\) we get that: \(\displaystyle \sin\left(\frac{5\pi{}}{4}\right) = -\frac{ \sqrt{2}}{ 2}\)

\( = \,\,\)

\(\displaystyle -\frac{ \sqrt{2}}{ 2}\)

Заключение: Мы заключаем, что \(\displaystyle \sin\left(\frac{5\pi}{4}\right) = -\frac{1}{2}\sqrt{2} \approx -0.7071\).

Пример: использование триггерного калькулятора

Уменьшить : \(\displaystyle \cos\left(\frac{1}{3} + \frac{5}{4}\right)\)

Отвечать: Теперь нам нужно работать дальше:

\[ \cos\left(\frac{1}{3}+\frac{5}{4}\right)\]

Этот тригонометрический член может быть упрощен следующим образом:

\( \displaystyle \cos\left(\frac{1}{3}+\frac{5}{4}\right)\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 1}{ 3}+\frac{ 5}{ 4}=\frac{ 1}{ 3} \times \frac{ 4}{ 4}+\frac{ 5}{ 4} \times \frac{ 3}{ 3}=\frac{ 4+5 \times 3}{ 12}=\frac{ 4+15}{ 12}=\frac{ 19}{ 12}\)

\( = \,\,\)

\(\displaystyle \cos\left(\frac{19}{12}\right)\)

Заключение: Сделан вывод, что \(\displaystyle \cos\left(\frac{1}{3}+\frac{5}{4}\right) = \cos\left(\frac{19}{12}\right) \approx -0.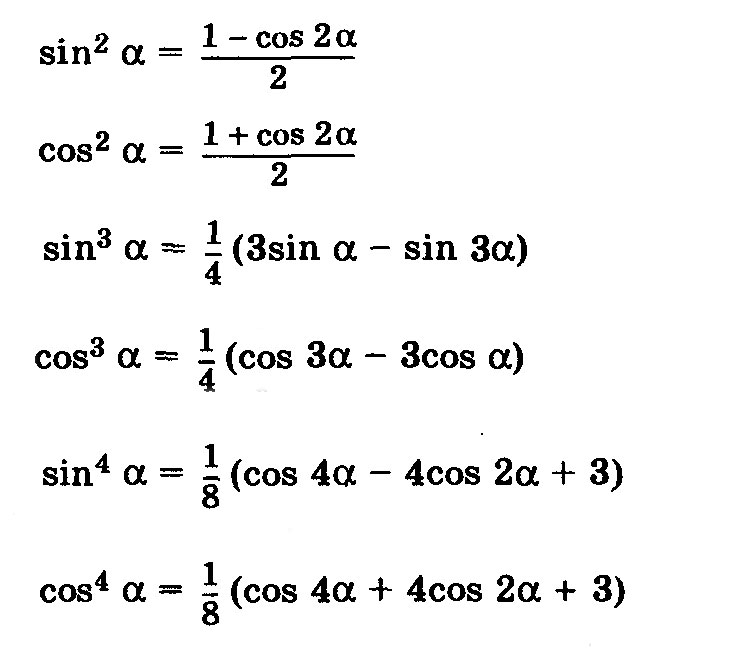 0125\).

Пример: упрощение тригонометрии

Рассчитайте \( \sin\left(\frac{2}{3} \times \frac{6}{5} \pi\right)+ \frac{2}{5}\cdot \cos(\frac{\pi}{4}) \).

Отвечать: Рассматривая данное тригонометрическое выражение, мы можем найти один примечательный угол, который равен \(\cos\left(\frac{\pi{}}{4}\right)\).

▹ Для угла \(\frac{\pi{}}{4}\) графически получаем:

Приведенное тригонометрическое выражение может быть упрощено как:

\( \displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi{}\right)+\frac{2}{5}\cos\left(\frac{\pi{}}{4}\right)\)

Evaluating the trigonometric expression at the notable angle \(\displaystyle\frac{\pi{}}{4}\) we get that: \(\displaystyle \cos\left(\frac{\pi{}}{4}\right) = \frac{1}{2}\sqrt{2}\)

\( = \,\,\)

\(\displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi{}\right)+\frac{2}{5}\cdot\frac{1}{2}\sqrt{2}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 2}{ 3} \times \frac{ 6}{ 5}=\frac{ 2 \times 6}{ 3 \times 5}=\frac{ 2 \times (\cancel{3} \times 2)}{ \cancel{3} \times 5}=\frac{ 2 \times 2}{ 5}=\frac{ 4}{ 5}\)

\( = \,\,\)

\(\displaystyle \sin\left(\frac{4}{5}\pi{}\right)+\frac{2}{5}\cdot\frac{1}{2}\sqrt{2}\)

Evaluating the trigonometric expression at the notable angle \(\displaystyle\frac{4}{5}\pi{}\) we get that: \(\displaystyle \sin\left(\frac{4}{5}\pi{}\right) = \frac{1}{4}\sqrt{-2\sqrt{5}+10}\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}\sqrt{-2\sqrt{5}+10}+\frac{\frac{2}{5}\cdot1}{2}\sqrt{2}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 2}{ 5} \times \frac{ 1}{ 2}=\frac{ 2}{ 5 \times 2}=\frac{ \cancel{2}}{ 5 \times \cancel{2}}=\frac{ 1}{ 5}\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}\sqrt{-2\sqrt{5}+10}+\frac{1}{5}\sqrt{2}\)

Заключение: Мы заключаем, что \(\displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi\right)+\frac{2}{5}\cos\left(\frac{\pi}{4}\right) = \frac{1}{5}\sqrt{2}+\frac{1}{4}\sqrt{-2\sqrt{5}+10} \approx 0. 8706\).

Больше калькуляторов по геометрии

Работа с триггерными функциями тесно связана с работой с треугольниками, поэтому при работе с калькулятор треугольника вы найдете множество триггерных расчетов.

Решение тригонометрических функций ⋆ Компьютерные технологии

Домой Калькулятор онлайн Решение тригонометрических функций

Онлайн калькулятор на нашем сайте легко и быстро решает тригонометрические функции, вам не понадобится таблица тригонометрических функций. С нашим калькулятором можно навсегда забыть, что такое таблица Брадиса! Наш бесплатный калькулятор позволяет решать и самые простые задачи (например, найти косинус или синус угла), и сложные выражения с использованием обратных и гиперболических функций тригонометрии.

Кнопки калькулятора для решения тригонометрических функций:

Наш тригонометрический калькулятор может осуществлять вычисления как в градусах, так и в радианах. Таким образом, найти косинус угла можно вне зависимости от единицы измерения, в которой он задан. Это очень удобно и экономит массу времени при емких расчетах. Прежде чем приступить к вычислениям, нужно на панели управления указать, какая единица измерения углов будет использоваться: градусы (Deg) или радианы (Rad).

Выбор единицы измерения угла:

Обратите внимание, что в одной операции нельзя использовать разные единицы измерения углов, другими словами выражение «сумма синус 30 градусов и косинус пи =» — будет посчитано неверно!

Ниже перечислены способы решений различных тригонометрических функций в нашем онлайн калькуляторе.

Простые тригонометрические функции

Простые тригонометрические функции: синус — sin(α), косинус — cos(β) и тангенс — tan(y). Рядом указаны их обозначения так, как они используются в калькуляторе (в зарубежной литературе тангенс сокращенно обозначается tan, в русской — tg).

Кнопки калькулятора, отвечающие за простые тригонометрические функции:

Функция косинуса является четной, поэтому ее значение для отрицательного угла будет положительным. Синус, тангенс и котангенс — нечетные тригонометрические функции, соответственно, значения тригонометрических функции для отрицательных углов также будут отрицательными. Онлайн калькулятор сам учитывает четность тригонометрических функций при умножении и делении. Вам не потребуется постоянно обращать внимание на соблюдение правила знаков.

Пример вычислений с простыми тригонометрическими функциями:

Обратные тригонометрические функции

Обратные тригонометрические функции: арксинус — asin(), арккосинус — acos() и арктангенс — atan().

Кнопки калькулятора, отвечающие за обратные тригонометрические функции:

Если не вдаваться в формулы и подробности относительно единичной окружности, то обратные тригонометрические функции можно объяснить на простом примере: арккосинус x — это угол, косинус которого равен x. Обратные тригонометрические функции являются многозначными, и одному значению аргумента принадлежит множество значений самой функции.

Пример выражения с обратными тригонометрическими функциями:

Гиперболические функции

Гиперболические функции: гиперболический синус — sinh(), гиперболический косинус — cosh() и гиперболический тангенс tanh(). Гиперболические (круговые) функции — семейство элементарных тригонометрических функций, выраженных через экспоненту.

Кнопки калькулятора, отвечающие за гиперболические функции:

Пример решения гиперболической функции:

Обратные гиперболические функции: гиперболический арксинус — asinh(), гиперболический арккосинус — acosh() и гиперболический арктангенс — atanh().

Кнопки калькулятора, отвечающие за обратные гиперболические функции:

Пример решения обратной гиперболической функции:

Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>

ЭТО ИНТЕРЕСНО

ЭТО ПОПУЛЯРНО

Упростить тригонометрическое выражение — Онлайн калькулятор тригонометрии

Упрощение триггера, онлайн-исчисление

Резюме:

Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.

simple_trig онлайн

---

Описание :

Этот калькулятор позволяет с помощью различных тригонометрических формул от до вычислить тригонометрическое выражение . Тригнометрические выражения — это выражения, включающие функции синуса, косинуса, функции тангенса…

Для упрощения тригонометрических выражений калькулятор использует различные формулы тригонометрии, вот несколько примеров формул тригонометрические, используемые калькулятором:

`AA x в RR, k в ZZ`,

• `sin(-x)= -sin(x)`
• `sin(x+2*k*pi)=sin(x)`
• `sin(pi-x)=sin(x)`
• `sin(pi+x)=-sin(x)`
• `sin(pi/2-x)=cos(x)`
• `sin(pi/2+x)=cos(x)`

• `cos(-x)= cos(x)`
• `cos(x+2*k*pi)=cos(x)`
• `cos(pi-x)=-cos(x)`
• `cos(pi+x)=-cos(x) `
• `cos(pi/2-x)=sin(x)`
• `cos(pi/2+x)=-sin(x)`

• `tan(-x)= -tan( x)`
• `tan(x+k*pi)=tan(x)`
• `tan(pi-x)=-tan(x)`
• `tan(pi+x)=tan(x) `
• `tan(pi/2-x)=1/tan(x)`
• `tan(pi/2+x)=-1/tan(x)`

Это лишь небольшой пример из многих тригонометрических формул, используемых этим тригонометрическим калькулятором.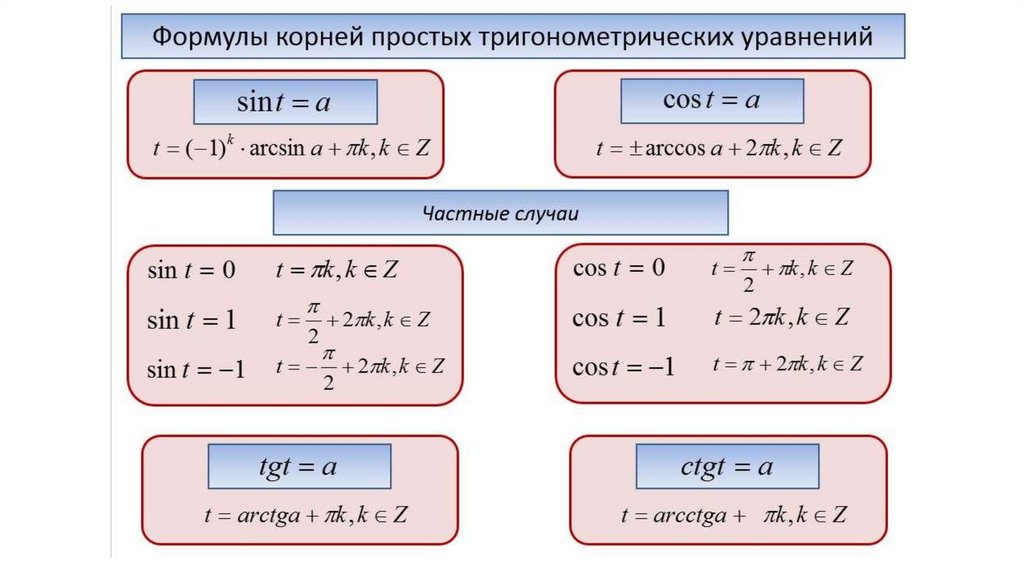

Когда калькулятор упрощает тригонометрическое выражение, он указывает формулы, используемые для получения результата, в разделе, предназначенном для деталей расчетов.

Чтобы упростить тригонометрическое выражение , введите выражение для упрощения и примените функцию simple_trig. Таким образом, для упрощения следующего выражения `cos(x+pi)+2*sin(x)` введите simple_trig(`cos(x+pi)+2*sin(x)`) , после вычисления возвращается упрощенная форма тригонометрического выражения.

В этом другом примере показано, как вычислить тригонометрическое выражение `cos(pi-x)`: simple_trig(`cos(pi-x)`) .

Тригонометрический калькулятор может упростить не только буквенно-цифровые выражения, но и чисто числовые выражения.

Синтаксис:

simple_trig(выражение), где выражение представляет тригонометрическое выражение, которое нужно упростить.

---

Примеры:

simple_trig(`cos(x+pi)`) возвращает `-cos(x)`

Вычислите онлайн с помощью Simplize_trig (тригонометрический калькулятор)

См. также

Список связанных калькуляторов:

• Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
• Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
• Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
• Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
• Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
• Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
• Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
• Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
• Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
• Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
• Тангенс: тангенс. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

Прочие ресурсы

• Алгебраические вычисления
• Бесплатные онлайн игры для алгебраических вычислений
• Научитесь делать алгебраические вычисления

 

Анализатор тригонометрических выражений — MathCracker.

com

Алгебра Решатели

---

Инструкции: Используйте этот оценщик тригонометрических выражений для вычисления таких выражений, как «sin(pi/4)» или «cos(0)» и т. д., и этот калькулятор покажет вам результат. Ответ будет точным для определенных заметных углов и приблизительным для большинства случаев.

Введите тригонометрическое выражение, которое вы хотите рассчитать (пример: cos(2/3*pi) + sin(1/3 pi) и т. д.)

---

Тригонометрические выражения и функции широко распространены во всех областях математики. Важно знать, как их оценивать, и этот калькулятор поможет вам в этом.

Этот калькулятор поможет вам с простыми тригонометрическими выражениями, такими как «sin(pi/4)» или «cos(0)», и любыми другими простыми тригонометрическими выражениями.

Почему вы используете этот калькулятор, а не любой другой калькулятор?

Что особенного в этом калькуляторе, так это то, что он даст вам точное значение выражения всякий раз, когда он имеет дело с заметными углами. Например, если ввести «sin(pi/4)», этот калькулятор даст вам точный ответ \(\frac{\sqrt 2}{2}\), а не приблизительный «0,707106781», который вы получите от большинства калькуляторов. .

Как построить график тригонометрических функций?

Первым шагом в построении графика тригонометрической функции является понимание того, как вычислять тригонометрические функции. Но, тем не менее, вам, скорее всего, понадобится самописец тригонометрических функций сделать это, чтобы получить правильный график.

Как вычислять общие алгебраические выражения?

Если вместо тригонометрического выражения вы имеете дело с чем-то более общим, используйте это общее вычислитель алгебраических выражений .

Вы также можете проверить больше алгебраические решатели и калькуляторы чтобы найти некоторые, которые могут быть полезны для вас.