Опубликовано Калькулятор дробей онлайн | Сложение, вычитание, умножение, деление
- Подробности
Дробный калькулятор онлайн расчитывает произведение, разность, сумму и частное для двух дробей с выводом подробного решения, которое поволяет понять последовательность выполненния арифметических операций с дробями.
Дано:
Решение:
+−×÷
=
4
при просмотре на смартфоне — поверните экран
Выполнение решения
проверка возможности выполнения решения дробей
1) Перевод смешанных дробей в неправильные дроби
перевод смешанных дробей в неправильные дроби
2) Приведение дробей к общему знаменателю
приведение смешанных дробей к общему знаменателю
3) Выполнение операции с дробями
выполнение арифметической операции
4) Определение наибольшего общего делителя (НОД) числителя и знаменателя дроби
определение наибольшего общего делителя (НОД) числителя и знаменателя
5) Сокращение числителя и знаменателя дроби
сокращение числителя и знаменателя
6) Выделение целой части дроби
выделение целой части
7) Перевод алгебраической дроби в десятичную дробь
перевод алгебраической дроби в десятичную дробь
Помощь на развитие проекта premierdevelopment.
ru
Send mail и мы будем знать, что движемся в правильном направлении.
Спасибо, что не прошели мимо!
I. Порядок действий при расчете калькулятором для дробей онлайн:
- Чтобы выполнить сложение, вычитание, умножение или деление дробей введите в соответствующие поля значения числителя, знаменателя для двух дробей и выберите необходимую арифметическую операцию из выпадающего списка. Если дробь смешанная, то также заполните поле, соответствующее целой части дроби. Если дробь простая, то оставьте поле целой части пустым.
- Чтобы задать отрицательную дробь, поставьте знак минус в целой части дроби.
- В зависимости от задаваемых калькулятору дробей и арифметической операции автоматически выполняется следующая последовательность действий:
- перевод смешанных дробей в неправильные дроби, т.е. избавление от целой части дроби: для обеих дробей целая часть умножается на ее знаменатель и суммируется с ее числителем;
- приведение дробей к общему знаменателю : числитель и знаменатель первой дроби умножается на знаменатель второй дроби, а числитель и знаменатель второй дроби умножается на знаменатель первой дроби;
- выполнение заданной арифметической операции с дробями:
- сложение — сложение числителей дробей,
- вычитание — вычитание из числителя первой числителя второй дроби,
- умножение — умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй,
- деление — умножить числитель первой дроби на знаменатель второй дроби, а знаменатель первой дроби на числитель второй дроби;
- определение наибольшего общего делителя (НОД) числителя и знаменателя дроби;
- сокращение числителя и знаменателя дроби на НОД;
- выделение целой части дроби, если числитель итоговой дроби больше знаменателя.
- перевод итоговой алгебраической дроби в десятичную дробь с округлением до сотых.
II. Для справки:
- сокращение дроби
- — замена дроби другой равной дробью, но с меньшими значением числителя и знаменателя.
Калькулятор дробей онлайн
Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:
+−×÷
=
Просто заполните необходимые поля и получите ответ и подробное решение.
Данный калькулятор может работать как с положительными, так и с отрицательными дробями.
При этом нужно помнить, что:
− ac = a− c = − ac
Всегда нужно использовать только последний вариант.
Сложение дробей
С одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.
Формула
ac + bc = a + bc
Пример
Для примера сложим следующие дроби с равными знаменателями:
27 + 47 = 2 + 47 = 67
С разными знаменателями
При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю. А затем сложить числители.
Формула (универсальная)
ac + bd = a⋅d + b⋅cc⋅d
Пример №1
Для примера сложим следующие дроби с разными знаменателями:
12+13=1⋅32⋅3+1⋅23⋅2=36+26=3+26=56
Пример №2
Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:
12+14=1⋅22⋅2+14=24+14=2+14=34
Этот же пример можно решить и применяя вышеуказанную универсальную формулу:
12+14=1⋅42⋅4+1⋅24⋅2=48+28=4+28=68=34
Обратите внимание, что мы сократили дробь:
68=3 ⋅ 24 ⋅ 2=34
Сложение смешанных чисел
Смешанные числа — это такие числа, у которых есть как дробная часть, так и целая.
Преобразуя в неправильную дробь
Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.
Формула
a bc + d ef = b + a ⋅ cc + e + d ⋅ ff
Пример
Для примера сложим два смешанных числа:
312+123=1+3⋅22+2+1⋅33=72+53=7⋅32⋅3+5⋅23⋅2=216+106=21+106=316=5⋅6+16=5⋅
+ 16=516
Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:
316=5⋅6+16=5⋅66 + 16=516
Складывая целую и дробную части отдельно
Целую и дробную части смешанных чисел можно складывать по отдельности.
Формула
a bc + d ef = (a + d) + (bc + ef)
Пример
Решим предыдущий пример этим способом:
3 12 + 1 23 = (3+1)+(12+23) = 4+1⋅32⋅3+2⋅23⋅2=4+36+46=4+3+46=4+76=4+116 = 516
Вычитание дробей
Вычитание дробей происходит по тем же принципам, что и сложение.
С одинаковыми знаменателями
Формула
ac − bc = a − bc
Пример
Для примера вычтем одну дробь из другой с равными знаменателями:
35−25=3−25=15
С разными знаменателями
Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.
Формула
ac − bd = a⋅d − b⋅cc⋅d
Пример
Для примера вычтем одну дробь из другой, с разными знаменателями:
34−13=3⋅34⋅3−1⋅43⋅4=912−412=9−412=512
Вычитание смешанных чисел
Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.
Формула
a bc − d ef = b + a ⋅ cc − e + d ⋅ ff
Пример
312−123=1+3⋅22−2+1⋅33=72−53=7⋅32⋅3−5⋅23⋅2=216−106=21−106=116=1⋅6+56=1⋅
+ 56=156
Умножение дробей
При умножении дробей неважно одинаковые или разные у них знаменатели.
Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.
Формула
ac ⋅ be = a ⋅ bc ⋅ e
Давайте рассмотрим несколько примеров:
Пример №1
Умножим дроби с одинаковыми знаменателями:
13⋅23=1⋅23⋅3=29
Пример №2
Умножим дроби с разными знаменателями:
13⋅24=1⋅23⋅4=212=1⋅
6⋅
=16
Пример №3
Умножим смешанные числа:
112⋅223=1+1⋅22⋅2+2⋅33=32⋅83=3⋅82⋅3=246=4
Деление дробей
При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели. Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Формула
ac : be = a ⋅ ec ⋅ b
Давайте рассмотрим несколько примеров:
Пример №1
Разделим одну дробь на другую с таким же знаменателем:
23:13=23⋅31=2⋅33⋅1=63=2
Пример №2
Делим дроби с разными знаменателями:
12:23=12⋅32=1⋅32⋅2=34
Пример №3
Деление смешанных чисел:
412:223=1+4⋅22:2+2⋅33=92:83=92⋅38=9⋅32⋅8=2716=1⋅16+1116=1⋅
+ 1116=11116
См.
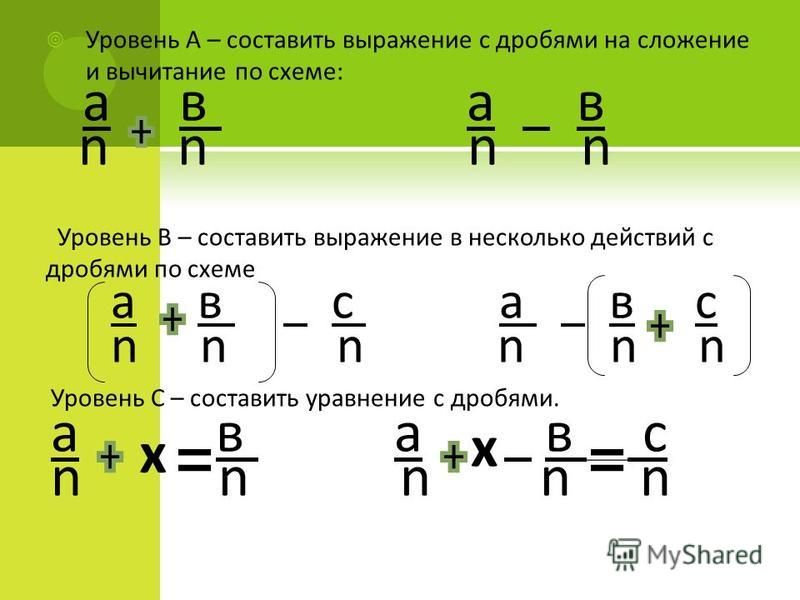
такжеСложение и вычитание дробей с помощью программы «Пошаговое решение математических задач»
С тех пор, как вы начали изучать математику, вы много раз сталкивались с дробями. Они встречаются в формулах и во многих повседневных практических задачах. Однако арифметические дроби состоят строго из чисел. Теперь мы изучим действия над дробями, компоненты которых являются алгебраическими выражениями.
РЕШЕНИЕ УРАВНЕНИЙ, ВКЛЮЧАЮЩИХ ЗНАКОВЫЕ ЧИСЛА
ЗАДАЧИ
По завершении этого раздела вы должны уметь:
- Разложите числитель и знаменатель дроби на множители.
- Упростите алгебраические дроби.
Алгебраическая дробь
При изучении арифметики вам сказали, что дробные ответы всегда следует оставлять в сокращенной или упрощенной форме. Для дроби, до которой вы «уменьшили», разделив числитель и знаменатель на 4. Дробь нельзя уменьшить, потому что никакое число (кроме 1) не будет делить и числитель, и знаменатель.
Упрощая дроби таким образом, вы использовали следующее определение.
Дробь в представляет собой упрощенную (или сокращенную) форму , если числитель и знаменатель не содержат общего множителя (кроме 1).
| Дробь, представленная в упрощенной форме, поскольку числитель 2 и знаменатель 3 не имеют общего делителя, кроме единицы. |
Для получения упрощенной формы дроби применяется следующее правило.
Чтобы упростить дробь
, полностью разложите числитель и знаменатель, а затем разделите числитель и знаменатель на все общие множители.| Дробь , однако, не в упрощенной форме, так как числитель и знаменатель имеют общий делитель 2. |
Затем разделите на общие делители, давая
7 9 деленный делитель само по себе равно 1. |
Теперь разделите на общий множитель (x + 2) как в числителе, так и в знаменателе, чтобы получить
| Мы можем делить только общие множители, но не общие термины. |
| В таком выражении, как у некоторых учащихся, возникает соблазн разделить тройки. Обратите внимание, что это неверное , поскольку они являются терминами , а не факторами. |
Обратите внимание, что даже если мы смогли разложить на множители числитель и знаменатель, мы все равно не можем разделить, поскольку у них нет общих множителей. Данная дробь уже в упрощенном виде.
Тот факт, что для данной дроби может потребоваться любой из изученных вами методов факторинга, еще раз подчеркивает важность владения факторингом.
Решение Здесь вы можете использовать «пробы и ошибки» для числителя и «группировку» для знаменателя.
| Здесь (x + 2) — общий множитель, поэтому можно разделить и числитель, и знаменатель. |
| Обратите внимание, что числитель 2x + 5 можно записать как (2x 4-5) * 1. Таким образом, при делении множителя (2x + 5) остается множитель 1. |
Решение Этот тип проблемы требует особого внимания, так как является частой причиной ошибки. На первый взгляд множители могут быть ошибочно приняты за общие, или дробь может быть ошибочно принята за уже упрощенную. Обратите внимание, что факторы нельзя разделить, поскольку знаки не позволяют им быть идентичными. Если, однако, минус 1 факторизуется от одного из множителей, то есть подобные множители, и деление может быть выполнено.
Любые множители в виде a — b и b — a являются отрицательными значениями друг друга, таким образом, 2x — 3 и 3 — 2x являются отрицательными значениями друг друга. |
| Все это эквивалентные формы одного и того же выражения. Предпочтительной формой будет та, в которой используется наименьшее количество письменных знаков. Всегда проверяйте свой ответ, чтобы убедиться, что он эквивалентен форме, указанной в разделе ответов. |
УМНОЖЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Числители и знаменатели всех умножаемых дробей.
- Определить и разделить на все общие множители.
- Запишите произведение в простейшей форме.
Алгебраическая дробь — это указанное отношение двух алгебраических выражений.
— это определение произведения двух дробей. На словах это означает «умножить числитель на числитель и знаменатель на знаменатель». Вы использовали это правило много раз в арифметике, когда умножали дроби.
Однако помните, что все дробные ответы должны быть в упрощенной форме.
Мы могли бы следовать приведенному выше определению, а затем упростить ответ, как в предыдущем разделе. Но с алгебраическими дробями это может привести к очень сложным выражениям. Следующее правило позволяет нам упрощать по мере умножения, поэтому ответ будет в упрощенной форме.
При умножении алгебраических дробей полностью разложите все числители и знаменатели, затем перед умножением разделите на все множители, общие для числителя и знаменателя.
Произведение остальных множителей числителя будет числителем ответа, а произведение остальных множителей знаменателя будет знаменателем ответа.
| Опять же, помните, что общие факторы должны быть совершенно одинаковыми. |
| Мы будем использовать точку * для обозначения умножения, поскольку использование X можно спутать с переменной x. |
Обратите внимание, что (x + 2) и (2 + x) одинаковы, но (x — 4) и (4 — x) являются отрицательными значениями друг друга. Опять же, есть много возможных форм для окончательных ответов. Приведенная здесь форма предпочтительнее, поскольку она содержит наименьшее количество знаков. |
| В этой проблеме много факторов. Будь осторожен! |
ДЕЛЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Замените задачу на деление связанной с ней задачей на умножение.
- Деление алгебраических дробей.
Деление дробей определяется с помощью умножения.
Чтобы разделить, умножить на величину, обратную делителю.
Чтобы разделить одно алгебраическое выражение на другое инвертировать делитель и изменить операцию на умножение.
| Делитель следует за знаком. Не инвертируйте неправильную дробь. |
Если знаменатель не указан, считается, что он равен 1.
ПОИСК НАИМЕНЬШЕГО ОБЩЕГО ЗНАМЕНАТЕЛЯЦЕЛИПо завершении этого раздела вы должны уметь:
Правило сложения и вычитания дробей требует, чтобы объединяемые дроби имели одинаковый знаменатель. В качестве подготовки к выполнению этих операций мы теперь исследуем метод нахождения наименьшего общего знаменателя для любой группы дробей. общий знаменатель лот двух или более дробей представляет собой выражение, содержащее все множители знаменателя каждой дроби. Наименьший общий знаменатель содержит минимальное количество множителей, чтобы быть общим знаменателем.
Ментальная арифметика позволит вам найти наименьший общий знаменатель для небольших чисел. Если попросить прибавить , то легко получить наименьший общий знаменатель 12. Если спросить, как мы получили 12, мы просто знаем, что 12 — это наименьшее число, которое делится и на 4, и на 6. Однако необходим более сложный метод. если числа больше или если дроби являются алгебраическими дробями. Пример 1 Найдите наименьший общий знаменатель для Решение Если бы у нас не было общего метода, эта задача потребовала бы значительного количества догадок или возможностей проверки.
Рассмотрим определение. Из него мы знаем, что общий знаменатель этих чисел должен содержать все множители каждого из них. Искомое число должно содержать (2)(2)(3), чтобы оно делилось на 12. Оно должно содержать (2)(7), чтобы делиться на 14, и так далее. Действуйте следующим образом:
Предыдущее обсуждение приводит к правилу получения наименьшего общего знаменателя для любого количества дробей, будь то числа или алгебраические выражения. Чтобы найти наименьший общий знаменатель для двух или более дробей:
При проверке второго знаменателя нам нужен дополнительный множитель (x — 2). Наименьший общий знаменатель равен (3x — 4)(2x + l)(x — 2).
Решение ЭКВИВАЛЕНТНЫЕ ДробиЦЕЛИПо завершении этого раздела вы должны уметь:
При дальнейшей подготовке к сложению и вычитанию дробей мы должны иметь возможность заменить данную дробь на дробь с новым знаменателем, не изменяя значение исходной дроби. называется фундаментальным принципом дробей . Анализируя это утверждение, мы видим две эквивалентные дроби и отмечаем, что числитель и знаменатель умножены на одно и то же ненулевое число a. Чтобы заменить дробь эквивалентной дробью , умножьте числитель и знаменатель на одно и то же ненулевое выражение.
Решение Поскольку новый знаменатель находится в факторизованной форме, при проверке мы видим, что первоначальный знаменатель (2x + 3) был умножен на множитель (x — 4). Следовательно, исходный числитель (x + 1) также необходимо умножить на множитель (x — 4), что даст
Решение Поскольку исходный знаменатель (x — 3) был умножен на (2) и (x + 1), исходный числитель (2x + 1) также необходимо умножить на (2) и ( х + 1).
СЛОЖЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙЦЕЛИПо завершении этого раздела вы должны уметь:
Теперь мы готовы складывать алгебраические дроби, используя методы, описанные в двух предыдущих разделах. Следует вспомнить следующее правило из арифметики. Сумма двух или более дробей, имеющих одинаковый знаменатель, равна сумме числителей над их общим знаменателем. Обратите внимание, что это правило допускает только сумму дробей с одинаковым знаменателем. Чтобы сложить две или более дроби, выполните следующие действия:
Этот ответ в сокращенной форме.
Сумма равна
Мы можем использовать меньше письменных шагов, если заметим, что «общий знаменатель» означает, что все дроби имеют один и тот же знаменатель, а если у всех один и тот же знаменатель, то знаменатель необходимо написать только один раз.
ВЫЧИТАНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙЦЕЛИПо завершении этого раздела вы должны уметь:
Вычитание определяется в терминах сложения, поэтому метод вычитания алгебраических дробей будет таким же, как сложение алгебраических дробей, описанный в предыдущем разделе. Вы скоро поймете, почему мы представили их отдельно. Разность любых двух дробей, имеющих один и тот же знаменатель, равна разнице их числителей над их общим знаменателем. Обратите внимание, что это правило совпадает с правилом сложения двух дробей с одинаковым знаменателем. Таким образом, шаги для вычитания дробей такие же, как и для сложения дробей. Чтобы вычесть дроби: Возникает очевидный вопрос: «Если эти две операции одинаковы, зачем изучать их по отдельности?» Ответ заключается в том, что вычитание порождает очень распространенную ошибку, которой ученик должен быть готов избежать.
Упомянутая ошибка часто возникает из-за того, что знак минус влияет на весь числитель второй дроби, а НЕ только на первый член.
Стрелка указывает на ошибку, наиболее часто допускаемую при вычитании дробей. Лучший способ избежать этого — всегда использовать круглые скобки , и вы вряд ли не сможете правильно изменить знак.
СЛОЖНЫЕ ДРОИЦЕЛИПо завершении этого раздела вы должны уметь:
Дроби определяются как указанное частное двух выражений. В этом разделе мы представим метод упрощения дробей, в котором числитель, знаменатель или оба они сами состоят из дробей. Такие дроби называются сложными фракциями . Таким образом, если числитель и знаменатель сложной дроби составлены из простых дробей, ее можно упростить, разделив числитель на знаменатель. Как правило, более эффективный метод упрощения сложной дроби включает использование фундаментального принципа дробей. Умножаем и числитель, и знаменатель на общий знаменатель всех отдельных дробей сложной дроби.
Мы будем использовать фундаментальный принцип, чтобы еще раз упростить LCD 3 и 4 равно 12. Таким образом,
УРАВНЕНИЯ С АЛГЕБРАИЧЕСКИМИ ДРОБЯМИЗАДАЧИПо завершении этого раздела вы сможете:
В главе 2 мы столкнулись с уравнениями, в которых есть дроби. Однако все эти дроби имели числовые знаменатели. Теперь обсудим уравнения, в знаменателях которых есть дроби с переменными. Метод решения этих уравнений будет таким же, как и в главе 2, но есть некоторые дополнительные предостережения, к которым вы должны быть готовы.
Чтобы освежить вашу память, здесь повторяются шаги решения таких уравнений. Основное отличие решения уравнений с арифметическими дробями от уравнений с алгебраическими дробями заключается в проверке. Процесс проверки будет заключаться не только в том, чтобы найти возможную ошибку, но и в том, чтобы определить, есть ли у уравнения ответ. Последняя возможность возникает потому, что алгебраические дроби умножаются на неизвестную величину. Эта неизвестная величина может быть на самом деле равна нулю, что сделает всю работу недействительной.
Поскольку деление на ноль невозможно, мы должны заключить, что x = 1 не является решением. А так как мы не ошиблись в вычислениях, то должны заключить, что это уравнение не имеет решения.
Таким образом, x = -5 является решением. Следовательно, 11 — это сумма, на которую был увеличен числитель. ОБЗОРКлючевые слова
Процедуры
Калькулятор сложения дробейАвтор Wojciech Sas, PhD Отзыв от Bogna Szyk и Jack Bowater Последнее обновление: 29 ноября 2021 г. Содержание:
Этот калькулятор сложения дробей поможет вам оценить сумма до пяти дробей в мгновение ока. Если вы хотите преобразовать дробь в проценты, этот калькулятор может помочь. В приведенной ниже статье вы узнаете не только о том, как складывать дроби, но и о том, как работать с вычитанием. Вы боретесь с , добавляя дроби с разными знаменателями ? Читайте дальше, чтобы никогда больше не сталкиваться с этой проблемой! После того, как вы закончите здесь, сложение фракций больше никогда не будет ужасом! Ознакомьтесь с другими нашими полезными инструментами:
Как складывать дроби? Дробь — это число, образованное из отношения двух чисел ( Оказывается можно любую десятичную дробь преобразовать. В результате вы можете складывать столько десятичных знаков, сколько хотите, рассматривая их как дроби. Всякий раз, когда мы хотим сложить две дроби с общим знаменателем, скажем, Но как сложить дроби с разными знаменателями ? Сложение дробей с разными знаменателями Когда числа имеют разные знаменатели, сложение дробей немного сложнее, так как вы не можете просто складывать числители, как раньше.
|
Другими словами, мы ищем наименьшее число, которое делится на 12, 14, 15 и 18. 
Это наименьший общий знаменатель, поскольку он содержит только те множители, которые необходимы для того, чтобы он делился на 12, 14, 15 и 18.
Другими словами, две или более дроби могут быть сложены только в том случае, если они имеют общий знаменатель. Правило сложения любых двух или более дробей потребует навыков, полученных в двух последних разделах, в дополнение к знанию комбинирования одинаковых терминов.
Чтобы проиллюстрировать это, мы переработаем предыдущий пример.
Если бы они не сокращались, в уравнении было бы член x 2 . Уравнение этого типа (квадратное) будет рассмотрено в главе 11.
Хитрость заключается в использовании общий знаменатель . Давайте посмотрим, как это работает. Let’s say we want to add 
Однако удобно представить результат в его простейшей форме .
И вот он – голод! Что еще хуже, вы только что поняли, что в холодильнике ничего не осталось.